RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 16, ES2003, doi:10.2205/2016ES000567, 2016
A. V. Marchenko1,2, E. G. Morozov3
1The University Center in Svalbard, Longyearbyen, Spitsbergen, Norway
2Also at Department of Civil and Transport Engineering, Trondheim, Norway
3Shirshov Institute of Oceanology, Russian Academy of Sciences, Moscow, Russia
We study seiche oscillations under ice cover in Lake Valunden. The lake is connected to the fjord in Spitsbergen by a narrow (10 m) channel. The length of the lake is 1300 m and its width is 600 m. Mean depth of the lake is 10–11 m. Forcing of seiches in the lake occurs due to the tides. Wind does not have a notable forcing effect. Tidal currents raise and lower the ice cover plate in the lake and the ice cover oscillates with its natural seiche frequencies. Two modes of seiche oscillations exist in the lake. The longitudinal mode has a period of 240–266 s and the transversal mode has a period of 128–145 s.
Seiches are standing waves in enclosed or semi-enclosed water reservoirs. In general, seiches are generated by external forcing mostly by wind and atmospheric pressure variations. The gravity force restores the horizontal surface of water, which is in hydrostatic equilibrium. Pulses of harmonic motion are reflected from the boundaries of the reservoir. Repeated reflections result in standing waves. Oscillation nodes appear at points that experience no vertical motion. The frequencies of seiches depend on the fundamental features of a specific reservoir and do not depend on the mechanism of external forcing. Oscillation frequency (eigen period of seiches) is determined by the geometry and size of the basin, its depth, and configuration of the coastline [Proudman, 1953; Rabinovich, 2009]. Irregularities of the basin geometry do not prevent development of seiches and basins with irregular shapes oscillate with very stable frequencies.
However, the amplitudes of oscillation strongly depend on the intensity of external forcing. Hence, the time variability can be strong. The natural period of a seiche can be estimated from the Merian's formula:
\begin{eqnarray*} T_{\mathrm{seich}} = \frac{2 L}{n \sqrt{g H_{\mathrm{mean}}}} \end{eqnarray*}where $T$ is the period of seiche, $L$ is the length of the basin, $H_{\mathrm{mean}}$ is the average depth of the basin, $g$ is the acceleration due to gravity, and $n$ is the mode number [Merian, 1828]. The seiches occur as natural oscillations in a basin. The mode with the lowest frequency ($n =1$) is referred to as the fundamental mode.
Usually seiches are unnoticeable, except during periods of very smooth water surface. The amplitudes of seiches can be as high as a few centimeters, while their periods are of a few minutes. Seiches can be induced by wind, changes in the atmospheric pressure, tsunamis or tides. In this paper we study the seiches under an ice cover in a lake connected to a fjord in Spitsbergen.
 |
| Figure 1 |
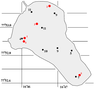
We studied seiches in Lake Valunden, which is located in Spitsbergen. At its northwestern coast the lake is connected with the Van Mijen Fjord by a narrow (10 m) 100 m long channel (Littrowneset) with strong tidal currents [Marchenko et al., 2012]. A chart of the lake is shown in Figure 1. The lake extends from the southeast to the northwest. The lake is approximately 1300 m long and 600–650 m wide. The mean depth of the lake is 10–11 m. Starting from 2008, we made repeated measurements of seiches at different points of the lake in winter and summer using bottom based pressure gauges SBE-39. Seiche oscillations almost always exist in the lake. In March 2015, we used four bottom pressure gauges SBE 39 to measure the pressure variation during six days. The lake and the fjord were covered with ice, but the Littrowneset channel was ice free due to strong tidal currents.
 |
| Table 1 |
In 2015, we made measurements at the points shown in the Table 1 and in Figure 1.
Two spectral peaks usually exist on the spectra of bottom pressure fluctuations in Lake Valunden. The frequencies of peaks are inverse values to periods of 240 and 128 s. These periods correspond to the longitudinal and transversal natural oscillations of the basin. According to the Merian's formula, the periods of spectral peaks correspond to the first modes of seiche oscillations, while the oscillation nodes are located in the middle of the lake.
 |
| Figure 2 |
A typical spectrum of bottom pressure fluctuations is shown in Figure 2. It was calculated from the bottom pressure time series from March 2, 04:00 to 07:00, with a time sampling of 1 s. Two major reliable spectral peaks corresponding to the longitudinal and transversal seiches with periods of 240 s (0.0041667 cps) and 128 s (0.0078125 cps) are seen.
Usually, the seiches appear at strong winds and changes in the atmospheric pressure, and also due to tidal forcing through the Littrowneset channel. If the lake is covered with ice, wind forcing at the surface decreases or even vanishes. In this case, wind forcing is applied to the ice cover plate as a whole. Hence, strong winds do not always induce seiches in the lake. Seiche oscillations in the lake can be generated by the tidal currents through the Littrowneset channel. The depth of the channel is about one meter. Usually, the surface of the channel freezes in winter, and sometimes the channel freezes completely to the bottom. However, in March 2016, the channel was ice free. The tide caused semidiurnal oscillations of the ice cover with an amplitude up to 50 cm.
 |
| Figure 3 |
Observations at point 1 were performed on March 2–3, 2016. Figure 3 shows meteorological conditions during the measurements. Pressure fluctuations at the bottom were caused by tides and seiches. The spectral densities were calculated from time series 3 h long with a time sampling of 1 s. Calculations of spectra were performed with a time shift of each time series equal to 3 h. Thus, each spectrum was calculated from an independent time series of bottom pressure. Time variations in the spectral densities of bottom pressure at inverse frequencies of 240 and 128 s periods are also shown in Figure 3.
The seiche oscillations were intensified at night on March 3. On this day, the wind was also strong, and fluctuations of the atmospheric pressure were recorded, which could have been the causes of intensification of the seiches. However, in the beginning of night on March 2, the wind was even stronger, and the atmospheric pressure decreased rapidly. However, the seiches were not intensified. Hence, strong winds and jumps in the atmospheric pressure do not always lead to intensification of the seiches.
 |
| Figure 4 |
Intensification of seiches in the lake was observed during the period of spring tides on March 9. This time coincided with the new moon and intensification of tide. Figure 4 shows time variations of bottom pressure at point 4. Seiches intensify during the period of low water. This can be seen from the pressure graph. The pressure curve in the figure seems thicker due to the fluctuations related to seiches. We used a band filter to separate the seiches with a period of 266 s. The band-pass of the filter was within 235–278 s. This filtering removes the tidal oscillations. An envelope curve of the fluctuations after filtering is shown in Figure 4. The vertical lines in the figure connect the maxima of longitudinal seiches with the curve of pressure variations. It is seen that seiches intensify during the ebb phase. Thus, tidal oscillation force fluctuations of the ice cover in the lake and as a response to this forcing the ice cover fluctuates with its natural frequencies of seiches.
 |
| Figure 5 |
Figure 5 shows two spectra calculated from the time series on March 10 from 11:30 to 13:30 at points 3 and 5. This is the period of spring tides. Transversal mode at point 5 has a longer period (145 s) than at points 2 and 4 (128 s) because the mean depth in the southeastern part of the lake is shallower, which corresponds to longer periods according to the Merian's formula despite a decrease of the lake width there. Only one peak at a period of 266 s exists at point 3. This point is located at a node of the transversal mode; therefore there is no peak at a period of 128 s.
We calculated the coherence function between the oscillations at points 3 and 5 located at different sides of the lake along its longer axis. Coherence between two time series is a measure of correlation between them. It is determined as
\begin{eqnarray*} \mathrm{Ch} = \sqrt{\frac{Co^2 (\omega) + Q^2(\omega)}{S_1 (\omega) \, S_2(\omega)}} \end{eqnarray*}where $Co$ is the $Co$-spectrum, $Q$ is the quadrature spectrum, and $S_1$ and $S_2$ are the frequency spectra of fluctuations calculated from the two time series [Blackman and Tukey, 1958]. Coherence is a function of frequency and we consider the frequencies of the seiche oscillations. The coherence varies between zero (no correlation) to unity (full correlation). The phase difference between the two time series is determined as
According to the calculations on March 9, coherence between the oscillations at these two points (3 and 5) was 0.98, while the phase difference was 182°.
 |
| Figure 6 |
We calculated the spectra of bottom pressure fluctuations at point 2 and 4 to compare the amplitudes of the transversal mode at the opposite sides of the lake. The amplitudes of the fluctuations with a period of 128 s are almost equal (Figure 6). Coherence between the fluctuations at these two points (2 and 4) was 0.92 [Blackman and Tukey, 1958], while the phase difference was 179°.
We studied seiche oscillations in Lake Valunden, which is covered with ice in winter. It is likely that forcing of seiche oscillations occurs due to the tides. Tidal currents flow into the lake through a narrow (10 m) and shallow (1 m) Littrowneset channel. Tidal currents raise and lower the ice cover plate in the lake and the ice cover oscillates with its natural seiche frequencies. Since the lake has an elongated form, two modes of seiche oscillations existed in the lake. The longitudinal mode has a period of 240–266 s and the transversal mode has a period of 128–145 s.
Blackman, R. B., J. W. Tukey (1958), The Measurement of Power Spectra From the Point of View of Communications Engineering, 190 pp., Dover, New York.
Marchenko, A. V., E. G. Morozov, S. V. Muzylev (2012), A tsunami wave recorded near a glacier front, Natural Hazards and Earth System Sciences, 12, p. 415–419, doi:10.5194/nhess-12-415-2012.
Merian, J. R. (1828), Ueber die Bewegung tropfbarer Flüssigkeiten in Gefässen [On the motion of drippable liquids in containers] (thesis), Schweighauser, Basel (in German).
Proudman, J. (1953), Dynamical Oceanography, 225 pp., Methuen, London (7).
Rabinovich, A. B. (2009), Handbook on Coastal and Ocean Engineering (Ed. Y. C. Kim), Chapter 9, Seiches and harbor oscillations, 193–236 pp., World Scientific Publ., Singapore.
Received 7 July 2016; accepted 11 July 2016; published 14 July 2016.


Citation: Marchenko A. V., E. G. Morozov (2016), Seiche oscillations in Lake Valunden (Spitsbergen), Russ. J. Earth Sci., 16, ES2003, doi:10.2205/2016ES000567.
Copyright 2016 by the Geophysical Center RAS.