
RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 20, ES6005, doi:10.2205/2020ES000718, 2020
\setcounter{page}{0}
P. V. Bogorodskiy1, N. E. Demidov2, K. V. Filchuk1, A. V. Marchenko3,4, E. G. Morozov5, A. L. Nikulina1, A. V. Pnyushkov1,6,7, I. V. Ryzhov1
1Arctic and Antarctic Research Institute, St. Petersburg, Russia
2Vernadsky Institute of Geochemistry and Analytical Chemistry, Moscow, Russia
3University Centre in Svalbard, Longyearbyen, Norway
4Zubov Oceanographic Institute, Moscow, Russia
5Shirshov Institute of Oceanology RAS, Moscow, Russia
6International Arctic Research Center, University of Alaska, Fairbanks, USA
7Global Institution for Collaborative Research and Education} {Hokkaido, , Japan,
The results of ice and hydrological studies of the shallow Bay of Braganzav{å}gen (Van Mayen Fjord Bay, West Spitsbergen Island) in March 2016 and 2018, supplemented with model calculations using a thermodynamic model, are presented. The model uses both known methods of localizing the phase transition region – the classical (frontal) for fast ice and in an extended area (two-phase zone) for bottom sediments. For real atmospheric conditions of winter 2015–2016, the new qualitative features of the process of ice formation in the adjacent layers of sea water and bottom soil are revealed. However, due to insufficient knowledge of the heat and mass transfer properties of bottom sediments, the question of quantitative estimates of the process remains open and can be clarified in special field experiments.
Landfast or immobile ice is an inherent component of the ice landscape developing in the coastal zones of Arctic archipelagos [Cottier et al., 2010; Gerland et al., 2006]. Landfast ice is ordinary congelation ice, however, the features of its formation have a significant impact on the interaction of the sea with the atmosphere and bottom in the shallow coastal zone in winter [Bogorodskii et al., 2010; Khimenkov and Brushkov, 2003; Zhigarev, 1997]. Despite the importance of this problem and its clear engineering application, the current knowledge about interaction processes in these media is rather poor in the Polar regions due to the lack of direct field observations caused by difficulties in conducting instrumental measurements in dynamically active coastal zones.
The primary goal of this study is to collect and analyze data on energy and mass transports in the system of interacting layers of the atmosphere, hydrosphere, and lithosphere in the so-called transition regions [Vasiliev et al., 2011]. These regions include near-shore areas affected by tides, marine accumulation zones, and ground freezing zones, i.e., the regions in which heat transport between the atmosphere and the underlying surface differ significantly from the areas of shallow and deeper shelf. The shallow part of the Van Mijenfjorden (West Spitsbergen Island) was chosen as the primary object of research. In this study we used a numerical model to describe thermodynamic characteristics of the seasonal dynamics of landfast ice and the layer of frozen ground sediments for the interior of the Spitsbergen archipelago.
 |
| Figure 1 |
Expeditionary studies in the Braganzav{å}gen Bay, located in the shallow-water part of the Van Mijenfjorden, were carried out by specialists from the University Center in Svalbard (UNIS) and the Russian Arctic Expedition on the Svalbard archipelago (RAES) in late February–early March 2016 and 2018 (Figure 1). Due to the peculiarities of the hydrological and ice regimes of this bay, its waters have been used as a natural field laboratory of UNIS for sea ice research over the last 15 years [Kowalik et al., 2015; Marchenko and Morozov, 2013; Marchenko et al., 2009, 2011; Shestov et al., 2015; Stoylen and Fer, 2014]. Aksel\oya Island at the mouth of the fjord protects landfast ice from swell waves, prevents its outflow during break-up and limits the advection of warm waters of the Atlantic origin [H\oyland, 2009]. Limited advection of warm waters favors annual freezing in the fjord unlike the neighboring fjords of the archipelago. Several creeks and rivers inflow into the bay. However, despite the influence of the island, warm Atlantic waters penetrate the fjord, forming a cyclonic circulation [Bergh, 2004].
The mean current velocities are oriented to the east near the southern coast of the fjord and to the west near the northern coast. The mean measured current speed is of the order of 0.1 m/s [Bergh, 2004]. Tides have a strong influence on the currents in the Van Mijenfjorden [Shestov et al., 2015]. Maximal measured velocities in the Akselsundet Strait exceed 2.5 m/s [Marchenko and Kowalik, 2017], 0.5–0.7 m/s near the east and west shorelines in the western part of the fjord [Yurik, 1976], and 0.5 m/s at the entrance to the Braganzavägen Bay [Marchenko et al., 2009]. Numerical simulations of tidal dynamics in the Van Mijenfjorden estimated the mean value of current speed due to the tides below 5 cm/s [Shestov et al., 2015].
The ice regime of the Bragantzavägen Bay is mostly governed by large-scale atmospheric processes and differences in the heat content of the sub-ice layer of water due to the interaction of river runoff with Atlantic waters, as well as local topographic factors, which include small ($< 2$ m) bottom depths and semi-enclosed coastal line that affect the nature of tidal phenomena [Marchenko et al., 2009; Shestov et al., 2015].
The Bragantzavägen Bay is confined to the estuary of the valley flooded by the sea and divided into two parts by the multi-arm fore-delta of the Kjellstromelva River (Figure 1b). The coastal zone is represented mainly by abrasive and accumulative shores, corresponding, first of all, to river and glacial valleys. The essential role in the transfer of sedimentary material belongs to the deglational activity of the series of ice mass surrounding the bay, frost weathering, gravitational processes, solifluction, and coastal abrasion. Sediment enters the bay due to fluvioglacial flows, ice factor, and aeolian (aerosol) transport. The bulk of terrigenous material is transported into the bay by rivers and streams of glacial nutrition in the form of suspension which is represented mainly by clay particles. The minor input of siltstones, heterogeneous sand, and fine gravel is also possible [H\oyland, 2009].
Multidisciplinary field studies included the collection of hydrological (measurements of the thermohaline water structure and tidal oscillations), sea ice (measurements of snow depth and sea ice thickness), and geocryological (sampling of bottom sediments) data. Oceanographic observations in the riverbed of the Kjellstromelva River inflowing into the bay from the northeast were carried out at the same points (Figure 1). The riverbed's position was determined by the summer satellite images in the visual range and the location of the tidal cracks in landfast ice in March 2016 and 2018. Oceanographic measurements were made using an XR-620 profiler manufactured by RBR (Canada) and a CTD probe SBE-37SM by Sea-Bird Electronics (USA). Contact measurements of ice thickness and snow depth at the points of temperature and salinity profiling were performed using the Kovacs Ice Thickness Kit tool (USA).
 |
| Figure 2 |
Bottom sediments were sampled across a section through the Kjellstromelva riverbed and in areas of contact of landfast ice with the bottom (ice foot). The sediment samples were taken using a steel pipe of 75 mm in diameter cut off at an angle of 45°. Analysis of the collected sediment cores showed the absence of freezing in the upper layers of sediments in the Kjellstromelva riverbed. Moreover, the samples taken there included clay suspension on the inner walls of the sampler, which prevents a precise determination of the sampling level (Figure 2). However, in the zone of landfast ice bottom outside the riverbed, a core extracted from the bottom sediments was successfully delivered to the RAES chemical analytical Laboratory in Barentsburg. Soil moisture was measured according to the Russian national technical standard GOST 5180-84. The complementary description of the structure and composition of samples was carried out on the basis of visual inspection; a particle size composition was determined manually. For chemical analysis sedimentary permafrost samples were dried and sieved at 1 mm. Afterwards, about 20 g of the dry sediment was suspended in 100 ml deionized water and filtered through 0.45 $\mu$m nylon mesh within 3 min after stirring to estimate the ion content after water extraction.
 |
| Figure 3 |
To describe the freezing of shallow water, we used a version of the one-dimensional thermodynamic model, which simulate a process of phase transitions in a system consisting of two semi-infinite layers of air (subscript "a") and initially thawed saline bottom soil (subscript "th"), separated by a layer of sea water (subscript "w") (Figure 3a, Figure 3b) [Bogorodskii et al., 2018; Vasiliev et al., 1997]. The formation of ice (subscript "i") in the water layer (subscript "w") is described by the classical Stefan problem, taking into account the accumulation of snow (subscript "s"), and freezing of the bottom sediment layer. Phase transition is described by the variant of the model with an extended (two-phase or mushy) area (subscript "m"), the liquid phase in which crystallizes in the temperature spectrum. The layers of ice and sea water are single phase medium: in the ice layer water is absent whereas ice is absent in water and thawed layers. In the mushy zone, the phase composition defined by the thermodynamical equilibrium of ice and an unhardened solution mixture is characterized by the water content $\nu (z,t)$ whose value at the interface can change discontinuously, where $z$ is the downward vertical coordinate, and $t$ is the time.
According to the problem's mathematical statement, the bottom soil has a two-layer structure: mushy (two-phase or partially frozen) zone and thawed layer. It is assumed that the freezing soil is a porous medium saturated only with porous ice and brine. The skeleton of this soil layer (subscript "g") is incompressible and immobile, and all dissolved salt formed during freezing is rejected into the volume of unfrozen liquid. The properties of sea and pore ice are considered the same, and the heat fluxes in all layers of the system are stationary. The conditions of the heat transfer equation are satisfied in the snow and ice layers. In the thawed soil layer the heat and salt transfer equations were modified taking into account the two-phase zone and implemented in the partially frozen layer. The sub-ice water layer where cooling is transferred to the bottom supposed to be homogeneous as the result of convective mixing due to complete salt rejection during the ice formation (considered as if stratification in a shallow basin is absent [Bogorodskii et al., 2010]). All layers of the system except the snow layer are in a state of local thermodynamic equilibrium.
The model is based on the equations of thermal and mass balance during phase transitions. At the upper boundary of the system (subscript "b"), a boundary condition specifies the total heat flux into the atmosphere
\begin{equation} \tag*{(1)} EH = H + LE + R, \quad z = h_{b}, \quad t > 0 \end{equation}where $EH$ is the heat flux through the ice cover; $H$ and $LE$ are the vertical turbulent fluxes of sensible and latent heat, calculated by the integral aerodynamic formulae; $R$ is the long way radiation balance calculated according to Engström linearized formula (shortwave radiation is neglected) [Makshtas, 1984]; $h$ is the layer boundary.
At the surface separating snow and ice (subscript "0"), the conditions for the continuity of the distribution of temperature and heat flux are
\begin{equation} \tag*{(2)} T^{-} = T^{+} \equiv T_{0} , \end{equation} \begin{equation} \tag*{(3)} k_{i} \frac{\partial T^{+} }{\partial z} - k_{s} \frac{\partial T^{-} }{\partial z} =0, \quad z = 0, \quad t > 0 \end{equation}where $k$ is the thermal conductivity; the signs "$-$" and "+" denote the upper and lower sides of the interface.
At the moving surface of the water-ice phase transition (subscript "1") the conditions of the continuity of the temperature distribution, thermodynamic equilibrium (liquidus), and the classical Stefan's condition, the first two are also implemented to the fixed boundary $z =h$.
\begin{equation} \tag*{(4)} T^{-} = T^{+} = T_{eq} -\gamma S\equiv T_{1} , \end{equation} \begin{equation} \tag*{(GrindEQ__5_)} \rho_{i} L \frac{d h_{1} }{d t} = k_{i} \frac{\partial T^{-} }{\partial z}, \quad t>0 \end{equation}where $\gamma$ and $T_{eq}$ are the constants; $S$ is salinity; $\rho$ is the density; $L$ is the latent heat of fusion.
At the lower boundary of two-phase zone (subscript "2") the conditions of the heat balance as well as coupling conditions are satisfied
\begin{equation} \tag*{(6)} m (1-\nu_{2}) \rho_{i} L\frac{d h_{2}}{d t} = k_{m} \left( \frac{\partial T}{\partial z} \right)^{-} - Q, \quad t>0 \end{equation} \begin{eqnarray*} \nu^{-} = \nu_{2} , \quad \nu^{+} = 1, \end{eqnarray*} \begin{equation} \tag*{(7)} T^{-} = T^{+} =T_{eq} -\gamma S\equiv T_{2} , \end{equation}where $k_{m} =(1-m)k_{g} + m\nu k_{w} + m (1-\nu )k_{i}$; $m$ is the porosity; $Q$ is the geothermal heat flux. Diffusion of salt is neglected here.
The initial conditions are assumed to be given:
\begin{eqnarray*} t = 0: \; T(z,0) = T_{0} , \end{eqnarray*} \begin{equation} \tag*{(8)} S(z,0) = S_{0}, \quad z\in [0,h]. \end{equation} \begin{equation} \tag*{(9)} \nu = \nu_{\infty } = 1, \quad h_{1} (0) = 0, \quad h_2 (0) = h, \end{equation} \begin{equation} \tag*{(10)} T = T_{0} , \quad S = S_{0} , \quad z\in [h_{2} ,\infty ) \end{equation}where the subscript "0" indicates the initial time $t=0$.
For calculations, the following parameters were used [Cheverov et al., 2007; Chuvilin et al., 2013; Makshtas, 1984; Nazintsev et al., 2000]: $\rho_{w} = 1000$ kg/m$^{3}$, $\rho_{i} = 910$ kg/m$^{3}$, $\rho_{g} = 2000$ kg/m$^{3}$, $\rho_{a} = 1.3$ kg/m$^{3}$, $k_{w} = 0.58$ W/(m K), $k_{i} = 2.23$ W/(m K), $k_{s} = 0.31$ W/(m K), $k_{g} =2$ W/(m K), $C_{w} =4190$ J/(kg K), $C_{i} =2000$ J/(kg K), $C_{g} =1920$ J/(kg K), $C_{a} =1000$ J/(kg K), $m= 0.35$, $L = 333.7 \times 10^{3} $ J/kg, $\gamma = 0.054$° C/psu, $T_{eq} =0$° C, $Q = 0.06$ W/m$^{2}$. Due to the lack of water content data on the mushy and thawed zones boundary, the value $\nu_{2} $ was chosen of the order of 0.1, which is in good agreement with the laboratory analysis results of the water content of the upper part of the selected bottom sediments core samples.
The model (1)–(10) was integrated over 149 days, from 3 November 2015. The beginning of integration corresponds to a stable transition of air temperatures through the freezing point and was specified using Svalbard ice maps of the Norwegian Meteorological Institute (http://www.npolar.no. The end of simulations corresponds to the significant increase in solar radiation occurred on 20 March 2016. The calculations were performed for the initial salinity of water of 33.5 psu and depths of 0.5, 1, and 3 m, where the under-ice layer maintains its uniformity.
The atmospheric forcing was set up by standard values of the air temperature with 3 hours of time step, measured at the Sveagruva Weather Station, located on the shore of the bay. The cloud cover data were measured at the Barentsburg Weather Station. Due to the unsatisfactory quality of snow accumulation measurements at this station, the snow depth was set by a linear dependence providing 0.2 m of snow at the 149 day from the beginning of ice formation.
 |
| Figure 4 |
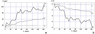
The landfast ice growth at various depths is shown in Figure 4a. The performed calculations showed that ice formation in water layers and sediments starts simultaneously. This finding is in contrast to the conclusions reported in [Khimenkov and Brushkov, 2003], suggesting that the onset of bottom sediments freezing is only possible when the landfast ice reaches the bottom. The pattern of landfast ice growth during the first 40 days for all depths is approximately the same. After 40 days, ice thickness is stabilized in shallow water $h_{i} $ ($h_{i} \equiv h_{1} $), following the decrease in freezing temperature of the sub-ice layer due to salinity increase. The analysis of the calculation shows the effect of water salinization on ice growth, which is traced to a depth of approximately 3 m. With further depth increase, it becomes smaller.
The thickness of the two-phase zone $h_{m} \equiv h_{2} -h$ has an inverse dependence on depth, decreasing as the depth starts to grow (Figure 4b): the following decrease in the temperature of the water layer leads to even stronger freezing of the system. Moreover, for a depth of 1 m, the ice increase in the layers of water and bottom sediments occurs approximately in the same manner. Dependence of landfast ice thickness on depth indicates a bottom depth value of 2 m as a boundary one, the further growth of which makes the effect of salinization (convective cooling mechanism) on ice formation insignificant. At the same time, it should be kept in mind that at a depth less than 0.5 m, the utilized snow accumulation should lead to ice flooding under the weight of the snow and the formation of infiltration ice.
 |
| Figure 5 |
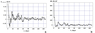
Sub-ice layer salinity (Figure 5a) significantly increases at shallow depths compared to the initial salinity (up to 4 times at a depth of 0.5 m) due to a decrease in the water temperature in a thin sub-ice layer (Figure 5b). Such an increase in salinity allows the sub-ice layer to exist in the liquid phase, despite the significant (up to $- 21$° C) decrease in air temperature. A similar effect of under-ice salinization with extremely high salinity (up to 700 psu) was reproduced by modeling in the shallow part of the Tiksi Bay in the winter of 2014–2015 [Bogorodskii et al., 2018].
 |
| Figure 6 |
Numerical experiments show that landfast ice freezing with the bottom is theoretically excluded due to salinization. Even at the lowest air temperatures the liquid sub-ice layer is not completely frozen out, but remains between ice and bottom in form of thin (several mm) brine layer. As expected, the rate of the phases boundaries $w_{i} = dh_{1} /dt$, $w_{m} = dh_{2} /dt$ for the atmospheric conditions in winter 2015–2016 (Figure 6a) rapidly decreases over time and stabilizes after 60 days, becoming approximately the same, close to 0.02 cm/h. The occasional appearance of negative values of $w_{i}$ and $w_{m}$ (melting ice cover) is explained by a change in the sign of heat flux through the ice (Figure 6b) with increasing air temperature. In general, at the considered shallow depths, the $EH$ values are very close to each other and decrease almost to zero in a week after the start of its formation.
Although the sampled sediment core was completely frozen, the upper 3-cm layer of sediment remained thawed. The visual inspection of the core showed that sediments had a homogeneous, finely-layered fissured structure along the core and contained ice inclusions and saline stains. In general, the sediments could be described as saline and solidly frozen silt sandy loam with reticulate microschlieren cryogenic structure. The gravimetric water content of the sampled sediments was 33% on average. The mineralization of aqueous extract of the sediments calculated after it was measured using Mettler Toledo S320 salinometer did not exceed 3000 mg/l, which indicated low salinization of the frozen bottom sediments. The thermal conductivity coefficient of Braganzav{å}gen's sediments was estimated to be 1.86 W/(m K), while along the coefficient of heat capacity was $2.35 \times 10^{-6}$ J/(m$^{3}$ K). The derived thermodynamic properties are close to those typical for the sediments of the Laptev Sea [Cheverov et al., 2007; Chuvilin et al., 2013]. According to Russian building codes and regulations SNiP II-18-76 "Bases and foundations on permafrost" (http://docs.cntd.ru/document/9056423) on classification of natural deposits and the average natural density of the frozen silty loam sediments was estimated to be approximately 1750 kg/m$^{3}$. However, one should take into account the fact that sampling was conducted under the air temperature about $-10 \ldots -15$° C and samples were further stored at $-20$° C prior to visual examination and analysis, therefore the described properties could undergo slight changes compared to the natural conditions.
Despite the plausibility of model simulations, they should be considered as purely evaluative, characterizing approximate evolution scenarios for the simulated system due to several simplifications. The applied formulation of the problem does not take into account the possible supercooling of pore water within the layer of bottom sediments. The magnitude of supercooling depends on the sediment mineralization (supercooling increases with the growth of mineralization) and is directly proportional to the cooling time. It has been experimentally established that this temperature relationship is linear in the range of freezing temperatures from 0 to $- 1.5$° C, and transforms into a power law if temperature decreases further [Grishin, 1963]. On the other hand, there are data [Khimenkov and Brushkov, 2003] suggesting that when salinization exceeds 5 psu, supercooling of the pore solution often does not occur. The interaction of seawater with bottom sediments leads to salt diffusion and osmosis. The development of these processes can significantly change the amount of pore moisture, its mineralization, ion-salt composition, and, thus, the thermal properties of sediments. As it follows from the previous discussion, the condition of thermodynamic equilibrium in the soil in the form of a linear relationship may not describe all the features of such a complex physical process as freezing of pore moisture in saline sediments.
In addition, it is very likely that horizontal mixing and advection of salt caused by reverse tidal currents, which the utilized one-dimensional model does not reproduce in principle, impede the formation of zones of high salinity due to the advection of fjord freshened waters at the level-raising phase and saline water outflows at the low tide. It should be noted, however, that the average slopes of the bottom, determined from the bathymetric map, are insignificant and can be estimated as about 0.001, which allows us to neglect the gravitationally-driven baroclinic flow from the dense brine (https://toposvalbard.npolar.no/).
 |
| Figure 7 |
The characteristics of tides and their influence on the thermohaline structure of the sub-ice water layer were evaluated based on instrumental measurements of bottom temperature, salinity, and pressure with time resolutions from 1 to 2 minutes. For that purpose, we used the classical method of harmonic analysis [Foreman, 1977]. Unfortunately, the relatively short length of the used records (about 10 days) did not make possible correct spectral resolution between frequencies of different tidal harmonics in the semidiurnal (S2, M2, N2) and diurnal (K1 and O1) tidal constituents. The results of the harmonic analysis performed for the hydrological series with removed linear trends indicate the predominance of tidal signal in the variability of the thermohaline properties in the bottom layer. Hence, for example, at station B2 (see Figure 1), the joint contribution of the distinguished diurnal and semidiurnal tidal harmonics was up to 79% for a series of temperatures and up to 95% for sea level height time series (Figure 7).
An analysis of tidal amplitudes at station B2 in 2018 showed the predominance of the semidiurnal lunar harmonic (the harmonic M2) over other tidal components. The distinguished sea level amplitude was $0.37 \pm 0.2$ m, suggesting a relatively high energy of tidal dynamics in this part of the fjord. Reconstruction of the total tide showed that the contribution of the semidiurnal wave M2 is significant and accounts for about 90%. However, due to the unresolvable spectrum for individual harmonics, we can only conclude about the predominance of the total semidiurnal tide without further separation of its individual components. The harmonics of the diurnal frequency band, as a rule, are significantly (almost one order of magnitude) weaker in the bay and do not exceed 0.05 m at station B2. Temperature observations at this mooring showed that the bottom layer was almost at freezing temperature, and, as a result, tidal changes in the bottom temperature and salinity were not substantial compared to the record variances (less than 0.03° C and 0.4 psu, respectively). It should also be noted that semidiurnal fluctuations in temperature and salinity are out of phase, so that the maximum temperatures, as a rule, correspond to the minimum salinities.
At the same time, the collected near-bottom pressure measurements from a set of moorings deployed in 2016 showed that the amplitudes of tidal level changes are unevenly distributed over the fjord, decreasing as the tidal wave propagates from the seaward southwestern part of the fjord to its shallow northeastern part. This pattern of amplitudes is a typical feature for an induced tidal wave propagating in a semi-enclosed basin of the bay. The evident decrease of tidal amplitudes toward the shallow areas along with their moderate values likely suggests the insignificance of advective transport caused by tidal dynamics there. Thus, we assume that tidal mixing does not restrict the existence of near-bottom zones with high salinity. An indirect confirmation of this assumption can be seen from significant (up to 40‰) growth of water salinity in the bottom layer on the phase of sea level rise, recorded on 15 March 2018 (Figure 7).
Direct instrumental observations in the interacting layers of air, ice, water, and bottom sediments alongside model simulations allowed us to quantify thermodynamic processes in the Bragantzavägen Bay and to describe their qualitative features. The sediments freezing in the transition zone of the bay is determined mainly by its ice regime and, first of all, by the onset of landfast ice formation and the rate of its growth, which, in turn, is formed under the impact of weather and, at longer time scales, climatic changes. Under conditions of limited water exchange between the shallow and deeper parts of the fjord, associated with low intensity of tidal advection, the growth of landfast ice in the shallowest parts of the Braganzav{å}gen Bay has slowed down or even stopped in the middle of winter, while the layer of bottom sediments here freezes most deeply. Ice formation in both layers (in water and ground layers) begins almost simultaneously due to the insignificance of the geothermal heat flux. The presence of a non-freezing layer of brine under the ice theoretically excludes the freezing of the reservoir to the bottom due to the salinization of the ice layer, even at the extremely low air temperatures. The depth of soil freezing is limited by the efficiency of the convective bottom cooling mechanism.
Bergh, J. (2004) , Measured and modelled tidally driven mean circulation under ice cover in Van Mijenfjorden, M.Sc. thesis, Thesis, Department of Oceanography, Göteburg University, Göteburg, Sweden.
Bogorodskii, P. V., A. V. Marchenko, et al. (2010) , Formation of fast ice and its impact on the coastal zone of the Arctic seas, Oceanology, 50, no. 3, p. 345–354, https://doi.org/10.1134/S0001437010030033 (in Russian).
Bogorodskii, P. V., A. S. Grubiy, V. Y. Kustov, et al. (2018) , Growth of the fast ice and its influence on the freezing of bottom sediments in the Buor-Khaya Bay (Laptev Sea) coastal zone, Ice and Snow, 58, no. 2, p. 213–224, https://doi.org/10.15356/2076-6734-2018-2-213-224.
Cheverov, V. G., I. Yu. Vidyapin, V. E. Tumskoj (2007) , The composition and properties of thermokarst lagoons deposits at the Bykovsky Peninsula, Earth Cryosphere, 11, no. 3, p. 44–50.
Chuvilin, E. M., B. A. Buhanov, V. E. Tumskoj, et al. (2013) , Thermal conductivity of bottom sediments in the region of Buor-Haya Bay (shelf of the Laptev Sea), Earth Cryosphere, 17, no. 2, p. 32–40.
Cottier, F. R., F. Nilsen, R. Skogseth, et al. (2010) , Arctic fjords: a review of the oceanographic environment and dominant physical processes, Fjord Systems and Archives, Geological Society Special Publication, J. A. Howe, W. E. N. Austin, M. Forwick, M. Paetzel (Eds.), no. 344, p. 35–50, https://doi.org/10.1144/SP344.4.
Foreman, M. G. G. (1977) , Manual for tidal heights analysis and prediction. Pacific Marine Science Report 77-10, 97 pp., Institute of Ocean Sciences, Patricia Bay, Sidney, BC.
Gerland, S., R. Hall (2006) , Variability of fast ice thickness in Spitsbergen fjords, Ann. Glaciology, 44, p. 231–239, https://doi.org/10.3189/172756406781811367.
Grishin, P. A. (1963) , The freezing temperature of saline soils, The works of the SOYUZMORNIIproekt, 3, no. 9, p. 84–91 (in Russian).
Hoyland, K. (2009) , Ice thickness, growth and salinity in Van Mijenfjorden, Svalbard, Norway, Polar Research, 28, p. 339–352, https://doi.org/10.1111/j.1751-8369.2009.00133.x.
Khimenkov, A. N., A. V. Brushkov (2003) , Oceanic Cryolithogenesis, 336 pp., Nauka, Moscow (in Russian).
Kowalik, Z., A. Marchenko, et al. (2015) , Tidal currents in the western Svalbard Fjords, Oceanologia, 57, p. 318–327, https://doi.org/10.1016/j.oceano.2015.06.003.
Makshtas, A. P. (1984) , Heat Balance of Arctic Ice in the Winter Period, 66 pp., Hydrometeoizdat, Leningrad (in Russian).
Marchenko, A., Z. Kowalik (2017) , Investigation of ocean currents in Navigational Straits of Spitsbergen, Proc. of 12th International Conference on Marine Navigation and Safety of Sea Transportation, TransNav 2017, 21–23 June 2017, p. 267–272, CRC Press, London, https://doi.org/10.1201/9781315099132-33.
Marchenko, A. V., E. G. Morozov (2013) , Asymmetric tide in Lake Vallunden (Spitsbergen), Nonlinear Processes in Geophysics, 20, p. 935–944, https://doi.org/10.5194/npg-20-935-2013.
Marchenko, A., I. Langen, A. Shestov (2009) , Hydrological characteristics of a narrow and shallow part of Van Mijen Fjord on Spitsbergen, Proc. Int. Offshore & Polar Eng. Conf., Osaka, Japan, 21–26 June 2009, p. 649–657, ISOPE, Osaka, Japan.
Marchenko, A., A. Shestov, et al. (2011) , Field studies of sea water and ice properties in Svalbard fjords, Proc. 21th Int. Conf. on Port and Ocean under Arctic Conditions, p. POAC11-148, POAC, Montreal, Canada (ISSN 2077-7841).
Nazintsev, Yu. L., V. V. Panov (2000) , Phase Composition and Thermal Characteristics of the Sea Ice, 83 pp., Leningrad, Gidrometeoizdat (in Russian).
Shestov, A., D. Wrangborg, A. Marchenko (2015) , Hydrology of Braganzav{å}gen under ice-covered conditions, Proc. 23rd Int. Conf. on Port and Ocean Eng. under Arctic Conditions (POAC) June 14–18, 2015 Trondheim, Norway, p. 11, POAC15-00181, Trondheim, Norway.
Stoylen, E., I. Fer (2014) , Tidally induced inertial motion in an Arctic fjord, Nonlinear Processes in Geophysics, 21, p. 87–100, https://doi.org/10.5194/npg-21-87-2014.
Vasiliev, V. I., A. M. Maksimov, et al. (1997) , Heat and Mass Transfer in Freezing and Thawing Grounds, 224 pp., Nauka, Moscow (in Russian).
Vasiliev, A. A., I. D. Streletskaya, et al. (2011) , Coastal permafrost evolution of western Yamal in context of climate change, Earth Cryosphere, XV, no. 2, p. 56–64 (in Russian).
Yurik, Ya. V. (1976) , Main Physical and Mechanical Characteristics of Deposits Properties. Calculation Tables, 216 pp., Budivel'nik Publ., Kiev.
Zhigarev, L. A. (1997) , The Cryolitosperic Zone of Ocean, 320 pp., Publishing of Moscow State University, Moscow (in Russian).
Received 27 April 2020; accepted 26 May 2020; published 9 November 2020.


Citation: Bogorodskiy P. V., N. E. Demidov, K. V. Filchuk, A. V. Marchenko, E. G. Morozov, A. L. Nikulina, A. V. Pnyushkov, I. V. Ryzhov (2020), Growth of landfast ice and its thermal interaction with bottom sediments in the Braganzav\"{a}gen Gulf (West Spitsbergen), Russ. J. Earth Sci., 20, ES6005, doi:10.2205/2020ES000718.
Copyright 2020 by the Geophysical Center RAS.