
RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 20, ES1005, doi:10.2205/2020ES000693, 2020
A. G. Zatsepin, V. V. Kremenetskiy, O. I. Podymov, A. G. Ostrovskii
Shirshov Institute of Oceanology, Russian Academy of Sciences, Moscow, Russia
A possible ventilation mechanism of the aerobic zone in the Black Sea may exist, caused by a descent of oxygen-containing water down the bottom slope in the Ekman boundary layer. To study this theory three long-term (1.5–2 months) installations of automatic bottom stations were carried out in 2018–2019 on the Black Sea shelf/continental slope in the depth range from 80 to 243 m. The stations were placed on a coastal cross section on the beam of the Tolstyi Cape (the Gelendzhik Bay). They recorded the hydrophysical (temperature and salinity of water, pressure and flow rate) and hydrochemical (dissolved oxygen concentration) parameters at 0.5–2.5 m from the bottom. The acquired data were used to estimate the spatiotemporal scales of water transfer in the bottom layer along the slope. Our analysis had confirmed the existence of the bottom water transport normal to the shore. A downward flow was observed in the case of an intensive north-western alongshore current. This type of water movement corresponds to both the geostrophic adjustment and the dynamics of the bottom Ekman boundary layer. However, changes in water density in the bottom layer, which occur due to the water movement up and down the slope, were of the same range as those observed in the water column at the same depth. This fact casts doubt on the efficiency of the Ekman transport in the bottom layer as the ventilation mechanism for water of the upper continental slope of the Black Sea.
Zatsepin et al. [2007] suggested that there is a possible ventilation mechanism for water in the Black Sea pycno-halocline: a descent of oxygen-containing water in the bottom boundary layer (BBL) down the continental slope and its convective mixing with overlying stratified water layers. The details of this process are as follows. When an intense quasi-stationary alongshore current is present and reaches the bottom, the BBL is formed, where the integral Ekman water transport is perpendicular to the current and directed leftward in the northern hemisphere. Influenced by a cyclonic alongshore current, or around-island anticyclonic circulation, water in the BBL is being transported away from the shore and may descend down the continental slope. Such currents are referred to as "downwelling currents", as opposed to upwelling currents, which go in the opposite direction and cause an uprise of water in the bottom Ekman layer [Zhurbas et al., 2006]. Steady density stratification of the marine environment limits the depth of both upwelling and downwelling in the BBL. In case of a downwelling current, water in the BBL, once reaching a certain depth and being lighter than overlying layers, must become affected by convective instability and mix with them. Products of the mixing can penetrate the surrounding stratified water environment in the form of quasi-isopycnic intrusions.
 |
| Figure 1 |
Since the coastal downwelling currents are common in seas and oceans, the described process should be frequent and play a certain role in the ventilation of stratified water columns. Ostrovsky and Zatsepin [2016] suggested that it could be a major factor of oxygen ventilation in the biologically productive layer of the Black Sea, contributing to confining the upper boundary of the anoxic zone below the main pycnocline. There is some evidence confirming that hypothesis. In particular, Figure 1 shows an example of the naturally observed descent of water, rich with chlorophyll-a, from the a depth of 50–60 m to the depth of 90–100 m along the inclined bottom during an intense northwestern current. However, how often this process occurs and how effective it is in the Black Sea and other seas is currently unknown.
There are a whole number of experimental and theoretical studies, starting from the 1970s, that are dedicated to the problems of the BBL existence in the ocean and normal to the shore water transport in that layer [Dickey and Van Leer, 1984; Garrett et al., 1993; MacCready and Rhines, 1993; Perlin et al., 2005, 2007; Pollard et al., 1973; Schaeffer et al., 2013; Weatherly, 1972; Weatherly and Martin, 1978]. One of the conclusions from those works is that there is no BBL model that would sufficiently describe different observations carried out in different areas of the World Ocean and in different hydrophysical conditions. In the Black Sea the BBL was studied the most by V. M. Kushnir, with co-authors (for example, [Kushnir, 2007]). His works demonstrate that the BBL thickness above the continental shelf varies in a wide range: from 5 to 40 m. At the same time a rather high correlation is observed between the thickness of that layer (estimated via changes in density gradient) and current velocity at its upper boundary. The structure of current velocity in the boundary layer is defined by the logarithmic law ("the law of the wall"). However, no reliable evidence was acquired that would confirm a gradual leftward rotation of the velocity vector in the BBL, which in theory should be observed in the northern hemisphere as one gets closer to the bottom. Also, while independence of the BBL thickness from the stratification parameter – the Brunt-Väisälä frequency – seems quite plausible for the weakly stratified zones of the Black Sea (deeper layers below 200 m and the cold intermediate layer (CIL) on the shelf at 40–80 m), it is hardly true for the highly stratified layer of the pycno-halocline, which is the primary study subject of this paper. Another factor, whose influence should affect the BBL structure and dynamics, is bottom inclination. It is clear that all these aspects require additional study.
Pollard et al. [1973] first proposed one of the possible parameterizations of the BBL thickness $H_b$ in the pycnocline on the horizontal bottom for the Ekman surface layer:
\begin{equation} \tag*{(1)} H_b = \frac{K \, U^*}{(N\,f)^{0.5}} \end{equation}where $U^*$ – shear velocity in the BBL, $N$ – the Brunt-Väisälä frequency in the surrounding water environment, $f$ – the Coriolis parameter, $K = 1.4$ – a coefficient.
A dependence, very close to (1) and describing the thickness of the Ekman bottom layer in a stratified ocean, was proposed and experimentally proven by Weatherly and Martin [1978]:
\begin{equation} \tag*{(2)} H_b = \frac{1.3 \, U^*}{f\, (1+ N^2/f^2)^{0.25}} \end{equation}It follows from (2) that without stratification $H_b$ is proportional to the ratio of dynamic shear velocity to the Coriolis parameter, and with strong enough stratification, when $N^2/f^2 \gg 1$, the equation (2) approaches the formula (1).
Elkin et al. [2017] used (1) to estimate the depth of water descent in the Ekman layer on the upper part of the Black Sea continental shelf when a strong northwestern current was present. The result was quite significant: $\sim 20$ m.
This work has the following goals: 1) the experimental study of variability of current velocity, thermohaline parameters and dissolved oxygen concentration in the bottom layer of the Black Sea shelf and upper part of the continental slope; 2) the detection of water transport normal to the shore, and estimation of its scale at different depths; 3) proving the existence of the Ekman dynamics in the BBL.
 |
| Figure 2 |
 |
| Figure 3 |
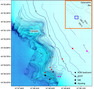
Three long-term (1.5–2 months) installations of autonomous measuring devices were conducted in the shelf-slope area of the Black Sea on the "Gelendzhik" study site of the IO RAS. The devices were set up almost simultaneously in different spots on the site, in the depth range from 80 to 243 m, covering almost the entire area of the Black Sea pycno-halocline (Figure 2 and Figure 3).
 |
| Figure 4 |
Judging by the position of the isopycnal of 16.2 kg/m$^3$, which is considered to be the upper boundary of the hydrogen sulphide contaminated waters, such depth range assuredly covers the zone with variable aerobic/anaerobic conditions. According to the data from multiple studies by the Aqualog profiler, these variations are observed in the water layer from 130 to 220 m (see Figure 4, also [Stunzhas et al., 2018]). The initial conjecture of this study is a possibility of expansion of that zone due to the additional transfer of aerobic water down the slope and anaerobic water up the slope in the Ekman bottom boundary layer.
The following devices were included in the bottom station installations:
During the first installation (15 February–16 April 2018) the measuring stations were situated at the following depths: 80 m – SBE 19 plus; 99 m – SeaGuard RCM DW; 130 m – SeaGuard RCM DW with the optode dissolved oxygen sensor ANDERAA 4330F, also ADCP WHS 1200; 192 m – SeaGuard RCM DW.
For the second installation (31 October–15 December 2018), the station depths were as follows: 135 m – ADCP WHS 1200; 230 m – the Aqualog profiler at the anchored buoy-based station, with the dissolved oxygen sensor SBE 43F connected to the CTD probe; 243 m – SeaGuard RCM DW with the optode dissolved oxygen sensor ANDERAA 4330F.
In the third installation (10 February – 12 April 2019), the stations were at the following depths: 82 m – SBE 19 plus, ADCP WHS 600; 152 m – SeaGuard RCM DW with the optode dissolved oxygen sensor ANDERAA 4330F, also ADCP WHS 600; 212 m – SeaGuard RCM DW; 220 m – the Aqualog profiler at the anchored buoy-based station, with the dissolved oxygen sensor SBE 43F connected to a CTD probe.
Measurement frequency was 10 minutes for all stations except the Aqualog profiler, which conducted vertical profiling once per 1 hour.
Station locations for all three installations are shown in Figure 2. Detailed topographical surveys were performed beforehand for each study period on the shelf and continental slope with the multibeam sonar WASSP WMB-3250. The vertical data resolution of bottom topography was 7.5 cm, horizontal (for a depth of 200 m) – about 1 m. The cross section, normal to the shore, on which the stations were installed, had a relatively smooth topography. There was, however, a canyon north-west of the cross section, whose influence could affect the water dynamics in the studied area.
The purpose of all installations was the long-term measurements of current velocity, CTD-parameters and dissolved oxygen in the BBL. Also, the study took place in the area where conditions changed from aerobic to anaerobic. As mentioned before, the following problems were set: data collection to analyze the possible water transport normal to the shore; estimation of scales of vertical mixing in the BBL and the water column at the same depths; determination of degree of correspondence between water dynamics in the bottom layer and the Ekman boundary layer. To answer the last question, we planned to analyze the connection between the bottom current and the current in the upper layers and to see if there is a presence of a "left turn" in the water flow as it nears the bottom [Taylor and Sarkar, 2008].
Unfortunately, long-term simultaneous measurement of temperature, salinity, density and current velocity profiles in the water column failed. During the first winter-spring installation the Aqualog profiler was not available – it was lost in December 2017, and the reserve unit became available only at the time of the second, autumn installation. During the second study period the pyramid with the bottom ADCP fell on its side, and the current profiles from the 190 m station also became unavailable. The Aqualog profiler, installed at a depth of 230 m, operated irregularly (it appears that there was some mechanical hindrance at the line). Nevertheless, according to its measurements, the current velocity below 190 m was rather small (no more than 12 cm/s; less than 5 cm/s on average), and the Ekman bottom layer most likely would fail to develop in such conditions. Therefore, there was no data that would provide a reliable connection between bottom water transport and currents in the upper layer. During the third installation, the Aqualog profiler, set at a 220 m depth, operated for about two weeks and then stopped because of a failed battery. Still, the collected data were usable to analyze the situation and are presented in this paper.
A preliminary analysis of the data from the first installation confirmed the presence of bottom water transport down the slope, and normal to the shore. An intense alongshore northwestern current causes a descent of water in the bottom layer, and the opposite direction of the alongshore current causes an uprise. As mentioned above, such water transport in the bottom layer and above it quite conforms to the dynamics of a geostrophic flow in the coastal zone of the northeastern part of the Black Sea [Zatsepin et al., 2013]. When an alongshore current penetrates to the bottom, the same manner of water transport should appear in the BBL as well. The Ekman transport, caused by friction on the bottom, should increase normal to shore water movement, induced by the geostrophic adjustment of the density field to the current field. In such a situation the amplitude of the vertical shift of water (and isopycnal surfaces) should be greater in the bottom layer than in the water column, where water moves in a quasi-geostrophic regime. Another symptom of a functioning Ekman bottom layer is the "left turn" of an alongshore current velocity near the bottom. In our case it means that for the coordinate system, which we use for the northeastern part of the Black Sea, when the $x$-axis is directed to the shore and $y$-axis – along the shore and to the left of the $x$-axis, the ratio of the normal to shore velocity component to the alongshore component should be negative and definite (nondegenerate, i.e. above a certain nonzero value) in the BBL. At the same time it should be noted that during weak alongshore currents, according to our data, the water transport in the bottom layer had various directions, lacking any clear correlation with the direction of the alongshore current. It means that the Ekman dynamics is far from being an inherent characteristic of the bottom layer (see "Discussion and Summary" section below).
 |
| Figure 5 |
 |
| Figure 6 |
 |
| Figure 7 |
As an example of the integral Ekman transport down the inclined slope, let us examine a certain event, when the presence of a quasi-homogeneous BBL was registered with a sufficient reliability at the depth about 130 m. This event occurred in the period from 6 to 7 March 2018. Its major properties regarding current velocity in the bottom layer are shown in Figure 5c, Figure 6a, Figure 6b and Figure 7. As seen in the figures, a strong northwestern current existed during the indicated days; its velocity reached 60 cm/s! Such rapid bottom current was never observed during the first installation (Figure 6a). Besides, the 20-m bottom layer was, apparently, well mixed. This follows from Figure 6c, which shows the profiles of velocity magnitude and direction, and Figure 7, where records of current velocity at the bottom (2.5 m) and overlying (15 m) levels are given. As one can clearly see, up until the indicated days, the current velocity on both levels was subject to significant fluctuations in both magnitude and direction. However, during the strong current event the fluctuations were gone. This is an indication that there was no vertical density stratification in the BBL, and a fully developed turbulence existed in this layer. Besides that, there was a significant (up to 10 cm/s) vertical velocity (Figure 5d, upper panel) during an intensified alongshore current velocity (Figure 5d, middle panel). It means that density stratification in the BBL was absent, and water in the bottom layer flowed in accordance with topography, which had a significant inclination, and local relief, the impact of which cannot be accounted for.
A fully developed turbulence in the BBL should result in a profile of vertical velocity following the logarithmic law:
\begin{eqnarray*} U = \frac{U^*}{k} \ln \frac{z}{z_0} + C \end{eqnarray*}Here $U^* = (C_b)^{0.5} \,U_0$, where $C_b$ – bottom friction coefficient, which optimal value for the Black Sea shelf/continental slope is 0.04 [Kushnir, 2007], $U_0$ – current velocity at the upper boundary of the BBL, $k$ – the Karman constant (0.4 for smooth pipes), $z$ – vertical distance from the bottom, $z_0$ – roughness parameter, $C$ – current velocity at $z = z_0$.
Parameterizations of current velocity profiles in the BBL, on a basis of the logarithmic law, was one of the initially set tasks. However, it was found that during the event of 6–7 March, when there was a certainty of a fully developed turbulence in the BBL, the current velocity in the layer of 2.5–20 m from the bottom was generally the same (Figure 5d, Figure 6 and Figure 7). There was also no dominating "left turn" of velocity vectors closer to the bottom. As seen from Figure 6b and Figure 6c, only a small "right turn" was observed during the period of maximal velocity magnitude as the current got closer to the bottom. The "left turn" was registered only at the end of each period of current increase. Generally, this observation confirms the fact that the Ekman circulation should not be formed at once. After the current intensification has begun, it would take a time of $t \approx 1/f$, amounting to several hours, for the Ekman circulation to appear.
The only solid evidence of the integral Ekman transfer in the BBL, directed down the slope, can be seen in Figure 5b, the plot that shows $U_x/U_y$ – the ratio of shoreward current velocity ($U_x$) to the alongshore current velocity ($U_y$), which was measured with the SeaGuard probe in the bottom layer. See also Figure 5d, where three velocity components are plotted, measured by the bottom ADCP 1200 kHz at the same station. It can be seen that during the increase of the northwestern current in 6–7 March, the ratio $U_x/U_y$ was invariably negative: $U_x/U_y \approx -0.2$. Since the typical value of $U_y$ was about 50 cm/c, it means that $U_x \approx -10$ cm/s. About the same negative velocity perpendicular to the shore was registered by the ADCP in the 20-m bottom layer (Figure 5d, lower panel). Figure 5d shows clear a negative correlation between the alongshore (Figure 5d, middle panel) and normal to the shore velocity components, with the latter reaching about $-10$ cm/s during the event. So, how deep down the slope can the BBL water descend, if it moves away from the shore with that velocity?
Let us assume that the descent of the less dense water in the BBL down the inclined slope goes on until it matches the velocity that causes the uprise of fluid and its separation from the bottom due to buoyancy. Taking the velocity of a convective uprise as $U_c = C(BH_b)^{0.5}$, where $B = g \Delta \rho /\rho = N^2 \Delta H$ – water buoyancy in the BBL, $\Delta H$ – depth of the water descent in the BBL due to the Ekman transport relative to the unperturbed state of water in the pycnocline, $C$ – scalar constant, and using the condition $U_x \cos(\alpha) = U_c$, where $\alpha$ – angle of the bottom slope, we can obtain the scale of the descent depth:
\begin{equation} \tag*{(3)} \Delta H \approx \frac{U_x^2 \, \cos^2(\alpha)}{C^2 N^2 H_b} \end{equation}For $U_x = 0.1$ m/s, $H_b = 20$ m, $N = 2 \times 10^{-2}$ s$^{-1}$, $C = 1$ and $\alpha \approx 15$° (Figure 1) we get $\Delta H \approx 2.3$ m. This is a very small value compared with the amplitude of isopycnal fluctuations in the pycno-halocline, which are caused by water column dynamics [Zatsepin et al., 2013]. However, if we take $C = 0.5$, then $\Delta H = 9.2$ m. At the same time, for $H_b = 10$ m, $\Delta H = 18.4$ m. Of course, the equation (3) is a rough estimation that requires verification and elaboration by experimental means including laboratory simulation.
The weak impact of the Ekman transport on density fluctuations and dissolved oxygen concentration in the bottom layer is also confirmed by Figure 5a, which shows that only a little decrease of density and a small amount in the increase of oxygen had occurred after the strong alongshore current event that took place during 6–7 March. At the same time a significant change of those parameters was observed in the period from the second half of 7 March to the second half of 8 March. Water density considerably decreased while dissolved oxygen concentration greatly increased. It appears that an intense cyclonic eddy, passing through the installation point of the SeaGuard and ADCP, was the reason. It created a strong downwelling current, directed south, i.e. practically down the continental slope (Figure 5c). From the second half of 8 March to the second half of 9 March the rear part of the cyclone passed through the bottom station location. The current was directed northwest. A quasi-homogenous BBL was forming, where the current velocity reached 60 cm/s (Figure 7). This event should be followed by the Ekman transport down the slope, however water density continued to increase, and dissolved oxygen concentration kept decreasing (Figure 5a): quasi-geostrophic dynamics caused an upwelling. The sole indication of the existing Ekman transport in the BBL during the described event of the strong alongshore current, just as it was during the previous event of that kind, was the ratio $U_x / U_y < 0$ (Figure 5b).
 |
| Table 1 |
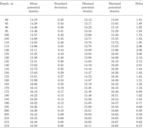
As mentioned above, one of the criteria of effectiveness of water transport, normal to the shore and caused by the Ekman dynamics, is when the amplitude of vertical water oscillations is greater in the BBL than in the water column. Since density is a tracer for the pycnocline water, it is possible to estimate the amplitude of oscillations in different locations in the BBL and water column at corresponding depths. Unfortunately, we were unable to acquire the synchronous data of that kind because of the above described problems with the Aqualog profiler. To compare the amplitude of density oscillations in the BBL and water column at different depths (Table 1) we used the Aqualog data acquired during the cold season of 2015–2016, from 1 November to 1 March (the BBL data used for comparison was from 2018–2019, as described above).
 |
| Table 2 |
The results of comparison are given in Table 2. As can be seen from the table, the isopycnal oscillations in the water column and the bottom layer had very similar amplitude at the same depths. Variability of density values at two levels (130 and 190 m) was higher in the water column, than in the BBL, and only in the case of the top measured level (100 m) was the situation reversed; although all these differences at every depth are lower than the standard deviation.
Comparing the data of dissolved oxygen concentration in the bottom layer at depths of 130 and 150 m yields the following results. Maximal oxygen concentration at 130 m are about 20 times higher than oxygen concentrations at 150 m (228.9 and 12.0 $\mu$M, correspondingly), where the latter, considering average oxygen concentration during the study period, was situated practically at the lower boundary of the oxygen containing layer. During the downwelling period, which was discussed above and caused the descent of oxygen-containing water, the maximal concentration of dissolved oxygen was more that two times higher than during the rest of the entire observation period (228.9 and 102.7 $\mu$M correspondingly); the average concentration of dissolved oxygen increased fourfold (62.2 and 13.8 $\mu$M correspondingly). These 5 days of downwelling increased the average oxygen concentration for the entire observation period by more than 20% (from 13.8 to 16.8 $\mu$M). Therefore even a short-period event of strong downwelling can significantly affect the oxygen regime of the bottom layer.
 |
| Figure 8 |
To provide a descriptive representation of temperature, salinity and density at the three above-mentioned depths in the BBL, all measured values were plotted on the $T-S$ diagram for the first (Figure 8a) and the third (Figure 8b) installations. Different depths are shown as dots of different colors. Figure 8 shows that maximal variability of salinity and density is observed in the area of main pycnocline at a depth of 130 m. Using the mean density profile, averaged for the cold season (Table 1), it is possible to estimate the scale of vertical isopycnal oscillations in the water column. At the depth range of 120–190 m the oscillation amplitude reached 80–90 m and decreased little with depth. These oscillations are caused for the main part by water dynamics, connected with the CIL meandering and mesoscale eddies passing through the bottom stations location [Zatsepin et al., 2013].
 |
| Figure 9 |
A certain intriguing aspect can be seen in the $T-S$ diagram of the third installation (Figure 8b). The diagram shows a clear mismatch of data from the SeaGuard bottom station at 151 m (blue dots) and the Aqualog profiler at the same depth (yellow dots). For the same values of potential density, the Aqualog data are characterized with a water temperature of about 0.1° C less than the SeaGuard data. Assuming there were no artifacts in the measurements, such difference can be explained by the presence of a thermohaline front between the depths of 151 m and 220 m (where the Aqualog profiler was installed), which separates warmer coastal water from the colder water of the open sea. Such fronts are often found during the ecological monitoring, regularly carried out in the same study site, on 9-miles cross sections, by the RV Ashamba (Figure 9). Our future plans include a study of thermohaline fronts in the Black Sea and the determination of their nature and quantitative properties.
An experimental study of current velocity, thermohaline parameters and dissolved oxygen concentration in the bottom layer of the shelf and continental slope of the Black Sea had shown that all these parameters are subject to strong short-period (from several hours to several days) variability. It seems that the main reason for this is the meandering CIL and mesoscale eddies that it caused, which are passing through the measuring stations. Strong changes in the thermohaline parameters and dissolved oxygen concentration in the BBL on the inclined slope in the pycnocline zone (130 m depth) indicate that there is water transport perpendicular to the shore. It was assumed that such movement is partially caused by the Ekman transport [Elkin et al., 2017; Ostrovskii and Zatsepin, 2016; Zatsepin et al., 2007]. However, the data analysis did not support that hypothesis. It seems that the observed transport is almost entirely specified by a geostrophic adjustment of the density field to the current field, and the role of the Ekman transport in the BBL is rather insignificant. This point is also supported by the improved (as compared to [Elkin et al., 2017]) theoretical estimation of water movement in the BBL caused by the integral Ekman transport. Nevertheless, the existence of the integral Ekman transport in the BBL is confirmed by the fact that the ratio of normal to the shore current velocity to alongshore current velocity is mostly negative when intensive currents penetrate down to the bottom. However, a regular "left turn" of current velocity, as the water flow nears the bottom [Taylor and Sarkar, 2008], was not detected in our studies.
This paper mostly ignores the data of the second installation, when the SeaGuard probe was placed at the 243 m depth, and the Aqualog profiler worked (albeit with some interruptions) close to it. Preliminary analysis of the collected data had shown that average current velocity at this depth was very low (about 5 cm/s) and peak values did not exceed 12 cm/s. There were no signs of oxygen intrusions at this level from above. It means that the oxygen inflow mechanism, specified by water dynamics in the bottom boundary layer, can hardly support meiobenthos life at depths of 220–250 m [Stunzhas et al., 2018, 2019].
A thoroughly mixed BBL that was observed only in the periods of most intense bottom current is probably specified by the fact that bottom inclination prevents the formation of the BBL for a highly stratified fluid. Indeed, if isopycnals come up against the inclined bottom, the bottom mixing is followed by isopycnal intrusions penetrating the stratified water, while the stratified water permeates into the BBL [Plaksina et al., 2015]. Because of these exchange processes, the bottom layer constantly restratifies and, in contrast to a non-inclined bottom, there is no sharp density boundary separating it from the overlying water layer. Therefore a development of a well-mixed bottom layer is severely hindered when the inclination angle and density stratification are high enough. It seems that really high values of shear velocity are required, along with a rather prolonged impact, to form the mixed bottom layer in that case. Once it happens, the normal to the shore water transport can be expected to follow the principles of Ekman dynamics. In the case of low shear velocity, however, the Ekman transport in the bottom layer of the stratified fluid on an inclined plane may fail to develop. This problem requires additional experimental and theoretical studies.
Dickey, T. D., J. C. Van Leer (1984) , Observations and simulation of a bottom Ekman Layer on a continental shelf, J. Geophys. Res., 89, no. C2, p. 1983–1988, https://doi.org/10.1029/JC089iC02p01983.
Elkin, D. N., A. G. Zatsepin, A. G. Ostrovskii, et al. (2017) , Sinking of less dense water in the bottom Ekman layer formed by a coastal downwelling current over a sloping bottom, Oceanology, 57, no. 4, p. 531–537, https://doi.org/10.1134/S0001437017040051.
Garrett, C., P. MacCready, P. B. Rhines (1993) , Boundary mixing and arrested Ekman layers: rotating stratified flows near a sloping boundary, Ann. Rev. Fluid Mech., 25, p. 291–323, https://doi.org/10.1146/annurev.fl.25.010193.001451.
Kushnir, V. M. (2007) , Bottom boundary layer in the Black Sea: experimental data, turbulent diffusion, and fluxes, Oceanology, 47, no. 1, p. 33–41, https://doi.org/10.1134/S0001437007010067.
MacCready, P., P. B. Rhines (1993) , Slippery boundary bottom layers on a slope, Phys. Oceanography, 23, no. 1, p. 5–22, https://doi.org/10.1175/1520-0485(1993)023%3C0005:SBBLOA%3E2.0.CO;2.
Ostrovskii, A. G., A. G. Zatsepin (2016) , Intense ventilation of the Black Sea pycnocline due to vertical turbulent exchange in the Rim Current area, Deep-Sea Res. I, 116, p. 1–13, https://doi.org/10.1016/j.dsr.2016.07.011.
Perlin, A., J. N. Moum, J. M. Klymak, et al. (2005) , A modified law-of-the-wall applied to oceanic bottom boundary layers, J. Geophys. Res., 110, p. C10S10, https://doi.org/10.1029/2004JC002310.
Perlin, A., J. N. Moum, J. M. Klymak, et al. (2007) , Organization of stratification, turbulence, and veering in bottom Ekman layers, J. Geophys. Res., 112, p. C05S90, https://doi.org/10.1029/2004JC002641.
Plaksina, M. O., A. M. Pigolkina, D. N. Elkin, et al. (2015) , Gravity current at a sloping bottom in a lineary stratified fluid, Proceedings of the 18th International Conference "Fluxes and Structures in Fluids" A. Ishlinsky institute for problems in mechanics of the RAS, p. 172–175, Kaliningrad State Technical University, Kaliningrad.
Pollard, R. T., P. B. Rhines, R. O. R. Y. Thompson (1973) , The deepening of the wind mixed layer, Geophys. Fluid Dyn., 3, p. 381–404, https://doi.org/10.1080/03091927208236105.
Schaeffer, A., M. Roughan, B. D. Morris (2013) , Cross-shelf dynamics in a Western Boundary Current regime: implications for upwelling, J. Phys. Oceanography, 43, no. 5, p. 1042–1059, https://doi.org/10.1175/JPO-D-14-0091.1.
Stunzhas, P. A., M. B. Gulin, E. A. Ivanova, et al. (2018) , Study of oxygen regime in the near-bottom water layer and reaction of zoobenthos to hypoxia/anoxia at the contact zone of the Black Sea chemocline with continental slope, Some Results of Integrated Coastal Expedition "The Black Sea" Carried out on RV "Ashamba", p. 141–145, Nauchnyi Mir, Moscow (In Russian).
Stunzhas, P. A., M. B. Gulin, A. G. Zatsepin, et al. (2019) , On the possible presence of oxygen in the upper sediment layer of the hydrogen sulfide zone in the Black Sea, Oceanology, 59, no. 1, p. 155–157, https://doi.org/10.1134/S0001437019010211.
Taylor, J. R., S. Sarkar (2008) , Stratification Effects in a Bottom Ekman Layer, J. Phys. Oceanogr., 38, p. 2535–2555, https://doi.org/10.1175/2008JPO3942.1.
Weatherly, G. L. (1972) , A study of the bottom boundary layer of the Florida current, J. of Phys. Oceanogr., 2, no. 1, p. 54–72, https://doi.org/10.1175/1520-0485-2.1.54.
Weatherly, G. L., P. J. Martin (1978) , On the structure and dynamics of the oceanic boundary layer, J. of Physical Oceanography, 8, no. 4, p. 557–570, https://doi.org/10.1175/1520-0485(1978)008%3C0557:OTSADO%3E2.0.CO;2.
Zatsepin, A. G., N. N. Golenko, A. O. Korzh, et al. (2007) , Influence of the dynamics of currents on the hydrophysical structure of the waters and the vertical exchange in the active layer of the Black Sea, Oceanology, 47, no. 3, p. 301–312, https://doi.org/10.1134/S0001437007030022.
Zatsepin, A. G., A. G. Ostrovskii, V. V. Kremenetskiy, et al. (2013) , On the nature of short-period oscillations of the main black sea pycnocline, submesoscale eddies, and response of the marine environment to the catastrophic shower of 2012, Izvestiya. Atmospheric and oceanic physics, 49, no. 6, p. 659–673, https://doi.org/10.1134/S0001433813060145.
Zhurbas, V. M., I. S. Oh, T. Park (2006) , Role of the beta-effect in the decay of the alongshore baroclinic jet associated with transient coastal upwelling and downwelling: numerical experiments, Oceanology, 46, no. 2, p. 170–177, https://doi.org/10.1134/S0001437006020032.
Received 5 November 2019; accepted 18 November 2019; published 10 February 2020.


Citation: Zatsepin A. G., V. V. Kremenetskiy, O. I. Podymov, A. G. Ostrovskii (2020), Study of the effects of Ekman dynamics in the bottom boundary layer on the Black Sea continental slope, Russ. J. Earth Sci., 20, ES1005, doi:10.2205/2020ES000693.
Copyright 2020 by the Geophysical Center RAS.