RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 19, ES5006, doi:10.2205/2019ES000677, 2019
A. G. Simakin1,2
1Institute of the Earth Physics RAS, Moscow, Russia
2Institute of Experimental Mineralogy RAS, Chernogolovka, Russia
Various geodynamic mechanisms can lead to the penetration of siliceous carbonates into the mantle wedge. Their thermal decomposition in the "mantle olivine autoclave" can be a mechanism for the formation of diamond erupted in subduction zone of Kamchatka. Using the theory of poroelasticity, we showed that rapid heating of a mixture of sideritic dolomite and silica on 150–200° C in the closed system conditions can temporarily lead to an increase in the fluid pressure by 2–3 GPa. With the initial parameters $P = 2$ GPa and $T = 830$° C, the carbonic fluid produced during the reaction would get into the PT stability field of the diamond. The growth of diamond at the fluid decomposition in the PT field of metastable graphite can be enhanced by microparticles of native Ni and Mn formed by the thermal decomposition of gaseous metals carbonyls. The corresponding abundant micro-inclusions of Ni and Mn were found in Kamchatka diamonds.

Finding diamonds in active volcanoes in subduction zones is contrary to the generally accepted models of their formation, which require equilibrium PT conditions in the mantle edge [Erlich and Hausel, 2002]. Recently in Russia a new example of such discoveries on the 2012–2013 eruption of Tolbachik volcano (Kamchatka) was published [Silaev et al., 2015]. These diamonds were discovered together with pyroclastics, but not inside it, and their natural origin has not yet been recognized by the global diamond community. A similar situation arises with the Luobusa (Tibet) diamonds found in the podiform chromites 20 years ago [Howell et al., 2015]. These diamonds are also very similar to synthetic high-pressure high-temperature diamonds (HPHT), grown from a carbon solution in an iron-nickel melt. Howell et al. [2015] reported on the results of a comparative study of these diamonds. The authors showed that both synthetic and natural Luobusa diamonds have the same cube and octahedral habitus and numerous metallic inclusions. However, Luobusa diamonds contain predominantly Ni-Mn-Co alloy, while synthetic HTHP diamonds Fe-Ni alloys. The non-aggregative state of nitrogen defects and signs of plastic deformation in natural diamonds indicate a short residence time in the mantle [Howell et al., 2015]. Enriched REE and WC-containing inclusions, present in natural diamonds, as opposed to synthetic ones. In the Avachinsky volcano (Kamchatka) carbonado-like diamonds cemented predominantly with porous silica are described in avachites (basalts with olivine-plagioclase phenocrysts assemblage) [Kaminsky et al., 2016]. These diamonds with respect to the high content of Ni and Mn are similar to those of Tolbachik volcano and Luobusa ophiolites. Kaminsky et al. [2016] proposed a mechanism of diamond formation with the chemical deposition from the vapor phase (CVD) for volcanic diamonds. However, relatively large diamonds from Avacha bear the features of strong deformations, such as dislocation kink-bands and twinning [Kaminsky et al., 2016], as in minerals formed upon impacts. These observations indicate significant deviator stresses at the time of diamond formation [Kaminsky et al., 2016] that contradict to CVD origin at low pressure (several bars or less). Regardless of the actual mechanism for the formation of Kamchatka diamonds, it is clear that the carbonic fluid phase was involved.
Decarbontatisation reactions in the upper mantle are the most probable source of carbonic fluid. Carbonates react with silicates (silica) and generate CO$_2$ and other components (hydrocarbons) in secondary reactions with water and mantle iron-containing minerals buffering fO$_2$. Several basic reactions determine the carbonate-silicate interaction. In general (neglecting contribution of alkalis) the carbonate is represented by dolomite (Ca,Mg,Fe)CO$_3$. It decomposes on aragonite and magnesite at high pressure:
\begin{equation} \tag*{(1)} \mathrm{(Ca,Mg,Fe)CO_3 = CaCO_3 + (Mg,Fe)CO_3} \end{equation}Carbonated iron free lherzolite upon heating releases CO$_2$ by the following reaction [Gudfinnsson and Presnall, 2005]:
\begin{equation} \tag*{(2)} \mathrm{Opx + Dol = Ol + CPx + CO_2} \end{equation}The line of the equilibrium of reaction (2) has a gentle slope in the PT space – the equilibrium pressure is in the range 1.5–2.5 GPa at $1000 < T < 1400$° C. Iron-free dolomite reacts with silica (in the form of stable polymorph coesite) at higher parameters [Luth, 1995]:
\begin{equation} \tag*{(3)} \mathrm{Dol + SiO_2 = Di + CO_2} \end{equation}Pressure of equilibrium is in the range 3–5 GPa at $1000 < T < 1400$° C.
The presence of iron in the dolomite significantly changes the parameters of the decarbontatisation reaction [Martin and Hammouda, 2011].
\begin{equation} \tag*{(4)} \mathrm{Dol - Sid + Cs = Cpx + CO_2} \end{equation}The equilibrium line of the reaction in the PT space is rather steep – at $850 < T < 1200$° C pressure increases from 1.5 to 6.5 GPa, i.e., it is essentially a reaction mediated by the temperature. These parameters are determined for intrinsic fO$_2$ buffered by the presence of FeCO$_3$ (and partially carbon). In more reduced conditions, the equilibrium shifts toward lower temperatures.
Decomposition of the pure siderite was studied experimentally in the pressure range of interest from atmospheric to 20 GPa [Kang et al., 2015]. The equilibrium boundary of reaction
\begin{eqnarray*} \mathrm{FeCO_3 = Fe_3O_4 + C + CO}_2 \end{eqnarray*}is close to the equilibrium in reaction (3) and intersects with graphite – diamond transition line at 5 GPa, 1280° C close to the mantle adiabate and melting point of siderite. At $P=2$ GPa decomposition curve of FeCO$_3$ and the stability boundary of the ferrous dolomite and silica approaches each other at $T=840\mbox{°}$ C. The PT conditions of MnCO3 decomposition are experimentally constrained at atmospheric and rather high (above 15 GPa) pressures [Boulard et al., 2016]. With linear extrapolation from 15 to 2 GPa, the equilibrium temperature is 920° C, which is higher than for the ferrous dolomite [Martin and Hammouda, 2011]. Potentially, MnCO$_3$ or a solid solution of MnCO$_3$–FeCO$_3$ can be a good candidate for the production of diamonds in the mantle wedge. The rapid decomposition of such carbonates in the undrained conditions can in itself increase the pressure to the PT field of diamond stability. However, before the experimental study of the thermal stability of MnCO$_3$–FeCO$_3$ solid solutions at the upper mantle pressures is premature to speculate on this mechanism.
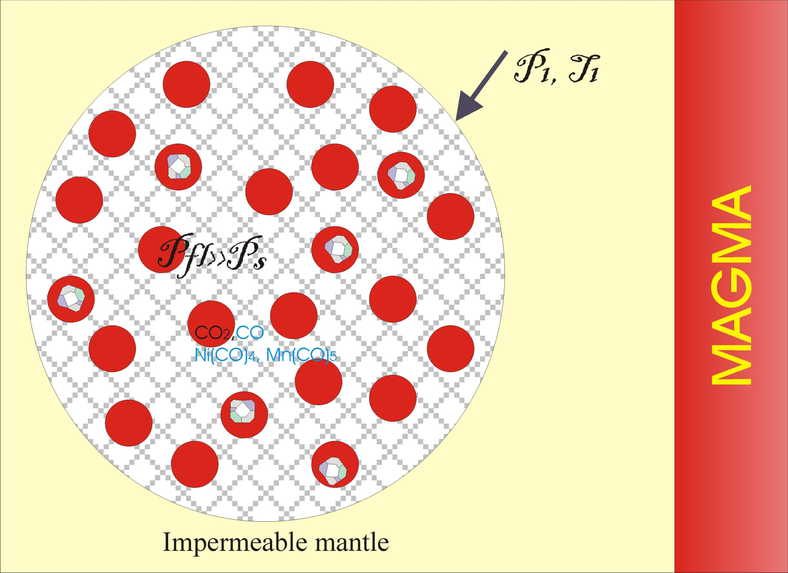
Significant mechanical effects, caused by the reactions with large positive volume effects in the crust such as serpentinization and carbonation are well studied [Fletcher and Merino, 2001; Kelemen and Hirth, 2012]. For metamorphic reactions crystallization pressure is estimated as $P^* = \Delta G_r/ \Delta V_s$ and may exceed 1 GPa [Kelemen and Hirth, 2012]. The level of overpressure is constrained by the shear strength of confining material. The overpressure of 2.4 GPa is recorded in coesite inclusions ($D=15$ mkm) in zircon mono-crystals from the exhumed eclogites partially transformed into quartz with large volume increase [Korsakov et al., 2007]. The pressure in inclusions was fixed near the equilibrium level at low temperature ($P=2.2$ GPa, $T=500$° C, [Swamy et al., 1994]). The transition of coesite to quartz is incomplete, and high overpressure and high local shear stresses were maintained for millions of years due to the high strength of zircon (bulk modulus $K_{\mathrm{zircon}}= 230$ GPa). In the upper mantle at a large confining pressure, shear strength can increase in the fluid free rocks to a level of several hundred MPa, which allows increasing of the overpressure in the reactive volume to a several GPa. Below, we estimate the possible range of pressure increase in a fast (undrained system so that fluid loss and viscous relaxation is negligible) decarbonatisation of a mixture of iron-bearing dolomite and silica when heated by basaltic magma on 150–200° C. Calculations in the poroelastic approximation demonstrate that the PT conditions of diamond stability can be temporarily achieved in the fluid.
 |
| Figure 1 |
In Figure 1, the possible starting point of the carbonate-silica mixture in the PT conditions space is located at $P=2$ GPa and $T= 830$° C near the intersection of the continental geotherm and the equilibrium line of reaction (4). Dashed lines bracket PT conditions of the craton lithosphere, where typical diamonds are formed. For example, the hatched rectangle represents the conditions of the crystallization of eclogite diamonds from Yakutya [Smith et al., 2015] and S. Africa [Nestola et al., 2018]. The CO$_2$ release will increase the fluid pressure limited by the equilibrium parameters of the PT reaction (3) (Figure 1) and can reach the diamond stability field. Among the variants considered above, this situation is possible only for dolomite containing siderite.
The subducting plate beneath the Tolbachik volcano erupting diamonds is located at a depth of 190–200 km (lithostatic pressure of about 6 GPa) [e.g., Seliverstov, 2007]. The pyroxenite source of basaltic magma at a depth of about 100 km or at a lithostatic pressure of about 3 GPa was proposed on the basis of geophysical and general geochemical data [Nikulin et al., 2012]. This assumption was confirmed by our estimate of the pressure in the source of the Tolbachik lava with the formation pressure of chrome-diopside 2.7–3.2 GPa [Simakin et al., 2015].
 |
| Figure 2 |
The presence of carbonates, silicious ooze and coal in the mantle wedge beneath Eastern Kamchatka can be anticipated in connection with the recent accretion of the Kronotsky paleoarc (see references in [Simakin et al., 2014]). Large masses of these sedimentary rocks may be cleaved from the accreted island and dragged beneath Kamchatka to form a sedimentary plume several million years ago [Simakin et al., 2014]. These rocks could be emplaced in the mantle above the level of basaltic magma generation at a depth of 60–70 km (see Figure 2). The conditions of magma generation in Avacha are less clear, distance to the slab is only 120 km there. The temperature in the mantle wedge on Kamchatka was predicted to be much higher than 830° C at $P = 2$ GPa (depth 67 km) [Portnyagin and Manea, 2008]. However, the heat flux near the North Pacific coast of Kamchatka is low in the range 42–47 mW/m$^2$ [Davies, 2013], which corresponds to a low geotherm. This is probably the effect of a thickening of the crust in the accretion zone, and therefore our assumed starting point (2 GPa, 830° C) seems reasonable. Similar PT conditions are expected in the oceanic plate (with the age of 100–120 million years [Davies, 2013]) near Kamchatka. It is predicted that the temperature at a depth of 60 km is about 700° C [McKenzie et al., 2005].
The intersection of the stable silica-carbonate mixture by hot magma may cause decarbonatisation and sudden increase of the fluid pressure to stability parameters of diamond (see Figure 1). When heated, part of the carbonate decomposes and an additional volume $\zeta$ of CO$_2$ is formed. To evaluate the mechanical response to this reaction with increasing of the system volume, the deformation of solid phases and porous rocks will be taken into account within the framework of the theory of poroelasticity [e.g., Cheng, 2016].
Let us assume that the spherical domain of the silica-carbonate aggregate is bounded by a mantle rock with zero porosity. Spherical shell geometry is usual at the consideration of the coupling mechanics and phase transition [e.g., Fletcher and Merino, 2001]. The radius of the inclusion is $R_0$ and the porosity is $\varepsilon_0$, confining pressure equals $P_0$. Poroelastic approximation is valid in a short time limit, since mantle rocks have a relatively low viscosity, so deviatoric stresses will be relaxed with decreasing overpressure. For spherical domain we can write constitutive equations as:
\begin{equation} \tag*{(5)} \sigma_{RR} (r) + \alpha \delta_{ij} P_l(r) = \lambda(\frac{\partial u}{\partial r} + 2 \frac{u}{r}) + 2\mu \frac{\partial u}{\partial r} \end{equation}for the radial component of stress.
\begin{equation} \tag*{(6)} \sigma_{\phi \phi} (r) + \alpha \delta_{ij} P_l(r) = \lambda(\frac{\partial u}{\partial r} + 2 \frac{u}{r}) + 2\mu \frac{u}{r} \end{equation}for the tangential component of stress.
\begin{equation} \tag*{(7)} P_{\mathrm{fl}} = M (\zeta - \alpha (\frac{\partial u}{\partial r} + 2 \frac{u}{r})) \end{equation}for the fluid pressure.
After inserting (7) into (5) and (6)
\begin{equation} \tag*{(8)} \sigma_{RR} (r) + \alpha M \zeta = (\lambda + M \alpha^2 (\frac{\partial u}{\partial r} + 2 \frac{u}{r}) + 2\mu \frac{\partial u}{\partial r} \end{equation} \begin{equation} \tag*{(9)} \sigma_{\phi \phi} (r) + \alpha M \zeta = (\lambda + M \alpha^2 (\frac{\partial u}{\partial r} + 2 \frac{u}{r}) + 2\mu \frac{u}{r} \end{equation}For the shell we can write:
\begin{equation} \tag*{(10)} \sigma_{RR} (r) = \lambda_2 (\frac{\partial u}{\partial r} + 2 \frac{u}{r}) + \mu_2 \frac{\partial u}{\partial r} \end{equation} \begin{equation} \tag*{(11)} \sigma_{\phi \phi} (r) = \lambda_2 (\frac{\partial u}{\partial r} + 2 \frac{u}{r}) + 2 \mu_2 \frac{u}{r} \end{equation}It can be shown (see in the textbooks) that in the case of mechanical equilibrium, the spherically symmetric displacements in the sphere and the shell can be expressed as:
\begin{eqnarray*} u_i = a_i r + b_i / r^2, \qquad i=1,2 \end{eqnarray*}for the internal domain and shell respectively.
At the uniform fluid addition $\zeta(r) = \zeta_0$ constant $b_1 = 0$ and volumetric strain within inclusion is constant
\begin{equation} \tag*{(12)} e_{k k} = \frac{\partial u}{\partial r} + 2 \frac{u}{r} = 3 a_1 \end{equation}Three unknown constants ($a_1$, $a_2$, $b_2$) require the definition of three boundary conditions. These conditions are 1) equality of radial displacements on the boundary:
\begin{equation} \tag*{(13)} r=R_0: \: u_1(R_0)=u_2(R_0) \end{equation}2) equality of the radial components of stresses at the boundary:
\begin{equation} \tag*{(14)} s_{RR,1} (R_0 )= s_{RR,2} (R_0) \end{equation}and 3) vanishing of the radial component of the stress in the shell at infinity:
\begin{equation} \tag*{(15)} s_{RR,2}(\infty) = 0 \end{equation}Solution of the problem (eqn. (8)–(11)) with boundary conditions (eqn. (13)–(15)) for displacements is:
\begin{eqnarray*} a_1 = \frac{\alpha \zeta M}{3(\lambda +M \alpha^2) + 2 (\mu + 2 \mu_2)} \end{eqnarray*} \begin{equation} \tag*{(16)} b_2 = \frac{\alpha \zeta M R_0^3}{3(\lambda + M \alpha^2) + 2 (\mu + 2 \mu_2)}, \quad a_2 =0 \end{equation}Finally, substituting the expressions for the displacements into (7) and (10), (11) we obtain formulas for the excess fluid pressure in the inclusion ($\Delta P_{\mathrm{fl}}$), the maximum tangential stress in the shell on the boundary with the inclusion ($\tau_{\max}$) and the mean stress in the mixture ($\Delta P_s$):
\begin{eqnarray*} \Delta P_{\mathrm{fl}} = \Bigl[\zeta M (( 2 + \frac{K}{K_2})/3 - \nu_2( 4- \frac{K}{K_2})/3\Bigr] \: \Bigl/ \end{eqnarray*} \begin{eqnarray*} \Bigl[ (2 + \frac{K}{K_2})/3 - \nu_2( 4- \frac{K}{K_2})/3 \: + \end{eqnarray*} \begin{equation} \tag*{(17)} M (1 + \nu_2) \alpha^2 / 3K_2 \Bigr]; \end{equation} \begin{eqnarray*} \tau_{\max} = \alpha M \zeta (1 - 2 \nu_2) \Bigl/ \end{eqnarray*} \begin{eqnarray*} \Bigl[ (2 + \frac{K}{K_2})/3 - \nu_2( 4- \frac{K}{K_2})/3 \: + \end{eqnarray*} \begin{equation} \tag*{(18)} M \alpha^2 (1 + \nu_2) / 3K_2 \Bigr]; \end{equation} \begin{eqnarray*} \Delta P_s = 2 \zeta M \alpha K_2 (1 - 2 \nu_2) \Bigl/ \end{eqnarray*} \begin{equation} \tag*{(19)} \Bigl[ (K+ M \alpha^2)(1 + 2 \nu_2) + 2 K_2 (1 - 2 \nu_2) \Bigr], \end{equation}where $K$ and $K_2$ are the bulk moduli of the inclusion and the shell, respectively and $\nu_2$ is Poisson's ratio of the shell. It should be noted that the maximum shear stress in the shell and the overpressure do not depend on the inclusion mixture Poison's ratio $\nu$, which is explained by the hydrostatic inclusion state.
The Biot's module $M$ can be defined experimentally, with some micromechanical model or approximately taken as [Biot and Willis, 1957; Cheng, 2016]
\begin{equation} \tag*{(20)} M= \frac{K}{\varepsilon K/K_f + \alpha - \varepsilon} \end{equation}Biot's constant $\alpha$ for isolated pores is:
\begin{equation} \tag*{(21)} \alpha = \frac{3 \varepsilon ( 1 - \nu)}{2 - 4 \nu + \varepsilon (1 + \nu)} \end{equation}Equations (16)–(21) completely define the solution as a function of the parameters ($\varepsilon, \zeta$) characterizing the progress of the reaction in a closed system.
We use San Carlos olivine parameters for approximating surrounding rock properties. Its bulk modulus at ambient conditions 130 GPa, Poisson's ratio 0.25, at $P=2$ GPa and $T=830$° C $K=125.6$ GPa [Liu et al., 2005] rising to $K=135.3$ at $P=5$ GPa and $T=1100$° C. Physical properties of the reactive mixture at the upper mantle PT conditions can be estimated only approximately since mineral composition and texture have not known and changes in the course of the decarbonatisation reaction. Low-Quartz has the contrasted with other minerals properties: bulk modulus increases from $K=51.7$ GPa at $P=2$ GPa and $T=830$° C to $K=70.8$ at $P=5$ GPa and $T=1100$° C [Swamy et al., 1994]. Poisson's ratio at the ambient conditions is only 0.1. Coesite has the following parameters: $K=99.4$ GPa at $P=2$ GPa and $T=830$° C and $K=121.62$ at $P=5$ GPa and $T=1100$° C [Swamy et al., 1994]. Coesite Poisson's ratio at the ambient conditions is 0.196 [Pabst and Gregorova, 2013]. Polycrystalline dolomite properties are incomplete, temperature dependence of the bulk modulus is unknown. Bulk modulus at ambient conditions $K=93.7$ GPa, $K'P=4.71$ or at pressure $P=2$ GPa [Bakri and Zaoui, 2011] and $T=830$° C $K$ is expected to be about 100 GPa. Dolomite Poisson's ratio at the ambient conditions is 0.268. Diopside at $P=2$ GPa and $T=830\mbox{°}$ C has bulk modulus equal to $K=116.3$ GPa [Li and Neuville, 2010] and at $P=5$ GPa and $T=1100$° C $K=127.8$ GPa. Poisson's ratio at the ambient conditions is 0.242. Thus assuming initial dolomite – low-quartz mixture (75/25 by weight) we get average bulk modulus equal to 87.9. After quartz-coesite transition average $K$ of this mixture will be around 100 GPa. Surrounding rocks are expected to be stiffer with bulk modulus around 130 GPa. Porous rock property is complex function of the properties of its constituents, rock texture and porosity. For the initial guess in our hypothesis we tentatively fix bulk properties at the values close to the presented above.
First we consider the analytical solution of the simplified problem. It is assumed that the fluid formed at the decarbonatisation reaction fills the spherical inclusion in an infinite elastic medium. Solving the equations (10)–(11) with the boundary conditions $S_{RR} = - \Delta P$ at $r = R_0$ and $S_{RR} =0$ $r=\infty$, we can express the relative increase in the inclusion volume due to the excess pressure above the confining pressure $P_0$ (to within linear terms in $P-P_0$)
\begin{equation} \tag*{(22)} \frac{d V}{V} = \frac{( 1 + \nu) (P- P_0)}{2 K_s (1 - \nu)} \end{equation}Suppose that before the start of the reaction there was a fluid with a corresponding porosity $\varepsilon_0$, then the total volume of CO$_2$ at pressure $P$ is equal to $V_{\mathrm{fl}} =(0.733 X_Q /V_0 + \varepsilon_0 \rho_{\mathrm{fl}} (P_0,T_0)) / \rho_{\mathrm{fl}}(P,T)$. The porosity or the total relative initial void volume at the initial pressure $P_0$ is equal to $V^0_{por} = 0.401 X_Q / V_0 + \varepsilon_0$ (here $V_0$ is the volume of the unit mass of the mixture, $X_Q$ is the mass fraction of the reacted silica).
We assume that when the dolomite reacts, the pressure follows an equilibrium path $P=P_{\mathrm{eq}} (T)$. This dependence was taken from [Martin and Hammouda, 2011] and it is linearly extrapolated to pressures lower than that of coesite stability (see Figure 1). Since the volumes of fluid and void are equal
\begin{equation} \tag*{(23)} \frac{V_{\mathrm{fl}} (P, T) - V_{por}^0}{V_{por}^0} = \frac{( 1 + \nu) (P- P_0)}{2 K_s (1 - 2\nu)} \end{equation} |
| Figure 3 |
This equation was solved numerically for pressure at $\nu =0.26$, $K_s=96$ GPa, $P_0=2$ GPa and the solution is displayed in Figure 3. It can be noted that an increase in the initial porosity results in a decrease in the fluid pressure. However, in the entire range of used initial porosity values and the corresponding different mass ratios of the initial fluid and the released CO$_2$, a PT stability field of the diamond is achieved. In this simplified micromechanical model, the average stress in the rock containing the inclusion does not change, and the maximum shear stress is too high 1.5 $P_{\mathrm{fl}}$, higher than shear strength of any rock.
 |
| Figure 4 |
To obtain a more realistic representation of the stressed state of the reacting mixture and host rocks, a complete pore-elastic solution (equations (16)–(21) is used. The theory of poroselasticity has been developed for engineering applications and usually does not operate with such great variations in fluid pressure as in our case (approximately from 2 to 5 GPa). Under the simulated conditions, the compressibility of the fluid (calculated by [Duan and Zhang, 2006]) varies linearly from the pressure in the range $7.9 < K_{\mathrm{fl}} (P_{\mathrm{eq}} (T)) < 21.4$ (GPa). In the calculation of $\zeta$ we use the density of the fluid at the initial pressure $P_0=2$ GPa. The fluid compressibility was iteratively calculated at the midpoint to the pressure corresponding to the current stage of the reaction, expressed in the mass fraction of the reacted silica (see Figure 4). With this choice, the estimated fluid pressure appears to be close to the micromechanical estimate (see Figure 4a).
First, we calculate $P_{\mathrm{fl}}$, the average stress in the reacting matrix, the maximum shear stress in the host rocks before the pressure in the matrix reaches the $\alpha$-quartz-coesite transition level of 2.4 GPa. At this condition $\zeta=0.356$ $X_Q$ and $\varepsilon = \varepsilon_{react} + \varepsilon_0 = 1.126 X_Q + \varepsilon_0$, where $X_Q$ is weight fraction of the reacted silica. At zero initial porosity ($\varepsilon_0 = 0$), the heating to $T < T$ (6.5 GPa) transforms the mixture into a metastable state, since formally at any degree of reaction the pressure will rise above the equilibrium value, i.e. the reaction can not begin. Practically with a low porosity, the degree of decarbonatisation will be small due to a rapid increase in pressure along the equilibrium line. The release of the fluid is accompanied by an increase in the maximum deviatoric stress in the enclosing rocks to 0.6 GPa (at given values of the parameters). With a small initial porosity of not more than 3 vol%, the diamond stability conditions will be reached before the coesite transition. Further heating leads to the transition of $\alpha$-quartz to coesite at an average stress in the matrix of about 2.4 GPa. A decrease in volume during the formation of coesite causes additional porosity, depending on the amount of unreacted $\alpha$-quartz ($X_{0Q} - X_Q$), up to linear terms in $X_{0Q}$ and $X_Q$ total porosity is $\varepsilon = 1.126\: X_Q+ \varepsilon_0 + 0.125(X_{0Q} -X_Q$). In Figure 4a, the calculated fluid pressure is displayed as a function of the total porosity with an initial silica content of $X_{0Q} =0.2$. Coesite transition leads to a decrease in the fluid pressure and a shift of the curves $P_{\mathrm{fl}}(\varepsilon, \varepsilon_0$) to the larger porosities. In Figure 4, the equilibrium parametrization $P(T_{\mathrm{eq}}$) is used, but in fact, under the conditions of the coesite transition, decarbonatisation equilibrium can not be hold. The drop in pressure at a constant $T$ will shift the mixture into a nonequilibrium field. Probably, the coesite transition will lead to an acceleration of the decarbonatisation reaction, which can cause high shear stresses in the host rocks above the shear strength. This can lead to explosive destruction of these rocks and a rapid invasion of the fluid with diamonds into magma. With such an "explosion" deformations of large diamonds with the formation of kink-bands [Kaminsky et al., 2016] are expected. The exsolution of silica from carbonic fluid, subsequently transformed into quartz, which binds Avacha diamonds [Kaminsky et al., 2016], can also be explained by an abrupt pressure drop of several GPa at the failure of host mantle rocks.
It should be emphasized here that the elastic problem does not have its own spatial scale, and therefore the results obtained are equally valid for a large quartz-carbonate domain, for small inclusions and even for several grains. It can be expected that the system has a small size, since only then is rapid heating possible on contact with the magma. At sufficiently large spatial and temporal scales, the viscous relaxation of elastic stresses and the drop in excess fluid pressure become important. An additional argument in favor of the small size of the system in the Kamchatka case is the fact that the findings of diamonds are rather sporadic and in general the geochemical signatures of the interaction of carbonates and basaltic magmas or melting of the carbonatized mantle are weak. Mineralogical evidences of the proposed mechanism of diamonds formation are considered next.
Tolbachin diamonds have anomalously high content, Co (enrichment factor 5–50), Fe (1–2 orders), Ni (1–4 orders) and Mn (3–5 orders of magnitude), as compared to kimberlite diamonds [Silaev et al., 2015]. Absolute concentrations of Ni and Mn in Tolbachik diamonds are $86.3 \pm 68.6$ ppm and $1129.5 \pm 1070.4$ ppm, respectively. In diamonds from Avacha, numerous nanosized (about 50 nm) inclusions of Mn–Si (with traces of Ni and Fe) and Ni–Mn (with traces of Fe and Si) alloys were observed. At the average interparticle distance ca. 2 $\mu$m (estimated for rich Ni rich inclusions with a width of 50 nm in the images from [Kaminsky et al., 2016]) corresponds to a nickel content of about 60 ppm, which is analogous to the content of diamonds in Tolbachik. Diamond-bearing basalts from Tolbachik volcano have high concentrations of Pt (up to 3 ppm) and Co (up to 108 ppm) [Gordeev et al., 2014]. Avacha diamonds are also characterized by the presence of tungsten carbide (WC) with inclusions of native Mn-Fe-Ni-Co alloys [Kaminsky et al., 2016]. Altogether, these mineralogical data may indicate the formation of diamonds from a fluid enriched with different carbonyls or other organometallic compounds. Indeed, the siderophile transition elements (Mn, Fe, Ni, Co, PGE) and W are known to form carbonyls.
We have obtained preliminary experimental data on the solubility of Mn and Pt in a reduced carbonic fluid consisting of CO and CO$_2$ at $P=0.2$ GPa and $T=800-1000$° C and found that these solubilities are at least 250 and 15 ppm respectively [Simakin et al., 2016]. It is estimated that the solubility of nickel in the form of Ni(CO)$_4$ in the reduced carbonic fluid rises from 0.2 to 100 ppm with an increase in pressure from 0.2 to 1 GPa at $T = 900$° C. Our experimental data and thermodynamic calculations indicate the stabilization of carbonyls with increasing pressure and their thermal decomposition. For example, for nickel carbonyl, we calculated that at $P=1$ GPa and $T = 1000$° C, heating on 150° C releases about 60 ppm Ni (based on the weight of the initial fluid solution). Thermodynamic calculations for Ni have not been verified experimentally, solubility can be underestimated since solubility forms differing from Ni(CO)$_4$ are possible. In any case, at the low pressure anticipated for CVD diamond growth [Kaminsky et al., 2016], the solubility of Ni and Mn in the reduced carbon fluid would be small, and the simultaneous crystallization of carbon and metals corresponding to the observed metal concentrations in diamonds would be hardly possible. The low stability of Fe(CO)$_5$ shown with thermodynamic calculations [Simakin et al., 2015], is another argument in favor of the carbonyls involvement in the formation of Kamchatka diamonds. Synthetic HTHP diamonds, grown from the Fe-Ni alloy, have a higher iron content than natural minerals containing more Ni, Mn, Co with stable carbonyls. Enriched REE inclusions [Howell et al., 2015] may indicate reduced carbonic fluid, since REE are also well concentrated and transferred by this fluid [Simakin et al., 2018]. Existing experimental data do not allow unambiguous determination of PT conditions of formation of Kamchatka diamonds based on Ni and Mn concentrations, however, it seems that the pressure was at the level of several GPa.
It should also be emphasized here that carbon precipitates at the disproportionation of CO:
\begin{equation} \tag*{(24)} \mathrm{2CO = C + CO_2} \end{equation}CO in the fluid is a product of the oxidation of wustite and MnO initially produced during MnCO$_3$ and FeCO$_3$ decomposition
\begin{equation} \tag*{(25)} \mathrm{3FeO + CO_2 = Fe_3 O_4 + CO} \end{equation}\begin{equation} \tag*{(26)} \mathrm{2MnO + CO_2 = Mn_2O_3 + CO} \end{equation}
It should be noted that in the reactions (25), (26) and (24), carbon isotopes are fractionated with enrichment of CO and, finally, C (diamond) with light $^{12}$C isotope and carbon dioxide with $^{13}$C. The efficiency of the fractionation of carbon isotopes in a pair of CO$_2$-CO is higher than in a pair of CO$_2$-CH$_4$ [Chacko et al., 2001]. As a result, at a high temperature of 800–900° C, an equilibrium isotopic shift between CO$_2$ and diamond is expected to be about $- (10-17) ‰$. This effect can be enhanced by kinetic factors. Thus, light carbon ($\delta^{13}C = -25.2 \pm 1.3 ‰$) of Kamchatka diamonds [Silaev et al., 2015] can be associated with this mechanism.
Carbonyls can be formed from oxides at the oxygen fugacity above the correspondent metal-oxide equilibrium level.
\begin{equation} \tag*{(27)} \mathrm{MnO + 6\: CO = Mn(CO)_5 +CO_2} \end{equation}There are no thermodynamic data on Mn carbonyl, $\Delta G$ of the reaction (27) can become negative due to high stability of carbonyls and high (several GPa) pressure, since the number of gaseous molecules decreases by four during the reaction.
We observed formation of graphite and Mn transfer in fluid as carbonyls in experiments at $P=0.2$ GPa [Simakin et al., 2016]. Martin and Hammouda [2011] also observed graphite formed due to the disproportionation of CO at the decomposition of FeCO$_3$ (presented as a solid solution with dolomite) in the PT field of diamond stability. Equilibrium concentration of CO at high pressure constrained by CCO buffer reactions is low. However, the high concentration of CO initially produced can be maintained for a period of time before disproportionation. Started after some delay time disproportionation reaction will cause dissociation of carbonyls with native metals formation. The presence of Ni particles with a similar to that of diamond (symmetry group Fm3m with $a= 3.524 {Å}$ and fcc type symmetry group Fd3m with $a= 3.567{Å}$, respectively) can promote the crystallization of precipitated carbon in the form of diamond in this case.
Unusual diamonds found in volcanic rocks of Kamchatka, were formed, certainly, from the fluid. We suggest that the formation of diamond occurs not at low pressure by the CVD mechanism, but rather at PT conditions of their stability. The presence of abundant inclusions of native Ni and Mn can be explained by the thermal decomposition of the corresponding gaseous carbonyls present in reduced carbonic fluid at high pressure. Theoretically, we demonstrated that fluid pressure at the reaction of silica and siderite dolomite caused by magma heating can temporarily increase by 2–2.5 GPa, thus achieving PT stability field of diamond. At the mechanical failure of the pressurized rocks the fluid phase with diamonds is injected into the magma which transfers them to the surface.
Bakri, Z., A. Zaoui (2011) , Structural and mechanical properties of dolomite rock under high pressure conditions: A first-principles study, Phys. Status Solid, B 248, no. 8, p. 1894–1900, https://doi.org/10.1002/pssb.201046465.
Biot, M. A., D. G. Willis (1957) , The elastic coefficients of the theory of consolidation, J. Appl. Mech., 24, p. 594–601.
Boulard, E., Y. Liu, A. L. Koh, M. M. Reagan, J. Stodolna, G. Morard, M. Mezouar, W. L. Mao (2016) , Transformations and Decomposition of MnCO$_3$ at Earth's Lower Mantle Conditions, Frontiers Earth Sci., 4, p. 107, https://doi.org/10.3389/feart.2016.00107.
Chacko, T., D. R. Cole, J. Horita (2001) , Equilibrium Oxygen, Hydrogen and Carbon Isotope Fractionation Factors Applicable to Geologic Systems, Reviews Mineral. Geochem., 43, no. 1, p. 1–81.
Cheng, A. H.-D. (2016) , Poroelasticity, 877 pp., Springer, Switzerland, https://doi.org/10.1007/978-3-319-25202-5 (ISBN 978-3-319-25202-5 (eBook)).
Creon, L., et al. (2016) , Highly CO$_2$-supersaturated melts in the Pannonian lithospheric mantle – A transient carbon reservoir?, Lithos, 286–287, p. 519–533, https://doi.org/10.1016/j.lithos.2016.12.009.
Davies, J. H. (2013) , Global map of solid Earth surface heat flow, Geochemistry, Geophysics, Geosystems, 14, https://doi.org/10.1002/ ggge.20271.
Duan, Z., Z. Zhang (2006) , Equation of state of the H$_2$O, CO$_2$, and H$_2$O–CO$_2$ systems up to 10 GPa and 2573.15 K: Molecular dynamics simulations with ab initio potential surface, Geochim. Cosmochim. Acta, 70, p. 2311–2324.
Erlich, E. I., W. D. Hausel (2002) , Diamond Deposits: Origin, Exploration, and History of Discovery, 374 pp., Society for Mining, Metallurgy, and Exploration, CO, USA (www.smenet.org).
Fletcher, R. C., E. Merino (2001) , Mineral growth in rocks: Kinetic-rheological models of replacement,vein formation, and syntectonic crystallization, Geochim. Cosmochim. Acta, 65, no. 21, p. 3733–3748.
Gordeev, E., G. Karpov, L. Anikin, S. V. Krivovichev, S. K. Filatov, A. V. Antonov, A. A. Ovsyannikov (2014) , Diamonds in lavas of the Tolbachik fissure eruption in Kamchatka, Doklady Earth Sciences (Geochemistry), 454, no. 1, p. 47–49.
Gudfinnsson, G. H., D. C. Presnall (2005) , Continuous gradations among primary carbonatitic, kimberlitic, melilititic, basaltic, picritic, and komatiitic melts in equilibrium with garnet lherzolite at 3–8 Gpa, J. Petrol., 46, no. 8, p. 1645–1659, https://doi.org/10.1093/petrology/egi029.
Howell, D., et al. (2015) , Diamonds in ophiolites: Contamination or a new diamond growth environment?, Earth Planet. Sci. Lett., 430, p. 284–295.
Kaminsky, F. V., R. Wirth, L. P. Anikin, M. Luiz, S. Anja (2016) , Carbonado-like diamond from the Avacha active volcano in Kamchatka, Russia, Lithos, 265, p. 222–236.
Kang, N., M. W. Schmidt, S. Poli, E. Franzolin, J. A. D. Connolly (2015) , Melting of siderite to 20 GPa and thermodynamic properties of FeCO$_3$-melt, Chem. Geol., 400, p. 4–43.
Kelemen, P. B., G. Hirth (2012) , Reaction-driven cracking during retrograde metamorphism: Olivine hydration and carbonation, Earth and Planetary Science Letters, 345–348, p. 81–89.
Korsakov, A. ., D. Hutsebaut, K. Theunissen, P. Vandenabeele, A. S. Stepanov (2007) , Raman mapping of coesite inclusions in garnet from the Kokchetav Massif (Northern Kazakhstan), Spectrochim. Acta, Part A 68, p. 1046–1052.
Levin, V., S. Droznina, M. Gavrilenko, M. J. Carr, S. Senyukov (2014) , Seismically active subcrustal magma source of the Klyuchevskoy volcano in Kamchatka, Russia, Geology, 42, no. 11, p. 983–986, https://doi.org/10.1130/G35972.1.
Li, B., D. R. Neuville (2010) , Elasticity of diopside to 8 GPa and 1073 K and implications for the upper mantle, Phys. Earth Planet. Inter., 183, p. 398–403.
Liu, W., J. Kung, B. Li (2005) , Elasticity of San Carlos olivine to 8 GPa and 1073 K, Geophys. Res. Lett., 32, p. L16301, https://doi.org/10.1029/2005GL023453.
Luth, R. W. (1995) , Experimental determination of the reaction dolomite + 2 coesite = diopside + 2 CO$_2$ to 6 GPa, Contrib. Mineral. Petrol., 122, p. 152–158.
Martin, A. M., T. Hammouda (2011) , Role of iron and reducing conditions on the stability of dolomite + coesite between 4.25 and 6 GPa – a potential mechanism for diamond formation during subduction, Eur. J. Mineral., 23, p. 5–16.
McKenzie, D., J. Jackson, K. Priestley (2005) , Thermal structure of oceanic and continental lithosphere, Earth Planet. Sci. Lett., 233, p. 337–349.
Nestola, F., M. Prencipe, P. Nimis, N. Sgreva, S. H. Perritt, I. L. Chinn, G. Zaffiro (2018) , Toward a robust elastic geobarometry of kyanite inclusions in eclogitic diamonds, J. Geophys. Res., 123, no. 8, p. 6411–6423, https://doi.org/10.1029/2018JB016012.
Nikulin, A., V. Levin, M. Carr, C. Herzberg, M. West (2012) , Evidence for two upper mantle sources driving volcanism in Central Kamchatka, Earth Planet. Sci. Lett., 321–322, p. 14–19.
Pabst, W., E. Gregorova (2013) , Elastic properties of silica polymorphs – a review, Ceramics–Silikáty, 57, no. 3, p. 167–184.
Portnyagin, M., V. C. Manea (2008) , Mantle temperature control on composition of arc magmas along the Central Kamchatka Depression, Geology, 36, p. 519–522.
Seliverstov, N. I. (2007) , Structure of Kamchatka seismofocal zone, Kraunz Bullet. Earth Sci., 9, no. 1, p. 10–26 (in Russian).
Silaev, I., G. A. Karpov, V. I. Rakin, L. P. Anikin, E. A. Vasiliev, V. N. Filippov, V. A. Petrovskiy (2015) , Diamonds in the Products of Tolbachik Fissure Eruption 2012–2013, Kamchatka, Herald of Perm University, 1, no. 26, p. 6–27 (in Russian).
Simakin, A. G. (2014) , Numerical modelling of the late stage of subduction zone transference after an accretion event, Terra Nova, 26, no. 1, p. 22–28.
Simakin, A., T. Salova, V. Devyatova, M. Zelensky (2015) , Reduced carbonic fluid and possible nature of high K magmas of Tolbachik, J. Volcanol. Geoth. Res., 307, p. 210–221.
Simakin, A., T. Salova, R. Gabitov, S. I. Isaenko (2016) , Dry CO$_2$-CO fluid as an important potential Deep Earth solvent, Geofluids, 16, p. 1043–1067.
Simakin, A. G., V. N. Devyatova, T. P. Salova, M. E. Zelensky (2018) , Properties of Reduced Carbon Dioxide Fluid: Evidence from Experimental and Thermodynamic Modeling, Doklady Earth Sciences, 478, no. 1, p. 70–73.
Smith, E. M., M. G. Kopylova, M. L. Frezzotti, V. P. Afanasiev (2015) , Fluid inclusions in Ebelyakh diamonds: Evidence of CO$_2$ liberation in eclogite and the effect of H$_2$O on diamond habit, Lithos, 216–217, p. 106–117.
Swamy, V., S. K. Saxena, B. Sundman, J. Zhang (1994) , A thermodynamic assessment of silica phase diagram, J. Geophys. Res., 99, p. 11,787–11,794.
Tatsumi, Y., H. Shukuno, K. Tani, N. Takahashi, S. Kodaira, T. Kogiso (2008) , Structure and growth of the Izu-Bonin-Mariana arc crust: 2. Role of crust-mantle transformation and the transparent Moho in arc crust evolution, J. Geophys. Res., 113, no. B2, p. B02203, https://doi.org/10.1029/2007JB005121.
Received 14 May 2019; accepted 26 July 2019; published 3 November 2019.


Citation: Simakin A. G. (2019), Poroelastic response to rapid decarbonatisation as a mechanism of the diamonds formation in the mantle wedge of Kamchatka, Russ. J. Earth Sci., 19, ES5006, doi:10.2205/2019ES000677.
Copyright 2019 by the Geophysical Center RAS.