RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 18, ES6006, doi:10.2205/2018ES000646, 2018
Sh. R. Bogoutdinov1,2, N. V. Yagova2, V. A. Pilipenko1,2, S. M. Agayan1
1Geophysical Center of the Russian Academy of Sciences (GC RAS), Moscow, Russia
2Schmidt Institute of Physics of the Earth of the Russian Academy of Sciences (IPE RAS), Moscow, Russia
The results of different algorithms for automatic detection of wave packets in geomagnetic records are compared: the approach based on the Fourier transform in a running time window (F-method), and the approach based on discrete perfect set (DPS) analysis. Using 1-sec data from a mid-latitude INTERMAGNET station we determined with both algorithms such statistical properties of Pc3 geomagnetic pulsations in the frequency range 30–80 mHz as diurnal variations, frequency occurrence, amplitude probability distributions, etc. The diurnal distributions of the occurrence probability determined by both methods have a wide peak around noon hours and a small enhancement during nighttime hours. The advantage of the DPS analysis is the possibility to determine duration of a wave packet. This method shows that average duration of dayside wave packets is statistically longer than that of the nighttime events. Statistical distributions over power/amplitude can be used to infer some conclusions about physical mechanisms of signals. The distribution obtained with the F-method differs for two horizontal components: $H$ component distribution is vulnerable to the magnetospheric resonance effect and reveals parabolic dependence in log-log scale, whereas non-resonant $D$ component has a power-law distribution. The DPS-method provides almost exponential decay of probability with amplitude for both components. The difference between statistical results of two methods is probably caused by different dependences of detection sensitivity to signal amplitude.
In modern geophysics, a rapid growth of the data on processes in the near-Earth space is ongoing. Besides ever-growing expansion of ground based networks of geomagnetic observations, their acquisition systems transfer to a higher sampling rate (e.g., the transfer of INTERMAGNET array from 1 min to 1 sec sampling rate). For efficient use of greatly enlarged database and obtaining qualitatively new results, elaboration of adequate automated methods of system analysis and data processing is required. One of the major problems of the analysis of large volumes of geophysical data is the recognition and classification of desired signals (waves, impulses, noise/turbulence, transients, etc) from long period time series. A good knowledge of morphological properties of desired events puts a basis for revealing anomalous variations caused by catastrophic geophysical phenomena (earthquakes, volcano eruptions, hurricanes) [Rodkin and Pisarenko, 2006]. Moreover, statistical properties of events under study enables one to deduce conclusions about their physical origin using the methods of the inverse statistical theory [Gudzenko, 1962].
Basic physical mechanisms of different types of electromagnetic disturbances in ULF range (from few mHz to tens of Hz) can be reliably established only analyzing the extensive statistics. Development of a necessary database of events under study over a long period runs into the problem of automatic recognition and determination of their key parameters. Automated detection and discrimination of signals with given properties gives a possibility to determine their main morphological features: occurrence rate, diurnal/seasonal variations, dependence on space weather parameters, occurrence-amplitude statistical distributions, etc.
Elaboration of statistical models and relationships is hampered by the lack of effective and flexible tools for automatic selection of characteristic features of a desired phenomenon. Automatic selection of wave events has been commonly made with an algorithm based on the analysis of their power spectral density (PSD) in a running window. Nowadays, this approach is the most widely used in statistical studies of signals from ground, see e.g. [Bortnik et al., 2007], and satellite [Anderson et al., 1990] magnetometers, and for development of new wave power geomagnetic indices [Heilig et al., 2010; Pilipenko et al., 2017; Papadimitriou et al., 2018].
Fourier-based methods are efficient for quasi-monochromatic signals, but these methods become less useful in the analysis of short-lived transients (e.g., Pi2 pulsations), if the time window is long in comparison with the signal duration. Besides, F-method cannot detect precisely start/stop times of continuous pulsations. Therefore, Parkhomov and Stupin [1990] suggested a method of transient signal detection based on the presentation of a signal as a composition of determined and random parts, with subsequent minimization of the functional, describing amplitude temporal evolution. This approach showed a good correspondence with visual detection of Pi2 pulsations in a series of irregular disturbances.
An alternative method of modeling of the logics of an expert-interpreter can be achieved by application of the theory of discrete mathematical analysis (DMA). DMA is a set of algorithms for analysis of digital data, based on fuzzy number comparison, discrete limit, measure of nearness, etc. DMA demonstrated considerable achievements in a number of geophysical applications: retrieval of anomalies in seismic, geoelectric, geomagnetic, and gravity records [Gvishiani et al., 2014; Gvishiani and Lukianova, 2015; Soloviev et al., 2013]. On the basis of DMA, an automated method for anomaly recognition in magnetograms from ground and satellite magnetometers have been implemented [Soloviev et al., 2012]. Algorithmic DMA approach started to be applied to recognize low-amplitude geomagnetic pulsations of different types (Pc3, Pi2, Pc5) [Kleimenova et al., 2013; Zelinsky et al., 2014]. However, the authors of these studies did not try to compare the DMA approach and the standard, much simpler and well-justified, methods based on the Fourier transform. As a result, they did not show so far what new information about signal properties the proposed DMA algorithms could give. In the present paper, we apply a method (named Discrete Perfect Sets – DPS), based on the DMA approach, in which clusters of anomalous disturbance are determined as continuous regions with a relatively high point density, separated from other similar regions by regions with a low point density. We have chosen mid-latitude Pc3 pulsations as a test object for the wave detection with DPS method and its comparison with the method, based on Fourier transform (F-method).
Narrowband Pc3 geomagnetic pulsations in the frequency band 20–80 mHz are observed regularly at middle latitudes almost every day. Moreover, Pc3 pulsations can be detected even at latitudes of the cusp and polar cap [Pilipenko et al., 2008]. Besides common dayside Pc3 pulsations, weak amplitude nightside Pc3 were found [Yagova et al., 2017]. Mid-latitude Pc3–4 waves are commonly recorded in a wide range of local times (LT) from early morning to late evening hours, whereas the maximal amplitudes and occurrence rates are observed in the pre-noon LT sector. These pulsations are considered as a ground image of upstream waves transferred to the ground from the terrestrial foreshock [Engebretson et al., 1991]. The kinetic instability mechanism of Pc3–4 wave generation is very sensitive to interplanetary parameters in the foreshock region: the frequency of upstream waves is determined by the magnitude of the interplanetary magnetic field (IMF) [Gugliel'mi, 1988]; the generation of upstream waves is dependent on the IMF orientation and is most efficient in the region of quasi-parallel bow shock, where IMF cone-angles are small [Bier et al., 2014]; Pc3 wave amplitude has a tendency to increase with growth of the solar wind velocity [Gugliel'mi and Potapov, 1994; Wolfe, 1980; Takahashi et al., 1984]. The wave energy is transported from the foreshock region across the dayside magnetosheath and magnetosphere towards the ionosphere [Clausen et al., 2009]. Upon this propagation, a part of a fast magnetosonic mode energy is resonantly converted into Alfven field line oscillations in the inner magnetosphere [Yumoto, 1988]. Therefore, spectra of ground signals are formed as a combination of the upstream wave spectra and the magnetospheric resonant response [Vellante et al., 1995]. The resonant conversion is most clearly revealed in $H$ component, and much weaker in $D$ component [Pilipenko et al., 1999]. However, many aspects of these notions, in particular possibility of upstream wave penetration through the highly turbulent magnetosheath into the magnetosphere, still remain unresolved and alternative scenarios are discussed [Chugunova et al., 2008].
The structure of the paper is as follows. In Section 2 we give a description of observational data and of both DPS and F techniques of data processing. The results of analysis are given in Section 3, and advantages and drawbacks of each method are discussed in Section 4.
For analysis we have used data from typical mid-latitude station Bay St-Louis (BSL) from INTERMAGNET array with geographic coordinates 30.35${}^{o}$N, 270.36${}^{o}$E, corrected geomagnetic latitude $\Phi$=41.3${}^\circ$, and longitude $\Lambda$= 340.0${}^\circ$, magnetic L-shell, L=1.8, and the magnetic local time MLT=UT-6. We use for the analysis 1-s data (H and $D$ components) recorded during February 01 – March 31, 2015 (days 032–090). Rare interference spikes have been preliminary eliminated with algorithm from [Soloviev et al., 2012].
To validate the obtained statistical distributions, we have compared them with interplanetary parameters from the OMNI database (https://omniweb.gsfc.nasa.gov). During this interval the only moderate geomagnetic storm with Dst =-100 nT took place on March 17, 2015 (DOY=76).
Two different approaches described below have been used and inter-compared for the automatic selection of quasi-periodic signals in the Pc3 band. The methods have been applied separately to $H$ and $D$ component records. In further analysis, we use the frequency band 30–80 mHz. The value of lower end frequency has been chosen to minimize a contribution of Pi2 transients with typical period 1–2 min.
Automatic selection of Pc3 events has been made with an algorithm based on the analysis of PSD, calculated with Blackmann-Tukey technique [Kay, 1988], in a running window with duration 12.8 min with 3-min time step. This method was applied earlier for automatic selection of Pc2–3 pulsations recorded in space [Yagova et al., 2015] and on the ground [Yagova et al., 2017].
 |
| Figure 1 |
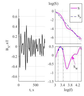
A log-log spectrum $S(\overline{f}$) is linearly detrended ("whitened") as $S_W\left(\overline{f}\right)=S\left(\overline{f}\right)-S_P(\overline{f})$ for each interval, where $S_P(\overline{f})$ is the best linear fit of $S(\overline{f})$, $S=\log(S_f)$, $S_f$ is the power spectral density at frequency $f$, and $\overline{f}=\log(f)$ (see illustration in Figure 1). In a $\Delta \overline{f}$ vicinity of $\overline{f}=\overline{f_c}$, where $S_W$ reaches a maximum, $S_W(\overline{f})$ is approximated by a square polynomial $S_W\left(\overline{f}\right)=-a_2\left(\overline{f}-{\overline{f}}_c\right)+S_0$. A periodic signal is considered to be detected when both $S_0$ and $a_2$ exceed some threshold values $S_b$ and $a_b$. In the present study, we use the frequency range 30–80 mHz, and threshold values $S_b=-0.5$, and $a_b=0.5$. The selected parameter set corresponds to threshold amplitudes $\sim$0.2 nT. This method is based on parameters of intervals of fixed length. Thus it cannot determine a number of wave packets and their duration in a given time interval.
The F-method enables one to determine hourly/daily values of the following wave parameters:
This method helps to decide whether a set of some measure of disturbance above a certain threshold belongs to the same signal or not. As a first step, the Butterworth bandpass filter of 6-th order in the frequency range 30–80 mHz has been applied. This filter has a smooth amplitude-frequency response and has a minimal phase distortion [Parks and Burrus, 1987]. The 6-th order filter was chosen as it gives the optimal combination of steep decrease at the ends and absence of disturbances specific for higher order filters.
 |
| Figure 2 |
We introduce such DPS parameters like energy and length of a signal, and explain what new information about a signal under study they can provide. The algorithm is illustrated in Figure 2. The DPS algorithm is based on the notion of density of multi-dimentional data array $P_{A} (x)$ in each point $x$. If $X$ is a finite manifold with the standard metric $d$, and $A$ is a subset of $X$, then the density $P_{A} (x)$ is introduced by the formula
\begin{equation} \tag*{(1)} P_{A} (x)=\sum _{y\in B_{A} (x,r)} \left(1-\frac{d(x,y)}{r} \right), \end{equation}where $B_{A} (x,r)$ is a closed sphere in $A$ with radius $r$ and origin in $x$. The localization radius $r_{q} (X)$ is determined as power-mean under negative parameter $q<0$ of all the distances $D(X)$:
\begin{equation} \tag*{(2)} r_{q} (X)=\left(\frac{\sum d^{q} }{|D(X)|} \right)^{{\kern 1pt} 1\; {\kern 1pt} /{\kern 1pt} q\; {\kern 1pt} } \end{equation}Here $|D(X)|$ denotes the number of elements in the manifold $D(X)$.
The DPS algorithm construct the manifold $X(\alpha )$ with its density higher than the level $\alpha $ in all points. If the density $P_{A} (x)$ is a measure of limitness of the point $x$ for the manifold $A$ and all points with $P_{A} (x)> \alpha $ are limiting points, then the manifold $X(\alpha )$ coincides with the manifold of its limiting points. In this sense $X(\alpha )$ is an analogue of topologically perfect manifold.
The selection of anomalies (signals) in time series $f(x)$ in the time interval $X=[a,b]$ and subsequent clusterization are performed in the following way (Figure 2a). A disturbance is measured as absolute values of the band-filtered (with Butterworth filter) time series $\bar{f}(x)$ (Figure 2b). Then, for sub-manifold $A\subseteq X$ the density $P_{A} (x)$ is determined as a sum of the function $\overline{f}(x)$ in the interval $\Delta$ surrounding the point $x$ (Figure 2c). For the constructed density, we apply the DPS algorithm. As a result, we obtain a set of intervals with detected signals (Figure 2d) $X=\{ [a_{1} ,b_{1} ],\ldots ,[a_{n} ,b_{n} ]\} $. The distance between intervals is determined as
\begin{eqnarray*} \rho ([a_{1} ,b_{1} ],[a_{2} ,b_{2} ])=\frac{|[a_{1} ,b_{1} ]|+|[a_{2} ,b_{2} ]|}{|\min (a_{1} ,a_{2} ),\max (b_{1} ,b_{2} )|} \end{eqnarray*}Using the distance $\rho$, the density of the interval $[a,b]$ can be constructed for $A\subseteq X$ as follows
\begin{eqnarray*} P_{A} ([a,b])=\mathop{\max }\limits_{} ([a,b],[a_{1} ,b_{1} ]) \end{eqnarray*}Applying the DPS algorithm for the set of intervals $X$ for some $A$ and $\beta $, we obtain the manifold of united intervals. By red color in Figure 2e the results of fist step of the DPS algorithm are marked. The results of two subsequent steps and final reduction of the results to the given time series are shown in Figure 2f. The DPS method enables one to determine:
The DPS algorithm detects an anomaly (signal) above a local background. Thus, depending on the level of background fluctuations, the threshold for selected signals may vary.
Both methods are compared with visually selected Pc3s for the days 32–45. For the F-method the detection is based on two parameters: PSD $S_{0}$ at the central frequency, and the $a_{2}$ coefficient of the square approximation in log-log scale. To verify the method, the distributions of both parameters for visually selected Pc3 intervals and for the general sample are compared, and the complex of the form Cr${}_{F}=a_{2}-\alpha \log(S_{0})$ is constructed.
For the DPS method, the verification was carried out by calculating probabilities of four cases:
Here $t_{ik}$ $(i,k=0,1)$ is a total duration of Pc3s selected by both DMS and visual inspection ($t_{11}$), one of the methods ($t_{01}$, $t_{10}$), and none of the methods ($t_{00}$), and $t$ is the total duration of all intervals analyzed. The coincidence probability is then defined as $Pc=(t_{11} + t_{00})/t$, and P${}_{10}$ and P${}_{01}$ correspond to false detection and lost signal, respectively.
Below, we give a comparison of the statistical relationships obtained using with the two methods of Pc3 detection. We have analyzed day-to-day variations of Pc3 occurrence rate and averaged statistical distributions over the whole observational period. We also compare Pc3 occurrence rates with the solar wind speed $V$ and geomagnetic activity to validate the results of the detection techniques developed in the present study with the regularities known for Pc3s from earlier studies.
 |
| Figure 3 |
Day-to-day variations of daily occurrence rate $P$ during the entire period under study are given in Figure 3. Two upper panels present the results, obtained by F and DPS methods for two horizontal components ($H$ and $D$). Daily mean values of the solar wind velocity $V$ and Dst index are given in the bottom panels. Time periods with large $P$ coincide with periods of high $V$. The Pc3 probability is higher for $H$ component than that for $D$ component. During high $V$, the daily Pc3 occurrence rate reaches $\sim$40%. The majority of maxima of $N$ coincide for both components, however, several maxima are seen only in the $H$ component under moderate $V$.
Both methods give similar, but not identical day-to-day variations. A difference in absolute values of $P$, obtained by two methods is natural, because of different threshold amplitudes. Besides, some of peaks, seen predominantly in $H$ component, can be shifted at 1 day. However, the most important features of day-to-day variations agree. During the magnetic storm on March, 17 (Day 76) a maximum of $P$ is observed. Its value is close to those seen during the recovery phase (Days 80, 84) and for the non-storm days with high $V$ (days 33, 60, 66). This result agrees with a well known fact, that moderate geomagnetic activity and high solar wind speed are favorable for Pc3 wave generation [Gugliel'mi and Troitskaya, 1973]. High speed streams are often followed by auroral activations, therefore the Pc3 occurrence coincides with both V (Figure 3c) and AE index (Figure 3d). However, the discrimination between the effect of solar wind velocity and auroral activation is beyond the framework of this study.
 |
| Figure 4 |
F-method. Diurnal variations of Pc3 occurrence rate $P$ and PSD are given in Figure 4. $P$ has a broad maximum, reaching 0.55 for H-component at pre-noon hours at 10–11 MLT. For $D$ component, it is nearly two times lower, though the forms of both variations are similar. The obtained diurnal distribution reproduces a well known diurnal variation for mid-latitude Pc3 pulsations [Gugliel'mi and Troitskaya, 1973].
The bottom panel presents normalized diurnal variation of PSD at frequency of spectral maximum $S_{0}$. The parameter $S_{0}$ is approximately proportional to an average amplitude of Pc3 wave packet in time window. $H$ component maximal power exceeds almost twice $D$ component maximal power. $H$ component power exceeds 1/2 of its maximum value from 6 to 15 MLT, while for $D$ component Pc3 energy exceeds 1/2 of its maximum value only at pre-noon hours. A weak enhancement of H-component power is seen also near local midnight.
 |
| Figure 5 |
DPS method. The diurnal variation of DPS-detected Pc3 amplitude averaged over the observational period is given in Figure 5.
The DPS method gives qualitatively the same results as the F-method with the maximum at pre-noon hours and higher amplitudes for $H$ component. The $H$ component amplitudes about 0.5 nT agree with typical values of amplitudes of mid-latitude Pc3s. However, both H/D ratio and day/night amplitude ratios are higher in comparison with those obtained with the F-method. This is the result of contribution of broadband background into PSD determined by the F-method, while DPS analysis selects the signal less contaminated by background fluctuations.
 |
| Figure 6 |
The event duration can be determined with the DPS method. The averaged diurnal variation of Pc3 wave packet duration is given in Figure 6. It is worth noting, that the DPS does not select an isolated wave packet, but an event when the signal amplitude in the given frequency band is in some approximation higher in comparison with the background.
During daytime hours the average wave packet length is about 600–800 s (i.e. it varies from 10 to 30 periods for 30 s pulsations). Duration of most events at nightside do not exceed 200 s.
 |
| Figure 7 |
F-method. The statistics of central frequencies $f_c$ of detected wave packets is characterized by the empirical probability density function $P^{\star}$ (Figure 7, left-hand panel). The $f_c$ of $D$ component has a maximum at in 35–40 mHz frequency band, while $H$ component distribution is shifted to higher frequencies and has a broad maximum around 50 mHz. This frequency highly probably corresponds to the frequency of the field line resonance at this latitude.
We have also calculated the difference $\Delta f$ between the detected values of $f_c$ and the frequencies of upstream waves predicted from the statistical relation between Pc3 frequency and the IMF magnitude $f_B=6B$, where $f_{B}$ is the wave frequency in mHz, and $B$ is the IMF magnitude in nT [Gugliel'mi, 1988]. The empirical probability density functions for both horizontal components are given at right-hand pane of Figure 6. It is seen that $D$ component has an off-set centered at $\Delta f=5 $nT, while $H$ component is characterized by a larger shift to a high-frequency side of the distribution.
Thus, $D$ component corresponds better to upstream wave frequency. This component ought to be used to improve the "Borok B-index" proposed to predict IMF $B$ magnitude from ground Pc3–4 data [Russell and Fleming, 1976]. A non-zero value of the most probable $\Delta f$ is probably related with a shift to higher frequencies of a maximum determined from a whitened spectrum [Ponomarenko et al., 2002].
We use the integral (cumulative) probability function $F(S)$ determined as probability of power/amplitude to exceed $S$. $F(S)$ is derived from the observation data at BSL for both horizontal components.
 |
| Figure 8 |
F-method. For $D$ component, $F(S)$ is close to power dependence $F(S)\propto S^{-\alpha }$ with $\alpha$=1.2. It is shown in Figure 8, where the dependence $F(S)$ is given in log-log scale together with the linear fit. The agreement is perfect for all the values of $S$ with the exception of very low energies, near the threshold PSD value.
On the contrary, the $H$ component power distribution is a nonlinear at all the PSD values. It can be described with the square approximation in log-log scale (dashed line), i.e. the decrease of $F(S)$ is quicker than the power law and slower than the exponential function.
We suppose, that the difference between the two components in the power dependence of the integral probability function can be the result of influence of the local magnetospheric resonance effects on $H$ component.
 |
| Figure 9 |
DPS method. The statistical distribution of cumulative probability function $F(A)$ is shown in Figure 9 for $H$ component (left panel) and $D$ component (right panel).
The distribution shows an evident change of slope at very large amplitudes, $\sim$13 nT. However, nearly all range of possible amplitudes is well described by a straight line in a log-linear scale. Thus, the distributions for both components can be approximated by the exponential function $F\left(A\right)\propto {\mathrm{exp} \left(-{A}/{A_0}\right). }$
The difference with the results obtained by the F-method is probably related to the bias inherent to the DPS method – a higher sensitivity to weak signals at a low level background.
 |
| Figure 10 |
Both methods used here are aimed at the substituting of the visual inspection rather in the time, than in the frequency domain. To test their validity for this purpose, the Pc pulsations were visually selected from the BSL high-pass filtered ($f_c$=6 mHz) magnetograms for days from 32 to 45 (see the Dataset of visually selected Pc3s in the ESDB by Bogoutdinov et al., [2018]) and classified into three classes from doubtful (0) to high quality (2) (1). The two methods give different information about the pulsations. While the F-method deals with the fixed length interval, it cannot give a one-to-one correspondence to any selection procedure, which is directly based on the time domain. However, the distributions for $a_2$ and $S_0$ parameters differ essentially for the general sample and for the visually selected Pc3s. This allowed to construct a complex Cr${}_{F}=a_{2}-\alpha \log(S_{0})$, which at $\alpha$=3 and Cr${}_{F}$ $>$-5 gives a more than 75% correspondence to visually selected pulsations (Figure 10).
The selection is done for all the Pc3s with quality flag not less than 1. Thus, the F-method gives a probability criterium which can be fitted either to select all the events and an essential number of empty intervals, or it will miss doubtful events. Nonetheless, all the selected events will contain Pc pulsations.
The test for the DPS method is based on the probabilities for four possible cases: Success rate $P_{S}=P_{11} + P_{00}$, where $P_{11}$ and $P_{00}$ are the probabilities of true detection of an event and of an empty interval, $P_{10}$ and $P_{01}$ are the probabilities of false detection of an event and missed event, respectively. The values of corresponding probabilities for the days given in the Table in Appendix are equal to $P_{S}$=0.73, $P_{10}$=0.15, and $P_{01}$=0.12, i.e. both methods give close averaged efficiency in comparison with visual inspection.
We have compared the two algorithms for automatic detection of Pc3 (30–80 mHz) wave packets in geomagnetic records: the approach based on the Fourier transform (F-method), and the approach based on discrete perfect set (DPS) analysis, using as a test 1-sec data from a mid-latitude INTERMAGNET station. The basic statistical features, i.e. diurnal and day-to-day variations, determined with both algorithms, have turned out to be similar. Although several peculiarities are seen only in $H$ component. While the majority maxima of day-to-day variation of $D$ component Pc3 occurrence correspond to intervals of high solar wind speed $V$, day-to-day variation of $H$ component Pc3 occurrence demonstrates several maxima not seen neither in $D$ component, nor in $V$ (Figure 3, upper panel). However, the interplanetary information we have used is not complete. The significant factor which controls the excitation efficiency of Pc3 upstream waves is the cone angle (angle between IMF and normal to the bow shock) [Bier et al., 2014]. This angle is fast varying and has not been considered.
The most important factor inside the magnetosphere which influences the Pc3 generation is the auroral activity (see [Parkhomov et al., 1988] and references therein). An auroral activation is not only a source of nighttime Pc3s, but it can influence dayside Pc3s, as well. [Parkhomov et al., 1988] reported that a substrorm at nightside can trigger morning Pc3s. The problem of classification for substorm related pulsations is also ambiguous, because along with pure Pc3s, higher Pi2 harmonics, Pi1c pulsations and contribute the spectral power at Pc3 frequencies. The morphological discrimination between these subclasses is difficult (if ever possible), and we understand that any of these pulsations are classified as Pc3s by each of the methods applied.
The different statistical features of two horizontal components are probably related to different contributions of external source features and field-line resonance in the magnetosphere into the pulsation spectra for $H$ and $D$ components. Thanks to field line resonance, $H$ component acquires a higher spectral power and more narrow-band spectrum as compared with $D$ component. On the contrary, $D$ component is more source dependent [Pilipenko et al., 1999]. The distribution of $D$ component Pc3s over central frequency $f_{C}$ demonstrates a relatively good agreement with the $f_{B}$=6$B$ relation (Figure 6). Hence, $\Delta f=f_C-f_B$ distribution of $D$ component Pc3s is centered at low positive $\Delta f$.
A form of the occurrence-amplitude distribution provides information about physics of a process under examination [Rodkin and Pisarenko, 2006]. For example, when variations of the parameter is due to independent random action of several factors produce the normal (Gaussian) probability density distribution is obtained. The energy of components in an isolated system is distributed as the exponential Boltzmann or double-exponential (Laplace) distribution. The self-similar power law distribution is often attributed to the result of self-organized criticality in a system under study [Uritsky et al., 2004]. An accidental choice from several parameters produces a log-normal distribution. In many cases in natural world heavy-tailed probability distributions are ubiquitous. Knowledge of the probability distribution of fluctuations can provide insight into underlying dynamical processes.
The F-method shows an essential qualitative difference between $F(S)$ dependences for $H$ and $D$ components. While $F(S)$ dependence of $D$ component is with a good accuracy approximated by a power law, the dependence for $H$ component in log-log presentation can be approximated with a square polynomial. This means, that integral probability function $F(S)$ decreases with S slower than a power function $S^{-\alpha }$ at low $S$, and it falls quicker than it at high $S$. Another possibility is to model this distribution as two power-laws (straight lines in log-log scale) with change of slope at $S \sim$1 nT${}^{2}$/Hz, corresponding to spectral amplitude $A_{f} \sim$0.03 nT/mHz${}^{1/2}$.${}^{ }$ However, this modeling function has a weaker correlation with measured distribution (according to Kolmogorov-Smirnov test) than the quadratic power-law dependence.
According to the F-method, $F(S)$ distribution has a longer tail that the exponential distribution determined by the DPS-method. Probably, this fact may be a result of an integral effect of lower frequency resonances met during upstream waves propagation at upper $L$-shells. A more detailed consideration of possible physical mechanisms of the difference in power distribution for $H$ and $D$ components will done elsewhere.
The presented algorithms needs a further advancement. Probably, a combination of two methods would give a more effective tool of automatic detection of Pc pulsations and quantification of wave parameters, than each of the methods, taken alone. A principle advantage of the DPS method is the variable time window. The latter is determined by a wave amplitude and spectrum, and it allows to include into analysis duration of a wave packet. This information is missed in techniques, based on the spectral characteristics of calculated for a fixed time window. However, power analysis in F-method is more accurate, as it is based on absolute values of power spectral density. Thus, a combined method can use DPS for signal detection and time parameters, and F-method for energetic parameters.
Along with a well known applications of Pc3–5 pulsations for magnetospheric sounding, some types of pulsations can be a source of extreme disturbances of magnetic field at auroral and sub-auroral latitudes. Powerful Pc5/Pi3 (1–5 mHz) pulsations of specific spectral content can generate geomagnetically induced currents (GICs) potentially dangerous for electric power lines [Yagova et al., 2018]. For the GIC problem, the technique of analysis, which is developed and verified in the present study for a relatively simple case of mid-latitude Pc3 pulsations, should be modified for a more complicated case of high-latitude Pc5/Pi3 with non-sinusoidal form.
The algorithms for automatic detection of Pc3 (30–80 mHz) wave packets, based on the Fourier transform (F-method), and based on discrete perfect set (DPS) analysis, using as a test 1-sec data from a mid-latitude INTERMAGNET station provided similar basic statistical features, such as diurnal and day-to-day variations.
However, both methods have certain advantages and drawbacks. The DPS method as compared with the F-method has a bias: it is more sensitive to weak signals. The DPS method enables one to determine not only the parameters of an interval with fixed length (occurrence probability, power), but the average signal duration.
The statistical distribution of power of Pc3 wave packets, characterized by the probability function $F(S)$ differ for two methods. F-method has revealed a qualitative difference between two horizontal components, probably related to field line resonances. On the contrary, DPS methods predicts exponential decay of integral probability function for both components. A combination of the two methods may provide a powerful tool for automatic detection and quantitative analysis of pulsation parameters for different applications, including GIC generation in electric power lines.
Anderson, B. J., M. J. Engebretson, S. P. Rounds, et al. (1990), A statistical study of Pc 3–5 pulsations observed by the AMPTE/CCE Magnetic Fields Experiment, 1. Occurrence distributions, JGR: Space Physics, 95, no. A7, p. 10249–10723, https://doi.org/10.1029/JA095iA07p10495.
Bier, E. A., N. Owusu, M. J. Engebretson, J. L. Posch, M. R. Lessard, V. A. Pilipenko (2014), Investigating the IMF cone angle control of Pc3–4 pulsations observed on the ground, JGR: Space Physics, 119, no. 3, p. 1797–1813, https://doi.org/10.1002/2013JA019637.
Bogoutdinov, Sh. R., N. V. Yagova, V. A. Pilipenko, S. M. Agayan (2018), Dataset of visually selected Pc3s, ESDB, GC RAS, Moscow, https://doi.org/10.2205/RJES-data-646.
Bortnik, J., J. W. Cutler, C. Dunson, T. Bleier (2007), An automatic wave detection algorithm applied to Pc1 pulsations, JGR: Space Physics, 112, no. A4, p. A04204 1–12, https://doi.org/10.1029/2006JA011900.
Chugunova, O., V. Pilipenko, G. Zastenker, et al. (2008), Magnetosheath turbulence and magnetospheric Pc3 pulsations, Proc. of the 7-th International Conference "Problems of Geocosmos", edited by V. N. Troyan, M. Hayakawa, and V. S. Semenov, St. Petersburg.
Clausen, L.B.N., T.K. Yeoman, C. Fear R.C., et al. (2009), First simultaneous measurements of waves generated at the bow shock in the solar wind, the magnetosphere and on the ground, Annales Geophysicae, 27, no. 1, p. 357–371, https://doi.org/10.5194/angeo-27-357-2009.
Engebretson, M.J., N. Lin, W. Baumjohann R.C., et al. (1991), A comparison of ULF fluctuations in the solar wind, magnetosheath, and dayside magnetosphere: 1. Magnetosheath morphology, JGR: Space Physics, 96, no. A3, p. 3441–3454, https://doi.org/10.1029/90JA02101.
Gudzenko, L.I. (1962), Statistical method to determine the characteristics of non-controlled auto-oscillatory system, Radiophysics and Quantum Electronics, 5, no. 3, p. 572–586.
Gugliel'mi, A.V. (1988), The coefficient of relationship between the Pc3 pulsation frequency and IMF magnitude, Geomagnetism and Aeronomy, no. 28, p. 465–468.
Gugliel'mi, A.V., A.S. Potapov (1994), Note on the dependence of Pc3–4 activity on the solar wind velocity, Annales Geophysicae, 12, no. 12, p. 1192–1196, https://doi.org/10.1007/s00585-994-1192-z.
Gugliel'mi, A.V., V.A. Troitskaya (1973), Geomagnetic pulsations and diagnostics of the magnetosphere, 206 pp., Nauka, Moscow.
Gvishiani, A., R. Lukianova, A. Soloviev, et al. (2014), Survey of geomagnetic observations made in Northern Russia and new methods for analyzing them, Surveys Geophysics, 35, no. 5, p. 1123–1154, https://doi.org/10.1007/s10712-014-9297-8.
Gvishiani, A.D., R.Y. Lukianova (2015), Geoinformatics and observations of the Earth's magnetic field: the Russian segment, Izvestiya-Physics of the Solid Earth, 51, no. 2, p. 157–175, https://doi.org/10.1134/S1069351315020044.
Heilig, B., S. Lotz, J. Vero, P. Sutcliffe, J. Reda, K. Pajunpaa, T. Raita (2010), Empirically modeled Pc3 activity based on solar wind parameters, Annales Geophysicae, 28, no. 9, p. 1703–1722, https://doi.org/10.5194/angeo-28-1703-2010.
Kay, S.M. (1988), Modern spectral estimation: Theory and application, 543 pp., Prentice-Hall, New Jersey, USA.
Kleimenova, N.G., O.V. Kozyreva, L.M. Malysheva, N.R. Zelinskii, A.A. Solov'ev, S.R. Bogoutdinov (2013), Pc3 geomagnetic pulsations at near-equatorial latitudes at the initial phase of the magnetic storm of April 5, 2010, Geomagnetism and Aeronomy, 53, no. 3, p. 313–320, https://doi.org/10.5194/angeo-28-1703-2010.
Papadimitriou, C., G. Balasis, I.A. Daglis, et al. (2018), An initial ULF wave index derived from two years of Swarm observations, Annales Geophysicae, 36, no. 2, p. 287–299, https://doi.org/10.5194/angeo-36-287-2018.
Parkhomov, V.A., T. N. Polyushkina, V.V. Stupin (1988), The increase of geomagnetic pulsation activity in the Pc3 range during magnetospheric substorms, Research in Geomagn., Aer. And Solar Physics, 81, p. 188–199.
Parkhomov, V.A., V.V. Stupin (1990), Identification of geomagnetic pulsations simulation methods in the problems of magnetospheric diagnostics, Geomagnetism and Aeronomy, 30, no. 1, p. 44–49.
Parks, T.W., C.S. Burrus (1987), Digital filter design, 342 pp., Wiley, New York, USA.
Pilipenko, V., K. Yumoto, E. Fedorov, N. Yagova (1999), Hydromagnetic spectroscopy of the magnetosphere with Pc3 geomagnetic pulsations at 210 meridian, Geomagnetism and Aeronomy, 17, no. 1, p. 53–65, https://doi.org/10.1007/s00585-999-0053-1.
Pilipenko, V.A., O.M. Chugunova, M.J. Engebretson (2008), Pc3–4 ULF waves at polar latitudes, Journal of Atmospheric and Solar-Terrestrial Physics, 70, no. 18, p. 2262–2274, https://doi.org/10.1016/j.jastp.2008.09.006.
Pilipenko, V.A., O.V. Kozyreva, M.J. Engebretson, A.A. Soloviev (2017), ULF wave power index for the space weather and geophysical applications: A review, Russ. J. Earth. Sci., 17, no. 2, p. ES1004, https://doi.org/10.2205/2017ES000597.
Ponomarenko, P.V., B.J. Fraser, F.W. Menk, et al. (2002), Cusp-latitude Pc3 spectra: band-limited and power-law components, Annales Geophysicae, 20, no. 10, p. 1539–1551, https://doi.org/10.5194/angeo-20-1539-2002.
Rodkin, M.V., V.F. Pisarenko (2006), Extreme earthquake disasters: verification of the methods of parameterization of the character of distribution of the rare major events, Advances in Geosciences, 1, p. 75–89, https://doi.org/10.1142/9789812707178_0008.
Russell, C.T., B.K. Fleming (1976), Magnetic pulsations as a probe of the interplanetary magnetic field: A test of the Borok $B$ Index, Journal of Geophysical Research, 81, no. 34, p. 5882–5886, https://doi.org/10.1029/JA081i034p05882.
Soloviev, A., A. Chulliat, S. Bogoutdinov, et al. (2012), Automated recognition of spikes in 1 Hz data recorded at the Easter Island magnetic observatory, Earth Planets and Space, 64, no. 9, p. 743–752, https://doi.org/10.5047/eps.2012.03.004.
Soloviev, A., S. Bogoutdinov, A. Gvishiani, et al. (2013), Mathematical tools for geomagnetic data monitoring and the INTERMAGNET Russian segment, Data Science Journal, 12, p. 114–119, https://doi.org/10.2481/dsj.WDS-019.
Takahashi, K., R.L. McPherron, T. Terasawa (1984), Dependence of the spectrum of Pc 3–4 pulsations on the interplanetary magnetic field, JGR: Space Physics, 89, no. A5, p. 2770-2780, https://doi.org/10.1029/JA089iA05p02770.
Uritsky, V., N. Smirnova, V. Troyan, F. Vallianatos (2004), Dependence of the spectrum of Pc 3–4 pulsations on the interplanetary magnetic field, Physics and Chemistry of the Earth, 29, p. 473–480, https://doi.org/10.1016/j.pce.2003.11.015.
Wolfe, A. (1980), Dependence of mid-latitude hydromagnetic energy spectra on solar wind speed and interplanetary magnetic field direction, JGR: Space Physics, 85, no. A11, p. 5977–5982, https://doi.org/10.1029/JA085iA11p05977.
Vellante, M., U. Villante, M. De Lauretis, G. Barchi (1995), Solar cycle variation of the dominant frequencies of Pc3 geomagnetic pulsations at L = 1.6, Geophysical Research Letters , 23, no. 12, p. 1505–1508, https://doi.org/10.1029/96GL01399.
Yagova, N.V. (2015), Spectral slope of high-latitude geomagnetic disturbances in the frequency range 1–5 mHz. Control parameters inside and outside the magnetosphere, Geomagnetism and Aeronomy, 55, no. 1, p. 32–40, https://doi.org/10.1134/S0016793215010144.
Yagova, N.V., B. Heilig, V.A. Pilipenko, et al. (2017), Nighttime Pc3 pulsations: MM100 and MAGDAS observations, Earth, Planets and Space, 69, no. 61, p. 1–17, https://doi.org/10.1186/s40623-017-0647-x.
Yagova, N.V., V.A. Pilipenko, E.N. Fedorov, et al. (2018), Geomagnetically Induced Currents and Space Weather: Pi3 Pulsations and Extreme Values of Time Derivatives of the Geomagnetic Field's Horizontal Components, Izvestiya, Physics of the Solid Earth, 54, no. 5, p. 749–763, https://doi.org/10.1134/S1069351318050130.
Yumoto, K. (1988), External and Internal Sources of Low-Frequency MHD Waves in the Magnetosphere–A Review, Journal of geomagnetism and geoelectricity, 40, no. 3, p. 293–311, https://doi.org/10.5636/jgg.40.293.
Zelinsky, N.R., N.G. Kleimenova, O.V. Kozyreva, S.M. Agayan, Sh.R. Bogoutdinov, A.A. Soloviev (2014), Algorithm for recognizing Pc3 geomagnetic pulsations in 1-s data from INTERMAGNET equatorial observatories, Izvestiya, Physics of the Solid Earth, 50, no. 2, p. 240–248, https://doi.org/10.1134/S106935131402013X.
Received 11 October 2018; accepted 11 November 2018; published 26 December 2018.


Citation: Bogoutdinov Sh. R., N. V. Yagova, V. A. Pilipenko, S. M. Agayan (2018), A technique for detection of ULF Pc3 waves and their statistical analysis, Russ. J. Earth Sci., 18, ES6006, doi:10.2205/2018ES000646.
Copyright 2018 by the Geophysical Center RAS.