RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 20, ES2001, doi:10.2205/2020ES000704, 2020
Anna A. Skorkina1,2
1IEPT RAS, Moscow, Russia
2GS RAS, Petropavlovsk-Kamchatsky, Russia
The Komandorsky Islands region, tectonically, is unique, being at the junction of the Pacific plate and Bering plate, surrounded by edges of two subduction zones. The tectonic deformation is distributed in the region between a few sub parallel shear faults, of which the Aleutian transform is the most evident. Another one, the Bering fault, was activated again in 2017, when on its section the $Mw 7.8$ earthquake caused a tsunami of limited scale. In this paper for the first time for earthquakes of this region with $M_{L}$ of 3.0–7.0, using more than 500 records of 6 stations equipped by accelerometers, within 300 km from the epicenters, source spectra of S-waves were recovered. The seismic moment and two corner frequencies were determined. Also, the presence of two separate corner frequencies were checked with the spectral ratio method. The estimates of the first, $f_{c1}$, and second, $f_{c2}$, corner frequencies were used to study their scaling properties. We found that $f_{c1}$ scales as $M_{0}^{-0.34\pm0.02}$ what agrees with assumption of source similarity, and $f_{c2}$ scales as $M_{0}^{-0.18\pm0.01}$ what disagrees. In few cases, the third corner frequency of source acceleration spectra were observed.
Earthquakes recordings of the western edge of Aleutian Arc, next to the northern edge of Kurile-Kamchatka subduction zone, differ from ones of neighboring areas. Focal mechanisms gradually changes from thrusts of subduction zones to transform faults near Komandorsky Islands (Bering and Medny Islands), at the boundary of the Pacific and Bering plates. The existence of Bering plate was disputable, however, nowadays the fact is usually accepted [Mackey et al., 1997; Cross and Freymueller, 2008]. The tectonic deformation is distributed in the region between a few sub parallel shear faults, of which the Aleutian transform is the most evident.
 |
| Figure 1 |
 |
| Table 1 |
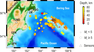
Another such shear fault, the Bering fault, was activated, after December 2003 ($M_{w}^{GCMT}$ 6.6), only in 2016–2017, when in July 2017 on its section with the length of 400 km, the strongest $M_{w}$ 7.8 earthquake [Lay et al., 2017] caused a tsunami of limited scale [Chebrov et al., 2017]. Then, the seismic sources shifted to the west, with strong earthquakes (Table 1) in January 2018 ($M_{w}^{GCMT}$ 6.2) and December 2018 ($M_{w}^{GCMT}$ 7.2). These earthquakes, their aftershock sequences and background seismicity within the region during 2010–2018 (Figure 1) have been recorded at regional hypocentral distances by the digital seismic stations of the Kamchatka Branch of Geophysical Survey, Russian Academy of Sciences.
 |
| Figure 2 |
Traditionally, the earthquakes of this region are classified by the regional magnitude scale based on energy class estimates, within 0.3–4 Hz [Abubakirov et al., 2018] and, additionally, about one third of events (when it is possible) are evaluated via the coda magnitude scale, which characterizes the signal in the frequency range of 0.2–0.5 Hz (Figure 2). In addition, for strongest events there are estimates based on teleseismic recordings. Thus, magnitude estimates given in the Table 1 are compiled from three different sources: $M_{L}$ and $M_{c}$ as well as hypocenters information are from the regional earthquake catalog of Kamchatka (http://emsd.ru), $M_{S}$ are from Geophysical Survey catalog (http:// www.gsras.ru), and $M{w}$ are from Global CMT catalog [Dziewonski et al., 1981; Ekstr{ö}m et al., 2012].
Regularly observed magnitude discrepancies in the region, with discrepancies up to 1.2 magnitude units (Table 1), might be considered as an indicator of complex spectra shape [Duda, 1978], when, for example, the low-frequency part of a spectrum ($M_{c}$, 0.2–0.5 Hz) scales differently than medium-frequency part ($M_{L}$, 0.3–4 Hz). Previously, study on determination of corner frequencies for source spectra of Kamchatka earthquakes revealed that a three-corner frequencies shape is preferred for approximation of source spectra of thrust earthquakes from the Avacha Gulf with $M_{w}$ = 3–6 [Skorkina and Gusev, 2017, Gusev et al., 2017]. The earthquakes from transform faults near the Bering Island were not considered earlier and are of interest in this paper.
One can assume that diversity of source mechanisms in the region should be reflected in source spectra parameters as well. The goal is to determine such additional source parameters as seismic moment ($M_{0}$) and moment magnitude ($M_{w}$) for earthquakes of the region, then, check the scaling properties of two corner frequencies. Also, the magnitude relationships with moment magnitudes are an issue to check.
 |
| Table 2 |
By 2011, several stations of Kamchatka seismic network was upgraded with CMG-5TD accelerometers [Chebrov et al., 2013], including Bering (BKI) set up in 2008, Krutoberegovo (KBG), Ust-Kamchatsk (UK1), Tumrok (TUMD), Gupanovo (GPN) and Shipunskii (SPN) stations (Table 2), closest to the Bering fault (Figure 1). During 2010–2018, when most of the stations have been operated, within 54–56 $^{\circ}$N and 162.5–169.5 $^{\circ}$E, about 500 earthquakes with $M_{L} > $ 4.0 have been recorded. The range of hypocentral distances is from 20 km at the BKI station to 300-400 km at others, the depths are up to 90 km, mainly 30-40 km, and the range of magnitudes $M_{L}$ is 3.5–7.0. Records of more than 240 earthquakes with signal-to-noise ratio $ > 3 $ were processed. Observed multiple events or events well recorded by the only station (BKI) were excluded.
Spectra calculation. Spectra were calculated using a specialized interactive program written in Matlab, the description of which can be found in [Skorkina and Gusev, 2017]. In brief, the program performs visualizing of seismic traces, selecting time windows for signal and noise, implying instrument corrections, estimating of signal-to-noise ratio, calculating Fast Fourier Transform, smooth spectra over bands of 2/3 octave wide, and visualizing of spectra.
Since waveforms of earthquakes near Kamchatka peninsula can look like either strongly scattered signal or with an evident peak, different procedure of choosing the time window length can be considered. To calculate spectra of earthquakes near the Bering Island, we selected the time window length for S-waves within 3–5 sec depending on magnitude and hypocentral distance in order to include the maximum energy of peak-like S-waves and before surface waves arrive. At the next step, frequency-dependent signal-to-noise ratio technique was implied, with noise windows of the same length selected automatically before P-onset. The recordings with SNR $ > 3$, at least within the frequency range of 0.5–10 Hz, where used.
To reduce the observed spectra to the conditions of homogenous media and recover source spectra, we need to evaluate the contributions of such factors as near-surface attenuation and inelastic loss in the media. The $Q$ function was assumed to have the form, following the technique implied earlier to earthquakes of the Avacha Gulf and described in [Skorkina and Gusev, 2017]:
\begin{equation} \tag*{(1)} Q^{-1}(f,r)=Q_{0}^{-1}\cdot(\frac{f}{f_{0}})^{-\gamma}(1+\frac{q(r-r_{0})}{r_{0}}), \end{equation}where $f_{0} = 1$ Hz, $r_{0} = 30$ km, $Q_{0} = 156$, $q = -0.08$; and kappa equals to 0.01 for rock stations (including pyroclastic one) and 0.03 for medium soils, respectively.
 |
| Figure 3 |
 |
| Figure 4 |
Seismic moment and moment magnitude. Using the level of source displacement spectra, one can estimate the seismic moment, and based on seismic moment the moment magnitude [Kanamori, 1977; Hanks and Kanamori, 1979]. This traditional approach uses the theoretical model [Brune, 1970]: the amplitudes are determined based on the ray seismic, and spectral levels on the different rays are averaged, with focal-sphere-averaged radiation pattern for the squared amplitudes of the S-waves. The seismic moment $M_{0}$ (Nm) is estimated by the formula [Hanks and Wyss, 1972]:
\begin{equation} \tag*{(2)} M_{0}=\frac{\Omega_{0} 4\pi \rho r_{0}V_{S}^{3}}{0.63\times2.0}, \end{equation}where $\Omega_{0}$ is the level of the flat spectral segment of the total S-wave displacement vector (m$\cdot$s) reduced to the conditions of an elastic uniform half-space; $\rho$ is the density of the medium (3.3 kg/m$^{3}$); $r_{0}$ is the standard distance (3000 m); $V_{S}$ is the velocity of S-waves (4500 m/s after [Kuzin, 1974]); 0.63 is the focal-sphere root mean square radiation pattern for the S-wave total vector [Boore and Boatwright, 1984]; and 2.0 is coefficient that accounts for the free surface effect.
Using Kanamori's formula [Kanamori, 1977], moment magnitudes can be estimated:
\begin{equation} \tag*{(3)} M_{w}=(2/3)(log_{10}M_{0} [N \cdot m] - 9.1), \end{equation} |
| Figure 5 |
For the period of 2010–2018 there are about 30 estimates of $M_{w}$ obtained by the GCMT agency [Dziewonski et al., 1981; Ekstr{ö}m et al., 2012]. We compared all available estimates of moment magnitudes for earthquakes near the Bering fault (Figure 5). Also, relationships between moment magnitudes and regional magnitude scales ($M_{L}$ and $M_{c}$) have been checked.
 |
| Figure 6 |
Scaling properties of corner frequencies. After obtaining data on seismic moment and two corner frequencies of source spectra, we studied scaling pattern for $f_{c1}$ and $f_{c2}$. The scaling behaviour for $M_{w} > $ 6 is usually close to $f_{c}\sim M_{0}^{-1/3}$ what indicates similarity between source processes of different magnitudes, while for $M < $6 such dependence on seismic moment is controversial. Dependence of the estimates of $f_{c1}$ and $f_{c2}$ on $M_{w}$, obtained for earthquakes of Bering fault and around are presented in Figure 6.
Since one can expect high level of anisotropy around the Aleutian and Bering faults, we checked the existence of two separate corner frequencies by the spectral ratio method, which theory was proposed in [Yokoi and Irikura, 1991] and successfully implemented using observational data in [Imanishi and Ellsworth, 2006]. The key advantage of the method is that all uncertainties caused by media inhomogeneous and respective wave propagation can be neglected because we divide the spectra obtained for hypocenters closely located.
 |
| Figure 7 |
All epicenters of more than 240 earthquakes, with good quality of spectra, were divided by sectors and that epicenters with differences less than 5 degrees of azimuth and 10 km differences were used to obtain spectral ratio. Before dividing, the magnitudes $M_{L}$ were compared, and then, a spectrum of the strongest earthquake was divided by a spectrum of smaller event. The spectral ratio are shown in Figure 7.
The presence of the third corner frequencies or "source-controlled $f_{max}$" of source acceleration spectra also can be seen for ratios between spectra of earthquakes near the Aleutian fault (grey dashed lines in Figure 7), though the closeness to the frequency band limit at high frequencies does not allow answering this question using this data set.
On scaling pattern of corner frequencies. The dependence of the first and second corner frequencies on moment magnitude (related to seismic moment) have been studied. The scaling patterns, $b_{1}$ and $b_{2}$ equal to 0.34 and 0.18. The $b_{2}$ estimate is not within similarity assumption and, moreover, is less than 0.23 as observed for subduction earthquakes near Kamchatka peninsula [Skorkina and Gusev, 2017].
Also, as it can be seen in Figure 7, not all of the spectral ratio shapes indicate the presence of the separate second corner frequency. For example, spectra ratio of 45, 46, 50-52 sectors in Figure 7 are well within the Brune model [Brune, 1970].
This observation can indicate that sources of earthquakes for the region may be interpreted either as from a circular fault (following to the Brune model) or an extended fault (in cases when we clearly see several corner frequencies at source spectra). It can be noted that majority of two-corners source spectra are for earthquakes of the Aleutian fault, while the Bering fault produces many one-corner shapes (Figure 7).
On $M_{w}$-$M_{L}$ and $M_{w}$-$M_{c}$ relationships. Previous magnitude relationships [Abubakirov et al., 2018] revealed stronger differences between levels of magnitudes scales, when \emph{M}$_{w}$ was found to be equal to $M_{L} - 0.4$, while for Bering area it is 0.22. The difference can be interpreted in terms of complex source spectra observed near the Avacha Gulf what has not been considered in calibration curves for regional magnitude, or in terms of medium-frequency (0.3–4 Hz) attenuation which can be higher for subduction earthquakes near the Avacha Gulf, than within interior under the Bering Island.
The relationship between moment magnitude $M_{w}$ and coda magnitude $M_{c}$ revealed less discrepancies what can be explained by a close frequency range used for determining both moment magnitudes and coda magnitudes. Though, stable $M_{c}$ estimates can be obtained only within the range of 4–6 (Figure 5). The estimates for $M_{c} < 4$, compared to the moment magnitudes, look like noise-effected, while estimates for $M_{c} > 6$ look like saturated what is unexpected because the scale was developed for stronger earthquakes.
Another explanation can be based on the peculiar site effect of the "Bering" station [Gusev and Skorkina, 2020] and also the coda pattern observed near the "Bering" station [Lemzikov and Gusev, 1991], when for records of the "Bering" analog seismic station, the increasing of mean coda envelopes were observed at time delays as 100-400 sec. Thus, the scale based on coda estimates without corrections for this effect is unable to classify the earthquakes of the region.
Firstly, using about 500 records of 6 stations equipped by CMG-5TD for earthquakes of 2010–2018 with $M_{L}$ of 3.5–7.0, near the Komandorsky Islands, source spectra of S-waves were recovered, with determining of seismic moment and two corner frequencies.
Secondly, the presence of two separate corner frequencies have been checked with spectral ratio method. Clear evidences for two corner frequencies are shown, while the existence of the third corner of source acceleration spectra cannot be proven with this data set.
Thirdly, more than 240 moment magnitudes have been estimated for the region. Such estimates have been compared to regional magnitudes $M_{L}$ and $M_{c}$.
Fourthly, the estimates of the first and second corner frequencies were used to study their scaling properties, $b_{1}$ equals to 0.34 (with standard deviation of 0.02), and $b_{2}$ is 0.18 (with standard deviation of 0.01) what is not within assumption of similarity.
Abubakirov, I. R., A. A. Gusev, E. M. Guseva, et al. (2018) , Mass determination of moment magnitudes Mw and establishing the relationship between $Mw$ and $ML$ for moderate and small Kamchatka earthquakes, Izvestiya, Physics of the Solid Earth, 54, no. 1, p. 33–47, https://doi.org/10.1134/S1069351318010019.
Boore, D. M., J. Boatwright (1984) , Average body-wave radiation coefficients, Bulletin of the Seismological Society of America, 74, no. 5, p. 1615–1621.
Brune, J. N. (1970) , Tectonic stress and the spectra of seismic shear waves from earthquakes, Journal of geophysical research, 75, no. 26, p. 4997–5009, https://doi.org/10.1029/JB075i026p04997.
Chebrov, V. N., D. V. Droznin, Yu. A. Kugaenko, et al. (2013) , The system of detailed seismological observations in Kamchatka in 2011, Journal of Volcanology and Seismology, 7, no. 1, p. 16–36, https://doi.org/10.1134/S0742046313010028.
Chebrov, V. N., Yu. A. Kugaenko, I. R. Abubakirov, et al. (2017) , The July 17th, 2017 $Mw$=7.8 earthquake on the border of the Komandor seismic gap (western part of the Aleutian Arc), Bulletin of Kamchatka Regional Association "Educational-Scientific Center". Earth Sciences, 35, no. 3, p. 22–25.
Cross, R. S., J. T. Freymueller (2008) , Evidence for and implications of a Bering plate based on geodetic measurements from the Aleutians and western Alaska, Journal of Geophysical Research: Solid Earth, 113, p. B7, https://doi.org/10.1029/2007JB005136.
Duda, S. J. (1978) , Physical significance of the earthquake magnitude: the present state of interpretation of the concept, Tectonophysics, 49, no. 3–4, p. 119–130, https://doi.org/10.1016/0040-1951(78)90161-0.
Dziewonski, A. M., T. A. Chou, J. H. Woodhouse (1981) , Determination of earthquake source parameters from waveform data for studies of global and regional seismicity, Journal of Geophysical Research: Solid Earth, 86, no. B4, p. 2825–2852, https://doi.org/10.1029/JB086iB04p02825.
Ekstr{ö}m, G., M. Nettles, A. M. Dziewo{}ski (2012) , The global CMT project 2004–2010: Centroid-moment tensors for 13,017 earthquakes, Physics of the Earth and Planetary Interiors, 200, p. 1–9, https://doi.org/10.1016/j.pepi.2012.04.002.
Gusev, A. A., A. A. Skorkina (2020) , Empirical spectral characteristics of the media near the seismic strong ground motion stations in Kamchatka, Russian Geology and Geophysics, 61, no. 2, p. 224–233, https://doi.org/10.15372/RGG2019121.
Gusev, A. A., A. A. Skorkina, D. V. Chebrov (2017) , Parameters of source spectra of Mw=3-6 Eastern Kamchatka earthquakes based on shear wave data, Bulletin of Kamchatka Regional Association "Educational-Scientific Center". Earth Sciences, 35, no. 3, p. 36–49.
Hanks, T. C., M. Wyss (1972) , The use of body-wave spectra in the determination of seismic-source parameters, Bulletin of the Seismological Society of America, 62, no. 2, p. 561–589.
Hanks, T. C., H. Kanamori (1979) , A moment magnitude scale, Journal of Geophysical Research: Solid Earth, 84, no. B5, p. 2348–2350, https://doi.org/10.1029/JB084iB05p02348.
Imanishi, K., W. L. Ellsworth (2006) , Source scaling relationships of microearthquakes at Parkfield, CA, determined using the SAFOD pilot hole seismic array, Earthquakes: Radiated Energy and the Physics of Faulting, 170, p. 81–90, https://doi.org/10.1029/170GM10.
Kanamori, H. (1977) , The energy release in great earthquakes, Journal of Geophysical Research, 82, no. 20, p. 2981–2987, https://doi.org/10.1029/JB082i020p02981.
Kuzin, I. P. (1974) , Focal zone and the upper mantle structure in the region of eastern Kamchatka, 131 pp., Nauka, Moscow.
Lay, T., L. Ye, Y. Bai, et al. (2017) , Rupture along 400 km of the Bering fracture zone in the Komandorsky Islands earthquake (MW 7.8) of 17 July 2017, Geophysical Research Letters, 44, no. 24, p. 12,161–12,169, https://doi.org/10.1002/2017GL076148.
Lemzikov, V. K., A. A. Gusev (1991) , Coda-based energy classification of near Kamchatka earthquakes, Journal of Volcanology and Seismology, 11, p. 558–578.
Mackey, K. G., K. Fujita, L. V Gunbina, et al. (1997) , Seismicity of the Bering strait region: evidence for a Bering block, Geology, 25, no. 11, p. 979–982, https://doi.org/10.1130/0091-7613(1997)025%3C0979:SOTBSR%3E2.3.CO;2.
Skorkina, A. A., A. A. Gusev (2017) , Determination of corner frequencies of source spectra for subduction earthquakes in Avacha Gulf (Kamchatka), Russian Geology and Geophysics, 58, no. 7, p. 844–854, https://doi.org/10.1016/j.rgg.2017.06.007.
Yokoi, T., K. Irikura (1991) , Meaning of source controlled fmax in empirical Green function technique based on a T2-scaling law, Annuals of Disaster Prevention Research Institute, Kyoto University, 34, p. 177–189.
Received 5 November 2019; accepted 18 November 2019; published 7 March 2020.


Citation: Skorkina Anna A. (2020), Scaling of two corner frequencies of source spectra for earthquakes of the Bering fault, Russ. J. Earth Sci., 20, ES2001, doi:10.2205/2020ES000704.
Copyright 2020 by the Geophysical Center RAS.