RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 19, ES3003, doi:10.2205/2019ES000664, 2019
I. M. Aleshin1,2, I. V. Malygin1
1Schmidt Institute of Physics of the Earth RAS, Moscow, Russia
2Laverov Federal Center for Integrated Arctic Research RAS, Arkhangelsk, Russia
Inter-well measurements are used to reduce drilling costs with no reduce small kimberlite body detection. The radio wave method enables measurement of the apparent absorption coefficient that is proportional to the effective electrical resistance of the rock. Our point is to build a three-dimensional model of distribution of electrical properties of inter-well space throughout the entire exploration region. The measured data is distributed unevenly because data points are grouped along the linear clusters. The distance between neighbor points composing a cluster is much smaller than distance between clusters. In terms of geostatistics, this means a significant spatial anisotropy of data distribution that is difficult to take into account using standard geostatistical approach. We have shown that the problem could be solved by methods developed within the theory of machine learning. To build a three-dimensional model of attenuation coefficient we used a modified method of $k$-nearest neighbors.
Currently, deposits of diamonds directly accessible from the surface are almost exhausted in the Western Yakutia. Search for kimberlite bodies is carried out in areas where traditional geological and geophysical studies are ineffective [Shmakov, 2017]. For areas covered by sedimentary rocks, as well as traps, the only direct method to search for kimberlites is to run a network of borehole measurements. To reduce the cost of work it is desired to increase the distance between wells. However, this increases the risk of missing small kimberlite pipes. To avoid this, cross-well survey methods are used, in particular, radio wave methods.
The radio wave scanning technique was developed in the middle of the last century (see, for review, [Petrovskij, 1971]) and is being actively used today [Istratov at al., 2006]. This technique is used not only when searching for kimberlite pipes [Tolstov at al., 2018], ore [Kuznetsov, 2008] and oil [Istratov at al., 2000] deposits, etc., but also for natural hazards [Cherepanov, 2017] and technological processes monitoring [Istratov at al., 2009].
 |
| Figure 1 |
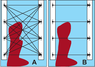
The idea of the method is to estimate the attenuation of an electromagnetic wave as it passes between two wells. The source and receiver of the electromagnetic field is placed in adjacent wells to measure the attenuation of the electric field amplitude. Lower rock resistance corresponds to higher radio wave absorption. Therefore, the absorption coefficient at a fixed frequency is proportional to the electrical conductivity of the medium [Petrovskij, 1971]. There are two kinds of inter-well scanning techniques. First one is named "fan" method shown on panel A of Figure 1. The position of the emitter in the well varies with a given step. At each position, the receiver fixes the amplitude of the electric field emitted by the source. After that, the source moves to the next position. The source also moves throughout the entire working interval of the well. Such a measurement scheme allows to obtain a detailed picture of the electrical properties of the inter-well space in the plane passing through both wells. The joint interpretation of the set of sections obtained in this way allows to obtain a three-dimensional image of the electrical properties of the medium [Kuznetsov, 2012].
If fan survey was chosen $n^{n}$ measurements must be made where $n$ is the number of stops (measurement positions) per well. In practice the survey is often limited to synchronous dipping of the source and receiver in the neighboring wells. In this case, the number of measurements is equal to $n$, which significantly reduces the quantity of measurements, but at the same time the information content of performed measurements also decreases. In fact, such measurement scheme allows us to get only the average value of the apparent attenuation coefficient corresponding to the midpoint of the line connecting the source and receiver positions. Thus the tomographic method becomes inapplicable. To build a three-dimensional model of the medium, we need to use an alternative interpolation procedure. [Aleshin and Zhandalinov, 2009] proposed to construct horizontal sections of the model using kriging [Isaaks and Srivastava,1989]. These parameters should lead to an interpolation error, which is comparable to the accuracy of the input data. However, while constructing a real three-dimensional model, the direct application of the regression methods is impossible because of the extreme anisotropy of the distribution of input data. In addition, even in the two-dimensional case, the solution turns out to be too smooth while our point is to increase image contrast.
One possible alternative is to use machine learning methods. In this case, the interpolation procedure is based on a specific analysis of the source data, which is called training. In machine learning, our task can be classified as the analysis of ordered data. The traditional approach is to build models based on deep neural network architectures, for example, convolutional or recurrent [Nikolenko at al., 2018]. However, the data we have is not enough for quality training of such models. We used the simplest implementation of the $k$-Nearest Neighbors algorithm (abbreviated kNN). This is known as simple but effective method of data analysis. The kNN method belongs to the class of so-called lazy algorithms. Such algorithms do not require a long preliminary training. The decision rules are based on calculating the distances between the data objects [Zhuravlev et al., 2006]. Actually, training is reduced to the calculation of the distance matrix from a given point to all input data.
In this work, we use the data of ALROSA company (http://www.alrosa.ru). Synchronous inter-well radio wave measurement was performed at one of sites in Yakutia. We are unable to use additional data related to the site. Therefore, we restricted our effort to the construction of a three-dimensional model of conductive properties. In later parts, we will discuss only model of spatial distribution of the apparent absorption coefficient of the medium between the wells. To analyze the inter-well measurement data, it is necessary to select a model of the propagation of the electric field emitted by the source. Since our data is obtained from synchronous measurements we can estimate only the average value of the absorption coefficient of the medium along the straight line connecting the source and the receiver. Therefore, we confine ourselves to the simplest model of wave propagation, described by the formula of the radiation field of an electric dipole in a homogeneous isotropic medium
\begin{eqnarray*} E = E_0 \exp(-q/R) / R \sin\theta. \end{eqnarray*}Here, $E$ is the polar component of the electric field, $E_{0}$ is the amplitude of the emitted wave, $R$ is the distance between the source and receiver positions. With synchronous measurements, the source and receiver are placed approximately at the same depth, so the polar angle can be set equal to $\pi/2$. Then the absorption coefficient is
\begin{eqnarray*} q = - \ln \left(RE/E_0\right). \end{eqnarray*}Let $Q=\{q_n\}$ denote the set of input data: the values of the apparent damping factor measured at $N$ points with coordinates $\vec r_n=\{x_{n}, y_{n}, z_{n}\}$. Here, the $x, y$ coordinates determine the position of a point in the horizontal plane, $z$ is the depth measured from sea level. In the kNN algorithm, the value of $q$ at an arbitrary point $\vec r = \{x,y,z\}$ should be calculated by the formula
\begin{equation} \tag*{(1)} q\left(\vec r\right)=\sum_{k=1}^K{w_k\left( \vec r, \vec r_k\right) q_k}, \quad \sum_{k=1}^K w_k = 1, \end{equation}the summation is over $K$ point closest to $\vec r$. The number $K$ is a free parameter of the algorithm (hyperparameter), which requires additional determination. Instead of the number of neighbors, the radius of the sphere with center at the point $\vec r$ is used as the hyperparameter and all points inside the sphere are considered as neighbors. It is natural to choose the Euclidean metric as the distance between points:
\begin{equation} \tag*{(2)} R\left(\vec r_1, \vec r_2 \right) = \sqrt{\left(x_1 - x_2\right)^2+\left(y_1 - y_2\right)^2+\left(z_1 - z_2\right)^2}. \end{equation}The weight function $w_k\left(\vec r, \vec r_k\right)$ depends on the distance between the current point $\vec r$ to the corresponding point with a given value. As a weight function, a value inversely proportional to the distance is usually used:
\begin{eqnarray*} w_k \left(\vec r, \vec r_k\right) \sim 1/R\left(\vec r, \vec r_k \right). \end{eqnarray*}Without taking into account the spatial location of the points of weight are the same for all members of $w_k=1/K$.
 |
| Figure 2 |
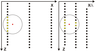
The distribution of data obtained by the radio wave scanning method is strongly anisotropic. The depth step is 5 m with a well length of the order of 500 m while the distance between the nearest wells is approximately 200 m (see Figure 2). We cannot use classical methods of geostatistics [Isaaks and Srivastava, 1989] to build a three-dimensional model of the media. Moreover, the application of the method of nearest neighbors also requires its modification. To reduce the difference in horizontal and vertical scales, we will redefine the metric (2) by entering a dimensionless scale factor $\lambda$:
\begin{equation} \tag*{(3)} R\left(\vec r_1, \vec r_2 \right) = \sqrt{ \left(x_1 - x_2\right)^2 / \lambda^2+ \left(y_1 - y_2\right)^2 /\lambda^2 + \left(z_1 - z_2\right)^2 }. \end{equation}One can expect that a proper choice of the parameter value would allow to compensate for the anisotropy of the data, but we have no criterion for making this choice. Therefore, the scale factor, along with the number of neighbors $K$, is another hyperparameter of the problem. We used the cross-validation to determine the hyperparameters. This approach, along with the hold-out method, is standard in machine learning theory. The source data is divided into $M$ groups ($M=5$), each of these groups is used for testing. In our case, to estimate the quality of the solution, the total rms value of the difference between the deferred values of the observed data, calculated from the remaining data using the formula (1) with the metric (3), is used:
\begin{eqnarray*} \kappa(K,\lambda) = 1/M \sum_{m=1}^M{\kappa^{(m)}(K,\lambda)} \end{eqnarray*} \begin{eqnarray*} \kappa^{(m)} (K,\lambda) = \end{eqnarray*} \begin{eqnarray*} 1 - \sum_{i=1}^{N/M} \left( q_i^{(m)} - q(\vec r_i; K,\lambda) \right)^2 / \sum_{i=1}^{N/M} \left(q_i^{(m)} - \bar q^{(m)}\right)^2 \end{eqnarray*} \begin{eqnarray*} \bar q^{(m)} = \sum_{i=1}^{N/M} q_i^{(m)}. \end{eqnarray*} |
| Figure 3 |
Interpolant $q(\vec r_i; K,\lambda)$ is calculated by the formula (1) using the metric (3) but the holdout data are not taken into account. A coefficient of determination was calculated on a 25 by 25 grid with a unit step for both parameters. The result of the calculations is shown in Figure 3. The coefficient distribution has the shape that is typical for multi-parameter optimization problem. To select the hyperparameter values we have fixed the level 0.7 on the determination coefficient map. It approximately corresponds to the 80-percent correlation between the model and the input data. Intersection of the median of the triangle, which is formed by the coordinate axes and the straight line approximation of the 0.70 level of the determination coefficient to select of the hyperparameter values equal $K=11$ and $\lambda=10$ m.
Since the values of the hyperparameters are determined we can construct the attenuation coefficient image. The calculation of horizontal and vertical cross-sections is implemented in the Python programming language (https://www. python.org) using the Scikit-learn package collection (https://scikit-learn.org).
 |
| Figure 4 |
Figure 4 shows one vertical and two horizontal cross-sections of the model. It can be seen that the model constructed allows to localize objects whose horizontal size are significantly smaller than the distance between the wells. As an example, the areas of high attenuation coefficient values located at a depth of -560 m and horizontal coordinates $X=2950$, $X=4750$ and $X = 5150$ meters can be cited. Their positions are indicated by the corresponding dashed lines on panels A and C, Figure 4.
 |
| Figure 5 |
For clarity, the Figure 5 shows the vertical cross-sections corresponding to these lines, on which the corresponding areas are also clearly visible.
Inter-well synchronous survey data can be used to construct a three-dimensional model of inter-well medium conductivity using the kNN method. The strong anisotropy of the input data can be reduced by modifying the spatial metric, which determines the distance between the data. This can be achieved by introducing a scaling factor that scales in the horizontal direction. The approach used makes it possible to obtain a fairly contrasting image of inhomogeneous areas. In particular, it gives the possibility to make the outlining of areas with linear size smaller than the distance between the wells. The model building process does not depend on the physical model used to interpret the measurement. Refining the model of the physics of wave propagation between wells will improve the quality of image construction without the change in image construction procedure. Of course, the model can be improved by drawing additional data (geological, seismic, magnetic) for their joint interpretation.
Aleshin, I. M., V. M. Zhandalinov (2009), Application of interpolation procedures for presentation of data electromagnetic wave lightning, Russ. J. Earth Sci., 11, no. 1, p. 1–4, https://doi.org/10.2205/2009ES000430.
Cherepanov, A. O. (2017), Multi-frequency radio wave measurements in wells to monitor the process of thawing MMP (example of the Russkoe oil field, Western Siberia), KRAUNZ Bulletin. Series: Earth Science, 4, p. 118–123 (in Russian).
Isaaks, E. H., R. M. Srivastava (1989), Applied Geostatistics, 589 pp., Oxford University Press, New York.
Istratov, V. A., M. G. Lysov, I. V. Chibrikin, et al. (2000), Radio wave geointroscopy (RWGI) of inter-well space in oil fields, Geophysics, Special issue, p. 59–68 (in Russian).
Istratov, V. A., A. V. Skrinnik, S. O. Perekalin (2006), New equipment for radio wave geointoscopy of rocks in the interwell space "RWGI-2005", Instruments and systems for exploration geophysics, no. 1, p. 37–43 (in Russian).
Istratov, V. A., A. V. Kolbenkov, E. V. Perekalin, S. O. Lyax (2009), Radio wave monitoring method of technological processes in the interwell space, KRAUNZ Bulletin. Series: Earth Science, 14, p. 59–68 (in Russian).
Kevorkyanc, S. S., V. Y. Abramov, Y. D. Kovalev (2005), Well radio wave complex for searching for kimberlite pipes in Western Yakutia, Geophysics, 3, p. 56–64 (in Russian).
Kuznetsov, N. M. (2008), Experience of the radiowave geointroscopy of the interwell space for the exploration of a gold-copper deposit, Exploration and protection of mineral resources, no. 12, p. 27–29 (in Russian).
Kuznetsov, N. M. (2012), The 3D method of processing the data of radio wave scanning of the interwell space, KRAUNZ Bulletin. Series: Earth Science, no. 1, p. 240–246 (in Russian).
Nikolenko, S. I., A. A. Kadurin, E. O. Arxangel'skaya (2018), Deep learning, 479 pp., Piter, St. Petersburg (in Russian).
Petrovskij, A. D. (1971), Radio wave methods in underground geophysics, 224 pp., Nedra, Moscow (in Russian).
Tolstov, A. V., N. N. Zinchuk, I. V. Serov (2018), Main results of research and experimental-methodical works of "ALROSA" (PJSC), Efficiency of geological exploration for diamonds: forecasting and resource, methodical, innovative and technological ways to increase it, p. 12–30, "ALROSA" company, Mirny.
Shmakov, I. I. (2018), Problems of scientific support in exploration for diamonds, Geology and minerageny of northern Eurasia. Materials of the meeting dedicated to the 60-th anniversary of the Institute of Geology and Geophysics of the Siberian Branch of the Academy of Sciences of the USSR, p. 265, Sobolev Institute of geology and mineralogy SB RAS, Novosibirsk, Russia (in Russian).
Zhuravlev, Yu. I., V. V. Ryazanov, O. V. Sen'ko (2006), Recognition. Mathematical methods. Software system. Practical applications., 159 pp., Fazis, Moscow (in Russian).
Received 13 April 2019; accepted 16 May 2019; published 22 May 2019.


Citation: Aleshin I. M., I. V. Malygin (2019), Machine learning approach to inter-well radio wave survey data imaging, Russ. J. Earth Sci., 19, ES3003, doi:10.2205/2019ES000664.
Copyright 2019 by the Geophysical Center RAS.