
RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 16, ES6006, doi:10.2205/2016ES000589, 2016
O. I. Parphenuk
Schmidt Institute of Physics of the Earth of the Russian Academy of Sciences (IPE RAS), Moscow, Russia
[1] The study of collision structures is conducted based on the complex model of the thermal and mechanical evolution of overthrusting process for the rheologically layered lithosphere, which includes brittle upper crust and the lower crust and lithospheric upper mantle with different effective viscosity values. Finite element models with Lagrangian approach were used for the problem simulation to study the real deformation and thermal history of orogen. Horizontal shortening leads to the upper crust overthrusting along the fault zone, additional loading to the lower layers which is redistributed in the process of uplift and erosion. This work concentrates on the thermal evolution of collision zones that formed due to upper crust overthrusting movement accompanied by ductile flows at the levels of the lower crust and the upper mantle. The major controls on thermal evolution of the regions with the thickened continental crust are the radiogenic heat supply within the crust, the thermal conductivity of the layers (including its anisotropy in the upper crust) and the rate and time scale of erosion. Calculations of different radiogenic heat content and thermal conductivity in the upper crust lead to the conclusions concerning the time and level of granite melt formation. The horizon of temperatures higher than wet granite solidus appears at the level of 30–40 km, moving upward to the depth 15–20 km at postcollisional stage. The range of maximum temperatures is presented based on the numerical modeling with reliable set of thermal parameters.
Continental collision by overthrusting shows one of the possible ways of the granite melting formation and granitoids exhumation. Collision structures are characterized by the crustal thickening under the orogen uplift, high-grade metamorphic rocks exposed at the surface due to erosion and postcollisional uplift, widespread granite magmatism, complex zone of seismic reflections and high velocities, which results from layering and stratified structure, and marked by positive gravity and aeromagnetic anomalies. These fundamental common features reflect the effect of the main tectonic event – horizontal shortening in compression setting, collision of two continental plates accompanied by the thickening of the crust and the surface uplift and its denudation. Extensive development of horizontal and oblique motions of crustal plates and blocks leads to the disturbances in the thermal regime, heat flow, the surface and Moho topography. The main petrologic mark of such collision is granite melt generated at different depth's levels and exposed at the surface of the terranes and collisional shear zones as a result of the uplift and denudation.
The structure, geometry and evolution of collisional orogens remain a complicated problem of geophysics. In the past years, a great number of important contributions have been made to the understanding of collisional dynamics. Alpinotype collision is characterized by convergence of two continental buoyantly similar plates whose dynamical evolution is governed by the process of overthrusting. The numerical studies of orogenic processes are based on models with different aspects and details of collisional orogens, including constraints from the thermal structure observed in mountain chains by thermobarometric studies [e.g.
Beaumont et al., 2000; Burg and Gerya, 2005; Burov et al., 2001; Faccenda et al., 2008; England, Thompson, 1984; Fernandez et al., 2016; Jammes, Huismans, 2012; Willett et al., 1993].
 |
| Figure 1 |
Precambrian continental shields such as the Anabar, Baltic and Canadian, are the structurally stable areas for at least the last 1.6 Ga. Deeply eroded structures of the shields formed in the process of multistage tectonic evolution including horizontal shortening and collision expose at the surface middle to the lower crustal rocks uplifted along the faults from the depths 20–40 km [Perry et al., 2006; Rosen, Fedorovsky, 2001]. These exposures exhibit asymmetric patterns of metamorphic grade and age across the faults, distinctive Bouguer anomalies reflecting dipping basement structure and often anomalously deep crustal roots. Thermal and deformation structures formed by the crustal thickening and shortening determine to a considerable extent the further evolution of a tectonic unit, subjected to compression. Extension in orogenic zones, defined as horizontal stretching of a lithosphere, that has undergone thickening and shortening, involving perturbations of the lithosphere thermal regime, may be a respond to the increase of vertical stress due to the surface elevation and buoyant roots. There are several examples of compression belts that did not experience lithospheric-scale post-orogenic extension [Mareschal, 1994; Percival, 1990]. A crustal root is preserved beneath the Appalachians, some parts of the Grenville front, under the Kapuskasing structural zone in the Superior Province of the Canadian Shield, the Limpopo belt of Southern Africa, collision belts in the Anabar Shield (Figure 1).
High temperature metamorphism and widespread granite magmatism are common features of many ancient continental collision structures. Deeply eroded areas of the Archean and Proterozoic continental shields formed in the process of tectonic evolution including horizontal shortening and collision expose at the surface middle to the lower crust rocks. This phenomenon seems to be valid also for active collision zones. The massive layer of granite melt approximately of 10 km thickness is observed at 10–15 km depth by seismic methods in the resent orogens such as the Himalayas [Rosen, Fedorovsky, 2001]. The Paleozoic Variscan orogen in Europe is characterized by large volumes of felsic granites intruded during HT-LP metamorphism and exposed in deeply eroded parts of the Variscan belt (the South Bohemian Batholith) [Gerdes et al., 2000].
The main reason for granite melt generation in collision setting is disturbances in the thermal field in the thickened crust. The thermal events and parameters which lead to temperature change at different depths are the following: total radiogenic heat supply within the thickened crust, the thermal conductivity of the layers, non-uniform horizontal heat transfer due to the tectonic deformations, local frictional heating resulting from the movement along the fault, as well as the rate and time scale of uplift erosion.
The continental crust is a repository of long living radioactive elements such as uranium, thorium and potassium. The amount of these elements is a key parameter for the thermal regime of continents and mantle evolution during the process of crust extraction. The estimates of average concentrations of main radiogenic isotopes of $^{235}U$, $^{238}U$, $^{232}Th$ and $^{40}K$ vary by almost a factor of 2. It leads to the estimates of crustal heat production in the range of 0.55–1.31 $\mu$W/m$^3$. Average crustal heat production study for wide set of Precambrian provinces, obtained by systematic surface sampling, leads to a very wide range of surface heat productions 1.01–3.6 $\mu$W/m$^3$ [Jaupart, Mareschal, 2004]. For Archean and Proterozoic provinces of Canada and South Africa radiogenic heat production estimated as 0.6–2.3 $\mu$W/m$^3$ [Jaupart, Mareschal, 1999]. Postcollisional granites generation of Paleozoic age (the Variscan South Bohemian Batholith) 330–370 Ma ago took place in the case of non-uniform distribution of radiogenic heat production with maximum values of 1.9–2.1 $\mu$W/m$^3$ at the depth's interval of 2.6–23.4 km [Gerdes et al., 2000]. In the oldest provinces of Archean age the standard deviation of heat flow density 11 mW/m$^2$ for an average value 41 mW/m$^2$ is large and reflects important variations of crustal composition and heat production in different provinces of the same age [Nyblade, Pollack, 1993]. This is valid for the heat flow variations within the given province.
 |
| Figure 2 |
Measurements of heat production in deep boreholes at Kola (Russia), KTB (Germany) and in Chine did not show systematic variation of heat production with depth. Heat generation in the Archean rocks in the depth interval 8–12 km is higher than in shallower Proterozoic section [The Kola Superdeep, 1998]. The heat production in the 5 km main hole in the Chinese continental scientific drilling program shows increase from $\sim 0.5$ to 1.7 $\mu$W/m$^3$ [He et al., 2008]. At KTB, heat generation is the same at the depths 8–9 km and 1–2 km [Clauser et al., 1997] (Figure 2).
Vertical variation of heat production is not monotonously decreasing (as in widely used exponential law) and cannot be described by a simple function valid everywhere [Jaupart, Mareschal, 2011]. This fact was supported in exposed crustal sections such as the Vredefort in South Africa [Nicolaysen et al., 1981], the Kapuskasing-Wawa [Ashwal et al., 1987] and Pikwitonei-Sachigo areas of Canada [Fountain et al., 1987].
 |
| Table 1 |
Based on detailed crustal heat generation and heat flow data throughout the world the authors [Jaupart, Mareschal, 2004] estimated contribution of three different age continental crust to the heat budget. Heat production of Archean estimated as 0.56–0.73 $\mu$W/m$^3$, 0.73–0.90 $\mu$W/m$^3$ for Proterozoic, and 0.95–1.1 $\mu$W/m$^3$ for Phanerozoic age. Keeping in mind all these facts and conclusions, as well as exponential decay of radioisotopes with age and depletion of the lower crust, we used in our model different constant values of heat generation in tree studied layers, and 1.5 (low), 2.0 (normal), 2.5 (high) $\mu$W/m$^3$ for the upper crust (Table 1). These values are very close to selected in the work of [England, Thompson, 1984] and are in the range of last estimates of heat production values for Canada [Majorowicz, 2016].
The thermal conductivity $\lambda$ ($La$) in the lithosphere is assumed to be independent of temperature and pressure [England, Thompson, 1984]. The summary of the thermal conductivity of crustal materials shows that most conductivity determinations will be in the range 1.5 to 3.5 W/m K [Robertson, 1979], except for the rocks with high content of quartz with higher conductivities. Most silicate minerals are anisotropic and their thermal conductivity depends on direction. Higher conductivity value is measured in direction of foliation with anisotropy coefficient 1.1–1.5 [Jaupart, Mareschal, 2011; Popov et al., 2008]. New data on the thermal conductivity of mantle xenoliths along their long, middle, and short axes also proves that $\lambda$ depends on the shapes of the samples, and these relations can be explained by the dominant orientation of the crystallographic axes of the olivine [Grachev, 2016]. In our model calculations we assumed different constant values of conductivity in tree studied layers and conductivities of the upper crust as 2.0 (low), 2.5 (normal), 3.0 (high) W/m K (Table 1). We also considered a model with increased upper crust conductivity (anisotropy coefficient 1.2) in the direction of main deformation.
Thermal-kinematic model of continental collision calculates pressure, velocity and temperature fields and includes horizontal shortening, brittle overthrusting in the upper crust compensated by the lower crust viscous flow and erosion of the thickened crust. Finite-element 2-D modeling is used to examine the uplift history with surface denudation, post-orogenic stage, the thermal and kinematic conditions for high-temperature metamorphism and the depth, and timing of crustal melting in the case of rheologically layered lithosphere.
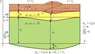 |
| Figure 3 |
The coupled thermal-mechanical model is developed based on mechanical model for overthrusting zones [Parphenuk, 2014; Parphenuk, Mareschal, 1998]. Figure 3 shows the geometry of a two-dimensional model of the lithosphere and boundary conditions used to simulate ductile flow in the lower crust (yellow) and the upper mantle (green) as a result of shortening, loading, and erosion in overthrusting region, as well as thermal evolution in the area including the upper crust (brown). We assume that the rigid upper crust subjected to horizontal shortening and overthrusting is broken by vertical faults into separate blocks weakly connected one with another. Such a rigid but flexible layer can be displaced without contraction and extension. The geometry and uplift algorithm are presented in [Parphenuk, 2014, 2015]. The numerical modeling is thus not concerned with the brittle deformation in the upper crust: the overthrusting and erosion are not included directly in mechanical calculations but are introduced as boundary conditions. In the right upper part of the model, the effect of additional loading due to overthrusting is introduced in the boundary condition by the vertical stress equal to the lithostatic pressure of the overlying material. We assume, that the lower crust and the lithospheric mantle have constant density and behave like linear (Newtonian) fluids with constant effective viscosity ($\rho_1< \rho_2$ and $\mu_1 <\mu_2$).
The equations of momentum and mass conservation for an incompressible Newtonian fluid then describe the ductile flow in the lower crust and lithospheric upper mantle (Figure 3):
\begin{equation} \tag*{(1)} \left\{ \begin{array}{rcl} \mu_i \nabla^2 \mathbf{u} - \nabla P - \rho_i \mathbf{g} =0 \nabla \mathbf{u} =0 \end{array} \right. \end{equation}where $\mathbf g$ is the acceleration of gravity, $P$ is the pressure, $\rho$ – the density, $\mathbf{u} = (u, v)$ is the velocity, $\mu$ – the effective kinematic viscosity. The subscript denotes the material properties of the layer ($i = 1$ corresponds to the lower crust and $i = 2$ to the lithospheric mantle).
Shortening is simulated by a moving vertical left boundary and no-slip condition under the moving brittle upper crust. The horizontal velocity on the upper boundary is the same as that of the moving upper crust left of the fault and it vanishes right of the fault. The normal stress varies horizontally because of the lateral variations in mass of upper crustal material due to the loading redistribution by erosion and sedimentation. The upper crust overlying the ductile region acts as a passive load, and the underlying part of the lithosphere is deflected under the loading; the implicit assumption is that the flexural rigidity of the upper crust is neglected in these calculations. A lithostatic equilibrium condition is assumed at the right boundary. The viscosity of the underlying asthenosphere is considered much lower than that of the lithospheric mantle and a lithostatic equilibrium condition is assumed at the lower boundary
\begin{eqnarray*} \rho_1 g d_1 + \rho_2 g d_2 + \rho_3 g d_3 = \mathrm{const} \end{eqnarray*}The condition of local isostasy compensation at the deeper level than given boundary in asthenosphere with the same density as the lithosphere mantle is approximated by the condition that the normal stress is equal to the lithostatic pressure at that depth without loading:
\begin{eqnarray*} P_3(x) = \rho_3 g h_3 + \rho_1 g h_1 + \rho_2 g (h_2 + h_m) \end{eqnarray*}The Navier-Stokes equations, the incompressibility condition, and the boundary conditions were solved by the finite-element method with Lagrange approach. In these calculations, the nonuniform grid is deformed with time and the nodes thus follow the real deformation history. Some details of the numerical method used are described in [Parphenuk et al., 1994] and numerical method itself is based on the FEM algorithms developed in [Reddy, 1984].
Calculations of velocity and temperature fields presented in this work are based on crustal thickening by overthrusting with dip angle of faulting of $15\mbox{°}$ and shortening duration of 20 Ma with a rate 0.5 cm/yr. Total amount of horizontal shortening is thus 100 km. For the thermal calculations we used the deformation history for effective viscosity of the thickened lower crust $10^{22}$ Pa s, and $10^{23}$ Pa s in the underlying upper mantle. We assume that erosion with a rate of 0.05 cm/yr and concurrent sedimentation start after an additional crustal portion of a substantial thickness is exposed (5 Ma).
The equation of energy conservation is solved for the case of Lagrange coordinates with material time derivative [Turcotte, Shubert, 1985]:
\begin{equation} \tag*{(2)} c_i \rho_i \frac{DT}{Dt} = \lambda_i \nabla^2 T + H_i \end{equation}where $c$ is specific heat, $\rho$ is density, $\lambda$ is the thermal conductivity, and $H$ is the heat generation rate. The thermal calculations are realized on the deformed grid resulted from shortening. The model of thermal evolution thus consists of three layers: 20 km brittle upper crust ($i = 3$ – upper brown layer), 20 km ductile lower crust ($i = 1$, yellow) and 80 km lithospheric mantle ($i = 2$, green) with different thermal, kinematic and rheological parameters (Figure 3). Table 1 lists the values of the basic parameters used for solution of mechanical (1) and thermal
(2) problems. The assumed temperatures at the surface $T_0= 0\mbox{°}$ C and at the bottom $T_1= 1160\mbox{°}$ C are kept constant.
Geological structure of collision zones formed in the processes of shortening, overthrusting and erosion at the level of the upper crust, which are compensated by ductile flows in the lower crust and upper mantle, plays a major role in their thermal evolution. The zones of melting which produce collisional granites essentially result from the geometry and topography due to thrusting [Jaupart, Provost, 1985].
In previous works [Parphenuk, 2014, 2015] the details of mechanical modeling and deformation history of collision belts evolution during and after the convergence process have been compared for main governing parameters: shortening velocity (strain rate), viscosity contrast, erosion rate and dip angle of thrusting. It was shown that the process of denudation (with rates in the range of 0.25–5 mm/yr) has a weak effect on the postcollisional uplift evolution, which is governed mainly by the viscosity values of the lower crust and lithospheric upper mantle as well as initial geometry of the structure. But denudation results in surface exposure of metamorphic sequences, typical for thrust faults.
This work concentrates on the thermal evolution of collision zones that formed due to upper crust overthrust movement. The major controls on thermal evolution of the regions with the thickened continental crust are the radiogenic heat supply within the crust and the thermal conductivity of the layers (including its anisotropy in the upper crust). Calculations of different radiogenic heat content and thermal conductivity in the upper crust lead to the conclusions concerning the time and level of granite melt formation. The thermal model presented here is based on the calculations on the deformed grid as a result of shortening with a rate 0.5 cm/yr for $t = 20$ Ma (total amount of shortening is 100 km), additional loading and denudation of surface uplift for collision process itself and at postcollision stage. The main model parameters are listed in Table 1. The mechanisms of erosion and sedimentation are poorly known, so we assumed a simplified approach to this problem: the high-elevated regions of the uplift are eroded and the material removed is deposited in the lower elevated parts; local erosion with a rate 0.05 cm/yr for the model here starts after time interval 5.0 Ma following the beginning of overthrusting along the fault with the initial dip angle 15°. At postcollision stage the rate of local erosion rate decrease to 0.025 cm/yr. Rocks exposed at the surface will show paleopressures resulted from upthrusting, uplift and erosion. In the model considered metamorphic sequences correspond to erosion level increasing monotonously from about 0.03 km to about 9 km across the thrust fault.
 |
| Figure 4 |
Figure 4 illustrates evolution of the thermal field for the "normal" set of heat production and thermal conductivity. It shows the beginning of deformation process with disturbed thermal regime (a), the final stage of 100-km crustal shortening with a rate of 0.5 cm/yr (b) and the postcollision stage (c). The calculations show the possibility of the partial melting and granite melt generation subjected to the main thermal parameters of the model – the initial temperature distribution, radiogenic heat production and thermal conductivity. The temperature increase can be fairly significant (up to 320° C) at depths level of 10–30 km. In other words, the temperature characteristic of depths of 40–60 km is attained at depths of 20–40 km, creating the conditions for the partial melting and granite melt generation [Parphenuk, 2005, 2012]. This observation confirms the idea of crustal origin of the continental collisional granites [England, Thompson, 1984]. The partial melting zone (wet granite solidus) appears in the thickened crust in the vicinity of thrust fault and widens in the direction of thrusting and upward to the lesser depths. Maximum temperature increase along the fault zone is 300° C. At the deeper lithospheric mantle levels geotherms mainly follow the deformation and are primarily controlled by initial conditions.
 |
| Table 2 |
(Table 2) illustrates total set of models – 9 models – with 3 different heat production values ($H_{\mathrm{low}}$, $H_{\mathrm{norm}}$, $H_{\mathrm{high}}$) and 3 thermal conductivities ($La_{\mathrm{low}}$, $La_{\mathrm{norm}}$, $La_{\mathrm{high}}$). It shows temperatures at the end of shortening (left columns) and 42 Ma after the end of tectonic event (right columns). The depths are $\sim 20$ km (the upper values)–upper–lower crust boundary, and $\sim 30$ km – in the lower crust level under the middle point of the uplift $(\sim 80$ km to the right from the point $x_0$ of Figure 3). Calculations show that these are maximum temperatures in horizontal direction mainly due to the most thickened crust with high heat production rate here. The expected result is that maximum temperature rise is reached in the extreme case of $H_{\mathrm{high}}$ and $La_{\mathrm{low}}$ (the last value is typical mainly for sediments). The heating is about 300° C for the upper crust (initial temperatures in the model are 460° C for upper-lower crust boundary and 610° C in the lower crust). But even in the case of "normal" values of thermophysical parameters (middle of the table) the temperatures at both the final and post-collision stages exceed melting temperature. These results reproduce the main conclusions of 1-D model of [England, Thompson, 1984] although we did not include the total erosion of uptrusted layer. For given set of parameters the range of maximum temperatures attained is 590° C to 750° C from an initial temperature 460° C and 670° C to 88° C from an initial temperature 610° C at the end of shortening (duration is 20 Ma). The further rate of temperature rise for 42 Ma of postcollision evolution is much less (compare with right columns), that demonstrates the importance of the initial phase of heating due to thickening.
 |
| Figure 5 |
 |
| Figure 6 |
Heat flow is the surface manifestation of the processes of thermal field redistribution inside the studied areas. The results of thermal modeling reflected in heat flow evolution are shown in Figure 5 and Figure 6. Thermal conductivity and heat production rate increase lead to practically the same heat flow distribution over the thickened crust at postcollision stage – 42 Ma after termination of shortening (Figure 5). Brocken line in the top figure shows heat flow for the case of anisotropy of thermal conductivity with $\lambda_x = 1.2 \lambda_y$ for "normal" values of parameters. The decrease of vertical heat loss is fairly significant due to heat redistribution in horizontal direction. And as for the case of temperature distribution maximum heat flow values characterize the most thickened crust ($\sim 80$ km to the right from the point $x_0$ of Figure 3).
Figure 6 presents calculations of heat flow evolution over the point with maximum thermal disturbances ($\sim 80$ km to the right from the point $x_0$ of Figure 3) for different heat production rates $H$: 1–1.5 (low), 2–2.0 (normal), 3–2.5 (high) $\mu$W/m$^3$. According to modeling results heat flow value drops by about 10 mW/m$^2$ above the bounding fault during obduction. A physical basis of this phenomenon is that a plate with a certain initial temperature distribution is gradually overthrusted by a layer (in our model, the upper crust) having the same initial temperature, and a "cold" layer is overlain by a "hot" layer. The early postcollision stages are characterized by the significant heat flow increase because of the thickened upper crust layer with maximum heat production. The stable heat flow values are obtained in a time interval compared with thermal conduction time for the crust and kept practically constant due to the very small redistribution of additional load in the course of uplift and local erosion at postcollision stage.
Since the model is predominantly two-dimensional, it can provide insights into the variety of metamorphic conditions in a region that experiences deformations in a horizontal compression setting. 2-D collision model confirms the observation of a wide range of $P- T$ conditions over short distances in metamorphic belts [Chamberlain et al., 1987]. As a result of upward motion along the fault, the additional loading redistribution in the course of erosion, and the viscous compensation at the level of the lower crust, $P - T$ histories will be completely different for the points along the thrust fault. For example, the material is transported from a depth of 20 km to a depth of about 4.5 km while the rocks that were initially located at a depth of 3.5 km will experience a rather complicated $P-T$ evolution [Parphenuk, 2014]. At the postcollision stage (after 20 Ma of shortening) the compressional regime is changed by extension with very low velocities. The very slow uplift and resulting erosion of the upper crust at collisional and postcollisional stages led to a reduced crustal heat production and to the increased strength of the lithosphere. These processes can result in the preservation of the crustal roots for about 2 Ga [Parphenuk et al., 1994, 1998; Perry et al., 2006].
Local effect may result from the frictional heating along the slip zone during the overthrusting. The frictional heat production is proportional to the product of the shear stress across the slip plane, the velocity of obduction and coefficient of friction. The additional heating can raise the temperature by 50–150° C at 10–20 Ma only in the vicinity of slip zone in the case of horizontal shortening rate of $\sim 4$ cm/yr and thrust sheet thickness of 20 km [Brewer, 1981]. This local and moderate additional heating (in comparison with crust thickening effect) is much less in our case of slower thickening, but may initiate partial melting process. If this happens the produced frictional heat sharply lessen. As the relaxation of the local thermal anomalies proceeds rapidly enough, the melting may become a self-limiting process and overthrusting will take place with variable velocity.
The numerical study of collision orogen formed as a result of horizontal shortening of the lithosphere and overthrusting of the upper crust confirm that this thermal-mechanical model with ductile flow in the lower crust can be feasible mechanism, explaining many features of collision belts. Under the assumptions and approximations of the model the calculations show that for geologically reasonable strain rates $ 10^{-15} - 10^{-14}$ s$^{-1}$ combination of 100 km shortening, loading due to overthrusting, erosion and sedimentation lead to the formation of deep crustal roots (by about 10–20 km over a region 100–200 km wide), surface uplift and surface metamorphic sequences, typical for thrust faults.
This work concentrates on the thermal evolution of collision zones that formed due to upper crust overthrusting movement. It was shown that the major controls on thermal evolution of the regions with the thickened continental crust are the radiogenic heat supply within the crust, the thermal conductivity of the layers (including its anisotropy in the upper crust), initial thermal regime, and the rate and time scale of erosion. Calculations of different radiogenic heat content and thermal conductivity in the upper crust lead to the conclusions concerning the time and level of granite melt formation. The horizon of temperatures higher than wet granite solidus appears at the level of 30–40 km, moving upward to the depth 15–20 km at postcollisional stage. The thermal-mechanical model provides the explanation of the possibility of deep crustal sources for granite melting and gives the range of main parameters in the case of initial temperature distribution with the heat flow value in the range of 50–60 mW/m$^2$.
For given set of parameters the range of maximum temperatures attained is 590° C to 750° C from an initial temperature 460° C (the depth of upper-lower crust boundary) and 670° C to 885° C from an initial temperature 610° C (at the depth $\sim 30$ km in the lower crust) at the end of shortening (the duration is 20 Ma). The further rate of temperature rise for 42 Ma of postcollision evolution is much less, that demonstrates the importance of the initial phase of heating due to shortening.
Denudation is the main process in deep crustal rocks exposure, which is observed in wide range of $P - T$ conditions over short distances in metamorphic belts. It also leads to the upward movement of partial melting zone which is observed at 10–15 km depth by seismic methods in young orogens.
The following set of parameters is critical to initiate crustal melting and granite formation: initial temperature distribution with heat flow density value about 60 mW/m$^2$, relatively high radiogenic heat production, slow crustal thickening (0.5–1 cm/yr for 10–20 Ma) and slow exhumation. The results of our thermal modeling confirm other model estimates [England, Thompson, 1984; Gerdes et al., 2000].
Ashwal, L. D., P. Morgan, S. A. Kelley, J. A. Percival (1987), Heat production in an Archean crustal profile and implications for heat flow and mobilization of heat-producing elements, Earth Planet. Sci. Lett., 85, p. 439–450, doi:10.1016/0012-821X(87)90139-7.
Beaumont, C., J. A. Munos, J. Hamilton, P. Fullsack (2000), Factorscontrolling the Alpine evolution of Central Pyrenees inferred from a comparison of observations and geodynamical models, J. Geophy. Res., 105, no. B4, p. 8121–8145, doi:10.1029/1999JB900390.
Brewer, J. (1981), Thermal effects of thrust faulting, Earth Planet. Sci. Lett., 56, p. 233–244, doi:10.1016/0012-821X(81)90130-8.
Burg, J. P., T. V. Gerya (2005), The role of viscous heating in Barrovian metamorphism of collisional orogens: thermomechanical models and application to the Lepontine Dome in the Central Alps, J. Metamorp. Geol., 23, p. 75–95, doi:10.1111/j.1525-1314.2005.00563.x.
Burov, E., L. Jolivet, L. Le Pourhiet, A. Poliakov (2001), A thermomechanical model of exhumation of high pressure (HP) and ultrahigh pressure (UHP) metamorphic rocks in Alpinotype collision belts, Tectonophysics, 342, p. 113–136, doi:10.1016/S0040-1951(01)00158-5.
Chamberlain, C. P., et al. (1987), Influence of deformation on pressure–temperature paths of metamorphism, Geology, 15, p. 42–44, doi:10.1130/0091-7613(1987)15<42:IODOPP>2.0.CO;2.
Clauser, C., P. Gieses, E. Huenges, et al. (1997), The thermal regime of the crystalline continental crust: implications from the KTB, J. Geophys. Res., 102, p. 18,417–18,441, doi:10.1029/96JB03443.
England, P., A. B. Thompson (1984), Pressure–temperature–time paths of regional metamorphism. Part I: Heat transfer during the evolution of regions of thickened continental crust, J. Petrology, 25, p. 894–928, doi:10.1093/petrology/25.4.894.
Faccenda, M., T. V. Gerya, S. Chakraborty (2008), Styles of post-subduction collisional orogeny: Influence of convergence velocity, crustal rheology and radiogenic heat production, Lithos, 103, p. 257–287, doi:10.1016/j.lithos.2007.09.009.
Fernandez, R. D., et al. (2016), Tectonic evolution of Variscan Iberia: Gondwana-Laurussia collision revisited, Earth-Science Reviews, 162, p. 269–292, doi:10.1016/j.earscirev.2016.08.002.
Fountain, D. M., M. H. Salisbury, K. P. Furlong (1987), Heat production and thermal conductivity of rocks from the Pikwitonei-Sashigo continental cross section, central Manitoba: implications for the thermal structure of Archean crust, Can. J. Earth Sci., 24, p. 1583–1594.
Gerdes, A., G. Worner, A. Henk (2000), Post-collisional granite generation and HT-LP metamorphism by radiogenic heating: the Variscan South Bohemian Batholith, J. Geol. Soc., London, 157, p. 577–587, doi:10.1144/jgs.157.3.577.
Grachev, A. F. (2016), Anisotropy of elastic properties and thermal conductivity of the upper mantle – a case study of xenoliths shape: Evidence from xenoliths in basalts in North Eurasia, Russ. J. Earth. Sci., 16, p. ES2002, doi:10.2205/2016ES000566.
He, L., S. Hu, W. Yung, et al. (2008), Heat flow study at the Chinese Scientific Drilling site: Borehole temperature, thermal conductivity, and radiogenic heat production, J. Geophys. Res., 113, p. B02404.
Jammes, S., R. S. Huismans (2012), Structural styles of mountain building: Controls of lithospheric rheologic stratification and extensional inheritance, J. Geophys. Res., 117, p. B10, doi:10.1029/2012JB009376.
Jaupart, C., J.-C. Mareschal (1999), The thermal structure and thickness of continental roots, Lithos, 48, p. 93–114, doi:10.1016/S0024-4937(99)00023-7.
Jaupart, C., J.-C. Mareschal (2004), Constraints on crustal heat flow data, Treatise on Geochemistry, 3: The Crust, R. L. Rudnick (ed.), p. 65–84, Elsevier Sci. Pub., Amsterdam.
Jaupart, C., J.-C. Mareschal (2011), Heat Generation and Transport in the Earth, 464 pp., Cambridge Univ. Press, New York.
Jaupart, C., A. Provost (1985), Heat focusing, granite genesis and inverted metamorphic gradients in continental collision zones, Earth Planet. Sci. Lett., 73, p. 385–397, doi:10.1016/0012-821X(85)90086-X.
Majorowicz, J. A. (2016), Heat flow-heat production relationship not found: what drives heat flow variability of the Western Canadian foreland basin?, Int. J. Earth. Sci. (Geol Rundsch), p. 14, doi:10.1007/s00531-016-1352-x.
Mareschal, J.-C. (1994), Thermal regime and post-orogenic extension in collision belts, Tectonophysics, 238, p. 471–484, doi:10.1016/0040-1951(94)90069-8.
Nicolaysen, L. O., R. J. Hart, N. H. Gale (1981), The Vredefort radioelement profile extended to supracrustal strata at Carletonville, with implications for continental heat flow, J. Geophys. Res., 86, p. 10,653–10,662, doi:10.1029/JB086iB11p10653.
Nyblade, A. A., H. N. Pollack (1993), A global analysis of heat flow from Precambrian terrains: implications for the thermal structure of Archean and Proterozoic lithosphere, J. Geophys. Res., 98, p. 12,207–12,218, doi:10.1029/93jb00521.
Parphenuk, O. I. (2005), Thermal regime of collisional overthrust structures, Izvestiya, Physics of the Solid Earth, 41, no. 3, p. 238–240.
Parphenuk, O. I. (2012), Study of thermal conditions of granite melt formation in collision areas (based on numerical simulation), Monitoring. Science and Technology, no. 3(12), p. 11–20 (in Russian).
Parphenuk, O. I. (2014), Analysis of the collisional uplifts erosion influence on the overthrusted structures and the process of deep crustal rocks exhumation (numerical modeling), Bulletin of Kamchatka regional association Educational-Scientific Center, Earth Sciences, no. 1(23), p. 107–120 (in Russian).
Parphenuk, O. I. (2015), Uplifts formation features in continental collision structures (evolution modeling), Russ. J. Earth. Sci., 15, p. ES4002, doi:10.2205/2015ES000556.
Parphenuk, O. I., J.-C. Mareschal (1998), Numerical modeling of the thermomechanical evolution of the Kapuskasing structural zone, Superior Province, Canadian Shield, Izvestiya, Physics of the Solid Earth, 34, no. 10, p. 805–814.
Parphenuk, O. I., V. Dechoux, J.-C. Mareschal (1994), Finite-element models of evolution for the Kapuskasing structural zone, Can. J. Earth Sci., 31, p. 1227–1234, doi:10.1139/e94-108.
Perchuk, L. L. (1973), Thermodynamic Regime of Deep Petrogenesis, 318 pp., Nauka, Moscow (in Russian).
Percival, J. A. (1990), A field guide through the Kapuskasing uplift, a cross section through the Archean Superior Province, Exposed Cross-Sections of the Continental Crust, NATO ASI Ser., 317, p. 227–283.
Perry, H. K. C., J.-C. Mareschal, C. Jaupart (2006), Variations of strength and localized deformation in cratons: The 1.9 Ga Kapuskasing uplift, Superior Province, Canada, Earth Planet. Sci. Lett., 249, p. 216–228.
Popov, Yu. A., R. A. Romushkevich, D. E. Micklashevsky, et al. (2008), New results of geothermal and petrothermal study of scientific continental boreholes sections, The Earth's Thermal Field and Related Research Methods, p. 208–212, RSGPU Publ., Moscow (in Russian).
Reddy, J. N. (1984), An Introduction to the Finite-Element Method, 459 pp., McGrow-Hill, New York.
Robertson, E. C. (1979), Thermal Conductivities of Rocks, Open-File Report, 79–356 pp., U.S. Geol. Surv., U.S.
Rosen, O. M. (1995), Metamorphic effects of tectonic movements at the low crustal level: Proterozoic collision zones and terranes of the Anabar Shield, Geotectonics, 29, no. 29, p. 91–101.
Rosen, O. M., V. S. Fedorovsky (2001), Collisional Granitoids and the Earth Crust Layering, 188 pp., Nauchnyi Mir, Moscow (in Russian).
The Kola Superdeep, (1998), Scientific Results and Investigations, 260 pp., MFTeckhnoneftegas, Moscow (in Russian).
Turcotte, D., J. Shubert (1985), Geodynamics, Vol. I, 376 pp., Mir, Moscow (translated to Russian).
Willett, S., C. Beaumont, P. Fullsack (1993), Mechanical model for the tectonics of doubly vergent compressional orogens, Geology, 21, p. 371–374, doi:10.1130/0091-7613(1993)021<0371:MMFTTO>2.3.CO;2.
Received 29 November 2016; accepted 3 December 2016; published 14 December 2016.


Citation: Parphenuk O. I. (2016), Thermal regime and heat transfer during the evolution of continental collision structures, Russ. J. Earth Sci., 16, ES6006, doi:10.2205/2016ES000589.
Copyright 2016 by the Geophysical Center RAS.