
RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 16, ES4002, doi:10.2205/2016ES000574, 2016
M. O. Eremin1,2
1National Research State University, Tomsk, Russia
2Institute of Strength Physics and Materials Science SB RAS, Tomsk, Russia
It is shown in the paper that the system of equations of solid mechanics, which has a mixed type, demonstrate the most common features of evolution of nonlinear dynamic systems. Previous investigations of seismic process were carried out on the base of simplified (sand-pile, land-slide) models which gave a graph of recurrence of seismic events and information about the state of self-organized criticality (SOC). However, these simplified models do not contain the information about the stress-strain state of the loaded geomedia and its proximity to the critical state. In the proposed paper the model of rock mass with excavation is constructed and general step of roof caving is modelled. On the base of these modeling the formation of critical state in loaded geomedia is studied. The fluctuations of stress-strain state at different points of geomedia are studied as the reflection of fracture process occurring in the main elements of rock mass: roof and floor, when the coal face is advanced. It is shown that the probability distribution function (PDF) dependencies, amplitude-frequency characteristics reflect the state of the rock mass and might be considered as the fractal characteristics of fracture process within. The evolution of these dependencies shows the dramatic change when the critical state is formed in the rock mass surrounding the underground opening.
The modern methods of geomechanical modeling provide an opportunity for investigating the stress-strain state evolution of rock mass at different horizons of underlying coal seams if the structural, elastic, non-elastic and strength characteristics are taken into account. Then the steps of general and set steps of roof caving could be estimated. The amount of geotechnical problems is rather wide. The majority of investigations are dedicated to the estimations of stress-strain state around the underground tunnels or excavations with analytical [Chanyshev et al., 2014; Demin et al., 2015; Lu and Yang, 2013] and numerical [Kiya et al., 2015; Pardoen et al., 2012; Roatesi, 2010; Yang et al., 2014] solutions of boundary problem. The results of these estimations provide a good information about disintegration of rocks around the excavations and/or tunnels due to plastic deformations. To our mind, the most interesting papers concern the temporal mechanical behavior of rock mass with excavations as soon as it supposes the investigation of stability of development workings, rock mass elements (roof and floor) and the influence of rock pressure manifestation during mining [Khoshboresh, 2013; Nuric et al., 2012; Pavlova et al., 2004; Shabanimashcool, 2012]. The stability and/or development of inelastic strains/fracture around the underground openings is usually considered as the boundary problem of the media with tunnel of circle or other cross-section form subjected to multi-axial loading [Pardoen et al., 2012; Yang et al., 2014; Zhu et al., 2005]. The lack of papers is observed concerning the problem of modeling the excavation at coal face moving [Kwasniewski, 2008; Verma et al., 2013; Wang et al., 2014].
The solution of forecasting problem and risk assessment is actual for the majority of human activities. The problem of forecasting the dangerous manifestations of rock pressure, including the rock bursts, is one of the significant in this range. More widely, this is the problem of forecasting the catastrophic fracture of Earth crust elements, earthquakes and the fracture of any solids and construction's elements. From the theoretical point of view, these problems might be solved with the deep understanding of common laws of evolution of nonlinear dynamic systems since all solids and geomedia are related to such systems. The main goal of studying the evolution of stress-strain state (SSS) in loaded media, as a dynamic system, is the forecast of critical states. The forecasting of both place and time of possible large earthquakes and rock bursts is made empirically on the base of analysis of chosen sequence of earthquakes [Shapoval et al., 2011; Shebalin et al., 2006], and data of monitoring or precursors.
The "sand pile" model is usually used as one of the basic models of geomedia. In the same manner, the large experience of mining and data of geophysical monitoring underlie the forecasting of dangerous dynamic phenomena. The amount of papers dedicated to development of common physical theory of seismic process is increasing continuously. The majority of these theories have the simple equations of nonlinear dynamics as the basis. However, many details of fracture foci formation, as well as seismic process, are not quietly studied. The widely accepted physical model of fracture process doesn't exist. That is why the imitation models became wide spread. They demonstrate several features of real dynamic systems, for example, blow-up regimes, power-law distributions and some other important features of dynamic systems evolution.
The mathematical theory of evolution of loaded solids and media [Makarov, 2008] underlies the methodology for analysis of SSS in rock mass surrounding the excavation. The system of solid mechanics equations composes the core of this theory. The rich history of mechanics demonstrates that these equations model the deformation processes, including the fracture. The numerical solutions of solid mechanics equations demonstrate all known characteristic features of nonlinear dynamic system evolution, if the positive and negative feedbacks and equations of state, characterizing the rate of non-elastic strain and damage accumulation, are included in the system.
In the proposed paper we suppose that the change in fractal characteristics of fracture process might be used as the precursors of critical state formation in rock mass surrounding the underground opening when the coal face is advanced.
The mathematical model include the fundamental conservation laws of continuum mechanics: conservation of mass, impulse:
\begin{eqnarray*} \frac{d\rho}{dt} + \rho \,\mathrm{div} {\mathbf v} =0, \qquad \rho \frac{dv_i}{dt} = \frac{\partial \sigma_{ij}}{ \partial x^j} + \rho F_i \end{eqnarray*}The equation of state (EOS) is taken in the form of isotropic Hookes law and is written in the relaxation form.
\begin{eqnarray*} \dot{\sigma}_{ij} = \lambda (\dot{\theta}^T - \dot{\theta}^P) \delta_{ij} + 2 \mu ( \dot{\varepsilon}_{ij}^T - \dot{\varepsilon}_{ij}^P) \end{eqnarray*}The non-elastic deformation of rock mass elements is descripted within the Drucker-Prager yield function with non-associated flow rule.
\begin{eqnarray*} f(\sigma_{ij}) = \frac{\alpha}{3} I_1 + I_2^{1/2} - Y \end{eqnarray*}The components of inelastic strain rates tensor are defined according to the Nikolaevskii plastic potential.
\begin{eqnarray*} \dot{\varepsilon}_{ij}^p = \left( S_{ij} + \frac{2}{3} \Lambda (Y- \frac{\alpha}{3} I_1) \delta_{ij}\right) \dot{\lambda} \end{eqnarray*}The fracture of the rock mass elements is considered within the theory of damages accumulation.
\begin{eqnarray*} D= \int\limits_{t_0}^t \frac{(\sigma_{\mathrm{cur}} -Y)^2 dt}{\sigma_{*}^2 t_*}, \qquad \sigma_{*} = \sigma_{0*}(1+ \mu_{\sigma}) \end{eqnarray*}Physical-mechanical properties: $\rho$ – material density, $K$ – bulk modulus, $\mu$ – shear modulus, $Y_0$ – initial cohesion, $\alpha$ – coefficient of internal friction, $\Lambda$ – dilation coefficient, $\lambda$ – the first Lame coefficient.
Other parameters of the model: $\mathbf v$ – the velocity vector, $v_i$ – the velocity vector components, $\sigma_{ij}$ – the components of stress tensor, $x^j$ – the Cartesian coordinates, $F_i$ – the components of mass force. $\dot{\theta}^T$ – the rate of total volumetric deformation, $\dot{\theta}^P$ the rate of plastic volumetric deformation, $\dot{\varepsilon}_{ij}^T$ – the components of total strain rate tensor, $\dot{\varepsilon}_{ij}^P$ – the components of plastic strain rate tensor. $I_1$ – the first invariant of stress tensor, $I_2$ – the second invariant of stress tensor, $Y$ – the current value of cohesion, $S_{ij}$ – the components of deviatric stress tensor, $\delta_{ij}$ – delta Kronecker, $\dot{\lambda}$ – the multiplier used in theory of plasticity, $\sigma_{\mathrm{cur}}$ – the current value of stress (combination of first and second invariant of stress tensor) at the point of media, $\mu_{\sigma}$ – the Lode-Nadai coefficient, $t_{*}$, $\sigma_{0*}$ – model parameters characterizing the rate of damage accumulation.
In more details, an applied model is explained in [Makarov et al., 2014].
 |
| Figure 1 |
The geological conditions of coal seams correspond to the flat-dipping formations at different angles. In the investigating case, the depth of the coal horizon is 300 m. On the Figure 1, one can see the stratigraphic column and the corresponding physical-mechanical properties of each layer.
The parameters of the rock mass layers are as follows:
The initial condition is the gravitation stress field. The step of calculation grid is 0.5 m. The mining work is made on the depth of 250 m. Other physical-mechanical parameters are in paper [Eremin et al., 2015].
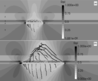 |
| Figure 2 |
Since the Drucker-Prager model is applied in the paper, it is useful to analyze the stress-strain state in terms of relative Coulomb stresses (1) which show the actual state of the media in particular point (Figure 2a and Figure 2b).
\begin{equation} \tag*{(1)} \sigma_c= \frac{\tau}{Y+\alpha P} \end{equation}where $\tau$ – intensity of stresses, $Y$ – current value of cohesion, $P$ – hydrostatic pressure.
 |
| Figure 3 |
If $\sigma_c$ is equal to 1, then the stress-strain state is on the yield surface and non-elastic deformation occurs. The local loss of elastic stability and transition to inelastic state is accompanied with the relaxation of stresses. Such local acts of inelastic deformation might be considered as a small scale catastrophes (or avalanches, in terms of self-organized criticality theory). Each catastrophe produces the stress wave. If we look through the registration of stress fluctuations in several points of rock mass (seismic gauges), than we shall see that the fluctuations reflect the superposition of fracturing of many scales (from micro to macro, Figure 3). These stress waves give information about the current state of the rock mass as the dynamic system.
 |
| Figure 4 |
The PDF-dependency show the dynamic chaos state in the beginning of coal advance, the small scale fractures occur almost independently from each other (Figure 4a). The following changes indicate the transition to self-organized criticality state because of appearance of leading frequency in distribution (Figure 4b), loss of spatio-temporal symmetry of fluctuations and appearance of "fat tails" in statistics of fluctuations (Figure 4c), after the general caving of roof, the distribution rehabilitates the symmetry but doesn't correspond to the initial state (Figure 4d).
 |
| Figure 5 |
 |
| Figure 6 |
The evolution of the amplitude-frequency characteristics (AFC) shows the drastic change of the slope when the critical state is formed in the rock mass (Figure 5 and Figure 6). It occurs when the coalface advancement is close to the step of general caving. For convenience, the Figure 5 shows the AFC for 4 time intervals of the whole range of fluctuations.
The fluctuations of stress-strain state at different points of geomedia are studied as the reflection of fracture process occurring in the main elements of rock mass: roof and floor, when the coal face is advanced. It is shown that the PDF dependencies, amplitude-frequency characteristics reflect the state of the rock mass and might be considered as the fractal characteristics of fracture process within. The evolution of these dependencies shows the dramatic change when the critical state is formed in the rock mass surrounding the underground opening. Particularly, the slope of amplitude-frequency characteristic drops dramatically when the length of mined space gets close to the step of general caving.
The results of numerical modeling show that the developed model, applied for simulation of stress-strain state evolution over the mined space demonstrate all known characteristic features of nonlinear dynamic system evolution.
Chanyshev, A. I., I. M. Abdulin (2014), Stress-strain state of enclosing rock mass around an arbitrary cross-section excavation by measurement of displacements of the excavation walls, Journal of Mining Science, 50, p. 18–24, doi:10.1134/S1062739114010037.
Demin, V. F., N. A. Nemova, T. V. Demina (2015), Analytical modeling of geomechanical processes in the marginal array mining, Journal of Siberian Federal University. Engineering and Technologies, 1, p. 74–97.
Eremin, M. O., et al. (2015), Modelling of processes of damage accumulation and multiscale fracture in rock mass with excavations at mining, AIP Conference proceedings 1683, 020048-1-4, p. 1–4, AIP Publishing, New York, doi:10.1063/1.4932738.
Khoshboresh, A. R. (2013), Memoire, 155 pp., University LAVAL, Canada.
Kiya, O. E., V. Hosseinitoudeshki (2015), The three dimensional strain in cylindrical tunnels, WALIA Journal, 31, p. 172–174.
Kwasniewski, M. (2008), Numerical analysis of strata behavior in the vicinity of a longwall panel in a coal seam mined with roof caving, Continuum and Distinct Element Numerical Modelling in Geo-Engineering, Paper: 07-08, p. 1–12, Itasca, Minneapollis.
Lu, Y., W. Yang (2013), Analytical solutions of stress and displacement in strain softening rock mass around a newly formed cavity, Journal of Central South University, 20, p. 1397–1404, doi:10.1007/s11771-013-1627-3.
Makarov, P. (2008), Mathematical theory of evolution of loaded solids and media, Physical Mesomechanics, 11, p. 19–35, doi:10.1016/j.physme.2008.11.002.
Makarov, P. V., M. O. Eremin, Yu. A. Kostandov (2014), Mathematical theory of evolution of loaded solids and media. Physical mesomechanics, Physical Mesomechanics, 17, p. 199–203, doi:10.1134/S1029959914030047.
Nuric, A., S. Nuric, L. Kricak, I. Lapandic, R. Husagic (2012), Numerical modeling and computer simulation of ground movement above underground mine, World Academy of Science, Engineering and Technology, 6, p. 316–324.
Pardoen, B., F. Collin, S. Levasseur, R. Charlier (2012), Modelling the excavation damaged zone in Callovo-Oxfordian claystone with strain localization, ALERT Workshop, p. 1–23, Univerite de Liege Publishing, Aussois.
Pavlova, L. D., V. N. Fryanov (2004), Modelling of cyclic collapse of rocks at mining with sequential damage accumulation, Izvestiya Tomskogo Politechnicheskogo Universiteta, 307, p. 76–79 (in Russian).
Roatesi, S. (2010), Analysis of the successive phases of a tunnel excavation with support mounting, Proceedings of the Romanian academy, Series A, 11, p. 11–18.
Shabanimashcool, M. (2012), Numerical modeling of the longwall mining and the stress state in Svea Nord Coal Mine, Ph.D. thesis, Norwegian University of Science and Technology, Trondheim, Norway.
Shapoval, A. B., M. G. Sniirman (2011), Universality of algorithmic prognosis of extremal events in time series, Information Technologies and Calculation Systems, 4, p. 58–65 (in Russian).
Shebalin, P., V. I. Keilis-Borok, A. Gabrielov, L. Zaliapin, D. Turcotte (2006), Short-term earthquake prediction by reverse analysis of lithosphere dynamics, Tectonophysics, 413, p. 63–75, doi:10.1016/j.tecto.2005.10.033.
Verma, A. K., D. Deb (2013), Numerical analysis of interaction between hydraulic-powered support and surrounding rock strata, International Journal of Geomechanics, 13, p. 181–192, doi:10.1061/(ASCE)GM.1943-5622.0000190.
Wang, G., H. Y. Wang, Q. M. Huang, C. Q. Su (2014), Numerical modeling of rock cross-cut coal uncovering based on ANSYS, Computer Modelling and New Technologies, 18, p. 26–32.
Yang, H. Q., Y. Y. Zeng, Y. F. Lan, X. P. Zhou (2014), Analysis of the excavation damaged zone around a tunnel accounting for geostress and unloading, International Journal of Rock Mechanics and Mining Sciences, 69, p. 59–66, doi:10.1016/j.ijrmms.2014.03.003.
Zhu, W. C., J. Liu, C. A. Tang, X. D. Zhao, B. H. Brady (2005), Simulation of progressive fracturing processes around underground excavations under biaxial compression, Tunneling and Underground Techn., 20, p. 231–247, doi:10.1016/j.tust.2004.08.008.
Received 13 September 2016; accepted 13 September 2016; published 25 September 2016.


Citation: Eremin M. O. (2016), Fractal characteristics of seismic process in rock mass at mining: Mathematical modeling and analysis, Russ. J. Earth Sci., 16, ES4002, doi:10.2205/2016ES000574.
Copyright 2016 by the Geophysical Center RAS.