RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 12, ES4002, doi:10.2205/2012ES000517, 2012
Experimental investigation of near-surface small-scale structures at water–air interface: Background Oriented Schlieren and thermal imaging of water surface
Yu. Yu. Plaksina1, A. V. Uvarov1, N. A. Vinnichenko1, V. B. Lapshin1,2
1Faculty of Physics, Lomonosov Moscow State University, Moscow, Russia
2Fedorov Institute for Applied Geophysics, Moscow, Russia
Introduction
Abstract
Constructing models of global heat exchange between the ocean and atmosphere requires information on boundary conditions at water–air interface. Experimental and theoretical studies of near-surface structures both in laboratory and in situ have been a part of geophysics for decades. Nowadays usage of modern CFD methods can be complemented by state-of-art experimental techniques providing visualization of small-scale phenomena. Temperature distributions near the liquid–gas interface for various evaporation regimes are measured in laboratory by Background Oriented Schlieren (BOS) and IR thermal imaging of the surface. The results, obtained by these two methods, are shown to coincide with accuracy about 0.1 K. Thanks to simplicity of experimental realization, both methods can be used also in situ. Thermal imaging yields not only the surface temperature field, but also the velocity gradient near the surface. It is shown to be much larger than vorticity of the bulk convective vortices. Possible separate numerical modeling of hydrodynamic processes in liquid and gas making use of thermal imaging data is discussed.
Introduction
Thin layer of water and air adjacent to the interface has structure, totally different from that of the remaining part of atmosphere or ocean. Fluid velocity, temperature, water vapor concentration vary drastically inside this layer. Hence, all dissipative processes: viscosity, thermal conductivity and diffusion – are important. The thickness of this layer (from 0.1 mm to several millimeters) is incomparable with typical geophysical scales. Nevertheless, describing this layer is essential for constructing the whole model, since it is there where all heat and mass exchange between ocean and atmosphere takes place. Small-scale structures of this layer can play an important role in energy transport and dissipation of large-scale flows.
Liquid temperature measurements near the liquid–gas interface present serious experimental challenge. Average vertical temperature profile can be approximated by simple exponential fit [Katsaros et al., 1977; Fedorov and Ginsburg, 1992]
\begin{eqnarray*}
T(z)=T_{bulk}+(T_s-T_{bulk})\exp{\left(-\frac{z}{\delta}\right)},
\end{eqnarray*}
where $T_s$ is the surface temperature of liquid, $T_{bulk}$ is liquid temperature far from the surface and $z$ is the depth. This profile is governed by two parameters: temperature difference $T_{bulk}-T_s$ and surface layer thickness $\delta$. Major experimental difficulties arise from the fact that $T_{bulk}-T_s$ is usually of order 0.1 K and $\delta$ is about 1 mm. This suggests temperature gradients of several hundred K/m and thermal fluxes $\sim10^2\mbox{W/m}^2$. There are two groups of experimental techniques. Methods of the first group allow measuring average values for $\delta$ and $T_{bulk}-T_s$. Temperature difference can be found e.g. by simultaneous thermocouple and thermal imaging measurements [Minnett et al., 2011], and layer thickness is estimated from the total heat flux. Total heat flux is interpreted as molecular one
\begin{eqnarray*}
Q_{total}=-\lambda\,\left.\frac{dT}{dz}\right|_{z=0}=-\frac{T_s-T_{bulk}}{\delta}.
\end{eqnarray*}
Thus, layer thickness can be found if the total heat flux is known. In laboratory it can be determined from standard thermophysical measurements of liquid sample cooling, or from evaporation rate. In natural conditions small containers are immersed into water reservoir and evaporation rate is measured, or profiler thermoprobes of various types are used [Katsaros et al., 1977; Khundzhua et al., 1997]. Bulk formulae, relating heat fluxes to temperature and humidity values at various heights, have been elaborated both for laboratory [Luikov, 1966; Shah, 2003] and in situ measurements [Liu et al., 1979; Gulev and Belgaev, 2012]. These relations allow finding estimates for all heat fluxes constituting the total flux.
It is obvious that non-uniformity of the cold skin in horizontal plane, which is not taken into account by one-dimensional models, is of principal importance because it provides torque for the vortices approaching the surface. More information is required both for deeper understanding of hydrodynamical processes under the liquid–gas interface and for verification of state-of-art numerical codes. Consider the second group of methods, which allow obtaining detailed information about the fields of temperature and other quantities. These are: shadowgraphy [Spangenberg and Rowland, 1961], BOS [Meier, 2002], Particle Image Velocimetry (PIV) performed both in gas and liquid [Volino and Smith, 1999; Bukhari and Siddiqui, 2006, 2008], Laser Induced Fluorescence (LIF) [Bukhari and Siddiqui, 2011], and IR thermal imaging of temperature field at the surface [McAlister and McLeish, 1970; Volino and Smith, 1999; Carlomagno and Cardone, 2010; Ivanitskii et al., 2005]. Principal drawbacks of these methods are well-known. Shadowgraphy requires relatively complex adjustment of experimental setup, thick parallel beams have to be formed. Nevertheless, it was shadowgraphy to give first hint on complex structure of surface layer [Spangenberg and Rowland, 1961]. Background Oriented Schlieren lacks spatial resolution and yields distribution, averaged over line-of-sight [Meier, 2002]. PIV also lacks resolution in vertical direction near the surface, and LIF suffers from concentration gradient of emitting particles in the surface layer, which is observationally equivalent to temperature gradient. IR thermal imaging is becoming, with the development of more sensitive devices, one of the major methods of measurement, but it observes only very thin layer near the surface. Combined usage of PIV and thermal imaging has led to conclusion about complex structure of the flow in upper layer of liquid. It appeared that cold liquid filaments at the surface do not coincide with places of downward vortical motion [Volino and Smith, 1999].
Consider once more profiler thermoprobes [Katsaros et al., 1977; Khundzhua et al., 1997]. Originally, they were used to obtain averaged profiles under laboratory and natural conditions. Actually, their readings correspond to instantaneous values of temperature and can be used for verification of numerical simulation. However, certain difficulties arise, as for any contact method, with interpretation of the results, due to large response time of thermocouples and surface tension influence when the probe enters the liquid. In particular, we have shown that at high probe velocities, typical for in situ measurements, temperature distribution can be significantly distorted due to delayed response of thermocouple in gas. In laboratory it is possible, by decreasing the probe velocity and changing the sensor geometry, to obtain reliable temperature profiles both for gas and liquid. Only the upper liquid layer with thickness about 0.1 mm, geometry of which is violated by the probe during the entry, remains a blank spot.
Temperature field measurements can shed some light on the structure of surface layer. In particular, they can clarify the question whether Marangoni convection takes place near the surface in different liquids, which was widely debated in literature (see e.g. [Fedorov and Ginsburg, 1992]). Shadowgraphy has shown that Marangoni convection is observed in ethanol, but not in water. Modern thermographical methods help to explain this discrepancy. It appears that there are actually two configurations of surface layer, both associated with Marangoni effect i.e. with temperature dependence of surface tension. Classical Marangoni convection takes place in ethanol whereas a system of cold liquid filaments is observed at water surface [Spangenberg and Rowland, 1961; Volino and Smith, 1999].
Experimental techniques
IR thermal imaging
 |
| Figure 1 |
Different regimes of near-surface convection are observed in the present study for various liquids with different thermophysical properties (water, decane, kerosene, glycerine, ethanol and butanol). Network of cold filaments associated with Marangoni convection is typically observed in ethanol, but neither in water, nor in glycerine or kerosene, where motionless cool skin layer is formed [Fedorov and Ginsburg, 1992]. Decane and butanol have been reported to exhibit both kinds of behavior. Usually this is attributed to presence of surfactants e.g. in water. However, our experiments with these liquids revealed that surface layer configuration is determined by initial thermal state and evaporation rate, not by the substance. The results are presented for water, ethanol and butanol. Measurements were performed with FLIR SC7000-M IR thermal imaging device. Image resolution is $640\times 512$ pix, wavelength range is 2.5–5.5 $\mu$m. Camera sensor temperature is 80 K. Figure 1 shows measured surface temperature fields for cooling of initially hot butanol. Conditions for evaporation are changing during the process, so does the surface layer configuration. Two configurations of surface layer are possible: thermocapillary convection and thermocapillary film, characterized by larger cells of hot liquid surrounded by cold filaments and by motionless state of near-surface layer (see below). Both configurations are related to surface tension dependence on temperature. Its role for laboratory and geophysical experiments was discussed e.g. by Lapshin [1990].
Knowing the temperature field, one can obtain information about velocity gradients near the surface. They are related to surface tension by common expression
\begin{equation}
\tag*{(1)}\label{1} \frac{\partial v_x}{\partial z}= \frac{1}{\mu}\frac{\partial\sigma}{\partial T}\frac{\partial T}{\partial x},\qquad \frac{\partial v_y}{\partial z}= \frac{1}{\mu}\frac{\partial\sigma}{\partial T}\frac{\partial T}{\partial y},
\end{equation}
 |
| Figure 2 |
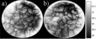
where $\mu$ is dynamic viscosity and $\sigma$ is surface tension. The right-hand side ((1)) is known from experiment. Typically, for water it is about 10 $\mbox{s}^{-1}$. Expanding the velocity gradient as $\partial v_{x, y}/\partial z\sim\Delta v/\delta_1$ and making use of typical velocity values, observed in PIV or numerical simulations ($\Delta v\sim v_{max}\sim10^{-3}$ m/s), one arrives to an estimate for velocity boundary thickness $\delta_1$ about 100 $\mu$m. Bulk convective vortices are characterized by the same velocity difference, but their size is comparable with the tank size, i.e. the vorticity is at least two orders of magnitude less. Near-surface layer exhibits sudden velocity drop, which can be observed by thermal imaging. Figure 2 presents two frames from video record for water surface temperature field with floating powdered coal (also, talc particles were used).
Video record shows that in hot water (with temperature about 50° C) cold fluid filaments below the surface move with velocity about 1 mm/s, whereas average velocity of coal particles at the surface is an order of magnitude less (0.1 mm/s). Since IR radiation comes from depths not more than 100 $\mu$m, a conclusion can be derived that velocity gradient below the surface is very large indeed. This velocity gradient prevents bulk convective vortices from reaching the surface, which implies complex structure of surface layer with vortices of several scales located above each other. Same conclusion was made in [Volino and Smith, 1999] from comparison of thermography data with PIV.
Thermal imaging allows separating the problem of hydrodynamical simulations in liquid and gas. Instead of solving equations for both media and coupling the solutions by setting equal temperatures and heat fluxes at the interface [Nunez and Sparrow, 1988], one can solve two separate problems using thermal imaging data as boundary condition at the liquid surface. Then, heat fluxes can be compared. Simulations in water should also take into account conditions ((1)), determining velocity gradient at the surface. Boundary conditions for the air-side problem are completely specified too: temperature and humidity (which can be taken equal to saturated value for given temperature) at the surface are known, as well as gas temperature and humidity far from the surface, measured by simple probes.
Background Oriented Schlieren
Major drawback of thermography is small thickness of the observable layer. Hence, it is worthwhile to complement thermography with some technique providing data on spatial structure of temperature distribution at considerable depths. In present investigation BOS method is implemented, which is relatively new and has not been used for evaporation studies before. Actually, original scheme of observations by Spangenberg and Rowland [1961] is used, involving top view and side view, but top view is obtained with thermal imaging and side view is provided by BOS, instead of shadowgraphy. These substitutions increase greatly the obtained images quality and allow comparison of the results for two independent experimental techniques. Thus, accuracy can be estimated. Moreover, thanks to simplicity of experimental realization of both methods, they can be applied for various problems both for laboratory and in situ measurements.
 |
| Figure 3 |
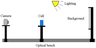
BOS technique, proposed by Meier [2002], is extremely simple in realization. Variations of refraction index inside investigated transparent object are measured by digital comparison of two photographs of a background pattern. First photograph (reference image) is taken under constant refraction index conditions and the second one (distorted image) – through the object being investigated. For evaporation of liquid in tank reference image can be taken with the tank lid on, thereby eliminating evaporation and correspondent heat fluxes. Refraction results in rays deflection and apparent displacement of background pattern elements. Ray path is described by vector function $\vec{R}(S)$ (Figure 3), which is orthogonal to isosurfaces of the wave phase $\Psi$. Total ray deflection is related to the angle $\alpha$ between the tangent line drawn in the end point of the path and the original ray direction. For small deflections $\alpha\approx\tan\alpha=dR_x/dR_z\approx dR_x/dS$. $\vec{R}(S)$ can be found from the following equations [Born and Wolf, 1980]
\begin{equation}
\tag*{(2)}\label{2} \frac{d\vec{R}}{dS}=\vec{l},\quad \frac{\partial\left( n\vec{l}\,\right)}{\partial S}=grad\,n,\quad \frac{\partial\Psi}{\partial S}=n,
\end{equation}
where $n$ is refraction index. For $n=const$ first two equations of the set ((2)) yield linear $\vec{R}(S)$ i.e. straight-line propagation of the light. If refraction index variations are present, total deflection angle is
\begin{eqnarray*}
\alpha=\frac{1}{n_0}\int\limits_H\frac{\partial n}{\partial x}\,dz,
\end{eqnarray*}
 |
| Figure 4 |
 |
| Figure 5 |
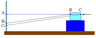
and integration is performed along line-of-sight. For typical layout of BOS setup (Figure 4) object size along line-of-sight (width of the tank) is small in comparison with distance from object to camera. In this case the deflection angle is practically independent from the position along line-of-sight, at which refraction index is varied. For example, total displacements $AB_1$ and $AC_1$, shown in Figure 5, are similar if $BC\ll AB$. This allows obtaining 2D refraction index fields, averaged over the third coordinate. Exact position of the point, where the ray leaves the tank, does not influence on the displacement value if tank walls are flat. Otherwise, e.g. for cylindrical tanks deflection angle depends on inhomogeneity position inside the tank and multiangle tomographical reconstruction is required. The displacement field can be determined by cross-correlation interrogation of the recorded images, also employed in PIV. Multi-pass algorithm with discrete window offset [Scarano and Riethmuller, 1999] is used with little modifications. Optical considerations lead to the following Poisson equation for the refraction index field [Vinnichenko et al., 2011]
\begin{equation}
\tag*{(3)}\label{3} \frac{\partial^2 n}{\partial x^2}+\frac{\partial^2 n}{\partial y^2}=\frac{2 a}{h(2L+h)}\left(\frac{\partial \xi_x}{\partial x}+\frac{\partial \xi_y}{\partial y}\right),
\end{equation}
where $a$ is one pixel size in background plane, $\vec{\xi}$ is the displacement vector field measured in pixels, $h$ is the tank width and $L$ is the distance from background to tank. Since pressure variations in small water tanks are negligible, refraction index is a function of density and temperature. Hence, temperature field can be obtained by solving two algebraic equations: empirical equation of state and Lorentz-Lorenz relation for refraction index.
 |
| Figure 6 |
Two types of background patterns were used in the experiments: irregular dotted pattern (Figure 6a) and wavelet-noise pattern (Figure 6b), proposed by Atcheson et al. {2009]. Dot size in irregular dotted pattern was adjusted for the prescribed distances between the background, water tank and the lens, so that dot image size was about 2–3 pix, which is optimal for cross-correlation interrogation. In contrast, wavelet-noise pattern can be used as universal background for different relative positioning of BOS setup parts, since it contains details of various size. However, it yields slightly larger errors than dotted pattern and is more vulnerable to image blur [Vinnichenko et al., 2012]. Most of the results were obtained with irregular dotted pattern.
Accuracy of the measurements can be estimated by cross-correlating two reference images. This estimate takes into account the errors of cross-correlation algorithm, lens aberrations, noise of the camera sensor and possible camera displacement. Also, it accounts for refraction index fluctuations which are present even without evaporation. It does not take into account distorted image blur caused by nonlinear refraction index variations [Vinnichenko et al., 2012]. In all cases the estimated error of temperature measurements was of order 0.01 K. Note that this error is for temperature variations only. In order to determine absolute temperature value, one has to specify temperature in some point. In our experiments, bulk liquid temperature was measured by thermocouple with accuracy 0.1 K. Refraction index value correspondent to this temperature and atmospheric pressure was used as boundary condition for ((3)) at lower boundary. Temperature and relative humidity of the air, which determine the evaporation intensity, were measured by another thermocouple and TESTO-650 gauge.
Results and discussion
 |
| Figure 7 |
As discussed above, temperature measurements in the upper layer with thickness about 1 mm are extremely challenging. Figure 7c shows the results obtained by two methods at the water surface. Temperature field obtained by thermal imaging was averaged over the tank width and compared to BOS results at the upper boundary of the domain (intrinsically averaged over BOS line-of-sight). Note that
BOS images were cropped below liquid surface in order to avoid the errors associated with meniscus and multiple reflections of light from the interface. Water tank dimensions are $30\times50\times19$ mm. The agreement is very good. Use of two different methods justifies the validity of obtained experimental results, making evaporation from a small water tank a good test case for numerical models involving evaporation. BOS temperature is slightly higher, indicating that the upper sublayer about 0.1 mm is not well resolved or is possibly lost during the image crop. However, the difference between two distributions is about 0.05 K, less than accuracy of thermocouple providing the reference temperature value for BOS measurements. Good agreement is related to geometry of the considered flow, which is nearly 2D. If cold filaments are observed near the liquid surface, the complete structure of temperature field is not captured by BOS, since it yields temperature values averaged over line-of-sight. Nevertheless, combination of BOS side view and thermal imaging of the surface gives notion about thermal structures in the considered flow.
 |
| Figure 8 |
 |
| Figure 9 |
Evaporation is much more intense in ethanol. The dependence of refraction index on temperature is stronger than in water, hence BOS sensitivity in ethanol is higher. Thermal imaging indicates presence of a network of cold filaments at the surface and an area of cold liquid sinking down in central part of the tank. Results of simultaneous measurements by thermal imaging and BOS are demonstrated in Figure 8. Comparison of temperature distributions along the interface, averaged over the tank width, is presented in Figure 9. The agreement is reasonably good. Maximal deviation is less than 0.08 K. Some disagreement in positions of local maxima and minima can be associated both with thermal structure changes in the upper liquid layer and BOS method accuracy. Vortical motion, coming from the surface, engulfs also the deeper layers. Hence, even though BOS can not resolve the layer immediately adjacent to the surface, it can provide valuable data on the emerging thermal structures.
 |
| Figure 10 |
 |
| Figure 11 |
Experiments were also performed for a larger tank ($31\times16\times25$ cm) filled with water. The Rayleigh number is increased about 1000 times in comparison with the case shown in Figure 7 and Figure 8 and convection becomes turbulent (see Figure 10). BOS results are averaged over much longer distance, so the temperature fluctuations with respect to average value are small. Correspondent temperature profiles along the interface are displayed in Figure 11.
Conclusions
- BOS method is very promising for investigations of thermal structures near gas–liquid interface. Its accuracy is generally better than 0.1 K. Simplicity of experimental realization allows using it for in situ measurements.
- Combination of BOS with IR thermal imaging provides reliable data on the entire structure of thermal field. Also, boundary conditions for velocity and temperature at the interface can be obtained, making separate modeling of problem in liquid and gas feasible.
- Two configurations of the near-surface layer were observed for various liquids and conditions, both associated with Marangoni convection. Velocity gradients near the interface are shown to be much larger than vorticity of Rayleigh convection vortices in bulk liquid. This implies complex multi-layered vortical structure of the upper liquid layer.
Acknowledgment
This work was partially supported by Russian Foundation for Basic Research (grant 12-08-01077-a).
References
Atcheson, B., W. Heidrich, and I. Ihrke (2009), An evaluation of optical flow algorithms for background oriented schlieren imaging, Exp. Fluids, 46, 3, 467–476, doi:10.1007/s00348-008-0572-7.
Born, M., E. Wolf (1980), Principles of Optics, Pergamon, New York, 808 pp.
Bukhari, S. J. K., M. H. K. Siddiqui (2006), Turbulent structure beneath air-water interface during natural convection, Phys. Fluids, 18, 3, 035106, doi:10.1063/1.2185709.
Bukhari, S. J. K., M. H. K. Siddiqui (2008), An experimental study of the airside flow structure during natural convection, Phys. Fluids, 20, 12, 122103, doi:10.1063/1.3054153.
Bukhari, S. J. K., M. H. K. Siddiqui (2011), The structure of thermal field underneath an evaporative water surface, Int. J. Therm. Sci., 50, 6, 930–934, doi:10.1016/j.ijthermalsci.2011.01.001.
Carlomagno, G. M., G. Cardone (2010), Infrared thermography for convective heat transfer measurements, Exp. Fluids, 49, 6, 1187–1218, doi:10.1007/s00348-010-0912-2.
Fedorov, K. N., A. I. Ginsburg (1992), The Near-Surface Layer of the Ocean, VSP-BV, Utrecht, 256 pp.
Gulev, S. K., K. Belgaev (2012), Probability distribution characteristics for surface air-sea turbulent heat fluxes over the global ocean, J. Climate, 25, 1, 184–206, doi:10.1175/2011JCLI4211.1.
Ivanitskii, G. R., A. A. Deev, and E. P. Hizhnyak (2005), Water surface structures observed using infrared imaging, Physics-Uspekhi, 48, 11, 1151–1160, doi:10.1070/PU2005v048n11ABEH004685.
Katsaros, K. B., W. T. Liu , J. A. Businger, and J. E. Tillman (1977), Heat transport and thermal structure in the interfacial boundary layer measured in an open tank of water in turbulent free convection, J. Fluid Mech., 83, 2, 311–335, doi:10.1017/S0022112077001219.
Khundzhua, G. G., E. G. Andreev, V. N. Aksenov, A. V. Romanchenko, A. V. Nelepo, and E. N. Karavaeva (1997), Regimes of heat and mass exchange between the ocean and the atmosphere, Izvestiya, Atmospheric and Oceanic Physics, 33, 3, 269–274.
Lapshin, V. B., I. G. Ragulin (1990), On surface tension coefficient of oceanic water, (in Russian) Russian Meteorology and Hydrology, 11, 108–109.
Liu, W. T., K. B. Katsaros, and J. A. Businger (1979), Bulk parameterization of air-sea exchanges of heat and water vapor including the molecular constraints at the interface, J. Atmos. Sci., 36, 9, 1722–1735, doi:10.1175/1520-0469(1979)036<1722:BPOASE>2.0.CO;2.
Luikov, A. V. (1966), Heat and Mass Transfer in Capillary-Porous Bodies, Pergamon Press, New York, 523 pp.
McAlister, E. D., W. McLeish (1970), A radiometric system for airborne measurement of the total heat flow from the sea, Appl. Opt., 9, 12, 2697–2705, doi:10.1364/AO.9.002697.
Meier, G. (2002), Computerized background-oriented schlieren, Exp. Fluids, 33, 1, 181–187, doi:10.1007/s00348-002-0450-7.
Minnett, P. J., M. Smith, and B. Ward (2011), Measurements of the oceanic thermal skin effect, Deep-Sea Research Part II: Topical Studies in Oceanography, 58, 6, 861–868, doi:10.1016/j.dsr2.2010.10.024.
Nunez, G. A., E. M. Sparrow (1988), Models and solutions for isothermal and non-isothermal evaporation from a partially filled tube, Int. J. Heat Mass Transfer, 31, 3, 461–477, doi:10.1016/0017-9310(88)90028-2.
Scarano, F., M. L. Riethmuller (1999), Iterative multigrid approach in PIV image processing with discrete window offset, Exp. Fluids, 26, 6, 513–523, doi:10.1007/s003480050318.
Shah, M. M. (2003), Prediction of evaporation from occupied indoor swimming pools, Energy and Buildings, 35, 7, 707–713, doi:10.1016/S0378-7788(02)00211-6.
Spangenberg, W. G., W. R. Rowland (1961), Convective circulation in water induced by evaporative cooling, Phys. Fluids, 4, 6, 743–750, doi:10.1063/1.1706392.
Vinnichenko, N. A., A. V. Uvarov, and Yu. Yu. Plaksina (2012), Accuracy of Background Oriented Schlieren for different background patterns and means of refraction index reconstruction, Proc. of $15^{th}$ Int. Symp. Flow Visualization, Minsk, Belarus.
Vinnichenko, N. A., A. V. Uvarov, Yu. Yu. Plaksina, and D. A. Vetukov (2011), Study of evaporation from water reservoir, Proc. of $22^{nd}$ Int. Symp. Transport Phenom., Delft, Netherlands, 45.
Volino, R. J., G. B. Smith (1999), Use of simultaneous IR temperature measurements and DPIV to investigate thermal plumes in a thick layer cooled from above, Exp. Fluids, 27, 1, 70–78, doi:10.1007/s003480050330.
Received 28 May 2012; accepted 31 May 2012; published 4 June 2012.


Citation: Plaksina Yu. Yu., A. V. Uvarov, N. A. Vinnichenko, V. B. Lapshin (2012), Experimental investigation of near-surface small-scale structures at water--air interface: Background Oriented Schlieren and thermal imaging of water surface, Russ. J. Earth Sci., 12, ES4002, doi:10.2205/2012ES000517.
Copyright 2012 by the Geophysical Center RAS.
Generated from LaTeX source by SemTeXML, v.1.2) software package.












