RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 21, ES1002, doi:10.2205/2020ES000722, 2021
Aylin Tan1, Mahir Isik2, Hakki Senel3
1Institute of Natural Sciences, Main Science Branch of Geophysical Engineering, Sakarya University, Sakarya, Turkey
2Department of Geophysical Engineering, Sakarya University, Sakarya, Turkey
3Directorate of Mineral Research & Exploration, Ankara, Turkey
In this study, sedimentary basins were modeled by using the variable density contrast. In a sedimentary basin which might be modeled by a series of prisms juxtaposed with each other, density variation with depth was represented by quadratic function. The initial depths of the prisms were obtained by using the gravity anomaly of an infinite horizontal slab for the modeling. These depths were improved by taking into account the differences between the observed and calculated anomalies. The method was successfully examined on the theoretical models and then applied to Erzincan-Cayirli field data.
The densities of sedimentary rocks vary with some factors that are pressure, compaction, porosity, age, depth etc. For this reason, sedimentary basins can be modeled with the variable density functions [Athy, 1930; Bott, 1960; Cordell, 1973; Chai and Hinze, 1988; Rao et al., 1993]. For correct detection of the density function coefficients, density contrast-depth information is required. This density contrast-depth data can be determined by well or seismic or bore-hole data in investigation field.
Athy [1930] argued that an exponential relationship between the depth and density. It can be said that the density contrast decreases exponentially with increasing depth. Bott [1960] studied at the fundamental method, later. Based on this idea, Cordell [1973] examined the San Jacinto Graben in Southern California by using the exponential density function with the prism model. Murty and Rao [1979] interpreted the sedimentary basins using an exponential density function Rao [1986] applied a method to interpret the gravity anomaly of San Jacinto Graben, California, where sediments were filling the graben have a density contrast that can be approximated to a quadratic function. Chai and Hinze [1988] examined the Los Angeles Basin in California by using the exponential function. Litinsky [1989] interpreted a gravity anomaly of a sedimentary basin by using the concept of hyperbolic density contrast. Rao et al. [1990] evaluated the Los Angeles Basin by using the quadratic density function. Rao et al. [1993] interpreted the sedimentary basins using an exponential density function Chakravarthi et al. [2001] modeled the Tucson Basin in Southern Arizona by using the polygon model with the parabolic density function. Further Chakravarthi and Sundararajan [2005, 2006] modeled the Godawari Basin in India by using the 2.5-D vertical prism model with the parabolic density function. Silva et al. [2006] evaluated the Reconcavo Basin in Brasil by using the hyperbolic density function, too. Isik and Senel [2009] also investigated the depth of the underground basement topography of the Buyuk Menderes Basin by using the parabolic density function with 3-D inversion method. Martins et al. [2010] evaluated the performance of their method by applying it to a gravity data set from onshore and part of the shallow offshore Almada Basin on Brazil's northeastern coast [Chakravarthi, [2010] modeled the Chintalpudi sub basin in India by using strike limited listric fault structures with prescribed vertical variation in density. Chakravarthi et al. [2013] modeled The Chintalpudi subbasin by using strike limited sedimentary basins by means of growing bodies with exponential density contrast-depth variation. Silva et al. [2014] illustrated the possibility of applying the iterative correction method proposed by Bott [1960] even in sedimentary environments in which it is assumed vertical density variation. Silva et al. [2014] extend Bott method that was very efficient in estimating the basement relief of a sedimentary basin using the gravity anomaly.
In this study, sedimentary basins are modeled by using variable density contrast. For the modeling, the initial depths of prisms were determined by using the gravity anomaly of an infinite horizontal layer. These depths were corrected with the help of the differences between the observed and calculated anomalies.
The study area has a tectonic activity and carries some important structural elements. The Erzincan Basin which is one of the Neogene-Quaternary basins of the inter-mountain located during the North Anatolian Fault is approximately 50 km long and a 10 km wide. The basin is located among the North Anatolian Fault Zone (NAF), North-Eastern Anatolian Fault Zone (NEAFZ) and Ovacik Fault (OF). Akinci and Eyidogan [2000] stated that Erzincan area is very heterogenic and this heterogeneity is related with the presence of the different directions of faults, a medium that has a strong lamination, magmatic intrusions and the source of heat flow.
The density-depth relationship in the sedimentary basins can be approximated by a quadratic function [Hudson and Lipka, 1940; Rao, 1986]:
\begin{equation} \tag*{(1)} \Delta \rho (h) = a + bh + ch^{2} \end{equation}In the equation (1), $\Delta \rho (h)$ is density contrast at depth $h$; $a$, $b$ and $c$ are coefficients that represent the state when the depth increases, the density contrast decreases. These coefficients can be determined by being applied to the density contrast-depth data with the least squares approach. The density contrast data depending on the depth can be obtained by using well or seismic studies or bore-hole data in the study area [Isik and Senel, 2009].
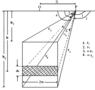
 |
| Figure 1 |
In Figure 1 the symbols are shown as $w$ is the prism half-width, $h_1$ is the upper depth of prism, $h_2$ is the lower depth of prism:
\begin{eqnarray*} r_{1} =\left[h_{1}^{2} +(x+w)^{2} \right]^{1/2}, \, \beta_{1} = \frac{\pi}{2} +\arctan \left[\frac{x+w}{h_{1}} \right] \end{eqnarray*} \begin{eqnarray*} r_{2} =\left[h_{1}^{2} + (x-w)^{2} \right]^{1/2}, \, \beta_{2} = \frac{\pi}{2} +\arctan \left[\frac{x-w}{h_{1}} \right] \end{eqnarray*} \begin{eqnarray*} r_{3} = \left[h_{2}^{2} + (x-w)^{2} \right]^{1/2}, \, \beta_{3} = \frac{\pi}{2} +\arctan \left[\frac{x-w}{h_{2}} \right] \end{eqnarray*} \begin{eqnarray*} r_{4} = \left[h_{2}^{2} + (x+w)^{2} \right]^{1/2}, \, \beta_{4} = \frac{\pi}{2} +\arctan \left[\frac{x+w}{h_{2}} \right] \end{eqnarray*}When calculating the gravity anomaly of each of prisms, the following points should be kept in mind
(i) $x$ is non-zero ($x \neq 0$) for all positive values of; $\beta_1 = \beta_2 = \pi$;
(ii) $x$ is non-zero ($x \neq 0$) for all negative values of; $\beta_1 = \beta_2 = 0$;
(iii) For $x = 0$; $\beta_1 = \pi$ and $\beta_2 = 0$.
The surface gravity effect of the prism which has quadratic density contrast can be written as
\begin{eqnarray*} g(x) = A \left[ h_{2} \beta_{43} + (x + w)L_{4} - (x - w)L_{3} \right]+ \end{eqnarray*} \begin{eqnarray*} B \left[ h_{2}^{2} \beta_{43} + (x-w)^{2} \beta_{23} - (x + w)^{2} \beta_{14} + 2 w h_{2} \right] + \end{eqnarray*} \begin{eqnarray*} C \left[ h_{2}^{3} \beta_{43} + (x-w)^{3} L_{3} - (x + w)^{3} L_{4} +w h_{2}^{2} \right] \end{eqnarray*} \begin{eqnarray*} A = 2 k_0 a, \quad \beta_{14} = \beta_1 - \beta_4 \end{eqnarray*} \begin{eqnarray*} B = k_0 b, \quad \beta_{23} = \beta_2 - \beta_3 \end{eqnarray*} \begin{eqnarray*} C = 2 k_0 \frac{c}{3}, \quad \beta_{43} = \beta_4 - \beta_3 \end{eqnarray*} \begin{eqnarray*} L_{3} =\log_{e} \left[\frac{r_{3}}{x-w} \right], \quad L_{4} =\log_{e} \left[\frac{r_{4}}{x+w} \right] \end{eqnarray*}here, $k_0$ is "The Universal Gravitation Constant" [Rao, 1986].
Sedimentary basins where changes in the density contrast versus depths can be modeled from gravity anomalies by using the quadratic density function. If density contrast values of sedimentary rocks according to the basement at specific depths are known, $a$, $b$ and $c$ coefficients can be determined by using (1).
Basin is designed as a set of adjacent two-dimensional vertical prisms. Widths of the prisms are equal to observation range. For a basin that is on the surface, top of the depths of all prisms are considered as on the surface of the Earth. Thus, the problem of modeling turns into (or is reduced to) the problem of $m$-number identification of the depth of the prism bottoms. Here, $m$ is the number of observations.
Differences between $g_{\mathrm{obs}} (i)$ observed anomalies and $g_{\mathrm{cal}} (i)$ calculated anomalies can be written as
\begin{eqnarray*} e_i = g_{\mathrm{obs}} (i) - g_{\mathrm{cal}} (i), \quad i = 1, 2, \ldots , m \end{eqnarray*}These differences are used for regulation of the prism depths [Bott, 1960],
\begin{eqnarray*} h_{i}^{(j+1)} = h_{i}^{(j)} + \frac{e_{i}}{2\pi k_{0} a}, \quad j=0,1,\ldots, n \end{eqnarray*}here, $n$ is the iteration number.
We used a stopping criterion that interrupts the process if the residue between observed and predicted data was smaller than a preset value, usually a percentage of the expected noise level in the data. The stopping criterion is 0.00025 m that m is the observation number. That procedure was originally used by Bott in 1960.
 |
| Figure 2 |
 |
| Figure 3 |
On the basin modeling that has been chosen as the theoretical model during a profile that 55 km long, with 2.5 km intervals, 23 numbers observation points have been determined. Density contrast-depth values have been taken as $\Delta \rho$ (1 km)$ = - 0.60$ gr/cm$^3$, $\Delta \rho$ (3 km)$ = - 0.40$ gr/cm$^3$, and $\Delta \rho$ (4 km)$ \, = - 0.35$ gr/cm$^3$ By using these values, coefficients of the quadratic density function are obtained as $a= -0.750$, $b= 0.167$ and $c= -0.017$, respectively. Thus the quadratic density function is obtained as $\Delta \rho (h) = - 0.750 + 0.167 h - 0.017 h^2$ for the model. The graphic of density contrast versus depth for the theoretical model at Figure 2 and theoretical basin modeling at Figure 3 are shown.
The field data may contain some observation or truncation error that need to take into account. For this reason, the noise that is between $-1$ and $+1$ mGal has been added to the model data by production random numbers. Thus, the method has been investigated to what extent is effective on the noise-data. Further noise-theoretical model have been examined. The modeling results that belong to the noise-model are seen at Figure 3.
We presented the estimated depths over a basement relief of a sedimentary basin in one profile from the gravity anomaly with a quick and efficient procedure that did not require inversion procedures. In that procedure: i) The estimated depths were corrected iteratively by Bott method [Bott, 1960]; ii) A presumed information was incorporated, within the sedimentary packet the density increased with depth in accordance with a square law. That depth estimation procedure was applied to a synthetic data set showing the validity of it, it was also applied to the data set Erzincan-Cayirli Basin. This paper illustrates the possibility of applying the iterative correction method proposed by Bott [1960] even in sedimentary environments in which it is assumed vertical density variation.
 |
| Figure 4 |
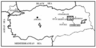
Cayirli District, where is the study area, is a member of Erzincan City and is at distance of 44 km. The city is at Eastern Anatolia and Gumushane City is located at North-side of it, Tunceli City is located at South-side of it, Sivas City is located at West-side of it and Erzurum City is located at east-side of it (Figure 4).
 |
| Figure 5 |
Study area has a very serious importance as tectonically. There are important faults and basins. As geological structure, at Erzincan Plain, where obtained on second, third and fourth ages from old ones to young ones, there are Paleozoic age and unweather metamorphic sequence, Mesozoic chalks, Cretaceous flysch, Eocene flysch, Neogene chalks, Neogene terrestrial and volcanic rocks, Quaternary age travertine, terrace, alluvium and alluvial conies, respectively. Further on the study areas, probability of occurrence of serpentine under the under the sedimentary rocks is high. Further not only the Mountain Kesis that are at the south part but also the Mountains Kop that are outside of the study area are covered by the serpentine and it can be thought that the serpentine was connected under the ground [Demirmen, 1965]. The Erzincan Plain collapsed because of tectonic movements that had epeirogenic character at the upper parts of the Neogene ages (Figure 5).
 |
| Figure 6 |
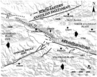
The Erzincan Plain, where is one of the Neogene-Quaternary connecting-mountain plains, is located on during the North Anatolian Fault, has about 50 km length and 10 km width. The plain is located on among the North Anatolian Fault Zone (NAFZ), North-East Anatolian Fault Zone (NEAFZ) and Ovacik Fault (OF). NEAFZ that is on the northern side, is a dextral fault zone that limited the Black Sea Mountain Series at the southern part. Tracks of the dextral faulting NAFZ are seen at a wider zone that is northern and southern part of the Erzincan Plain and the fault has a collusion component at this region, too. As seen on the Figure 6, first segment of the probable faults (F1) is located on between the Yedisu Plain and the Erzincan Plain about of $115\mbox{°}$ azimuth and the half-western part of this segment extends during the Euphrates Valley. Second segment (F2) limits on the North edge of the plain and has an angle about of $125\mbox{°}$ azimuth. The morphological features of the half eastern part of this segment are covered by some young sediments and volcanic rocks at several regions at the area. There is a pull-apart step of about 5 km between F1 and F2. At the northwest of the basin other segment (F3) extends towards to west by an angle of $20\mbox{°}$ with the previous segment to perform the bending inward (at $105\mbox{°}$ azimuth). NE–SW trending dextral O.F. intersects with NAF at the southern-east of the Erzincan basin (F1 and F2). Today the Erzincan Basin is pulled apart by extending step that is at between F1 and F2 and movement of the OF [Kaypak and Eyidogan, 2002].
Another fault, which effects Erzincan and its surrounding, is NAEFZ that has NE–SW strike-slip faulting. This fault lies down as a wide zone towards to the North-West and its faulting character is the left lateral strike-slip suture zone. The geological slip velocities, that were obtained on these faults, were found as approximately 1 cm/year for NAF, approximately 0.15–0.2 cm/year for OF and NEAF [Kaypak and Eyidogan, 2002]. Kaypak and Eyidogan [2005] stated that the pull-apart mechanism was induced at the westwern western of the Erzincan Basin. Ketin [1976], Eyidogan [1992], Fuenzalida et al. [1997], Akinci and Eyidogan [2000] determined that the Erzincan Pull-Apart Basin is characterized by young sediments. Akinci and Eyidogan [2000] have revealed that Erzincan region is very heterogenic. They specified that this heterogeneity is related with existence of faults that had different strike, a medium that has a hard bedding, magmatic intrusions and source of heat flows.
Aktimur et al. [1995] determined that the mountains continue to ascend in the study area, depending on the development of the Erzincan basin, due to the maturity stage of conditioning has not passed yet. Further they emphasized that in parallel with the formation of the Erzincan basin, very large elevations in the area consists at the Upper Miocene-Present stage, these elevations slightly continued at Present Stage, too. Ardos [1996] emphasized that epeirogenical elevation has been continuing from beginning of the late Miocene to present, consists of parallel faults around of the Erzincan Plain today and subsequent increase in the thickness of the alluvial plain, which is full of silt stressed.
Elevated edges of the basin by some faults and so collapsing of the basin, very wide sedimentary fans grow up in the area [Kaypak and Eyidogan, 2002]. During the NAF the seismic activity was always high (Figure 6). On the fault that practically continuously causes some ruptures, there have occurred some earthquakes which happened between 1939 and 1967 years and migrated from the east to the west [Kuscu et al., 1992].
When the Erzincan Earthquake (1939, $Mw=7.9$) occurred, the horizontal displacement was 3.7 m. at the Valley Kelkit. That important displacement which occurred during a bit little seconds, in the course of time effected on the river net and topography of the regions, too [Ardos, 1996]. Eyidogan [1992] emphasized that the main shock of the Erzincan Earthquake (1992, $Mw=6.9$) occurred at the Erzincan Basin which was a pull-apart basin quality that was wide, complex and thick sediment; and this earthquake was happened by a complex faulting that occurred by a complex faulting that occurred at the south-east of the basin and other some segments of the NAF have started to activity in the region, too (Figure 6).
For accurately determination of the quadratic density function coefficients, we need to have been taken some information of the density contrast-depth on the basin. This density contrast-depth can be obtained from well-logging or seismic examinations or drilling data that have been taken on investigated area. In this study at proving of investigated density contrast-depth data, we used the Neftlik-4 (N4) drilling works that General Directorate of Mineral Research & Exploration (M.T.A.) has drilled and the stratigraphy of the field.
By considered all geological and drilling information, this state can be thought at the first level it is conglomerate 2.1–2.7 gr/cm$^3$, at the second level it is sandstone 2.59–2.72 gr/cm$^3$, at the third level it is marl 2.0–2.6 gr/cm$^3$ and forth level it is serpentine 2.8–3.1 gr/cm$^3$ [Erden, 1979; Sazhina and Grushinsky, 1971; Telford et al., 1982].
 |
| Figure 7 |
Although researchers studied up to 2049 m. at the drilling investigation (Figure 7), they could not have reached to the basement. But Demirmen [1965] emphasized that the probability of locating of the serpentine under the sedimentary rocks was powerful at the study area. Further he determined that not only the Mountain Kesis that was at the south part but also the Mountains Kop that were outside of the study area covered by the serpentine and they were connected from the underground at the area. So we decided that the basement of the basin was the serpentine.
 |
| Figure 8 |
As seen at the Figure 8, the cross-section of the Profile A-A$'$, that had 17 km length, was taken from the residual gravity anomaly map which belonged to the Erzincan-Cayirli Region, was sampled with 1 km intervals and then the observation points that were numbers of 18 were obtained.
 |
| Figure 9 |
From this data, for the basin model that belonged to the profile A-A$'$, the density contrast-depth data were determined as $\Delta \rho $ (0.30 km)$ = -0.33$ gr/cm$^3$, $\Delta \rho $ (0.55 km)$ = -0.30$ gr/cm$^3$, and $\Delta \rho $ (1.80 km)$ = -0.20$ gr/cm$^3$ (Figure 9). By using these data, the quadratic density function coefficients were found as $a= -0.370$, $b= 0.143$ and $c= -0.027$. Thus after determination of the quadratic function coefficients, we might start to interpret the model.
 |
| Figure 10 |
For the Profile A-A$'$, the density function was found as $\Delta \rho (h) = -0.370 + 0.143 h - 0.027 h^2$. We determined the maximum depth of the basin as 2.2608 km by examination the Profile A-A$'$ by using the quadratic density function (Figure 10).
While the basins are being interpreted, a trapezoidal model or the prismatic bodies can be used. When the floor of the basin somewhat has an undulating structure, we have thought that the trapezoidal model may not give us a very good result. For that reason in this study we accepted that the basin had occurred from side by side adjacent prismatic bodies.
Especially while an inversion was studied at the self-sourced geophysical (The gravity, the magnetics etc.), the selection of the initial parameters is very important. The initial model has to be chosen to represent the true geological structure well. If we select a false initial model, the inversion may cause the unsolved results or may create the masses that are outside of the normal limits. In order to avoid from these unsuccessful states, the initial depth of each prism was found by using the gravity anomaly of an infinite horizontal layer.
The method was very successful for the theoretical models. Especially the depths, that were calculated at the wings of the basin namely parts which were near to the surface, fitted into one another true depths full-accuracy. Further although chosen noise interval was very large, successful results were obtained at the noise-model, too.
After the theoretical model studies that were obtained successful results, the method was applied on the Erzincan-Cayirli field data. For determination truly of the density function coefficients that has a very important role at the method, the density contrast-depth information, that can be obtained from the well-logging, the seismic or drilling works at the study area, is needed. In this study, such information that belonged to the Erzincan-Cayirli Region, were tried to determine by using the drilling data and the geology of the area. But although we did not coincide with the drilling, Demirmen [1965] took attention that the basement was serpentine. Therefore we obtained the quadratic density function, which represented the basin, by using thicknesses of determined layers and the density contrast between the basement and these layers.
In this study the maximum depth of the sedimentary basin was determined as 2.2608 km. On the basins that were in the region, several researchers examined. Kaypak [2002] emphasized that the sedimentary thickness of the Erzincan Basin was 3000 m. Kaypak and Eyidogan [2005] determined that the maximum depth of the Erzincan Basin had changed from 500 m to 3500 m. Akinci and Eyidogan [2000] emphasized that the thickness of the basin was up to 3 km. Kaypak and Eyidogan [2002] defended that there were a sudden increment at the velocity values on the layer that was at the depth of 2 km and that layer was versus to more strength as lithological. Canbay [1999] mentioned that the average depth changed between 1 km and 2.5 km values in the region. Aktar et al. [2004] determined that the thickness of the unconsolidated lower soft sediments approached to 3 km. Not only these depths that were shown as samples, but also not being obtained to the basement rock up to the depth of 2.049 km, supply that the basin depth that was determined as 2.2608 km. The increment of this depth that was the basin center can be thought that there would have been a sudden collusion or a buried fault (Figure 10).
Further the epicenter of the Erzincan Earthquake (1939, $Mw=7.9$) was close to the study area. So we can say that the basin was affected by the NAFZ, NEAFZ and OF (Figure 6). Erzincan and vicinity of Erzincan have been frequently effected by large magnitude earthquakes because of geological and tectonics activities in the area. According to obtained data for the historical terms (Year 1900 ago), a lot of destructive earthquakes occurred in Erzincan and vicinity of the region. But when the geological and tectonics structures of the study area are considered, this is certain that those earthquakes are related with NAFZ, NEAFZ and OF [Eyidogan, 1994].
Akinci, A., H. Eyidogan (2000) , Scattering and anelastic attenuation of seismic energy in the vicinity of North Anatolian Fault Zone, eastern Turkey, Physics of the Earth and Planetary Interiors , 122, p. 229–239, https://doi.org/10.1016/S0031-9201(00)00196-5.
Aktar, M., C. Dorbath, E. Arpat (2004) , The Seismic velocity and fault structure of the Erzincan basin, Turkey, using local earthquake tomography, Geophysical Journal International Seismology, 156, p. 497–505, https://doi.org/10.1111/j.1365-246X.2004.02081.x.
Aktimur, H. T., T. Yildirim, M. Sariaslan, et al. (1995) , The Geology of Erzincan city's around General Directorate of Mineral Research & Exploration (M.T.A.), Report, Ankara, no. Report Number 9792, p. 43–57.
Ardos, M. (1996) , Quaternary geomorphology of Turkey, Cover 1, p. 116–119, Cantay Bookshop, Istanbul.
Athy, L. F. (1930) , Density, porosity and compaction of sedimentary rocks, Bulletin of the American Association of Petroleum Geologists, 14, p. 1–24, https://doi.org/10.1306/3D93289E-16B1-11D7-8645000102C1865D.
Bott, M. H. P. (1960) , The use of Rapid Digital Computing Methods for Direct Gravity Interpretation of Sedimentary Basins, Geophys. J. Int., 3, no. 1, p. 63–67, https://doi.org/10.1111/j.1365-246X.1960.tb00065.x.
Canbay, M. M. (1999) , Determination of the subsurface structure in the Erzincan region by using inversion and forward solutions University of Kocaeli, Journal of Applied Geosciences, 3, p. 69–80.
Chai, Y., W. J. Hinze (1988) , Gravity inversion of an interface above which the density contrast varies exponentially with depth, Geophysics, 53, no. 6, p. 837–845, https://doi.org/10.1190/1.1442518.
Chakravarthi, V., S. B. Singh, B. G. Ashok (2001) , INVER2DBASE – A program to compute basement depths of density interfaces above which the density contrast varies with depth, Computers and Geosciences, 27, p. 1127–1133, https://doi.org/10.1016/S0098-3004(01)00035-8.
Chakravarthi, V., N. Sundararajan (2005) , Gravity modeling of 2.5-D sedimentary basins-a case of variable density contrast, Computers and Geosciences, 31, p. 820–827, https://doi.org/10.1016/j.cageo.2005.01.018.
Chakravarthi, V., N. Sundararajan (2006) , Gravity anomalies of 2.5-D multiple prismatic structures with variable density: A Marquardt Inversion, Pure and Applied Geophysics, 163, p. 229–242, https://doi.org/10.1007/s00024-005-0008-8.
Chakravarthi, V. (2010) , LSTRKFALTG – A forward modeling program to compute theoretical gravity anomalies of strike limited listric fault structures with prescribed vertical variation in density, Computers & Geosciences, 36, p. 675–679, https://doi.org/10.1016/j.cageo.2009.09.007.
Chakravarthi, V., S. R. Sastry, B. Ramamma (2013) , MODTOHAFSD – A GUI based JAVA code for gravity analysis of strike limited sedimentary basins by means of growing bodies with exponential density contrast-depth variation: A space domain approach, Computers & Geosciences, 56, p. 131–141, https://doi.org/10.1016/j.cageo.2013.02.005.
Cordell, L. (1973) , Gravity analysis using an exponential density-depth function, San Jacinto Graben, California, Geophysics, 38, p. 684–690, https://doi.org/10.1190/1.1440367.
Demirmen, F. (1965) , Geology and petroleum facilities of Cayirli district (Erzincan) area. (The readers: I43b1, I43b2, I43b4), General Directorate of Mineral Research & Exploration (M.T.A.) Report, Ankara, Turkey, no. Report Number: 4062, p. 1–70.
Erden, F. (1979) , Applied gravity, General Directorate of Mineral Research & Exploration (M.T.A.) Publications, Ankara, Turkey, no. Number of the Training series: 21, p. 47–48.
Eyidogan, H. (1992) , A discussion on the characteristics of the main shock and aftershocks of the 13, March, 1992 Erzincan Earthquake, Geophysics, 6, p. 103–112.
Eyidogan, H. (1994) , Examination of the geophysical properties of the 13.03.1992 Erzincan Earthquake's parameters of the main shock and the aftershock and earthquake area. The Project No: 362, Technical University Research Found, Istanbul.
Fuenzalida, H., L. Dorbath, et al. (1997) , Source mechanism of the 1992 Erzincan earthquake, from detailed aftershock analysis and broad band body wave inversion: tectonics of the Erzincan basin and evidences of fault decoupling on the North anatolian fault, Geophysics Int. J., 129, p. 1–28, https://doi.org/10.1111/j.1365-246X.1997.tb00935.x.
Hudson, R. G., J. Lipka (1940) , A Manual of Mathematics, 1–10 pp., Cambridge Univ. Press, Mass.
Isik, M., H. Senel (2009) , 3D gravity modeling of Buyuk Menderes basin in Western Anatolia using parabolic density function, Journal of Asian Earth Sciences, 34, p. 317–325, https://doi.org/10.1016/j.jseaes.2008.05.013.
Kaypak, B. (2002) , Determination of 3-D velocity structure of the Erzincan Basin by local earthquake tomography, PhD. Thesis, Technical University Nature and Science Institute, Istanbul.
Kaypak, B., H. Eyidogan (2002) , Determination of Erzincan basin and surrounding and the upper-crust velocity structure (1D), Journal of Engineering Istanbul Technical University (ITU), 1, no. 2, p. 107–122.
Kaypak, B., H. Eyidogan (2005) , One-dimensional crustal structure of the Erzincan basin, Eastern Turkey and relocations of the 1992 Erzincan earthquake ($Ms=6.8$) aftershocksequence, Physics of the Earth and Planetary Interiors, 151, p. 1–20, https://doi.org/10.1016/j.pepi.2004.11.009.
Ketin, I. (1976) , A comparison between the San Andreas and the North Anatolian faults, Bulletin of the Geological Society of Turkey, 19, p. 149–154.
Kuscu, I., A. A. Barka, et al. (1992) , The Radon Gas (Alpha Velocity) Measurements at some faults of the North Anatolian Fault zone, Journal of Geological Engineering, 40, p. 33–40.
Litinsky, V. A. (1989) , Concept of effective density: Key to gravity depth determinations for sedimentary basins, Geophysics, 54, p. 1474–1482, https://doi.org/10.1190/1.1442611.
Martins, C., V. Barbosa, J. Silva (2010) , Simultaneous 3D depth-to-basement and density-contrast estimates using gravity data and depth control at few points, Geophysics, 75, no. 3, p. I21–I28.
Murty, I. V. R., D. B. Rao (1979) , Gravity anomalies of two-dimensional bodies of irregular cross-section with density contrast varying with depth, Geophysics, 44, p. 1525–1530, https://doi.org/10.1190/1.1441023.
Rao, D. B. (1986) , Modelling of sedimentary basins from gravity anomalies with variable density contrast, Geophysical Journal International, 84, no. 1, p. 207–212, https://doi.org/10.1111/j.1365-246X.1986.tb04353.x.
Rao, D. B., M. J. Prakash, N. R. Babu (1990) , 3D and 2D modelling of gravity anomalies with variable density contrast, Geophysical Prospecting, 38, p. 411–422, https://doi.org/10.1111/j.1365-2478.1990.tb01854.x.
Rao, D. B., M. J. Prakash, N. R. Babu (1993) , Gravity interpretation using Fourier transforms and simple geometrical models with exponential density contrast, Geophysics, 58, p. 1074–1083, https://doi.org/10.1190/1.1443491.
Sazhina, N., Y. N. Grushinsky (1971) , Gravity Prospecting, 411–414 pp., Mir Publishers, Moscow.
Silva, J., D. Costa, V. Barbosa (2006) , Gravity inversion of basement relief and estimation of density contrast variation with depth, Geophysics, 71, no. 5, p. J51–J58.
Silva, J., D. Santos, K. Gomes (2014) , Fast gravity inversion of basement relief, Geophysics, 79, no. 5, p. G79–G91, https://doi.org/10.1190/geo2014-0024.1.
Telford, W. M., L. P. Geldart, et al. (1982) , Applied Geophysics, 25 pp., Univ. Press, Cambridge.
Received 28 January 2020; accepted 8 June 2020; published 19 January 2021.


Citation: Tan Aylin, Mahir Isik, Hakki Senel (2021), Gravity interpretation of the Erzincan-Cayirli Basin its connection with the North Anatolian Fault Zone using quadratic density function, Russ. J. Earth Sci., 21, ES1002, doi:10.2205/2020ES000722.
Copyright 2021 by the Geophysical Center RAS.