RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 20, ES4007, doi:10.2205/2020ES000735, 2020

Kinematics of interacting solitons in two-dimensional space

L. A. Ostrovsky^1,2, Y. A. Stepanyants^3,4

¹University of Colorado Boulder, Boulder, Colorado, USA

²Institute of Applied Physics RAS, Nizhny Novgorod, Russia

³School of Sciences, University of Southern Queensland, Toowoomba, Australia

⁴Nizhny Novgorod State Technical University n.a. R. E. Alekseev, Nizhny Novgorod, Russia

Abstract

A simple kinematic approach to the description of interaction between solitons is developed. It is applicable to both integrable and non-integrable two-dimensional models, including those commonly used for studying surface and internal oceanic waves. This approach allows obtaining some important characteristics of the interaction between solitary waves propagating at an angle to each other. The developed theory is validated by comparison with the exact solutions of the Kadomtsev-Petviashvili equation and then applied to the observed interaction of solitary internal waves in a two-layer fluid within the two-dimensional Benjamin-Ono model.

1. Introduction

Figure 1

As it is well-known, solitary waves are a rather ubiquitous phenomenon in the oceans [Apel et al., 2007]. One of the interesting specific features of these phenomena is the oblique interaction between the solitons that were observed for the surface waves in laboratory conditions back in 1960s (see, e.g., [Wiegel, 1964] and references therein). The in situ observations were made in particular by Ablowitz and Baldwin [2012]. Three examples of solitary wave interactions observed on a surface of shallow water are shown in Figure 1.

Figure 2

Similar structures were observed for internal waves. The first was, apparently, the laboratory experiment by Maxworthy [1980]. In the ocean, the interacting internal soliton fronts were observed by many researchers, in particular, by Small [2002] and Wang and Pawlowicz [2012]. Figure 2 shows an example from the latter work; the data from this paper will be used below for the estimation of the wave pattern motion using our theoretical findings.

Regarding the theory of the phenomenon, one can refer to the works by Miles [1977a, 1977b] who considered the oblique interaction of two solitary waves of the KdV-Boussinesq type using an approximate method similar to that suggested by Whitham [1967] for the one-dimensional soliton interaction. He suggested a classification of interactions as weak and strong depending on the relationship between the parameter of nonlinearity $N$ and the angle $\gamma$ between the soliton fronts, where $N$ is proportional to the soliton amplitude. According to this classification, the interaction is weak if $N \ll \sin^{2} (\gamma/2$) and strong otherwise. Miles also considered the "resonant" interaction of solitons when the wave pattern consists of three solitary waves stationarily moving in a certain direction.

Here we develop a kinematic approach to the stationary moving a two-soliton pattern in a general case and demonstrate the validity of this approach by comparison with the exact two-soliton solutions, resonant and non-resonant. From the available two-dimensional model equations describing, in particular, surface and internal solitary waves (such as 2D versions of the Boussinesq, Gardner, and Benjamin-Ono equations), only the Kadomtsev-Petviashvili (KP) equation is completely integrable [see, e.g., Ablowitz and Segur, 1981; Anker and Freeman, 1978; Newell and Redekopp, 1977; Satsuma, 1976; Zakharov, 1980]. This allows one to construct exact two-soliton solutions describing the interaction of two solitary waves moving at an angle to each other. Here we use the corresponding exact solutions of the KP equation for two-soliton structures moving as a whole. Besides verifying the simple kinematic approach, we use the latter to define the direction and speed of motion of the whole wave pattern that was not disclosed in exact solutions thus far. Within the suggested approach, one only needs to know the speeds of solitary waves and directions of their propagations in the chosen coordinate frame. These parameters are usually measurable or observable in experiments (see, for example, Figure 1 and Figure 2) and known a priori within many realistic model equations (even non-integrable). Note that even if the total interaction pattern moves stationary, each soliton propagates in the direction perpendicular to its front, so that the total pattern includes "sliding" of soliton fronts with respect to each other.

2. Kinematics of Plane Soliton Fronts

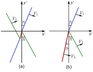Figure 3

Some important properties of the oblique interaction of solitons can be understood using a simplified physical consideration of interacting solitons regardless of a specific model. In this Section we choose the coordinates in which the total pattern of the interacting solitons moves without distortion along the $x'$-axis with the constant speed $U$, so that it is immovable in the coordinates $ \xi = x' - Ut$ and $y'$. Figure 3 schematically shows this configuration for two cases. In Figure 3a one can see the general case when two soliton fronts experience finite shifts in space due to the nonlinear interaction (more details will be given in the next Section using exact solution of the KP equation); the shifts are characterized by a bridge between the left and right pairs of soliton fronts. In Figure 3b the special, resonant case is shown when the phase shifts become infinite and the bridge transforms into the third soliton.

The equation that secures the stationary motion along the $x'$ axis, i.e., the same velocity $\widetilde{U}$ of the entire wave pattern is:

where $V_{1,2}$ are the moduli of solitary wave velocities which are normal to their fronts in isotropic media and defined by a solution for a single soliton in the absence of the second one (which is evident for the front parts far from the interaction area); we assume that they are known. The angles $\gamma_{1,2}$ are measured from the $y'$-axis normal to the direction of motion of the whole pattern (see Figure 3). It should be emphasized that this simple approach is valid in an arbitrary inertial reference frame provided that the velocities of solitary waves are taken in that reference frame. This reasoning is quite general and applicable to any model possessing solitary wave solutions and having a solution in the form of a steadily moving set of solitons. As mentioned, the individual solitons propagate perpendicular to their fronts, and the unchanged total pattern is preserved by synchronization of their propagation (the same is true for the linear wave fronts reflecting from a rigid boundary).

In the exact solutions of the KP equation described below in a different coordinate frame $x,y$, the direction of the pattern motion and its speed $U$ are not determined explicitly. However, the amplitudes of solitons, their velocities $V_{1,2}$, and the angle between their fronts, $\gamma = \gamma_{1} + \gamma_{2}$, are independent of the orientation of a coordinate system. To relate these values with $U$ and the direction of pattern motion along the $x'$-axis, we rewrite Eq. (1) in a slightly different form, for example, for the angle $\gamma_1$ as:

For small angles $\gamma_{1,2}$ (as in the KP equation considered below) and small nonlinearity when $\widetilde{V}_{1,2} = c (1 + s_{1,2} )$, where $c$ is the speed of long linear waves and $s_{1,2}\ll 1$ this relationship reduces to $ \gamma_1 \approx (2 |\Delta s| + \gamma^{2})/2 \gamma$ or $ |\Delta s| \approx \gamma_{1} |\Delta \gamma|$, where $\Delta s = s_{2}- s_{1}$ and $\Delta \gamma = \gamma_{2}- \gamma_{1}$. Because we assumed that $\widetilde{V}_{1,2}$ and $\gamma$ are known, the expression (2) determines the direction of the pattern motion, and its speed $\widetilde{U}$ is now given by Eq. (1). We shall illustrate below the details by a few examples.

In the context of the KP equation in application to a real physical system when the nonlinearity is assumed to be small, the total velocities of solitons $\widetilde{V}_{1,2} $ are close to each other and all angles in Eq. (2) are small. The important role in the soliton interactions is played by the front shifts which are characterized by a bridge between two pairs of incoming and outcoming fronts shown in Figure 3a. As mentioned, at some relationship between the solitary wave parameters, the bridge becomes infinitely long and reduces to the third solitary wave; in this case, the wave pattern represents a resonant triad shown in Figure 3b. For the triad pattern (or if a bridge of a finite length is sufficiently long to be close to a soliton), the kinematic relation (1) should be met for any pair of solitons:

The relations (2) and (3) allow us to determine both the direction and speed of the pattern motion in any reference frame.

3. Exact Analytical Solution for Two-Soliton Interaction in the KP2 Model

The simplified approach developed above can be demonstrated in application to the Kadomtsev-Petviashvili equation with the "normal dispersion" dubbed the KP2 equation. The equation was derived for weakly nonlinear wave beams when the wave fronts can slightly deviate from the direction of propagation coinciding with the $x$-axis [Kadomtsev and Petviashvili, 1970]. Here we briefly discuss some analytical solutions of the KP2 equation [Ablowitz and Segur, 1981; Anker and Freeman, 1978; Newell and Redekopp, 1977; Satsuma, 1976; Zakharov, 1980] and compare them with the results presented in Section 2.

Consider the KP2 equation in the coordinate frame moving along the $x$-axis with the speed of long linear waves $c$:

This equation is completely integrable by the inverse scattering method; its solitary solutions can be presented in the most convenient form through the Hirota transform (see e.g., [Ablowitz and Baldwin, 2012; Ablowitz and Segur, 1981; Anker and Freeman, 1978; Newell and Redekopp, 1977; Satsuma, 1976]). With the help of the ansatz

Eq. (4) can be presented in the bilinear form:

The one-soliton solution to this equation is:

where $k$ and $l$ are arbitrary parameters and

In the original variables this solution represents a soliton:

The soliton amplitude is determined solely by the parameter $k$: $A_s = 3 \beta k^{2}/\alpha$, whereas its speed depends both of $k$ and $l$:

where $\varphi = \tan^{ -1}(l/k)$ is the angle between the direction of soliton propagation normal to its front and the $x$-axis. Note that in the Korteweg-de Vries (KdV) equation which is the particular case of the KP2 equation when $\varphi = 0$, the relationship between the soliton speed and amplitude is $V_{s} = \alpha A_s/3$.

The soliton propagates at an angle to the horizontal axis $x$ and the components of the soliton velocity $V_{s} = (V_{x}, V_{y}$) are:

The two-soliton solution has the form:

where $\omega _{i} \left(k_{i} ,l_{i} \right) = \beta k_{i}^{3} + \frac{c}{2} \frac{l_{i}^{2}}{k_{i}}$ $(i = 1, 2)$, $F = \ln B$,

and $\tan \varphi_{1,2} = l_{1,2}/k_{1,2}$, $\varphi_{1,2}$ are the angles between the directions of soliton propagation and $x$-axis.

In general, (12) describes the interaction of two plane solitons, experiencing the front shifts in space after the interaction; the typical configuration is similar to what is shown in Figure 1a or in Figure 3a.

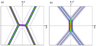Figure 4

The two-soliton solution (12) is non-singular if $B \geq 0$, and the spatial shift of each soliton front due to interaction (see Figure 3 and Figure 4) is determined by the parameter $\Phi$. Two examples of a two-soliton solution as per Eqs. (12) and (5) are shown in Figure 4 for $\eta (x, y, 0)$. At $t \ne 0$ the total pattern moves as a whole in some direction $x'$ to be determined.

The length of the bridge between the soliton fronts depends on the parameter $B$ which determines the phase shift $\Phi$ in the solution (12). When the soliton parameters $k_{1}, k_{2}, l_{1}$, and $l_{2}$ are such that $B$ is close to one (for example, if $k_{1} \gg k_{2}$ or vice versa), the front shifts are very small. However, as one can see from Eq. (13) $B$ cannot be equal to one exactly, and therefore, within the KP2 model, the front shift never equals to zero.

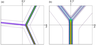Figure 5

When the soliton parameters are such that $B \rightarrow 0$, the front shift goes to minus infinity, and the bridge between the soliton fronts becomes infinitely long (see Figure 5a. In the limiting case, the bridge represents a new soliton with the amplitude $A_{3} = 3\beta (k_{1}-k_{2})^{2}/\alpha$ which is less than $A_{1}$ and $A_{2}$, and the total solution represents a triad of resonantly interacting solitons (see [Ablowitz and Baldwin, 2012; Ablowitz and Segur, 1981; Anker and Freeman, 1978; Miles, 1977b; Newell and Redekopp, 1977; Satsuma, 1976]). In another limiting case when $B \rightarrow \infty $ and correspondingly $\Phi = \ln B \rightarrow \infty$, the two-soliton solution degenerates again into the triad but of a different configuration (see Figure 5b. The amplitude of the third, resonant soliton is higher than the amplitudes of two other solitons $A_{3} = 3 \beta (k_{1} + k_{2})^{2}/\alpha$.

4. Comparison of the Kinematic Approach and Exact Solutions

As has been mentioned in Section 2, the soliton parameters were taken in the reference frame moving along the $x'$-axis with an arbitrary speed, whereas in the KP2 equation (4), the coordinate $x$ is actually $ \xi = x - ct$, and the equation {per se} is valid if soliton speeds are small, $V_{1,2} \ll c$. Here in contrast to Section 2, $V_{1,2}$ is the nonlinear correction to the wave speed and it is presumed that in the physical coordinate frame the total speed of each soliton is $\widetilde{V}_{1,2} = c (1 + s_{1,2})$, where $s_{1,2} = V_{1,2}/c$.

To support the stationary configuration moving as a whole, the relationship (1) between the angles $\gamma_{1,2}$ and soliton speeds should be met, and from Eq. (10) we have:

To compare Eq. (14) with the exact solution, it should be remembered that, as mentioned, in Figure 4 the direction of motion of the whole patterns is not known {a priori} and should be found, whereas in Section 2 it was assumed that the pattern moves along the $x'$-axis. On the other hand, the angles between the soliton fronts are invariant to the direction of the drift. This direction is defined by Eq. (2) in which (14) should now be used.

Consider first the configuration shown in Figure 4a. For the parameters shown in the caption to Figure 4a, from Eq. (10) we find $V_{1} = 1.004$; $V_{2} = 1.213$, so that $V_{2}/V_{1} = 1.208$. The solitons propagate at the following angles to the $x$-axis: $\varphi_{1} = \arctan(l_{1}/k_{1}) = -5.2\mbox{°}$ and $\varphi_{2} = \arctan (l_{2}/k_{2}) = 4.7\mbox{°}$. The same angles soliton fronts constitute with the $y$-axis (see Figure 3), therefore, the angle between the soliton fronts is $y =|\varphi_{1}| + \varphi_{2} = \gamma_{1} + \gamma_{2} = 9.9\mbox{°}$. Combining this relationship with Eq. (2), we find $\gamma_{1} = 52.3\mbox{°}$, $\gamma_{2} = - 42.4\mbox{°}$.

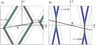Figure 6

The direction of the pattern drift is determined by the angle $\delta = \varphi_1 + \gamma_1 = \varphi_2 - \gamma_2 = 47.1\mbox{°}$, and the speed of drift is $U = V_{1} / \cos\gamma_{1} = 1.643$. This direction is shown by a black line with the arrow in Figure 6a together with the exact two-soliton solutions, at the two moments of time, $t = -75$ and $t = 75$. As one can see, the kinematic description completely agrees with the exact solution and, moreover, predicts correctly the pattern velocity in the $x,y$-plane.

Note that in the coordinate frame co-propagating with the pattern velocity $\mathbf{U}$ (along the black line in Figure 6), the pattern is stationary, and the two-soliton solution in this frame is a function of only spatial variables. This can be confirmed by the change of variables in the exact solution (5), (12): $x = \xi \cos\delta - \eta \sin \delta$ and $y = \xi \sin \delta + \eta \cos \delta$. Rotating the coordinate frame by the angle $\delta$ determined above, we obtain the stationary moving two-soliton pattern in coordinate $\xi, \eta$.

The same calculations can be carried out for the pattern shown in Figure 4b. Using the parameters shown in the figure caption, we find again from Eq. (10) $V_{1} = 0.045$; $V_{2} = 0.041$, so that $V_{2}/V_{1} = 0.912$. The solitons propagate at the angles to the $x$-axis: $\varphi_{1} = \arctan(l_{1}/k_{1}) = -10.8\mbox{°}$ and $\varphi_{2} = \arctan(l_{2}/k_{2}) = 9.8\mbox{°}$. The angle between the soliton fronts is $\gamma = |\varphi_1| + \varphi 2 = \gamma_1 + \gamma_2 = 20.6\mbox{°}$. Combining this relationship with Eq. (2), we find $\gamma_{1} = -3.9\mbox{°}$, $\gamma_{2} = 24.5\mbox{°}$.

The direction of the pattern drift is determined by the angle $\delta = \varphi_1 + \gamma_1 = \varphi_2 - \gamma_2 = -14.71\mbox{°}$, and the speed of the drift is $U = V_{1} /\cos \gamma_{1} = 0.046$. This direction is shown by the black line in Figure 6b) together with the exact two soliton solutions (12) and (5) at two time moments, $t = -1.5 \times 10^{4}$ and $t = 1.5 \times 10^{4}$. This figure illustrates again a good agreement between the kinematic description and exact solution of KP2 equation.

For the triad configurations shown in Figure 5, the parameters are very close to those specified in the caption to Figure 4, therefore the directions and speeds of the pattern motion are also very close to those presented above and shown in Figure 6.

4.1. On the Observed Multisoliton Structures on a Shallow Water

As mentioned above, the two-dimensional configurations of interacting surface-wave solitons were observed both in the laboratory and over a flat bottom in shallow beach sea areas. In particular, in Ref. [Ablowitz and Baldwin, 2012] from which the photos shown in Figure 1 were taken, the authors, using the dimensionless KP2 equation, have demonstrated that its exact solutions can qualitatively represent a very similar structures as frequently observed wave patterns. The KP2 equation in that paper is equivalent to our Eq. (4) with $\alpha = 6$, $\beta = 1$, $c = 6$, and the dimensionless parameters $k_{i}$ and $P_{i} \equiv l_{i} /k_{i}$ were used to mimic the patterns presented in the photos taken in the different areas of Eastern Pacific with the water depth between $h = 5$ cm and 20 cm. We applied the developed concept to the several cases presented in [Ablowitz and Baldwin, 2012] using the expression for the soliton amplitude, $A_{s} = 3 \beta k^{2} /\alpha$ (see the formula after (9)). Then, the speeds of the interacting solitons, and finally, the speed and direction of the drift of the whole pattern with respect to the $x$-axis were found. After that, we have estimated the real solitary wave parameters using the scaling to the dimensional physical variables for the average water depth $h = 15$ cm. As the result, we have obtained that in the different cases shown in [Ablowitz and Baldwin, 2012], the amplitudes of solitons range from 7.5 cm to 30 cm, and their velocities, from 1.72 m/s to 2.94 m/s, whereas the linear long-wave velocity is $c_{0} = 1.21$ m/s. These values are beyond the limits of validity of the KP2 equation which is applicable to the weakly nonlinear wave perturbations (note that one of the solitary waves shown in Figure 1 is, apparently, breaking). Besides, the angles between the directions of soliton propagation and the $x$-axis in the KP2 equation are not small that also contradicts to the applicability of the KP2 equation. Thus, to quantitatively describe the interesting and rather ubiquitous multisoliton patterns of large amplitudes in shallow basins, another, strongly nonlinear models are necessary.

5. Application of the Kinematic Approach to the 2D Benjamin-Ono Equation

5.1. Theoretical Formulation

When the stratification in the deep ocean is such that one of the layers is thin in comparison with the wavelength of internal wave, the basic equation describing long weakly nonlinear waves is the Benjamin-Ono (BO) equation; its 2D version derived in Refs. [Grimshaw, 1981; Grimshaw and Zhu, 1994; Matsuno, 1998; Tsuji and Oikawa, 2001] is:

where the symbol $\wp$ stands for that the principal value of the integral should be considered and the expression for the coefficients $c$, $\alpha$, and $\beta$ can be found in the papers cited above. Unlike the one-dimensional version, this equation is non-integrable.

This equation has a single solitary solution representing a plane wave obliquely propagating at an angle to the $x$-axis:

where

The soliton amplitude is determined solely by the parameter $k$: $A = 4 \beta k/\alpha$, whereas its speed $V = (V_{x}^{2} + V_{y}^{2})^{1/2}$ (in the reference frame moving with the velocity $c_{0}$ in which equation (15) is written) depends both of $k$ and $l$:

For the components of the soliton velocity the formulae are the same as in Eq. (11).

The exact two-soliton solution representing two plane waves propagating at an angle to each other is unknown, whereas in 1D case the BO equation is completely integrable and has $N$-soliton solutions (see, e.g., [Ablowitz and Segur, 1981; Matsuno, 1979, 1980]). Soliton interaction in the 2D case was studied in Ref. [Matsuno, 1998] by means of the asymptotic approach and numerically in Ref. [Tsuji and Oikawa, 2001], however nether the direction, nor the speed of the pattern propagation were studied in those papers.

The kinematic approach developed in Section 4 yields that the direction of the pattern drift is determined by the angle $\delta = \varphi_{1} + \gamma_{1} = \varphi_{2} - \gamma_{2}$, and the speed of the drift is $U = V_{1} /\cos \gamma_{1}$, where $\varphi_{1} = \arctan(l_{1}/k_{1}$) is the angle between the direction of motion of one of the solitons with the $x$-axis, and $\gamma_{1}$ is the angle between its front and the perpendicular to the direction of motion which is determined by Eq. (2). Thus, again with the help of the kinematic approach we can determine the direction and speed of motion of two-soliton pattern if we know the parameters of individual BO solitons, $k_{1,2}$ and $l_{1,2}$, although the front shifts cannot be determined from this approach. The attempt to determine the front shifts was undertaken by Matsuno [1998] on the basis of an asymptotic theory. We are currently developing an alternative asymptotic theory to derive the front shifts; the result will be published elsewhere.

5.2. Internal Waves in the Two-Layer Benjamin-Ono Model

A typical application of the BO equation is related to the oceanic internal waves. In many observations, the water stratification is close to the two-layer, including the cases when the thickness $ h$ of the upper layer is much smaller than the total depth $H$. If the characteristic length $\lambda$ of internal waves is such that $h \ll \lambda\ll H$, then the wave can be described by the 2D BO equation (15). In the latter, for the two-layer model, $ \eta (x, y, t)$ stands for the displacement of a pycnocline, and the coeffcients of Eq. (15) in the Boussinesq approximation are (see, e.g., [Apel et al., 2007]):

where $c_{0}$ is the linear long wave speed, $\delta \rho/ \rho$ is the relative density difference between the layers, and $g$ is the acceleration due to gravity.

Here, we apply the kinematic approach to the observational data presented for the Case A in [Wang and Pawlowicz, 2012] for internal waves in the Strait of Georgia, Canada (see Figure 2 above). The stratification in the Strait was indeed close to two-layer with the thickness of the upper layer $h \approx 5$ m, $ \delta \rho / \rho\approx 0.014$, and the total average depth $H = 150$ m. With such parameters, one can readily estimate the speed of long linear waves on the pycnocline, $c_{0} = 0.82$ m/s, and the coefficients (15) of nonlinearity, $\alpha = - 0.246$ s$^{-1}$ and dispersion $\beta = 2.048$ m$^{2}$/s. Below we follow the authors' presumption that the observed pattern represents the interaction of two solitary waves, whereas in such a case, the post-interaction western front in Figure 2b should be parallel to the eastern front, as shown by the green line with the upper index T.

The amplitudes of solitary waves estimated in that paper with the eastern and western fronts were equal approximately $\widetilde{A}_{1,2} = -3.3$ m. The directions of front motion are shown in Figure 2b) above: $\varphi_{1} = -60\mbox{°}$ and $\varphi_{2} = 23\mbox{°}$ with respect to the $x$-axis, so that the angle between the wave fronts is $\gamma = 83\mbox{°}$. Using these data and the relationship between the soliton amplitude and parameter $k, A = 4 \beta k/\alpha$ (see the formula after (17)), we find for the western front in Figure 2b): $k_{1} \approx 0.1$ m$^{-1}$, $l_{1} = k_{1} \cdot \tan (\varphi_{1}) \approx -0.171$ m$^{-1}$ and for the eastern front, $k_{2} = k_{1} \approx 0.1$ m$^{-1}$, $l_{2} = k_{2} \cdot \tan(\varphi_{2}) \approx 0.042$ m$^{-1}$. These parameters allow one to estimate the characteristic widths of solitary waves, $\Lambda_{i} = 1/(k_{i}^{2} + l_{i}^{2})^{1/2}$: $\Lambda_{1} \approx 5.05$ m, $\Lambda_{2} \approx 9.3$ m. Then, using Eq. (18), we find that $V_{1} \approx 0.72$ m/s, $V_{2} \approx 0.26$ m/s. The speed of a soliton front in the immovable reference frame is given by the formula:

which yields for the western front $\widetilde{V_{1}} = 1.33$ m/s and for the eastern front, $\widetilde{V_{2}} = 1.06$ m/s. These values agree with data presented in Figure 9 of [Wang and Pawlowicz, 2011].

Now, using Eq. (2), we find the angles between the soliton fronts and the normal to the direction of the whole pattern drift, $\gamma_{1} = 34.2\mbox{°}$ and $\gamma_{2} = 131.2\mbox{°}$. This allows one to find the speed of the whole pattern drift, $\widetilde{U} = 1.61$ m/s, as well as the direction of its motion with the angle $\delta = -25.8\mbox{°}$ to the $x$-axis. The corresponding velocity vector $\widetilde{{\mathbf U}}$ is shown by the red arrow in Figure 2b. Dashed red line labelled "Norm" shows the axis normal to vector $\widetilde{{\bfseries U}}$.

We have also estimated the parameters of the bridge between the solitary wave fronts (the "merge front" in Figure 2b. Given the angle of the bridge $\varphi_{3} = -4\mbox{°}$ with respect to the $x$-axis (see Figure 2b and using Eqs. (2) and (3), we find its speed and amplitude $\widetilde{V}_{3} \approx 1.49$ m/s, $\widetilde{A}_{3} \approx -11$ m, respectively; the corresponding parameters $k_{3}$ and $l_{3}$ are: $k_{3}\approx 0.329$ m$^{-1}$, $l_{3} \approx -0.023$ m$^{-1}$, and the characteristic width of the bridge $\Lambda_{3} \approx 3$ m.

However, there is again a certain disagreement between small-angle approximation on which the 2D BO equation (15) is based, and the observed pattern where the angles between the soliton fronts are not small. On the other hand, since in this case the soliton amplitudes are known from the measurements, the velocities of solitons can be obtained independently from the corresponding one-dimensional BO equation in which the direction $x$ is normal to the given soliton. Thus, instead of Eq. (18), we let $V_{1,2 } = c_{0} + \alpha A_{1.2}/4$ and, respectively, $\Lambda_{1,2} = 4 \beta / \alpha A_{1,2}$. Then, we find that the speeds of soliton fronts in the immovable coordinate frame are $V_{1} \approx 0.94$ m/s and $V_{2} \approx 1$ m/s. Using Eq. (2), we find the angles between the soliton fronts and the normal to the direction of the whole pattern drift, $\gamma_{ 1 } = 43.9\mbox{°}$ and $\gamma_{2} = 39.1\mbox{°}$. This allows to find the speed of the whole pattern drift, $U_{1} = 1.3$ m/s, as well as the direction of its motion with the angle $\delta = -16.1\mbox{°}$ to the $x$-axis. Vector ${\mathbf{U}}_{1}$ is shown in Figure 2b) by black arrow.

The parameters of the bridge between the solitary wave fronts can be estimated in a similar way. Given the angle of the bridge $\varphi_{3} = -4\mbox{°}$ to the $x$-axis (see Figure 2b) and using Eqs. (2) and (3), we find first the angle between the bridge front and new normal to the drift velocity, $\gamma_{3} = -12.1\mbox{°}$. Then, the bridge speed and amplitude are $V_{3} \approx 1.27$ m/s and $A_{3} \approx -7.36$ m, respectively; the parameters $k_{3} \approx 0.221$ m$^{-1}$, $l_{3} \approx -0.015$ m$^{-1}$, and the characteristic width of the bridge is $\Lambda_{3}\approx 4.53$ m.

These results differ, albeit not very strongly, from those using the 2D BO equation (for example, the drift directions differ by $9.7\mbox{°}$). The direct approach is simpler and supposedly more reliable, and it is recommended in the cases when solitons amplitudes are known from the experiment.

6. Conclusion

In this paper we have suggested a simplified kinematic description of the two-dimensional patterns of obliquely interacting solitary waves. This approach is applicable to solitons in any model, including those described by non-integrable and not necessarily weakly nonlinear equations. To validate the suggested approach, we compared it with the analytical results of the integrable KP2 equation, the only two-dimensional physical model for which the exact solution is known for now. The developed method allows one to calculate directions and speeds of the entire wave pattern propagation, including the cases of resonant configurations. As an application, we have considered the observational data for the internal waves on the interface between two layers [Wang and Pawlowicz, 2012] using the kinematic approach for the 2D BO model, and, more directly, using the soliton velocities valid at any propagation angles. We also have evaluated multisoliton pattern parameters within the dimensionless KP2 equation suggested in [Ablowitz and Baldwin, 2012] for the modelling of the observed patterns in the shallow sea areas, and briefly discussed the problems arising due to the strong nonlinearity and large angles between the soliton fronts.

In the future, we hope to extend the kinematic approach to the consideration of more complicated problems that, in our opinion, are not sufficiently clarified in the existing literature. One of such problems is the description of non-stationary dynamics of obliquely interacting solitons; another is calculation of phase shifts in the non-integrable models. The approach can be further developed for the application to surface and internal waves described, for example, by the 2D Gardner equation, Boussinesq set of equations, and other model equations used not only in the fluid mechanics.

Acknowledgments

References

Ablowitz, M. J., D. E. Baldwin (2012) , Nonlinear shallow ocean-wave soliton interactions on flat beaches, Phys. Rev. E, 86, p. 036305, https://doi.org/10.1103/PhysRevE.86.036305.

Ablowitz, M. J., H. Segur (1981) , Solitons and the Inverse Scattering Transform, 425 pp., SIAM, Philadelphia, https://doi.org/10.1137/1.9781611970883.

Anker, D., N. C. Freeman (1978) , Interpretation of three-soliton interactions in terms of resonant triads, J. Fluid Mech., 87, no. 1, p. 17–31, https://doi.org/10.1017/S0022112078002906.

Apel, J. R., L. A. Ostrovsky, Y. A. Stepanyants, et al. (2007) , Internal solitons in the ocean and their effect on underwater sound, J. Acoust. Soc. Am., 121, p. 695–722, https://doi.org/10.1121/1.2395914.

Grimshaw, R. (1981) , Evolution equations for long nonlinear internal waves in stratified shear flows, Stud. Appl. Math., 65, p. 159–188, https://doi.org/10.1002/sapm1981652159.

Grimshaw, R., Y. Zhu (1994) , Oblique interaction between internal solitary waves, Stud. Appl. Math., 92, p. 249–270, https://doi.org/10.1002/sapm1994923249.

Kadomtsev, B. B., V. I. Petviashvili (1970) , On the stability of solitary waves in weakly dispersive media, Sov. Phys. Doklady, 15, p. 539–541.

Matsuno, Y. (1979) , Exact multi-soliton solution of the Benjamin-Ono equation, J. Phys. A, 12, p. 619–621, https://doi.org/10.1088/0305-4470/12/4/019.

Matsuno, Y. (1980) , Interaction of the Benjamin-Ono solitons, J. Phys. A, 13, p. 1519–1536, https://doi.org/10.1088/0305-4470/13/5/012.

Matsuno, Y. (1998) , Oblique interaction of interfacial solitary waves in a two-layer deep fluid, Proc. R. Soc. Lond. A, 454, p. 835–856, https://doi.org/10.1098/rspa.1998.0188.

Maxworthy, T. (1980) , On the formation of nonlinear internal waves from the gravitational collapse of mixed regions in two and three dimensions, J. Fluid Mech., 96, no. 1, p. 47–64, https://doi.org/10.1017/S0022112080002017.

Miles, J. W. (1977a) , Obliquely interacting solitary waves, J. Fluid Mech., 79, no. 1, p. 157–169, https://doi.org/10.1017/S0022112077000081.

Miles, J. W. (1977b) , Resonantly interacting solitary waves, J. Fluid Mech., 79, no. 1, p. 171–179, https://doi.org/10.1017/S0022112077000093.

Newell, A. C., L. G. Redekopp (1977) , Breakdown of Zakharov–Shabat theory and soliton creation, Phys. Rev. Lett., 38, p. 377–380, https://doi.org/10.1103/PhysRevLett.38.377.

Satsuma, J. (1976) , Soliton solution of the two-dimensional Korteweg-deVries equation, J. Phys. Soc. Japan, 40, no. 1, p. 286–290, https://doi.org/10.1143/JPSJ.40.286.

Small, J. (2002) , Internal tide transformation across a continental slope off Cape Sines, Portugal, J. Marine Systems, 32, p. 43–69, https://doi.org/10.1016/S0924-7963(02)00029-5.

Tsuji, H., M. Oikawa (2001) , Oblique interaction of internal solitary waves in a two-layer fluid of infinite depth, Fluid Dyn. Res., 29, p. 251–267, https://doi.org/10.1016/S0169-5983(01)00026-0.

Wang, C., R. Pawlowicz (2011) , Propagation speeds of strongly nonlinear near-surface internal waves in the Strait of Georgia, J. Geophys. Res., 116, p. C10021, https://doi.org/10.1029/2010JC006776.

Wang, C., R. Pawlowicz (2012) , Oblique wave-wave interactions of nonlinear near-surface internal waves in the Strait of Georgia, J. Geophys. Res., 117, p. C0631, https://doi.org/10.1029/2012JC008022.

Whitham, G. B. (1967) , Variational methods and applications to water waves, Proc. R. Soc. London, Ser. A, 299, p. 6–25, https://doi.org/10.1098/rspa.1967.0119.

Wiegel, R. L. (1964) , Oceanographical Engineering, Englewood Cliffs, N.J., Prentice-Hall.

Zakharov, V. E., S. V. Manakov, S. P. Novikov, L. P. Pitaevsky (1980) , Theory of Solitons: The Inverse Scattering Method, Nauka, Moscow (Engl. transl.: Zakharov, V. E., et al. (1984), Theory of Solitons, Consultant Bureau, New York.).

Received 8 June 2020; accepted 12 June 2020; published 12 July 2020.

 
Citation: Ostrovsky L. A., Y. A. Stepanyants (2020), Kinematics of interacting solitons in two-dimensional space, Russ. J. Earth Sci., 20, ES4007, doi:10.2205/2020ES000735.
 

Copyright 2020 by the Geophysical Center RAS.