RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 20, ES6016, doi:10.2205/2020ES000725, 2020
P. A. Shabanov1, N. N. Shabanova2
1Shirshov Institute of Oceanology RAS, Moscow, Russia
2Lomonosov Moscow State University, Moscow, Russia
An advanced methodology for the detection and quantification of the ice-free period in the Arctic coastal zone is proposed. Ice-free period (IFP) dynamics is analyzed in the Kara Sea coastal zone near "Marresalya" and "Amderma" stations using long-term satellite data about sea ice concentrations. In a new method an advanced approach for defining the IFP characteristics (starting/ending dates and duration) was applied in addition to the conventional use of 15% sea ice concentration threshold. We provide estimates of the mean statistics and linear trends in the IFP characteristics using three long-term satellite-based sea ice concentration datasets: OSI SAF, NSIDC, JAXA and compare them to the estimates based upon direct observations on stations. Mean IFP durations and ending dates as well as linear trends derived from satellite data show a close comparability with observations with differences ranging within 2–7 days for IFP durations and within 0.01–0.05 days/year for IFP ending date trends. At the same time, strong deviations were found for both mean and long-term trends of the IFP starting dates, specifically showing negative trends in the satellite-derived starting dates which is not confirmed by observations. This results in a moderate agreement on trend estimates in IFP durations between satellite data and observations, while the mean characteristics are in a very good agreement and implies the necessity of more careful look onto representativeness of satellite data in the near-coastal zone during the onset season.
Sea ice conditions play a great role in the coastal dynamics of the circumpolar Arctic [Ogorodov et al., 2016]. Sea ice limits the interaction between the land and seawater. Near-shore sea ice cover protects the coasts from wave and thermal impacts. Most of the coastline erosion occurs during relatively short ice-free period (or open water season). In many parts of the Arctic, the duration of ice-free period increased in recent decades [Peng et al., 2018]. This makes the ice-free period (IFP) an effective climate indicator, which is especially important for the coastal dynamics monitoring. Significant changes in the IFP characteristics (total duration, sea ice retreat/advance dates) greatly affect the coastal infrastructure, navigation, and coastal ecosystems. These impacts are also very relevant for the large natural and socioeconomic research programs in the North Eurasia, such as NEFI [Groisman et al., 2017].
Coastal retreat rates in Kara Sea depend on sea ice conditions. Waves affect coast provoking its' retreat during the IFP only. Changes in the ice-free period result in the changes in the coastal dynamics. However, monitoring of the duration of IFP is a complicated task due to a lack of observational data and highly variable sea ice conditions in the Arctic region.
Modern satellite datasets provide great opportunities for sea ice climate monitoring. Satellite sea ice products (extent, area, and concentration) are widely used for the analysis of ice conditions over open Arctic Ocean regions [Stroeve et al., 2006], however, they are still not extensively applied to the coastal studies [Barnhart et al., 2014] due to various uncertainties which are specific in the near-shore regions, for instance the signal contamination from the land. Thus, data pre-processing in the coastal zone requires the development of specific methods, enabling to quantify the uncertainties with the highest possible accuracy.
Sea ice concentration data could be used for estimating IFP characteristics. The most common way to estimate the IFP characteristics is the threshold approach. In this approach all pixels or grid nodes, involved in the estimation, with the values smaller than a threshold (set to 15% usually) are marked as "open water" [Peng et al., 2018]. This method is widely used by the polar ice cap researches [Howell et al., 2009] for calculation of the number of open water days [Khon et al., 2010].
Unfortunately, the threshold approach is very sensitive to the absolute data values. Sea ice concentration time series before 1987 (it is strongly linked to Scanning Multichannel Microwave Radiometer (SMMR) usage) demonstrate a complicated behavior. Also, coastal pixel data could be contaminated from land and show significant overestimation of sea ice concentration: in such time series concentrations are always greater than 30–40% even during summer IFP, while alternative sea ice cover observations show concentrations near zero values. Another important problem is that the pixel size is quite large, being 625 km$^2$ for 25 km spatial resolution. Also the total concentration (or sea ice extent/area) data include information not only from coastal zone, but from the open sea as well. Thus, moving ice, liquid water on the ice cover and polynyas considerably complicate the estimation of the absolute values [Dmitrenko et al., 2005; Reimnitz et al., 1994]. All these circumstances limit the application of the threshold method. We decide that sea ice concentration time series analysis should be also considered in.
We suggest here an alternative method for estimation IFP characteristics in the Arctic coastal zone. The results of application are examined using sea ice cover observations in the Kara Sea region (the western Yamal Peninsula and the western Yugorsky Peninsula).
 |
| Figure 1 |
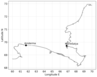
The study area includes the Kara sea coastal zone, near "Marresalya" (World Meteorological Organization (WMO) index 23032, 69.72° N, 66.80° E) and "Amderma" (WMO index 23022, 61.70° N, 69.75° E) meteorological stations. Station "Marresalya" (MS) is located on the western coast of the Yamal Peninsula, station "Amderma" (AM) is on the western coast of the Yugorsky Peninsula (Figure 1).
We will use sea ice cover observations available at these sites for 1979–2015. These observations will be used for validation of the IFP detection method developed in the study. Yamal Peninsula is a key region for the oil and gas offshore industry. Thus, understanding of the coastal dynamics conditions is relevant for the assessment of the stability of coastal infrastructure, impacts of its exploitation and regional sustainable development of the neighboring territories.
 |
| Table 1 |
Several gridded satellite sea ice concentration (SIC) datasets (highly processed data, levels L3–L4) available from OSI SAF, NSIDC, JAXA missions were used to define the IFP characteristics near "Marresalya" and "Amderma" points. Three datasets were used jointly to reduce the level of uncertainties in the data and to provide the ensemble estimates, which are expected to be more robust and accurate compared to the single estimates. Information about the employed SIC datasets is summarized in Table 1.
All analyzed datasets have daily temporal resolution. This resolution is optimal for IFP detection. All sea ice concentration time series were converted into the percentages (0–100%).
We used two OSI SAF (Satellite Application Facility on Ocean and Sea Ice) products: OSI-450 [OSI SAF, 2017] and OSI-430-b [Lavergne et al., 2019]. The OSI-450 product is the second version of the OSI SAF Global Sea Ice Concentration Climate Data Record (SIC CDR v2.0). The OSI-430-b product is the corresponding Interim CDR, an operational extension with a latency of 16 days. OSI-450 product provides a full reprocessing of sea ice concentration with improved algorithms and an upgraded processing chain, covering the period 1979 to 2015. The sea ice concentration is computed from the SMMR (1979–1987), SSM/I (1987–2008), and SSMIS (2006–2015) instruments, as well as from ECMWF ERA-Interim data. The OSI-430-b product extends the OSI-450 dataset from 2016 onwards. It uses SSMI/S data from NOAA CLASS, and also operational analysis and forecasts from ECMWF. In all other respects the same processing chain and algorithms are used for OSI-450 and OSI-430-b, products, thus ensuring temporal consistency between the products.
NSIDC (National Snow & Ice Data Center) provides various sea ice datasets. We used Climate Data Record (CDR) of sea ice concentration from the passive microwave data [Meier et al., 2017; Peng et al., 2013]. The CDR algorithm output is a rule-based combination of ice concentration estimates from the two well-established algorithms, namely the NASA Team (NT) algorithm [Cavalieri et al., 1984] and the NASA Bootstrap algorithm [Comiso, 1986].
JASMES (JAXA Satellite Monitoring for Environmental Studies) sea ice concentration product, distributed by JAXA (Japan Aerospace Exploration Agency), in terms of pre-procession follows the technology used in NSIDC CDR dataset: it also uses Polar Stereo projection with 25 km spatial lag [JASMES, 2019]
 |
| Figure 2 |
 |
| Figure 3 |
To smooth the uncertainties from nearshore data, grid points/pixels within 35 km radii around the sites "Marresalya" and "Amderma" were used for co-location with each SIC dataset. Within the 35-km circle we computed median values which were further used for building time series. All time series were also additionally smoothed by a 15-day median filter (Figure 2 and Figure 3) to exclude sub daily outliers. Using datasets with different post-processing algorithms allowed for more accurate and robust estimation of IFP characteristics.
To overcome the shortcomings in the threshold method [Comiso, 1984; Farquharson et al., 2018; Meier and Stroeve, 2008] we suggest here a new approach for quantifying IFP. The main idea is to combine the advantages of the threshold method with consideration of gradients characterizing seasonal loss/gain.
The original advanced threshold approach (ATA) allows for determining IFP characteristics such as duration and starting/ending dates from the SIC annual variation analysis. To determine duration ($D$), the starting date $(S)$ and the ending date $(E)$ of the IFP should be calculated. IFP starting date is searched within the period from the 1st of March till the 15th of September. In some specific cases valid IFP ending dates may not be necessarily observed before the end of the current calendar year, especially for the western Kara Sea coastal zone. Thus, the search period for the ending dates is extended: the search is applied over the period from the 15th of September to the 1st of March of the next calendar year.
SIC time series within each sub-period are normalized to avoid the impact of the absolute values corresponding to the threshold. Then the SIC gradients are calculated for 28-days time slices. These slices roll out over the whole period with 1-day time step. Gradients are calculated as a difference between the last and the first slice elements. Only non-gappy slices consisting of values which are lower/greater (starting date/ending date) than threshold is considered. Following [Peng et al., 2018], the threshold was set to 15%. Then the slice with the maximum gradient is chosen and the last/first slice element is interpreted as the IFP starting/ending date respectively. The width of the running window can be considered as the representative melting/freezing period, corresponding to the period, when significant changes (melting or freezing) are observed in sea ice concentrations data record. The tests applied show that the optimal (in terms of Root Mean Squared Errors, RMSE) window width closely matches 28 days.
New ATA-like method was applied to the three satellite-derived sea ice concentration datasets which were used for estimation of ice-free period characteristics over the Kara Sea coastal zone (near "Marresalya" and "Amderma" stations). Here we are focused on revealing a relationship between IFP characteristics obtained from calculations and from observations. Ensemble approach (based on medians estimated within datasets values) is also considered, because it provides more accurate and robust estimates of IFP [Shabanov and Shabanova, 2019].
Applying the ATA method to the SIC time series, we calculate IFP starting/ending dates and total duration for the period 1979–2018. The method skills were first analyzed by applied simple qualitative metrics which in most cases demonstrated very good agreement. To further validate the method skills quantitatively, we calculated statistical measures such as linear regression coefficients and RMSE using observations.
According to observations, the mean IFP duration $(D)$ at "Marresalya" is estimated at $114 \pm 15$ days for the 1979–2015 period. The historical extrema for IFP duration were observed in 1999 (85 days) and 2012 (147 days). Mean starting date is near the 29th of June $\pm 15$ days with extrema being observed at the 9th of June 2015 and at the 25th of July 1999. The mean values of the IFP ending dates are observed near the 22nd of October $\pm 11$ days with extrema detected at the 3rd of October 2013 and at 14th of November 2010.
According to the observations at station "Amderma", the mean IFP duration is $140 \pm 29$ days for 1979–2015 period. The historical extrema for IFP duration were observed in 1998 (66 days) and 1995 (220 days) years. Mean starting date is quantified to be near the 20th of June $\pm \;29$ days with extrema being observed at the 27th of March 1995 and at the 22th of July 1979. The mean IFP ending date is quantified being near the 7th of November $\pm \,18$ days with extrema observed at the 11th of September 1998 and 29th of December 2012.
 |
| Table 2 |
Extended coverage of the IFP statistics, obtained from satellite-based SIC datasets using ATA method is summarized in Table 2. Further, ensemble estimates will be considered in comparison with observations.
Mean IFP duration estimates based on ensemble values show good consistency with the observations, implying 114/107 days (observations / ensemble mean) at station "Marresalya" and 140/138 days at station "Amderma". Standard deviations and min-max range of the estimates revealed from satellite data sets are generally higher compared to observational values.
IFP mean starting date as revealed from satellite data differs from observational estimate by $\sim 2.5$ weeks (18 days) at station "Marresalya" and by $\sim 3$ weeks (21 days) at station "Amderma". This can be ranked as a great difference which is likely due to an improper accounting for the complicated conditions during the ice melting season. Robust estimates of sea ice concentration from satellite measurements are typically available with some delay compared to the in-situ coastal observations. For most characteristics, however, we find a very high agreement between satellite-based and observation-based statistics. Neither dataset shows significant advantages implying being superior compared to the others.
The mean estimates of IFP ending date differ from observations by $\sim 1$ week at station "Marresalya" and by 2.5 weeks (17 days) at station "Amderma". This difference is smaller, than for IFP starting date because of a more robust seasonal increments of the ice period. At the same time, observational minima are smaller than those calculated from the satellite data. This can be interpreted as the impact of the local coastal processes (e.g. effect of moving sea ice) influencing on the estimates when the satellite data need more time to detect in a robust manner the nearest to the site pixel as "sea ice". On one hand, this difference between local observations and area-averaged estimates does complicate comparison and interpretation. On the other hand, this allows us a variety of information about sea ice conditions in the coastal zone.
According to the observations, estimates of linear trends for 1979–2015 at station "Marresalya" show statistically significant ($p_{\mathrm{value}}<0.01)$ upward tendencies for the most of parameters: $-0.42$ days/year for $S$; $+0.36$ days/year for $E$ ($p_{\mathrm{value}}<0.05)$ and $+0.78$ days/year for $D$ respectively. Shifts in both time limits (due to the earlier ice retreat and the delayed ice advance) are thus indicative, resulting in significant increase of the IFP duration at "Marresalya" on the western Yamal Peninsula.
A strong delay in the ice advance $(E)$ is observed on the western coast of the Yugorsky Peninsula, at station "Amderma", it is estimated at $+0.70$ days/year. Linear tendency in the ice-free period starting date is statistically insignificant being $-0.17$ days/year for 1979–2015. The overall IFP duration $(D)$ shows an increase of 0.87 days/year ($p_{\mathrm{value}}<0.05)$.
Thus long-term changes over the western Kara Sea are characterized by similar statistically significant trends in the IFP duration and the starting/ending date parameters with both showing negative trends in starting date, while the trend is insignificant for "Amderma", and statistically significant for "Marresalya".
 |
| Figure 4 |
 |
| Figure 5 |
 |
| Table 3 |
 |
| Table 4 |
Computed linear trend coefficients ($A_{\mathrm{coef}}$ in Table 3) and RMSE of the IFP characteristics from ATA method applied to satellite datasets are shown in Table 4. The IFP duration time series derived from SIC datasets using both ATA and observations are presented in (Figure 4 and Figure 5).
Compared to observational tendencies, linear trends of the IFP characteristics based on ensemble values show quite an adequate agreement, especially in for the ending dates tendencies: 0.7/0.75 days/year at "Amderma" and 0.36/0.37 days/year at "Marresalya" for observations/ensemble data. For both sites tendencies derived from satellite data demonstrate statistically significant increase in IFP duration with the rates exceeding those reported by observations. For station "Amderma" trend estimates from the satellite ensemble data are twice as large compared to the observations being 2.17 and 0.87 days/year respectively. On the other hand, tendencies in the starting dates estimated from SIC datasets show significantly stronger negative trends compared to observations being $-1.06$ vs $-0.17$ at station "Amderma" and $-0.78$ vs $-0.42$ at station "Marresalya". This can be explained by the lack or lower accuracy of satellite data compared to observations in the coastal zone. However, the rapid sea ice changes in the southmost regions of the Arctic are captured by the satellite measurements even in the nearshore zone. Also important, that insignificant negative trends in the IFP ending dates at station "Amderma" in the SIC datasets are found to be significant in the satellite data. This can be interpreted as "The False Positive Bias" and may put some concerns on the Arctic climate change rates. For the present, it looks like that sea ice starts to melt earlier, however the tendency is not really drastic on the western coast of Yugorsky Peninsula.
 |
| Figure 6 |
 |
| Figure 7 |
As a result, the uncertainties in the estimate of IFP starting date play a critical role in determining the IFP duration using satellite SIC datasets. For both analyzed sites strong negative tendencies in the IFP starting dates result into the strong positive trends in the IFP durations. Using the ATA method, we analyzed IFP starting/ending dates in the SIC time series and found the consistency between estimates of the dates and the timing of sea ice melting/freezing season for both sites (Figure 6 and Figure 7). To estimate the accuracy of the calculated IFP characteristics we used RMSE derived from observations (Table 4). Estimates of RMSE at station "Marresalya" are lower than those at "Amderma", especially for ending dates $(E)$ for which the differences of 4–7 days were found. Estimates of RMSE for the duration and starting date range from 21–28 days for both "Marresalya" and "Amderma" stations. Relatively high RMSE values at both sites imply strong variability in IFP characteristics and also hint on the limitations on the use of observations for validation of satellite-based datasets. Thus, there is a fundamental difference between the estimates derived from SIC datasets and from observations.
We developed an advanced threshold approach (ATA) for an accurate detection and quantification of the IFP characteristics using satellite-derived sea ice concentration datasets. Comparison with observations from the western coast of the Yugorsky Peninsula ("Amderma") and the western coast of the Yamal Peninsula ("Marresalya") show a reasonable agreement for the IFP mean duration and for the long-term trends in the ending dates. Despite quite an adequate results of validation of IFP duration and ending dates, derived from SIC IFP starting dates demonstrate strong biases in both means and long-term trend estimates. Considering different SIC data sets, we found that neither SIC dataset is superior in revealing IFP characteristics compared to observations. In this respect ensemble approach engaging the use of different independent SIC datasets provides robust estimates, while for selected parameters of IFP individual datasets might be more accurate than those derived from ensembles. In this respect the ensemble approach is quite effective for selecting the most accurate dataset for estimating IFP parameters.
Suggested ATA method largely extends the capabilities of estimation of IFP parameters, as it accounts not only for the absolute values and pre-defined thresholds, but also for the timing of the intense melting and freezing of seasonal sea ice. In this respect various satellite sea-ice concentration data provide an opportunity to monitor the IFP characteristics along Arctic coastal zone and to develop objective records of IFP characteristics. We note that direct comparisons of satellite-based estimates with observations in the coastal zones may suffer from the uncertainties in satellite data in the near-shore. In this respect interpretation of these comparisons should be done in the context of spatial scales and different processes affecting sea ice dynamics locally and regionally.
Barnhart, K., I. Overeem, R. Anderson (2014) , The effect of changing sea ice on the physical vulnerability of Arctic coasts, Cryosphere, 8, p. 1777–1799, https://doi.org/10.5194/tc-8-1777-2014.
Cavalieri, D., P. Gloersen, W. Campbell (1984) , Determination of sea ice parameters with the NIMBUS 7 SMMR, J. Geophys. Res., 89, no. D4, p. 5355–5369, https://doi.org/10.1029/JD089iD04p05355.
Comiso, J., H. Zwally (1984) , Concentration gradients and growth/decay characteristics of the seasonal sea ice cover, Journal of Geophysical Research: Oceans, 89, no. C5, p. 8081–8103, https://doi.org/10.1029/JC089iC05p08081.
Comiso, J. (1986) , Characteristics of arctic winter sea ice from satellite multispectral microwave observations, Journal of Geophysical Research, 91, no. C1, p. 975–994, https://doi.org/10.1029/JC091iC01p00975.
Dmitrenko, I., K. Tyshko, et al. (2005) , Impact of flaw polynyas on the hydrography of the Laptev Sea, Global Planet. Change, 48, p. 9–27, https://doi.org/10.1016/j.gloplacha.2004.12.016.
Farquharson, L. M., D. H. Mann, et al. (2018) , Temporal and spatial variability in coastline response to declining sea-ice in northwest Alaska, Marine Geology, 404, p. 71–83, https://doi.org/10.1016/j.margeo.2018.07.007.
Groisman, P., et al. (2017) , Northern Eurasia Future Initiative (NEFI): facing the challenges and pathways of global change in the twenty-first century, Progress in Earth and Planetary Science, 4, p. 41, https://doi.org/10.1186/s40645-017-0154-5.
JASMES JAXA Satellite Monitoring for Environmental Studies. Polar Climate data (Sea Ice Concentration and Sea Ice Extent from 1978 to the present (2019)), JAXA. ftp://apollo.eorc.jaxa.jp/pub/JASMES/Polar _XXkm/ic0/climate/
Howell, S., C. Duguay, T. Markus (2009) , Sea ice conditions and melt season duration variability within the Canadian Arctic Archipelago: 1979–2008, Geophysical Research Letters, 36, p. 10, https://doi.org/10.1029/2009GL037681.
Khon, V., I. Mokhov, et al. (2010) , Perspectives of Northern Sea Route and Northwest Passage in the twenty-first century, Climatic Change, 100, no. 3–4, p. 757–768, https://doi.org/10.1007/s10584-009-9683-2.
Lavergne, T., A. M. Sorensen, et al. (2019) , Version 2 of the EUMETSAT OSI SAF and ESA CCI sea-ice concentration climate data records, Cryosphere, 13, p. 49–78, https://doi.org/10.5194/tc-13-49-2019.
Meier, W., J. Stroeve (2008) , Comparison of sea-ice extent and ice-edge location estimates from passive microwave and enhanced-resolution scatterometer data, Annals of Glaciology, 48, p. 65–70, https://doi.org/10.3189/172756408784700743.
Meier, W. N., F. Fetterer, M. Savoie, et al. (2017) , NOAA/NSIDC Climate Data Record of Passive Microwave Sea Ice Concentration, Version 3, NSIDC: National Snow and Ice Data Center, Boulder, Colorado USA, https://doi.org/10.7265/N59P2ZTG ([G02202], 04.03.2020).
Ogorodov, S., A. Baranskaya, et al. (2016) , Coastal dynamics of the pechora and kara seas under changing climatic conditions and human disturbances, Geography, Environment, Sustainability, 9, no. 3, p. 53–73, https://doi.org/10.15356/2071-9388_03v09_2016_04.
OSI SAF, (2017) , Global Sea Ice Concentration Climate Data Record v2.0 – Multimission, EUMETSAT SAF on Ocean and Sea Ice, Norwegian and Danish Meteorological Institutes, https://doi.org/10.15770/EUM_SAF_OSI_0008 (Online).
Peng, G., W. N. Meier, et al. (2013) , A long-term and reproducible passive microwave sea ice concentration data record for climate studies and monitoring, Earth Syst. Sci. Data, 5, p. 311–318, https://doi.org/10.5194/essd-5-311-2013.
Peng, G., M. Steele, A. Bliss, et al. (2018) , Temporal Means and Variability of Arctic Sea Ice Melt and Freeze Season Climate Indicators Using a Satellite climate data record, Remote Sens., 10, p. 1328, https://doi.org/10.3390/rs10091328.
Reimnitz, E., D. Dethleff, D. Nürnberg (1994) , Contrasts in Arctic shelf sea-ice regimes and some implications: Beaufort Sea versus Laptev Sea, Marine Geology, 119, p. 215–225, https://doi.org/10.1016/0025-3227(94)90182-1.
Shabanov, P. A., N. N. Shabanova (2019) , Open Water Season Changes Over the Kara Sea Coastal Zone: Marresalya Example, IEEE International Geoscience and Remote Sensing Symposium, p. 4218–4221, IGARSS, Yokohama, Japan, https://doi.org/10.1109/IGARSS.2019.8900056.
Stroeve, J., T. Markus, et al. (2006) , Recent changes in the Arctic melt season, Annals of Glaciology, 44, p. 367–374, https://doi.org/10.3189/172756406781811583.
Received 2 July 2020; accepted 7 July 2020; published 23 December 2020.


Citation: Shabanov P. A., N. N. Shabanova (2020), Ice-free period detection method in the Arctic coastal zone, Russ. J. Earth Sci., 20, ES6016, doi:10.2205/2020ES000725.
Copyright 2020 by the Geophysical Center RAS.