
RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 20, ES6008, doi:10.2205/2020ES000724, 2020
Valery G. Petrov1, Roman I. Krasnoperov2
1Pushkov Institute of Terrestrial Magnetism, Ionosphere and Radiowave Propagation RAS (IZMIRAN), Moscow, Troitsk, Russia
2Geophysical Center RAS (GC RAS), Moscow, Russia
One of the most widely used indices of geomagnetic activity is the $K$-index. It was proposed in 1938 by Julius Bartels as a measure of the influence of solar corpuscular radiation on the variations of the Earth's magnetic field. Among the essential requirements to indices of this type is its stationarity, i.e., stability of the rules by which it is calculated. Therefore, despite the known disadvantages of the $K$-index, it is still being calculated according to the method, proposed by Bartels. Historically, at Russian geomagnetic observatories, the $K$-index has been calculated using simplified methods. In this paper we compare the $K$-index calculation routine at Russian observatories with the standard $K$-index and planetary $Kp$-index calculation technique.
Indices of geomagnetic activity were designed to describe variations in the Earth's magnetic field induced by irregular causes [Mayaud, 1980; Zabolotnaya, 2007]. The $K$-index characterizes variations in the horizontal component of the geomagnetic field over a 3-hour time interval at a specific observatory, being a measure of the range of irregular and rapid, storm-time magnetic activity [Bartels, 1938; Bartels et al., 1939; Love and Remick, 2007]. It is a quasilogarithmic index (it increases by one unit with approximately double increase of amplitude) and takes values from 0 to 9 for each 3-hour interval of Universal Time. To calculate the index, variations of the geomagnetic vector $D$ and $H$ components (previously $Z$ was also used) are considered. The regular part ($Sr$) is subtracted from these variations and for each component in the remaining part the minimum and maximum values are determined. The maximum difference of these values is transferred into the $K$-index according to a special table, which is individual for each observatory. Thus, in order to calculate the $K$-index value, it is necessary to determine the scale and the regular part of variation $Sr$.
Bartels believed that the observed magnetic variations are divided into two parts – those induced by solar radiation that are not included in the $K$-index and magnetic field disturbances induced by particle precipitation. The latter were included in the $K$-index. Unfortunately, even now no clear and formal criteria for the division of these types of variations have been formulated. Initially, the technique for separating variations was gained experimentally through long practice and circulated within the observatory community at various seminars. In 1957 Bartels formulated the rules for calculating the $K$-index [Bartels, 1957], and then Mayaud in [Mayaud, 1967] generalized a detailed instruction for determining the $K$-index, which was adopted by the International Association of Geomagnetism and Aeronomy (IAGA). Nevertheless, the formulated rules remained only as general guidelines and observatory operators personal experience played a decisive role.
The $Sr$ variation, which is not considered by the $K$-index, is called the daily solar variation and, unlike the solar $Sq$ variation, which is determined for a whole month, determined for each day individually. Many observatories (in particular, almost all Soviet and now Russian) were not able to adopt the original methodology and used a simplified technique for $K$-index determination. According to the recommendations [Zabolotnaya, 2007] the $Sq$ variation was used instead of the $Sr$ variation. This does not correspond to the standard IAGA method that emphasizes that the $Sr$ variation must be calculated for each day individually and the use of $Sq$ variation, defined for the whole month, is unacceptable [Mayaud, 1967]. The necessity to determine $Sr$ for each day caused great difficulties in the development of computer methods for $K$-index determination. This issue was actively researched in 1970s and discussed at the special IAGA symposia.
During manual determination of the $K$-index using analog magnetograms, operator, based on his experience, corrects the obtained values by means of a special $Sq$ pallet, removing long-period trends in magnetic variations, considered beyond the $K$-index [Zabolotnaya, 2007]. This description, being not strict from the mathematical point of view, caused significant difficulties for the development of computer programs for $K$-index calculation. Mainly because the primary requirement to the $K$-index calculated by a computer program using digital data was its maximum similarity to the one, manually calculated by operator.
To solve this problem IAGA formed a special working group, which compared manual and various automated methods on a large geomagnetic dataset and recommended a few methods [Coles and Menvielle, 1991; Menvielle, 1991; Menvielle et al., 1995]. Programs that implement these methods are available at http://isgi. unistra.fr/softwares. php. It was shown that these methods do not alter the statistical properties of the $K$-index long-term distribution and do not distort the homogeneity of $K$-index timeseries. They were approved by the Working Group on Indices at the IAGA General Assembly in Vienna in 1991 as acceptable for practical use. The most popular method, based on linear estimation approach, was proposed by the Finnish Meteorological Institute (widely known as the "FMI-method") [Menvielle, 1990]. The other three methods are: Hermanus algorithm, developed at Hermanus Magnetic Observatory (South Africa) [Hattingh et al., 1989]; KASM-method, developed at the Institute of Geophysics, Polish Academy of Sciences (Poland) [Nowoyski et al., 1991]; and USGS-method, developed at the US Geological Survey (USA) [Wilson, 1987].
The scale for conversion of geomagnetic variations into the $K$-index value for any observatory is compiled using the same approach. The scale is built on the basis of the accepted minimum value for $K=9$, i.e. geomagnetic variations exceeding this threshold are assigned the value of $K=9$. This value is called the $K9$ limit. The upper limit of variation amplitude for K=0 is obtained by multiplying the lower limit of amplitude for $K=9$ by the coefficient 0.01. Amplitude limits for $K$ values from 1 to 8 points are obtained by multiplying the upper limit of amplitude of $K=0$ by coefficients: 2, 4, 8, 16, 24, 40, 64, 100. The preliminary value of the lower limit for $K=9$ is estimated based on the latitude of the observatory. Observatories, even those at the same latitude, may differ in the orientation of the magnetometers' sensors, intensity of induction current, etc. Due to the regional peculiarities of the observatory location, the relation between the observatory latitude and the scale is not well-defined by latitude and is finally determined only experimentally [Zabolotnaya, 2007].
The $K9$ limit threshold is finally determined after several years of the observatory operation by comparing the $K$-index values of a given observatory with the ones of the nearest observatories. It is assumed that the values of the $K$-index at any given time may differ from one observatory to another, but they all reflect the global geomagnetic disturbance and should provide the same statistical distribution of the geomagnetic variations over a long period of time. It is better to make such a comparison within a full solar cycle or at least during the years of maximum solar activity, when large $K$-index values are observed more often.
In addition to the $K$-index of individual observatories, a global or planetary magnetic disturbance index $Kp$ is calculated to estimate the overall state of the magnetic disturbance on a global scale from the data of 13 medium-latitude observatories. The method of its calculation is described in publications [e.g., Bartels, 1949; Menvielle and Berthelier, 1991] and we will not focus on it here.
Since there are no observatories with IAGA-approved $K9$ limit values for most of the Russian observatories, comparison with the planetary $Kp$-index will be made. In order to understand how the changes in the $K9$ limit are reflected in the statistical distribution of the $K$-index values, the $K$-index values for 2005–2016 were calculated for the $K9$ limit of 600, 650, 700 and 800 nT, based on the 1-minute data of the Borok observatory (BOX) [Chulliat and Anisimov, 2008]. The time interval was selected in the way so as to include the maximum and minimum years of the solar cycle.
 |
| Figure 1 |
Figure 1 shows the occurrence of different $K$-index values at $K9=500$ and 600 nT. The histogram shows that with the increasing accepted value of $K9$ also increases the number of cases with low $K$-index values (0 and 1), but the number of cases with the $K$-index values of 2 and higher, on the contrary, decreases. In this situation, the higher is the $K$ value, the more significant is this decrease. At $K=2$ the number of cases $K_{600}$ is less than the number of cases $K_{500}$ approximately by 5%, and at $K=6$ by 50%. The same pattern is observed when comparing K distribution with respect to other $K9$ values.
 |
| Figure 2 |
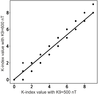
Figure 2 shows the connection of $K$-index values calculated with $K9$ equal to 500 and 600 nT. For this purpose, for each 3-hour interval, the value calculated with $K9=500$ nT was plot along the $X$-axis, while the $K$ value for the same moment calculated with $K9=600$ nT was laid off along the $Y$-axis. Apparently, there are not too many visible points on the chart, but in fact the total number of points on the chart reaches 35,000 (they just overlap each other). It is obvious that mathematical operations, like calculating the average, for $K$-index (which is a logarithm actually) do not make much sense, but the regression coefficient and average values have been calculated for the qualitative estimation of influence. The regression coefficient between values $K_{500}$ and $K_{600}$ is equal to 0.89, average value $K_{500}$ is equal to 2.17 and $K_{600}$ is 1.90. This result is quite natural, as with large $K9$ values the same magnetic field variation gives lower values of $K$-index and average value of $K$-index within the given data array.
 |
| Figure 3 |
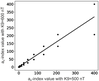
Figure 3 shows a similar chart, but instead of the $K$-index the $a_K$-index values are used. The $a_K$-index is a linear index that represents the normalized magnetic disturbance amplitude corresponding to the given $K$-index value for a conventional station with the limit $K9=250$ nT. Mathematical operations with $a_K$-index are physically feasible. The regression coefficient between the values of $a_{500}$ and $a_{600}$ is 0.80, the average value of $a_{500}$ is 12.09 and $a_{600}$ is 9.95. The average of eight daily values of $a_K$-index is $A_K$, which is the index, equivalent to the daily perturbation amplitude for a given observatory. $Ap$ is the linear equivalent to the planetary $Kp$-index.
Similar ratio is also observed with the comparison of $K$-index values calculated with other $K9$ limit. Generally, all these examples show a significant difference in the distribution of $K$-index values calculated with different $K9$ limits. The regression coefficients for $K$ and $a_K$-indices is less than one (0.89 and 0.80 respectively), average values of $K$ and $a_K$ also decrease with the increase of the $K9$ limit value. Thus, any of these approaches makes it possible to determine whether a given $K9$ limit value is overestimated or underestimated. Then which approach gives better result? The ratio of $K9$ limits was set as $500/600=0.83$, the regression coefficients are 0.89 and 0.86. The ratio of average $K$ values is 0.87 and the ratio of average $a_K$ values is 0.82. Thus, to calculate the new $K9$ limit value, the ratio of average $a_K$-index values gives the best estimate.
 |
| Figure 4 |
When calculating the $K$-index for the Borok observatory the limit value $K9=600$ nT was used. To validate this choice, the statistical distribution of the Borok $K$-index values was compared with the planetary $Kp$-index. Figure 4 presents a histogram of the distribution of occurrence of different values of the planetary $Kp$-index (black) and $K$-index for the Borok observatory calculated with the limit $K9=600$ nT (grey) for 2005–2016.
From the histogram we can see that the number of cases with $K=0$ at Borok observatory is much smaller than the number of cases when $Kp=0$. With $K>1$ the occurrence of the given $K$ value at Borok is always larger than the occurrence of the given $Kp$, and with increasing $K$ this ratio also increases. The average value of $K$ and $a_K$ indices for Borok (1.90 and 9.96 respectively) is noticeably larger than the corresponding values for the planetary indices $Kp$ and $Ap$ (1.60 and 8.41). The regression coefficient $Kp$ to $K_{\mathrm{BOX}}$ is equal to 1.066, and $Ap$ to $A_{\mathrm{BOX}}$ is equal to 1.02. All these data agree that the values of the $K9$ limit for the Borok observatory should be greater. It was shown above that the best estimate for the necessary $K9$ limit correction is the ratio of average values of the $a_K$-index. In this case, we get that the best correspondence between the Borok $K$-index with the $Kp$-index should be with the value of $K9=600 \times 9.96/8.41=710$ nT. To validate this new limit, the values of the $K$-index were calculated for the Borok observatory with the accepted $K9=700$ nT.
 |
| Figure 5 |
Figure 5 presents a histogram of the distribution of occurrence of different values of the planetary $Kp$-index and $K$-index for the Borok observatory, calculated with the limit value of $K9=700$ nT for 2005–2016. The difference between the distribution of $K_{\mathrm{BOX}}$ and $Kp$ has decreased with $K$ in the range of 2–4, while with $K>5$ it has practically disappeared. The difference between the average values of $K$ and $Kp$ (1.68 and 1.60, respectively) decreased, and the difference between the average values of $Ap$ and $a_K$ (8.41 and 8.40, respectively) also practically disappeared. With a further increase in the $K9$ limit, the difference between distributions and average values increases again. Thus, for the Borok observatory, the limit value of $K9=700$ nT ensures the best correspondence of the Borok $K$-index with the planetary $Kp$-index.
 |
| Table 1 |
A similar comparison has been made for several Russian observatories, for which representative series of continuous $K$-index values are available. The results are given in Table 1.
 |
| Figure 6 |
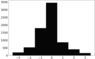
Table 1 was compiled by comparing the manually calculated $K$-index (except for Borok observatory) and the planetary $Kp$-index. At the same time, for all observatories, a much smaller occurrence of low values of the $K$-index (0, 1, and sometimes 2) as compared with the $Kp$-index was found. Sometimes this difference exceeded 100%. There could be 3 reasons for this difference: high level of industrial noise, incorrect choice of the $K9$ limit or inaccurate calculation of the $Sr$ variation. Figure 6 shows the difference between the values of the Moscow observatory (MOS) $K$-index calculated using one of the IAGA-approved programs, based on the FMI-method [Sucksdorff et al., 1991], and a simplified method based on the $Sq$ variation.
We can see that the error can reach 3 points and is not symmetric, the $K_{Sq}$ more often exceeds $K_{\mathrm{FMI}}$, i.e., on average, the use of the simplified method leads to a systematic overestimation of the $K$-index. The same result was obtained in [Anisimov et al., 2015; Mandrikova et al., 2012]. This effect, in general, is similar to the effect of the incorrect choice of the $K9$ limit. The use of $Sq$ variations is inevitable when calculating the $K$-index in real time, because all the IAGA-approved methods require data beyond the considered moment, which is not available in real time. However, the $K$-index calculated using $Sq$ variations instead of $Sr$ cannot be considered as the classical Bartels $K$-index and can only be used as a preliminary one. In IZMIRAN such indices are presented together with real time data (http://serv.izmiran.ru), but with a delay of 3–6 hours they are recalculated according to IAGA-approved methodology and only these indices are archived for further use (http://serv.izmir an.ru/out/KindMOS/Kind-mos.html).
The scales for calculating the $K$-index for most Russian observatories were determined in the 1930–40s. Comparison of $K$-indices calculated using these scales with the $Kp$ index shows that they need to be updated, and sometimes they are simply selected incorrectly. Thus, to ensure the comparability of the $K$-index of Russian observatories with the world network, it is necessary to switch to the IAGA-approved standard methodology and update the $K9$ limit. The indices calculated on the basis of $Sq$ variations should be considered as only preliminary. Since the application of methods based on the $Sq$ variation leads to the same effect as the incorrect choice of the $K9$ limit, it is necessary to update this limit only using the digital $K$-index data calculated in accordance with one of the IAGA-approved methods. $K$-index data available in the World Data Center for Solar-Terrestrial Physics (http://www.wdcb.ru/stp/index.en.html) were calculated mainly from analog magnetogram data using the $Sq$ variation [Zabolotnaya, 2007] which is not suitable for this purpose.
$K$-index, introduced more than 80 years ago, is still a widely-used simple measure of geomagnetic activity. Modern data repositories for geomagnetism (such as the World Data Centers for Geomagnetism in Edinburgh or for Solar-Terrestrial Physics in Moscow) provide vast sets of data on $K$-index obtained within a long period of time. This makes $K$-index an indispensable instrument for retrospective analysis.
One of the pivotal aspects of creating an adequate $K$-index at geomagnetic observatories is the correct choice of the $K9$ limit value. This paper presents a feasible approach to correct determination of this value.
The $K9$ limit for most of the Russian observatories has not been reconsidered for several decades. To ensure the comparability of the $K$-index of Russian observatories with the international geomagnetic observational network, it is necessary to implement the IAGA standard methodology and update the value of the $K9$ limit. The indices calculated on the basis of $Sq$ variations should be considered only as preliminary.
Anisimov, S. V., E. M. Dmitriyev, et al. (2015) , Calculations of geomagnetic activity $K$-indices in real time, Heliogeophysical Research, 13, p. 62–72 (in Russian).
Bartels, J. (1938) , Potsdamer erdmagnetische Kennziffern, 1 Mitteilung, Zeitschrift für Geophysik, 14, p. 68–78 (in German).
Bartels, J. (1949) , The standardized index $Ks$ and the planetary index $Kp$, IATME Bulletin, 12b, p. 97–120.
Bartels, J. (1957) , The technique of scaling indices $K$ and $Q$ of geomagnetic activity, Geomagnetism: Annals of The International Geophysical Year, 4, p. 215–226, https://doi.org/10.1016/b978-1-4832-1304-0.50006-3.
Bartels, J., N. H. Heck, H. F. Johnston (1939) , The three-hour-range index measuring geomagnetic activity, Journal of Geophysical Research, 44, no. 4, p. 411–454, https://doi.org/10.1029/te044i004p00411.
Chulliat, A., S. Anisimov (2008) , The Borok INTERMAGNET magnetic observatory, Russian Journal of Earth Sciences, 10, no. 3, p. 1–7, https://doi.org/10.2205/2007es000238.
Coles, R., M. Menvielle (1991) , Some thoughts concerning new digital magnetic indices, Geophysical Transactions, 36, p. 303–312.
Hattingh, M., L. Loubser, D. Nagtegaal (1989) , Computer $K$-index estimation by a new linear-phase, robust, non-linear smoothing method, Geophysical Journal International, 99, no. 3, p. 533–547, https://doi.org/10.1111/j.1365-246x.1989.tb02038.x.
Love, J. J., K. J. Remick (2007) , Magnetic indices, Encyclopedia of Geomagnetism and Paleomagnetism, D. Gubbins and E. Herrero-Bervera (eds.), p. 509–512, Springer, Netherlands, https://doi.org/10.1007/978-1-4020-4423-6_178.
Mandrikova, O. V., S. E. Smirnov, I. S. Solov'ev (2012) , Method for determining the geomagnetic activity index based on wavelet packets, Geomagnetism and Aeronomy, 52, no. 1, p. 111–120, https://doi.org/10.1134/s0016793211060107.
Mayaud, P. N. (1967) , Atlas of indices $K$. Part 1, IAGA Bulletin No. 21, p. 112, IUGG Publication Office, Paris (http://isgi.unistra.fr/IAGABulletins/ IAGA_Bulletin_21text_Mayaud_1967.pdf).
Mayaud, P. N. (1980) , Derivation, Meaning, and Use of Geomagnetic Indices, Geophysical Monograph Vol. 22, AGU, Washington, DC, https://doi.org/10.1029/GM022 (Print ISBN: 9780875900223, Online ISBN: 9781118663837).
Menvielle, M. (1990) , About the derivation of geomagnetic indices from digital data, Proc. International Workshop on Observatory Data Acquisition and Processing, Geophysical Publications No. 15, Kauristie, K. et al. (eds.), p. 117–126, Finnish Meteorological Institute, Helsinki.
Menvielle, M. (1991) , Evaluation of algorithms for computer production of $K$ indices, Geophysical Transactions, 36, p. 313–320.
Menvielle, M., A. Berthelier (1991) , The $K$-derived planetary indices: Description and availability, Reviews of Geophysics, 29, no. 3, p. 415–432, https://doi.org/10.1029/91rg00994.
Menvielle, M., N. Papitashvili, et al. (1995) , Computer production of $K$-indices: review and comparison of methods, Geophysical Journal International, 123, no. 3, p. 866–886, https://doi.org/10.1111/j.1365-246x.1995.tb06895.x.
Nowoyski, K., T. Ernst, J. Jankowski (1991) , Adaptive smoothing method for computer derivation of $K$-indices, Geophysical Journal International, 104, no. 1, p. 85–93, https://doi.org/10.1111/j.1365-246X.1991.tb02495.x.
Sucksdorff, C., R. Pirjola, L. Häkkinen (1991) , Computer production of $K$-values based on linear elimination, Geophysical Transactions, 36, p. 333–345.
Wilson, L. R. (1987) , An evaluation of digitally derived $K$-indices, Journal of Geomagnetism and Geoelectricity, 39, no. 2, p. 97–109, https://doi.org/10.5636/jgg.39.97.
Zabolotnaya, N. A. (2007) , Indices of Geomagnetic Activity, LKI, Moscow (in Russian).
Received 7 May 2020; accepted 29 June 2020; published 23 November 2020.


Citation: Petrov Valery G., Roman I. Krasnoperov (2020), The aspects of
Copyright 2020 by the Geophysical Center RAS.