RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 20, ES5006, doi:10.2205/2020ES000705, 2020
Olga V. Pavlenko
Schmidt Institute of Physics of the Earth of the Russian Academy of Sciences, Moscow, Russia
Regional characteristics of radiation and propagation of seismic waves in the north-eastern Caucasus are estimated based on $\sim 40$ records of local earthquakes obtained by seismic station "Makhachkala" (MAK) (magnitudes $m_b \sim 3.0-5.7$, epicentral distances $r \sim 30-190$ km). Strong earthquakes with magnitudes $Mw \sim 7.5$ are probable there, and knowledge of characteristics of radiation and propagation of seismic waves is necessary for correct assessments of seismic hazard in the region. Previously, the quality function of the earth's crust and the upper mantle was estimated by the envelope method and by coda normalization method. Empirical methods and stochastic simulations were applied to estimate other parameters, such as, the stress drop ($\Delta \sigma \sim 50$ bars), the geometrical spreading (as a three-segment function $1/r$ for $r \sim 1-50$ km, 1/50 for $r \sim 50-150$ km and $1/\sqrt{r}$ for $r >150$ km), the duration of seismic motion depending on the hypocentral distance, kappa value ($\kappa \sim 0.08$ s), the amplification of seismic waves in the upper parts of the Earth's crust $A(f)$, and some others. The estimated characteristics of radiation and propagation of seismic waves show a good agreement between the simulations and observations and can be used for forecasting parameters of strong ground motion in future strong earthquakes in the region. Generally, the obtained characteristics of radiation and propagation of seismic waves are close to similar characteristics of the north-western Caucasus (Sochi and Anapa areas) and of central Japan.
To reduce damage from earthquakes, for design and construction of earthquake-resistant structures in seismic areas we should know parameters of strong ground motion during possible future earthquakes, such as, peak ground accelerations (PGAs), peak ground velocities and displacements, response spectra, intensities and durations of motion, predominant periods, etc. The parameters should be evaluated accounting for local site conditions. Complicated and expensive buildings and unique facilities are constructed now in seismic areas that require the assessment of ground motion parameters in future strong earthquakes with the highest possible accuracy.
Reliable methods for estimating the parameters of ground motion are based on records of local earthquakes. If a rather large number of earthquake records are accumulated in a region, we can derive ground motion prediction equations (GMPE) and obtain the required estimates from the GMPEs.
In Russia, we still do not have enough strong motion records from seismically active regions, exept Kuril-Kamchatka zone, mainly due to the large territory of the country. The Kuril-Kamchatka focal zone has been intensively studied last decades, and the seismic source and path characteristics, such as, the shapes of the source spectra, the frequency-dependent attenuation and the geometrical spreading are now well known [Abubakirov and Gusev, 1990]. The soil structure, soil response during strong ground motion, and local site effects are studied within the territory of Petropavlovsk-Kamchatsky city and adjacent areas [Pavlenko, 2013]. Considerable amounts of strong-motion records are available, and we can deduce GMPEs to predict parameters of ground motion in future strong earthquakes.
At the same time, some other areas of high seismicity in Russia, such as, the northern Caucasus, the Altai-Sayan region, the Baikal rift zone, Magadan region, Yakutia, Chukotka, Sakhalin still remain insufficiently studied, because they possess fewer strong motion records that do not allow the development of regional GMPEs.
As known, in regions where insufficient amounts of strong motion records are available, another approach is efficient: stochastic simulations are usually used instead of ground motion prediction equations [Halldorsson and Papageorgiou, 2005]. Regional characteristics of radiation and propagation of seismic waves are estimated based on the available records of local earthquakes and used as input parameters to stochastic simulations of acceleration time histories of possible future strong earthquakes [Boore, 2003]. Then ground motion parameters required for earthquake-resistant design and construction are estimated based on the simulated acceleration time histories. The approach was proposed by Japanese seismologists K. Aki and K. Irikura [1991]: "Since any ground motion parameters can be extracted from the acceleration time series, we shall compute the time series for a given source-receiver pair using the state-of-the-art method on the basis of our current knowledge on the earthquake source, propagation path and recording site condition".
Further accumulation of strong motion records in the region allows us to improve and refine the obtained estimates of the regional characteristics of radiation and propagation of seismic waves and increase the accuracy of forecasting parameters of ground motion in future strong earthquakes.
This approach is widely used in Russia for seismic hazard assessment in seismic areas. It was applied in Kuril-Kamchatka seismic zone [Pavlenko, 2013], in the northern Caucasus [Pavlenko, 2008, 2016a], in Buryatia [Pavlenko and Tubanov, 2017], in Altai-Sayan region [Emanov et al., 2020].
Characteristics of radiation and propagation of seismic waves in the northern Caucasus have been studied during last years [Pavlenko, 2008, 2009, 2016a, 2016b; Pavlenko and Pavlenko, 2016]. The northern Caucasus is an earthquake-prone region in Russia, where earthquakes with magnitudes $Mw \sim 7.0-7.5$ are possible. According to seismic zonation maps of Russian Federation, the area of potential earthquake sources with a maximum magnitude of 7.5 starts to the south of Makhachkala and goes through Derbent along the coast of the Caspian sea to the southeast.
This is a seismically active region, where strong earthquakes occurred in the past. A series of strong earthquakes occurred in the vicinity of the city of Shemakha ($\sim 300$ km to the south of Makhachkala) – so-called Shemakha earthquakes in 1667 ($M\sim 6.9$), 1669 ($M\sim 5.7$), 1671 ($M\sim 5.7$), 1828 ($M \sim 5.7$), 1859 ($M \sim 5.9$), 1872 ($M\sim 5.7$), and the strongest one – in 1902 ($M \sim 6.9$). The catastrophic Dagestan earthquake occurred in 1970 near Makhachkala, with a magnitude $Mw \sim 6.7$ and the hypocentral coordinates of 43° N and 47.06° E. The foreshock was recorded at 12:20, it had a magnitude $Mw\sim 5.7$, and the depth $h \sim 18$ km; the main shock occurred at 21:12 with a magnitude $Mw \sim 5.7$ and depth $h\sim 12$ km; then followed a series of powerful and numerous aftershocks. The epicenter was located at $\sim 30$ km from Makhachkala. The earthquake caused damage in the cities and villages of Dagestan, where more than 50% of the population lived. 31 people were killed, about 45 thousand people were left homeless [Arefiev et al., 2004].
During last decades, high-rise buildings and unique complicated constructions are built there, including facilities and the infrastructure for the 2014 winter Olympic Games in Sochi, which required responsible design solutions to ensure their seismic resistance. In papers [Pavlenko, 2008, 2016a], records of $\sim 60$ local earthquakes obtained by seismic stations "Sochi" (SOC) and "Anapa" (ANN) were used to estimate the frequency-dependent quality function of the crust and the upper mantle by coda-normalization method. The estimates were obtained $Q(f) \sim 55 f^{0.9}$ for Sochi area and $Q(f) \sim 90 f^{0.7}$ for Anapa area. The geometrical spreading was described by a three-segment function depending on the hypocentral distance $r$, as $1/r$ for $r \sim 1-50$ km, 1/50 for $r \sim 50-150$ km and $1/\sqrt{r}$ for $r >150$ km.
Based on records of $\sim 40$ earthquakes ($M_W > 3.9$) obtained by seismic station "Anapa" (ANN), Kromsky et al. [2018] estimated earthquake source parameters and the quality function in Anapa area by the methods of coda-wave analysis allowing the separation of source and path effects. For epicentral distances $r < 120$ km, the quality function can be described as $Q(f) \sim 90 f^{0.7}$, and for $r >120$ km as $Q(f) \sim 90 f^{1.0}$. No dependence was revealed between the shapes of the source spectra and the earthquake magnitudes in the magnitude range $M_W \sim 3.9 - 5.6$; it was also found that high-frequency radiation ($f > 4-5$ Hz) grows with the source depth $h$ down to $h\sim 60$ km (the maximal source depth of the studied earthquakes).
Pavlenko and Pavlenko [2016] estimated the quality function $Q(f)$ of the earth's crust and the upper mantle in the area of Kislovodsk city by coda normalization method. The geometrical spreading was described by a three-segment function of the hypocentral distance $r$, as $1/r$ for $r \sim 1-50$ km, 1/50 for $r \sim 50-150$ km and $1/\sqrt{r}$ for $r >150$ km. For this model of geometrical spreading, $Q(f)$ was estimated as $Q(f) \sim 85 f^{0.9}$ in the frequency range $f \sim 1 - 20$ Hz.
Kirsanov and Pavlenko [2019] estimated the quality function $Q(f)$ of the crust and the upper mantle in the north-eastern Caucasus based on records of $\sim 40$ local earthquakes obtained by seismic station "Makhachkala" (MAK). The quality function was estimated by the envelope method as $Q(f) \sim 95 f^{1.0}$ and by coda normalization method for frequencies up to $\sim 16$ Hz as $Q(f) \sim 135 f^{0.7}$, accounting for the geometrical spreading in the form $1/r$. Later, the calculations were repeated with the geometrical spreading function in the form $1/r$ for $r \sim 1-50$ km, 1/50 for $r \sim 50-150$ km and $1/\sqrt{r}$ for $r >150$ km, and the estimates $Q(f) \sim 100 f^{0.9}$ were obtained [Pavlenko, 2020]. Finally, $Q(f) \sim 100 f^{0.9}$ was taken as a joint estimate of the quality function in Makhachkala area.
Regional characteristics of radiation and propagation of seismic waves in the northern Caucasus in Sochi and Anapa areas were studied in [Pavlenko, 2008, 2016b]. Parameters defining the shapes of the source spectra, the amplification of seismic waves in the upper parts of the earth's crust, the attenuation of seismic waves at high frequencies (parameter kappa $\kappa$), and parameters defining the waveforms and durations of acceleration time histories were estimated by stochastic simulations. In the simulations, regional estimates of the quality function $Q(f)$ were used that were obtained earlier in [Pavlenko, 2008, 2016a].
Kharazova et al. [2016] interpret the estimated characteristics of radiation and propagation of seismic waves in the northern Caucasus in terms of the geologic and tectonic structure of the region. The estimates of the quality functions $Q(f) \sim 55 f^{0.9}$ (in Sochi area) and $Q(f) \sim 90 f^{0.7}$ (in Anapa area), the amplification of seismic waves in the upper parts of the earth's crust $A(f) \sim 1$, and the distribution of deviations of the simulated PGAs from the observed ones indicating local variations in ground motion parameters are analysed and discussed. For the analysis, all available information is involved about the tectonic and geologic deep structure of the northern Caucasus and the adjacent parts of the Black sea. The established differences in the quality functions at low frequencies in Sochi and Anapa areas can be explained by the tectonic dislocations and the geological environment in the areas. Local variations of characteristics of radiation and propagation of seismic waves can be associated with the features of the geological structure in the studied areas, such as, the faults, thrusts and crushing zones, inclined seismic boundaries, variations in the thickness and consolidation of the sedimentary cover, the structure and composition of the basement.
Thus during last years, the features of radiation and propagation of seismic waves in the northern Caucasus were studied, and the estimates of their characteristics were obtained.
In this paper, the studies of radiation and propagation of seismic waves in the northern Caucasus are continued. Records of local earthquakes obtained by seismic station "Makhachkala" (MAK) are simulated, and characteristics of radiation and propagation of seismic waves in the north-eastern Caucasus (in Makhachkala area) are estimated, such as, parameters defining the shapes of the source spectra and the stress drop, the amplification of seismic waves in the upper parts of the earth's crust, the attenuation of seismic waves at high frequencies described by kappa parameter, parameters defining the waveforms and duration of strong motion, and some others. The obtained estimates are discussed and compared with those obtained earlier for the north-western Caucasus (in Sochi and Anapa areas).
Characteristics of radiation and propagation of seismic waves are estimated by means of inversions. Records of local earthquakes are simulated by the stochastic method [Boore, 2003] and calibrated against the data recorded at MAK seismic station (42.987° N, 47.490° E).
A rather simple and effective stochastic approach is based on the observation-supported representations that acceleration time histories in the near-fault zones can be described as a band-limited Gaussian white noise. The frequency limits are defined by the boundary frequency $f_0$ and the highest frequency $f_{\max}$, which depends on the recording device or on the attenuation in the earth's crust [Hanks and McGuirre, 1981]. The simulated accelerograms adequately represent high-frequency components of seismic motion ($f > 0.1$ Hz), the most interesting for engineering seismology. By applying the stochastic approach, we can rather accurately predict parameters of strong ground motion based on records of weaker motion, so the method is widely used in seismic areas where few earthquake records are available [Boore, 2003].
The input data to stochastic simulations include parameters describing radiation (source effects), propagation (path effects) of seismic waves, and local site effects. The input parameters define the shapes of the source spectra, the stress drop, the geometrical spreading, the anelastic attenuation of seismic waves in the earth's crust and the upper mantle, parameters describing the duration of strong motion, the local amplification of seismic waves in the upper parts of the crust and their damping at high frequencies (parameter kappa $\kappa$), parameters defining the waveforms, and some others.
 |
| Figure 1 |
 |
| Table 1 |
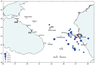
In this research, records of $\sim 40$ earthquakes obtained by seismic station "Makhachkala" (MAK) during the period of its digital registration (2005–2015) are simulated. The station was located in the central part of Makhachkala city, on the territory of Dagestan Scientific Center of Russian Academy of Sciences (in 2015 the station was destroyed). Table 1 presents the catalogue of the studied earthquakes, and Figure 1 shows the locations of the earthquake epicenters and seismic stations "Anapa" (ANN), "Sochi" (SOC), "Kislovodsk" (KIV) and "Makhachkala" (MAK). The coordinates and depths of the earthquake hypocenters (Table 1) are taken according to ISC (International Seismological Center) data, because they seem to be more accurate (better satisfy the observations, as preliminary calculations shown). The earthquake magnitudes $m_b$ are given in two versions, according to ISC and according to the Russian Geophysical Service (in brackets). As seen from the Table, the estimates by RGS are higher by $\sim 0.37$ units in the average, with the standard deviation of $\sim 0.35$ units (the only exclusion is the event of 31 July 2014), and the reason is not clear yet.
 |
| Figure 2 |
As seen from Table 1, the magnitudes and the hypocentral distances of the studied earthquakes are within the ranges $m_b \sim 3.0-5.7$ and $r_h \sim 29 -208$ km; the depths of the hypocenters vary from $\sim 5$ km to $\sim 83$ km (one earthquake is shallow: $h \sim 0.1$ km). The histograms showing the distributions of the studied earthquakes by the hypocentral distances $r_h$, source depths $h$, and magnitudes $m_b$ are presented in Figure 2. The histograms show us the predominance of seismic events with source depths $h \sim 5-25$ km and magnitudes $m_b \sim 3.6-4.8$ and no prevailing hypocentral distances (Figure 2).
In the simulations, the ground motions are calculated as deterministic functions with random phase spectra; the intensities and durations of motions being dependent on the magnitude of an earthquake and the epicentral distance. The sources are assumed to be point sources, because the earthquakes are rather weak (Table 1). For the calculations, the computer code SMSIM by D. Boore was used, supplemented by the author's computer code to account for ground response during strong motion at MAK site. The soil response was calculated according to the algorithm of nonlinear analysis by Joyner and Chen [1975]. The propagation of vertically incident shear waves in the horizontally layered sediments was calculated, and the soil behavior was described by normalized stress-strain relations similar to those obtained in laboratory experiments by Hardin and Drnevich [1972]. The soil profile at MAK site contains firm loams in surface layers (down to $\sim 14$ m, $S$-wave velocities $V_s \sim 650$ m/s), and dense firm mudstone below with $V_s$ increasing from $\sim 950$ m/s to $\sim 1000$ m/s at depths of $\sim 100$ m. Shear stresses in failure and densities in soil layers were estimated based on the composition of the soil, its depth, and saturation with water.
For earthquake recording, seismic station "Makhachkala" was equipped by the digital station SDAS v 2.4, which included a unit for signal acquisition, a timing system, systems for archiving and processing data, and magnetoelectric sensors SM-3KV (Russian production). The observed and simulated acceleration time histories and their spectra were compared, and input parameters to the stochastic simulation were selected, which give the best agreement between the observations and simulations in time and frequency domains. The agreement was estimated by the deviations of the PGAs, intensities and spectral amplitudes of the simulated accelerograms from the observed ones.
Partially input parameters to stochastic simulation such as, the quality function, geometrical spreading, and parameters describing the duration of seismic motion depending on the distance from the source, were estimated directly from the earthquake records.
Study of regional characteristics of radiation and propagation of seismic waves usually starts from the estimation of the quality function $Q(f)$, characterizing the absorption and scattering of seismic waves in the earth's crust and the upper mantle. As described above, we obtained $Q(f) \sim 100f^{0.9}$ for Makhachkala area, which generally agrees with the earlier obtained estimates of the quality functions in Anapa ($Q(f) \sim 90 f^{0.7}$), Sochi ($Q(f) \sim 55 f^{0.9}$), and Kislovodsk ($Q(f) \sim 85 f^{0.9}$) areas. Along with the geometrical spreading, $Q(f)$ describes the effects of propagation of seismic waves:
\begin{eqnarray*} P(R, f) = Z(R) \exp[- \pi fR /Q(f) v], \end{eqnarray*}where $v$ is the velocity of body $P$- or $S$-waves, and $Z(R)$ is the geometrical spreading.
As known, the geometrical spreading function is related to the structure of the earth's crust in the region. In a homogeneous elastic space, the amplitudes of seismic waves radiated by an isotropic point source are inversely proportional to the source – receiver distance $r$ [Aki and Richards, 1980]. The geometrical spreading in the form $\sim 1/r$ is observed in subduction zone in Kamchatka [Shumilina et al., 2000] and in Japan, where it is described by $\sim 1/r^n$, $n \sim 1 - 1.25$ [Petukhin et al., 2003]. Whereas, in regions with continental-type crust we usually observe a rapid decay of the amplitudes with distance at $r < 50-70$ km, and slower decay at distances $r > 120-150$ km, with no decay at the intermediate distances [Atkinson and Mereu, 1992; Boore, 2003]. The lack of the amplitude decay at $50-70$ km$ < r < 120-150$ km is attributed to intense post-critical reflections from the mid-lower crustal layers and Moho [Burger et al., 1987]. If a seismic source is located in the earth's crust at distances $r \sim 120-150$ km, we usually observe the superposition of surface waves with the geometrical spreading $Z(r) \sim r^{0.5}$ [Wang and Herrmann, 1980]. Thus, in regions with continental-type crust the geometrical spreading is usually described by a three-segment piecewise function, such as, $1/r$ for $r \sim 1$ to 50–70 km, 1/70–1/50 for $r \sim 50-70$ km to 120–150 km and $1/\sqrt{r}$ for $r > 120-150$ km [Boore, 2003].
In the northern Caucasus, the thickness of the crust is $\sim 44-48$ km [Natalenko, 2001], and therefore in Makhachkala area we can expect "typical" three-segment geometrical spreading described above. The geometrical spreading function of the type $1/r$ for $r \sim 1-50$ km, 1/50 for $r \sim 50-150$ km and $1/\sqrt{r}$ for $r >150$ km showed the minimum scattering during the estimation of the quality function $Q(f)$ in Makhachkala area by coda-normalization method.
 |
| Figure 3 |
According to [Chapman and Godbee, 2012], we can conclude about geometrical spreading in the region based on seismic observations, velocity structure of the earth's crust, and numerical simulation, if necessary. Figure 3a shows $S$-wave amplitudes normalized by coda $As/Ac$ corrected for lapse times (i.e., the ratios used for $Q(f)$ evaluation) depending on the hypocentral distance (the mixture of data is shown at different frequency bands and at two horizontal components). The normalized $S$-wave amplitudes were averaged within 15-km intervals of hypocentral distances (with central distances at 22.5 km, 37.5 km, 52.5 km, etc.). The obtained averages can be approximated by a three-segment piecewise function (Figure 3a.
As seen from the graph, the coda-normalized $S$-wave amplitudes decrease with distance rather quickly (because of the geometrical spreading combined with the inelastic attenuation) up to distances $r \sim 50$ km; then their decrease slows down at $\sim 50-150$ km and quickens again at $r >150$ km. Thus, the geometrical spreading function was taken in the form $1/r$ for $r \sim 1- 50$ km, 1/50 for $r \sim 50-150$ km and $1/\sqrt{r}$ for $r >150$ km, which seems reasonable and fits the observations.
Then local amplification of seismic waves [Boore and Joyner, 1997] at MAK station was evaluated based on the available information on the velocity structure in the upper parts of the earth's crust (down to $\sim 20-30$ km) obtained by seismic exploration and deep sounding. The amplification occurs during the propagation of seismic waves up to the surface as a result of the decrease of seismic wave velocities and densities in the upper layers.
Information on the deep structure of the earth's crust in various regions of Russia is provided in [Rosnedra, 2013]. The Rosnedra [2013] contains deep seismic cross-sections along the profiles of deep seismic sounding, carried out during the period of 1972-1995. The profile "Krasnodar–Emba" is the closest to Makhachkala city; it was elaborated within the project BATHOLITH-2_1989 [Rosnedra, 2013]. The profile crosses the western part of the Caucasian fold system, the Scythian plate, the Karpinsky elevation, it runs along the northern coast of the Caspian Sea and ends in the south-eastern part of the Caspian depression in Kazakhstan. The profile demonstrates a fairly uniform horizontally-layered structure of the earth's crust (down to $\sim 50$ km) in areas to the north of Makhachkala (from Elista to Akhtuba River). "The Map of the basement depths at platform areas of Russia" and "The Map of Moho depths at platform areas of Russia" [Natalenko, 2001] show similar basement depths (10-20 km) and similar Moho boundary depths (44–48 km) around Makhachkala and along the profile in the vicinities of Makhachkala city.
The profiling data together with the regional velocity models [Asmanov et al., 2010] were used to estimate the local amplification of seismic waves at MAK site. In the calculations, $S$-wave velocities and densities in the vicinities of the earthquake sources were taken depending on the depths of the sources (Table 1), according to the profiling data and the regional velocity models [Asmanov et al., 2010]. Rather low amplification coefficients were obtained for MAK site, $A(f) \cong 1.0-2.0$ at low frequencies $f \leq 0.3$ Hz, and these estimates were used for the stochastic simulations.
Important parameters to stochastic simulations are parameters defining the duration of seismic motion. The durations of the available local earthquake records D95 were estimated according to Boore and Thompson [2014], as the intervals of seismic motion between the time at which the cumulative integral of the squared acceleration (normalized to unity at the end of the record) reaches 5% and 95% of the maximum. The obtained estimates (averaged over 2 horizontal components) are presented in Table 1 and in Figure 3b. As seen from the figure, we can assume a break of the duration function at hypocentral distances of $\sim 50$ km. Based on $D_{95}$ values and their dependence on the hypocentral distance, the duration function was estimated as a two-segment function in the form $0.41 r$ for $r < 50$ km and $20.5 s + 0.15 r$ for $r > 50$ km; it was found matching the observations. Similar estimates of strong motion duration were obtained for Sochi and Anapa areas [Pavlenko, 2016b]. Rather long duration of strong motion in the Caucasus is evidently associated with the fractured structure of the Caucasian mountains, possessing large amounts of multidirectional faults.
 |
| Figure 4 |
 |
| Figure 5 |
 |
| Figure 6 |
 |
| Figure 7 |
The results of the simulations are presented in Figure 4, Figure 5, Figure 6, and Figure 7, where the observed records (NS- and EW-components) and the simulated horizontal components of the acceleration time histories are shown together with their spectra, in ascending order of the hypocentral distance.
At the first step, accereration time histories were generated for the earthquakes (1) possessing the smallest epicentral distances (to minimize the number of path parameters), (2) for which moment magnitudes $Mw$ were estimated. For the simulations, we need knowledge of moment magnitudes, but the relation between the magnitudes $m_b$ (known) and $M_w$ is not studied yet for this region.
For some of the studied earthquakes $Mw$ estimates are provided by the Geophysical Survey of Russia (Obninsk), based on the records of the Caucasian seismic network (seismic stations SOC, ANN, KIV, and MAK).
The strongest earthquakes with the estimated moment magnitudes $Mw$ are the earthquakes occurred at 16 April 2013 ($r_h \sim 70$ km, $Mw \sim 4.5-5.0$), 24 September 2011 ($r_h \sim 139$ km, $Mw \sim 4.3-4.4$), and 5 July 2012 ($r_h \sim 144$ km, $Mw \sim 4.5$). ISC also provides the estimates of moment magnitudes for some earthquakes listed in Table 1, however the hypocentral distances are higher, $\sim 160-170$ km. These earthquakes were also used for verification of the simulations.
Selecting input parameters for the simulations, I accounted for our previous experience in simulating records of local earthquakes in Sochi and Anapa areas, where close estimates of source and path parameters were obtained, which may be typical for the northern Caucasus [Pavlenko, 2016b]. The radiation model $\omega^{-2}$ was chosen as the most widespread in the world and satisfying the source spectra of the Caucasian earthquakes. The stress drop was estimated $\Delta \sigma \sim 50$ bar (the same as in Sochi and Anapa areas), based on the condition of compliance of spectral amplitudes of the observed and simulated records in the frequency range $f \sim 1 - 5$ Hz. The earthquake sources were specified as point sources.
Based on the records of earthquakes with small epicentral distances (Figure 4) and earthquakes with known moment magnitude $Mw$, parameters of seismic wave attenuation at high frequencies kappa $\kappa$ [Anderson and Hough, 1984] were selected by simulating the decay of the acceleration spectra at high frequencies. Kappa estimates $\kappa \sim 0.08$ s were obtained, showing a rather high attenuation at high frequencies in the studied region. Then other modeling parameters were estimated in the simulations.
Finally, records of other earthquakes were simulated based on the estimated source and path parameters. Figure 4, Figure 5, Figure 6, and Figure 7 shows individual simulated acceleration time histories and spectra of the simulated accelerograms averaged within the series of the simulated accelerograms. As seen from the figures, a fairly good agreement between the simulations and observations was obtained, both in time and frequency domains.
In the simulations it was assumed that source and path parameters described above remain the same for all the studied earthquakes (this is reasonable, because similar source and path characteristics were found in adjacent Sochi and Anapa areas). The moment magnitudes $Mw$ were estimated based on $m_b$ (Table 1) according to average world regularities [Kanamori, 1993], and then slightly changed, if necessary, to better fit the observations. The obtained $Mw$ estimates can be considered as approximations to the moment magnitudes for the studied earthquakes.
Starting from the hypocentral distances $r_h \sim 160$ km, the quality function $Q(f)$ was corrected. For distances $r_h \sim 150 -209$ km, $Q(f)$ estimations by coda normalization method gave us the quality function in the form $Q(f) \sim 150f^{ 0.6}$, reflecting the decrease of attenuation of seismic waves at lower frequencies in deeper and denser layers. A similar result, i.e., increase of $Q_0$ and decrease of n with distance, was obtained for the northern Finland [Pavlenko and Kozlovskaya, 2018].
 |
| Table 2 |
The estimated parameters of radiation and propagation of seismic waves in Makhachkala area are shown in Table 2. The results of this research allow us to compare the obtained estimates of the parameters of radiation and propagation of seismic waves in the north-western (Sochi, Anapa) and north-eastern (Makhachkala) parts of the Caucasus. The stress-drop, source spectra (model $\omega^{-2}$), and parameters describing strong-motion duration are very similar, whereas, other parameters are different, such as, the quality function $Q(f)$, the local amplification $A(f)$, and kappa value $\kappa$. The obtained stress drop estimates $\Delta \sigma \sim 50$ bar combined with a low amplification of seismic waves in the earth's crust $A(f)$ indicate rather low levels of seismic motion intensity in the studied region.
In the whole, the obtained parameters of radiation and propagation of seismic waves in the north Caucasus resemble similar source and path characteristics of crustal earthquakes in central Japan, and the waveforms of the acceleration time histories also look similar in these two regions [Pavlenko, 2011].
Thus, characteristics of radiation and propagation of seismic waves for the north-eastern Caucasus are obtained, which can be used for prediction parameters of ground motion in future strong earthquakes in the region.
In the simulations, the estimates of frequency-dependent quality function $Q(f)$ were used in the form $Q(f) \sim 100 f^{0.9}$ for hypocentral distances $r_h <160$ km and $Q(f) \sim 150 f^{0.6}$ for $r_h >160$ km, and the geometrical spreading described by a three-segment function $1/r$ for $r < 50$ km, 1/50 for $50 \leq r < 150$ km and $1/r^{0.5}$ for $r > 150$ km. The amplification of seismic waves in the earth's crust was described by $A(f) \cong 1.0-2.0$ at $f \leq 0.3$ Hz, the stress drop by $\Delta \sigma \sim 50$ bar, and parameter kappa $\kappa \sim 0.08$ s.
In general, the estimated parameters of radiation and propagation of seismic waves are rather close in the western and eastern parts of the northern Caucasus and resembleing similar parameters for crustal seismicity in central Japan.
Accounting for the large territory of Russia, we may expect that characteristics of radiation and propagation of seismic waves in different seismic regions can vary greatly, leading to substantial differences in the acceleration time histories. Pavlenko [2011] has shown that, for a fixed magnitude (for example, $Mw \sim 5.4$) and an epicenter distance (for example, $r \sim 65$ km), the PGAs generated by a subduction-type earthquake in Kamchatka can be $\sim 10-15$ times higher than the PGAs generated by a crustal-type earthquake in the northern Caucasus. At the same time, the duration of strong motion during a Caucasian earthquake significantly exceeds the duration of strong motion during the earthquake in Kamchatka, so that the intensities of the two events are comparable.
So wide scattering of peak accelerations and durations of strong motion does not allow us to apply simple relations between PGAs and seismic intensities in Russia, the same for all seismic regions in the whole Russian territory. It is reasonable to draw seismic zonation maps in units of seismic intensity, instead of PGAs, as done in Japan, where similar differences in ground motion parameters occur during subduction-type and crustal-type earthquakes. In such cases, mapping of peak ground accelerations is problematic, and an urgent priority for Russian seismologists is a detailed study of the features of seismic wave radiation and propagation in various seismic regions.
Abubakirov, I. R., A. A. Gusev (1990) , Estimation of scattering properties of lithosphere of Kamchatka based on Monte-Carlo simulation of record envelope of a near earthquake, Phys. Earth Planet. Inter., 64, p. 52–67, https://doi.org/10.1016/0031-9201(90)90005-I.
Aki, K., K. Irikura (1991) , Characterization and mapping of earthquake shaking for seismic zonation, Proc. 4th Int Conf on Seismic Zonation, 1, p. 61–110, EERI, Stanford, California.
Aki, K., P. G. Richards (1980) , Quantitative Seismology. Theory and Methods, Freeman, San Francisco.
Anderson, J. G., S. E. Hough (1984) , A model for the shape of the Fourier amplitude spectrum of acceleration at high frequencies, Bull. Seism. Soc. Am., 74, p. 1969–1993.
Arefiev, S. S., E. I. Stasyuk, L. Rivera (2004) , The source model of the Dagestan earthquake of 1970, Izvestiya, Phys. Solid Earth, 2, p. 15–27.
Asmanov, O. A., A. R. Abdullaeva, et al. (2010) , The hodograph of seismic waves on the territory of Dagestan, Proc. Geol. Inst. Dagestan Sci. Cent., 56, p. 19–21.
Atkinson, G. M., R. Mereu (1992) , The shape of ground motion attenuation curves in southeastern Canada, Bull. Seism. Soc. Am., 82, p. 2014–2031.
Boore, D. M. (2003) , Simulation of Ground Motion Using the Stochastic Method, Pure Appl. Geoph., 160, p. 635–676, https://doi.org/10.1007/PL00012553.
Boore, D. M., W. B. Joyner (1997) , Site amplifications for Generic Rock Sites, Bull. Seism. Soc. Am., 87, p. 327–341.
Boore, D. M., E. M. Thompson (2014) , Path Durations for Use in the Stochastic-Method Simulation of Ground Motions, Bull. Seism. Soc. Am., 104, no. 5, p. 2541–2552, https://doi.org/10.1785/0120140058.
Burger, R. W., P. G. Sommerville, et al. (1987) , The effect of crustal structure on strong ground motion attenuation relations in eastern North America, Bull. Seism. Soc. Am., 77, p. 420–439.
Chapman, M. S., R. W. Godbee (2012) , Modeling Geometrical Spreading and the Relative Amplitudes of Vertical and Horizontal High-Frequency Ground Motions in Eastern North America, Bull. Seism. Soc. Am., https://doi.org/10.1785/0120110081.
Emanov, A. F., A. A. Emanov, O. V. Pavlenko, et al. (2020) , Kolyvan Earthquake of 09.01.2019 with magnitude $ML= 4.3$ and the features of induced seismicity in the Gorlovka coal basin, Probl. Eng. Seism., 3, p. 52–75.
Halldorsson, B., A. S. Papageorgiou (2005) , Calibration of the Specific Barrier Model to Earthquakes of Different Tectonic Regions, Bull. Seism. Soc. Am., 95, no. 4, p. 1276–1300, https://doi.org/10.1785/0120040157.
Hanks, T. C., R. K. McGuire (1981) , The character of high frequency strong ground motion, Bull. Seism. Soc. Am., 71, p. 2071–2095.
Hardin, B. O., V. P. Drnevich (1972) , Shear modulus and damping in soils: design equations and curves, Proc. Am. Soc. Civil Eng., J. Soil Mech. Found Div., 98, p. 667–692.
Joyner, W. B., T. F. Chen (1975) , Calculation of nonlinear ground response in earthquakes, Bull. Seism. Soc. Am., 65, p. 1315–1336.
Kanamori, H. (1993) , Magnitude scale and quantification of earthquakes, Quantification of Earthquakes Tectonophysics, Duda S. J., Aki K. (eds.), p. 185–199, https://doi.org/10.1016/0040-1951(83)90273-1.
Kharazova, Yu. V., O. V. Pavlenko, K. A. Dudinskii (2016) , The Correlation between the Characteristics of Seismic Wave Propagation in Western Caucasus and the Geological–Tectonic Features of the Region, Izvestiya, Phys. Solid Earth, 3, p. 399–412, https://doi.org/10.1134/S1069351316030046.
Kirsanov, V. I., O. V. Pavlenko (2019) , Assessment of quality factor of the crust and the upper mantle in the North-Eastern Caucasus based on the records of seismic station "Makhachkala", Probl. Eng. Seism., 2, p. 60–73.
Kromsky, S. D., O. V. Pavlenko, I. P. Gabsatarova (2018) , Manifestations of the peculiarities of radiation and propagation of seismic waves in the North Caucasus in Coda waves of regional earthquakes, Izvestiya, Phys. Solid Earth, 3, p. 33–44.
Natalenko, A. E. Ed. (2001) , The Structure of the crust and the upper mantle of Russian territory in maps and charts, Prospect and Protect of Mineral Resources, no. 2, p. 36 (in Russian).
Pavlenko, O. V. (2008) , Characteristics of seismic wave attenuation in the crust and upper mantle of the Northern Caucasus, Izvestiya, Phys. Solid Earth, 6, p. 487–494, https://doi.org/10.1134/S1069351308060049.
Pavlenko, O. V. (2009) , The study of the radiation characteristics and propagation of seismic waves in the North Caucasus by modeling the accelerograms of the recorded earthquakes, Izvestiya, Phys. Solid Earth, 10, p. 874–884, https://doi.org/10.1134/S106935130910005X.
Pavlenko, O. V. (2011) , Regional differences in the characteristics of seismic wave emission and propagation in Kamchatka and the Northern Caucasus, Doklady Earth Sciences, 438, no. 2, p. 846–852, https://doi.org/10.1134/S1028334X11060225.
Pavlenko, O. V. (2013) , Simulation of Ground Motion from Strong Earthquakes of Kamchatka Region (1992–1993) at Rock and Soil Sites, Pure Appl. Geoph., 170, no. 4, p. 571–595, https://doi.org/10.1007/s00024-012-0529-x.
Pavlenko, O. V. (2016a) , The Q-Factor Estimates for the Crust and Upper Mantle in the Vicinity of Sochi and Anapa (North Caucasus), Izvestiya, Phys. Solid Earth, 3, p. 353–363, https://doi.org/10.1134/S1069351316030101.
Pavlenko, O. V. (2016b) , Characteristics of radiation and propagation of seismic waves in the Northern Caucasus, estimated based on records of seismic stations "Sochi" and "Anapa", Probl. Eng. Seism., 1, p. 49–61.
Pavlenko, O. V. (2020) , Seismic wave absorption in the Eastern part of the North Caucasus Estimated from records of seismic station "Makhachkala", Izvestiya, Phys. Solid Earth, 1, p. 16–34.
Pavlenko, V. A., O. V. Pavlenko (2016) , The Seismic Wave Absorption in the Crust and Upper Mantle in the Vicinity of the Kislovodsk Seismic Station, Izvestiya, Phys. Solid Earth, 4, p. 492–502, https://doi.org/10.1134/S1069351316030113.
Pavlenko, O. V., Ts. A. Tubanov (2017) , Characteristics of Radiation and Propagation of Seismic Waves in the Baikal Rift Zone Estimated by Simulations of Acceleration Time Histories of the Recorded Earthquakes, Izvestiya, Phys. Solid Earth, 1, p. 18–31, https://doi.org/10.1134/S1069351317010116.
Pavlenko, O., E. Kozlovskaya (2018) , Characteristics of radiation and propagation of seismic waves in the Northern Finland estimated based on records of local earthquakes, Pure Appl. Geoph., 12, p. 4197–4223, https://doi.org/10.1007/s00024-018-1919-5.
Petukhin, A., K. Irikura, et al. (2003) , Estimation of Q-values in the Seismogenic and Aseismic Layers in the Kinki Region, Japan, by Elimination of Geometrical Spreading Effect Using Ray Approximation, Bull. Seism. Soc. Am., 93, p. 1498–1515, https://doi.org/10.1785/0120020205.
Rosnedra, (2013) , Deep seismic sections on the profiles of Deep Seismic Sounding GSS, elaborated in 1972–1995, Basic geological-geophysical profiles of Russia, p. electronic edition, Rosnedra, VSEGEI, Moscow.
Shumilina, L. S., A. A. Gusev, V. M. Pavlov (2000) , An improved technique for determination of seismic hazard, J. Earthq. Pred. Res., 8, p. 104–110.
Wang, C. Y., B. B. Herrmann (1980) , A numerical study of P-, SV-, and SH-wave generation in a plane layered medium, Bull. Seism. Soc. Am., 70, p. 1015–1036.
Received 4 February 2020; accepted 10 March 2020; published 17 September 2020.


Citation: Pavlenko Olga V. (2020), Regional characteristics of radiation and propagation of seismic waves in the North-Eastern Caucasus, Russ. J. Earth Sci., 20, ES5006, doi:10.2205/2020ES000705.
Copyright 2020 by the Geophysical Center RAS.