RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 20, ES2002, doi:10.2205/2020ES000694, 2020
Aleksandr M. Fedorov1,2, Tatyana V. Belonenko1
1Saint Petersburg State University, Saint Petersburg, Russia
2Scientific foundation "Nansen International Environmental and Remote Sensing Centre", Saint Petersburg, Russia
We explore the interaction of mesoscale eddies in the Lofoten Basin of the Norwegian Sea using the GLORYS 12v1 eddy-resolving reanalysis. The Lofoten Basin is the area of the intensive ocean-atmosphere interactions and many mesoscale eddies are formed due to instabilities of the branches of the Norwegian Current. We describe the spatial distribution of kinetic energy, relative vorticity, and Okubo-Weiss parameter during the eddy interaction. Using the approach of turbulent theory, we study the exchange of related eddy kinetic energy ($KmKe$) and show a strong dependence from a width of window averaging. The $KmKe$ fluxes describe features of interactions between parts of eddies and indicate a difference in the stability of the parts. The most stable parts have positive values of $KmKe$. They can transfer energy to the less stable parts. In other words, the positive values of $KmKe$ mean transport of kinetic energy from the main fluxes to turbulent pulsations. We demonstrate that the field of relative vorticity of one anticyclonic eddy merging with another one consists of three parts with alternating signs of $KmKe$. The parts look like two concentric rings surrounding the central part of the eddy. The sign of each part corresponds to gain or loss of kinetic energy. We detect the positive values of $KmKe$ for both the external ring and the central part of the eddy. For the middle ring of the eddy, $KmKe$ is negative. This demonstrates the tendency to the stability of the structure as the result of the merging. And vice versa, positive values of $KmKe$ break the eddy into two parts when splitting.
The Lofoten Basin (LB) is famous for strong eddy dynamics and the positive anomaly of heat and salt. This basin of the Norwegian Sea is the topographically isolated structure and is bordered on the east by the Scandinavian peninsula, the V{ring Plateau on the south, the Helgeland ridge on the south-west and the Mohn ridge on the north-west. The main source of heat and salt is the Norwegian current, which has subtropical Atlantic origin being a part of the North Atlantic current, in the LB it splits into two separate flows: the Norwegian Atlantic frontal current (NAFC) and the Norwegian Atlantic slope current (NASC). Relatively fresh and cold waters are transported by the Norwegian coastal current (NCC). Based on the facts above, it may be concluded that water exchange between the Lofoten Basin and the Arctic Ocean is completely absent in the surface layers [Blindheim and {sterhus, 2013] and can appear in intermediate and deep layers only. Thermohaline structure and topographical features form particular conditions for vortex generation in the LB.
 |
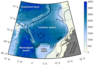
| Figure 1 |
The unique phenomenon of the LB is the quasi-permanent Lofoten Vortex (LV). The quasi-permanent LV is located in the flat deepest part of the basin (see the black dotted ring in Figure 1), where the depth reaches 3250 meters. There are several points of view nowadays on the nature of its existence. Firstly, mesoscale eddies splitting from the NASC under the effect of topography [Isachsen, 2011, 2015] drift through the LB and transfer warm and salty water to the central part of the basin [Köhl, 2007; Volkov et al., 2015]. These waters can be transformed during the splitting and merging of vortices on the way to the LV. Secondly, intensive winter mixing leads to regeneration of the intermediate waters in the area of the most frequent position of the LV [Bloshkina and Ivanov, 2016; Bashmachnikov et al., 2017b]. The mixed layer depth reaches over 1000 meters in the vortex core [Alexeev et al., 2016; Fedorov et al., 2019; S{iland et al., 2016].
The LB consisting of warm waters in comparison to the Greenland and Barents Seas [Volkov et al., 2013] is the area of the intensive heat release to the atmosphere in the thermodynamic system of the Atlantic Meridional Overturning Circulation locally, and in general, the LB is a part of the Great Ocean Conveyor Belt [Broeker, 1991; Lozier, 2010]. Probably, mesoscale eddy drift can be one of the main processes which affect the accumulation of the heat inside the basin. Investigation of mesoscale eddy interactions is significant in the context of water formation in the area and it can be a key to understanding how the vortex splitting and merging can modify thermodynamic parameters of transporting waters [Carton, 2001].
Being a complex deterministic nonlinear physical event on the one hand and purely random large-scale turbulent system, on the other hand, the vortex can be described in terms of turbulent viscosity [Carton, 2001; Dong et al., 2007]. Deformations of its cores, merging, splitting, shape stretching, or dissipations take place, while vortices interact. It leads to transformations of kinematic and geometric parameters during the process of interaction, and eddy kinetic energy redistributes between interacting eddies. Features of kinetic energy fluctuations make visible baroclinic instability manifestations in vortex-vortex interactions. Such purpose needs the usage of Reynolds averaging which implies a division of the incoming signal on two components: main flow and pulsations, meanwhile turbulence can be characterized by both negative and positive viscosity [Starr, 1966]. Such an approach assumes the consideration of larger vortex structures as a background flow on the mesoscales while there is not intensive current in the field of interaction. In this way, small mesoscale eddies around the bigger one are influenced by the eddy currents of the neighboring bigger vortex which is background flow of vortex origin. If turbulence is energized by average movements only through the instability of big gradients of the mean velocities and turbulent eddies are energized the same way, then turbulent viscosity will be positive, and energy and momentum will be transported from the areas with high velocities to the low-speed areas. The existence of the positive turbulent viscosity leads to the dissipation of the kinetic energy in the main flow moreover dispersed energy goes to the pulsations. On the contrary negative turbulent viscosity points to energy conservation of the background flow, but herewith pulsations decrease [Starr, 1966]. The objective of the division velocity field on the components (pulsations and background) may be ambiguous, in that case, the compromise is to find appropriate averaging window width depending on the scale of the process under consideration. Thus, the main purpose of the study is to analyze kinematic parameters of the horizontal mesoscale eddies interacting in the LB and to assess the $KmKe$ redistributed between individual vortex structures.
GLORYS 12v1 is the main source of data for the current research. The dataset constitutes a daily eddy-resolving reanalysis of the global ocean that is available at Copernicus Marine Environment Monitoring Service (CMEMS) [http://marine.copernicus.eu]. Temperature, salinity, current velocities, sea surface height, and other parameters are distributed on 1/12° ($8 \times 8$ km in average) orthogonal grid at 50 depth levels for 1993–2016.
The use of this dataset for the Lofoten Basin is efficient due to the existence of regular contact measurements (e.g. over 5000 Argo profiles for 2005–2016 (see Figure 3 in [Fedorov et al., 2019]. Chen et al. [2019] have compared GLORYS 12v1 and ARMOR3D (tree-dimensional reconstruction of the oceanic conditions based on a statistical analysis of contact and remote sensing measurements) and have confirmed the fact of good compliance of these datasets.
Ocean model for GLORYS is NEMO LIM2 EVP with ERA-interim forcing: the coupled model includes dynamics of oceanic circulation and ice. Sea surface temperature, sea ice concentration, absolute dynamic topography satellite data co-assimilates with in-situ contact measurements (temperature and salinity vertical soundings) from CMEMS CORAv4.1. Data assimilation determines the vitality of usage GLORYS 12 v1 for the current paper.
Spatial distributions of the typical parameters and their variability calculated using GLORYS dataset are analyzed in the context of vortex-vortex interactions.
Components of velocity on the surface were used for relative vorticity $\zeta$ and Okubo-Weiss $W$ (1) parameter [Okubo, 1970; Weiss, 1991] calculations. The sign of relative vorticity allows us to recognize the direction of the fluid rotation: negative values – anticyclonic, positive – cyclonic rotation. Okubo-Weiss parameter evaluates the proportion of shearing and vortex components of motion, therefore negative values of $W$ are a referent in case of vortex component prevalence over shearing:
\begin{equation} \tag*{(1)} W=s_n^2 + s_s^2 - \zeta^2, \; [\mathrm{s}^{-2}], \end{equation}here
\begin{eqnarray*} \zeta = \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y} \; - \mbox{relative vorticity}, [\mathrm{s}^{-1}], \end{eqnarray*}\begin{eqnarray*} s_n = \frac{\partial u}{\partial x} - \frac{\partial v}{\partial y}\: - \mbox{normal component} \mbox{of strain}, [\mathrm{s}^{-1}], \end{eqnarray*}
\begin{eqnarray*} s_s = \frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}\: - \mbox{shear component} \mbox{of strain}, [\mathrm{s}^{-1}], \end{eqnarray*}
here $u$ and $v$ – zonal and meridional components of the current velocity, the abscissa is oriented eastward and ordinate – northward. The location of the vortex core is characterized by negative values of $W$ only [Isern-Fontanet et al., 2003; Kurian et al., 2011], at the same time, nonzero values of the relative vorticity are typical as for vortices as for shearing currents.
Kinetic energy $KE = 0.5 \times \rho (u^2 + v^2)$ [J], here $\rho$ – average density ($\rho =1027$ [kg/m$^3$]), estimated on the surface.
Conversion of mean kinetic energy to eddy kinetic energy ($KmKe$) is estimated using the equation:
\begin{eqnarray*} KmKe = - \Bigl ( \overline{u' \times u'} \times \frac{\partial \bar{u}}{\partial x} + \overline{u' \times v'} \times v' \frac{\partial \bar{u}}{\partial y} + \end{eqnarray*}\begin{equation} \tag*{(2)} \overline{u' \times v'} \times \frac{\partial \bar{v}}{\partial x} + \overline{v' \times v'} \times \frac{\partial \bar{v}}{\partial y} \Bigr ), \; [\mathrm{m^2 s}^{-2}], \end{equation}
here $\bar{u}$ and $\bar{v}$ – obtained by Reynolds averaging (for period $T$) zonal and meridional components of velocity, $u' = u - \bar{u}$ and $v' = v - \bar{v}$ – zonal and meridional pulsations of velocities. When the $KmKe$ is positive it implicates baroclinic instability leading to an energy transfer from the background to pulsations.
Reynolds terminology requires division of the velocity field on the background and pulsation flows in the context of the mesoscale eddies interaction. When the vortex interacts with intensive jet stream averaging window width is more than a lifetime of the vortex and much more than the period of its generation as a consequence of baroclinic instability. At the same time, the velocities of the background flow correspond well to the velocities of the jet stream localized in a particular area. If considered mesoscale vortex is free from the influence of the jet stream and velocity around the vortex is lower than velocity in this vortex the width of averaging should be changed to appropriate value in conditions of constant displacement of location and lifetime of the each vortex. When a period $T$ is equal to several days, then background velocities include orbital velocities of the vortex hence pulsations will be understated. In the opposite case, when the width of $T$ is 3 months, for example, background flow almost disappears like in the central part of the LB (Figure 1).
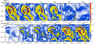 |
| Figure 2 |
Several situations of the vortex interaction are considered in the area bordered 69°–71° N, 9°–13° E in the LB. A series of experiments are carried out for various averaging window widths: $T= 3$, 7, 13, 15, 30, 60, 90 days. Figure 2 demonstrates background and pulsation distributions of velocities depending on the window width of Reynolds averaging. While the window width is 3 days the background vortex appears clearly as a large anticyclone, but pulsations are not significant. Further, the background currents are represented by the same large anticyclone and pulsations are manifesting as cyclones of lower scales for $T=7$ days. Noticeable that flux from background redistributes to pulsations with increasing $T$. The background currents almost disappear with the window of 90 days, yet the analyzed anticyclone is visible in the distribution of pulsations.
The analysis of a sequence of physical distributions illustrates that the interaction of vortices usually occurs rapidly enough in a few days. Based on that appropriate $T$ should be selected for each situation according to the sizes of the interacting structures. Furthermore, the lifetime of each structure is different and the long-living structure is more stable. Therefore, in frames of the current method more stable and long-living vortex can be considered as background flow relative to other less stable vortex structures. $KmKe$ in equation (2) reveals redistribution of energy between structures of different lifetime if the averaging window width is relatively small. Positive values correspond energy transfer from more to less stable vortex structures, herewith orbital velocities of more stable eddies represent background velocities within the framework of the proposed approach.
 |
| Figure 3 |
Figure 3 demonstrates the interaction of two anticyclones on the eastern slope of the Lofoten Basin according to sea level anomalies (SLA), relative vorticity and Okubo-Weiss parameter ($W$) spatial distributions. Based on SLA distribution it can be seen how two anticyclones move towards each other forming an eight-like structure, in the field of other parameters variety of several features are observed, so the processes of interaction of these two vortices are more complicated then appears.
At the first moment (1993.12.31) relative vorticity and $W$ spatial distributions permit the detection of the northern (70.2° N; 10.8° E) and the southern (69.2° N; 12.0° E) eddy structures. They are Northern and Southern anticyclones. Subsequently, at a moment (1994.01.05), substantial core deformation of the Southern anticyclone occurs resulting in the anticyclonic filament elongating northward. The filament is carried away by the flow propagating northward and afterward (1994.01.08) is engaged in rotating movement around a northern anticyclone. Then, at a moment (1994.01.11), we already observe two vortices on the latitude 70° N: transformed northern anticyclone and smaller cyclone. At a moment (1994.01.08), the cyclone located on the 69.5°–69.7° N; 10.0°–10.5° E cut the Southern Vortex on two parts, one of which merge later (1994.01.11) with the northern eddy, then the northern anticyclone increases in size. We can see that the Northern Vortex is more stable than the Southern one. The core of the first eddy is more stable during the period under consideration in comparison to the core of the second eddy, and this is manifested in the fields of relative vorticity and $W$ spatial distributions, at the same time the Southern Vortex decays on filaments (see the spatial distribution of $W$ at a moment 1994.01.11). At a moment (1994.01.11), we can see an only partial merger of two anticyclones (filament and the Northern Vortex) during which slight convergence of two cores and sea level alignment (an increase of SLA) occurs in the area between vortices (Figure 3). Nonetheless, a full merging of two corotated vortices is not completed, which is well seen on the relative vorticity and especially $W$ spatial distributions. Two described vortices are located quite close to each other so that the distance between them is much less than 3.3 of the radius of its cores what is so-called the critical value [Carton, 2001; Zhmur, 2011]. However, the full merging does not occur.
What prevented the full merging of these vortices? The reason may be as follows. There are shear currents in the periphery of the considered vortices (see vorticity and $W$ distributions in Figure 3). At the same time, there is a set of small cyclones, which are indicated by red color in the relative vorticity. Negative values of $W$ contribute to the detection of the cyclones. A purple color in Figure 3 indicates the location of the vortex structures. The effect of these cyclones on the interaction is understandable since the cyclones are induced by the anticyclones under consideration. An increase in the relative vorticity leads to the stronger bending of isopycnals in the stratified conditions. As a result, the relative vorticity of opposite sign increases on the periphery of the anticyclone to keep the balance of the potential vorticity [Belonenko et al., 2017; Bashmachnikov et al., 2017a, 2018; Carton, 2001]. Exactly, these cyclonic structures placing in the frontier zone between anticyclones prevented the full merging of the described vortices.
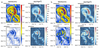 |
| Figure 4 |
Transformation of vortices usually occurs very rapidly, for this reason, we use short period $T$ for the Reynolds averaging. Figure 4a demonstrates the background velocities up to 0.70 m/s that characterize the vortex since the pulsations have velocities less 0.15 m/s. Note the kinetic energy of background flow 20 times exceeds the same for pulsations. If we increase period $T$ to 7 days (Figure 4b), the pattern of currents remains the same, yet the values of velocity components change significantly. The background velocities decrease since pulsations arise proportionally. The values of the pulsation velocities are doubled, and the kinetic energy values increase 4 times. Figure 4 indicates that maxima of the background flow velocities, pulsations, and kinetic energy are concentrated predominantly on the periphery of eddies.
 |
| Figure 5 |
Note the external ring-shaped periphery of anticyclone features by positive values of $KmKe$ flux. A similar pattern takes place in the middle of the eddy where values of $KmKe$ reach $10^{-8}$ m$^2$ s$^{-2}$ while a ring between these areas includes negative $KmKe$ values (Figure 5a). As a comparison, we can note that if the period $T$ is equal to 7 days, $KmKe$ flux distributes almost the same way, although there are some differences in the configuration of the kinetic energy flow regions, as well as the values of energy flows. Figure 5b displays the negligible changes in the shape of the areas with positive and negative values as well as slight variations in the values of the velocities. The facts given mean the turbulence is energized in the external ring of the vortex and its core (a central part of the eddy), at the same time the negative ring placed between them indicates a tendency to stability.
Summing up, we can conclude based on the described example: the energy fluxes directed from the background to the pulsations are characteristic for the periphery and the core of the anticyclonic vortex while the area between them has the opposite way of energy exchange. Following Victor Starr's terminology, the influence of positive viscosity lies in prevention from relative motions of the liquid, while the effect of negative viscosity supports the velocity difference and its growths [Starr, 1966].
 |
| Figure 6 |
Analyzed vortices consist of the vortex core and waters induced by this vortex. The core of the vortex rotates around a vertical axis similar to the rotation of the solid body [Zhmur, 2011]. Orbital velocities in the center of the core equal to zero. They increase moving away from the eddy rotation axis, and they become equal to zero on the border of the waters involved in rotating. This is the boundary of the eddy [Bashmachnikov et al., 2018]. That means that the sign of vorticity inside and outside (induced waters) the core has to be different. Figure 3 illustrates a series of spatial distributions and it shows the way how induced waters rotate with the vortex core in the same direction (clockwise), which is well seen in spatial distributions of relative vorticity. Figure 6 shows that the main axis of the Northern Vortex rotates clockwise for $90\mbox{°}$ with an angular velocity equal to $30\mbox{°}$ per day (0.52 radian day$^{-1}$) for 3 days (1994.01.07–1994.01.09) while the rotation of the shear currents is rather insignificant. A comparison of the distributions in Figure 5 and Figure 6 reveals the negative values $KmKe$ flux to be typical for the areas with the highest gradient of the relative vorticity.
 |
| Figure 7 |
 |
| Figure 8 |
Figure 7a demonstrates a spatial distribution of SLA at a moment (1994.01.13). It reveals an eddy structure with two cores but so far with an inseparable rotation. Figure 7b displays for cores indivisible anticyclonic circulation. An increase of the current velocity on the eastern periphery of the vortex leads eventually to a generation of a filament with vorticity of an opposite sign. It is visible on the charts at a moment (1994.01.16). This filament manifesting in the fields of $W$ and relative vorticity crosses the vortex under consideration on two parts. Subsequently, the increase of the velocity causes the splitting of the vortex onto two independent anticyclonic eddy structures (1994.01.19). Intensification of the velocity in the eastern periphery of the vortex appears in both the background and the pulsating currents with a period of averaging $T = 7$ days. The energy transformation in this type of vortex transformation is shown in Figure 8. The $KmKe$ distribution in Figure 8b, in this case, forms a very complicated structure, however, positive values relate to the areas where the vortex splitting occurs. This fact is evidence the background flow exactly is responsible for the splitting of this vortex, but not pulsations. An increase of the background flow velocities is observed for the period (1994.01.13–1994.01.19). Note one more feature is a gradual weakening of the northern anticyclone. Figure 7 demonstrates the weakening in the fields of all parameters under consideration, and Figure 8 confirms it with negative values of the $KmKe$ flux (a reverse cascade).
It is a very sophisticated task to observe the interaction of mesoscale eddies using in situ data. There are various reasons, which prevent obtaining such observations for any areas of the World ocean. Mesoscales of eddies and difficulties with eliminating other located closely structures are just two of them. A compromise solution can be the use of reanalysis data, especially those where in situ data are assimilating. We use reanalysis GLORYS 12v1 relevant for the study of vortex interaction because the data assimilation allows us to consider the natural processes maximal close to Nature.
In the current paper, we consider two situations of the vortex interaction: merging and splitting of eddies. We analyze the spatial distributions of SLA, the current velocities, the kinetic energy, the relative vorticity, and the Okubo-Weiss parameter spatial distributions. Time series of the spatial distributions of the parameters demonstrate the transformation of eddies during its interaction. The kinetic energy flows ($KmKe$) provide to study vortex interactions in terms of turbulent viscosity. The approach based on the analysis of spatial distributions of $KmKe$ during the eddy interaction is rather new.
Isachsen [2011, 2015] analyzed vortex generation in the context of baroclinic instability of the NASC. Dong et al. [2007] considered $KmKe$ flux in case of the influence of natural obstacle (an island) on a current. It also leads to the baroclinic instability of the current and eddy generation. Kamidaira et al. [2017] studied $KmKe$ in the Kuroshio current and estimate energy conversions from background flow to vortices in baroclinic instability. In all cases, these studies described the situations when the averaging window width is larger than generated vortices and the sources of its generation are relatively localized. We described the situations in the other conditions: there were no straight flow in the field of interaction and $KmKe$ flux characterizes interactions between more stable and less stable structures. More stable structures on the spatial distributions of the $KmKe$ flux are positive and transfer energy to the pulsations.
Our approach is somewhat different. We determine that the interpretation of the $KmKe$ assessments are closely connected with the averaging window width $T$. We reveal that an optimal window width for mesoscale processes is 3 or 7 days (see Figure 2). In this case, the energy exchange between more stable and less stable structures is observed well. It allows us to analyze characteristics of eddy interaction more detailed hence we should talk about the energy flows between more stable vortex structures and deformation elements. On the contrary, when the window width is 90 days, not only the background flow is averaged, but also the pulsations themselves. The application of $KmKe$ in the context of vortex interaction has not used previously.
We demonstrate the area of relative vorticity consists of three parts during the merging of eddies. $KmKe$ is positive in the external ring and in the central part of the eddy, which indicates the energy transfer to the structures of lower timescales. At the same time, $KmKe$ is negative in the middle ring of the eddy, which is between areas that were marked previously, which demonstrates the tendency to the stability of the structure (Figure 5). The positive values of $KmKe$ separate the vortex while it splits into two parts (Figure 7). Thus, $KmKe$ contributes to merging or splitting vortexes differently.
Alexeev, V. A., V. V. Ivanov, I. A. Repina, et al. (2016) , Convective structures in the Lofoten Basin based on satellite and Argo data, Izv. Atmos. Ocean. Phys., 52, no. 9, p. 1064–1077, https://doi.org/10.1134/S0001433816090036.
Bashmachnikov, I., T. Belonenko, P. Kuibin, et al. (2018) , Pattern of vertical velocity in the Lofoten vortex (the Norwegian Sea), Ocean Dynamics, 68, no. 12, p. 1711–1725, https://doi.org/10.1007/s10236-018-1213-1.
Bashmachnikov, I. L., T. V. Belonenko, P. A. Kuibin (2017a) , The application of the theory of the columnar Q-vortex with helical structure to the description of the dynamic characteristics of the Lofoten vortex of the Norwegian sea, Vestn. St. Petersburg Un-ta, Earth Sciences, 62, no. 3, p. 221–336, https://doi.org/10.21638/11701/spbu07.2017.301 (in Russian).
Bashmachnikov, I. L., et al. (2017b) , On the vertical structure and stability of the Lofoten vortex in the Norwegian Sea, Deep-Sea Res. I, 128, p. 1–27, https://doi.org/10.1016/j.dsr.2017.08.001.
Belonenko, T. V., I. L. Bashmachnikov, et al. (2017) , On the Vertical Velocity Component in the Mesoscale Lofoten Vortex of the Norwegian Sea, Izvestiya, Atmospheric and Oceanic Physics, 53, no. 6, p. 641–649, https://doi.org/10.1134/S0001433817060032.
Blindheim, J., S. \Osterhus (2013) , The Nordic Seas, Main Oceanographic Features, The Nordic Seas: An Integrated Perspective, H. Drange, T. Dokken, T. Furevik, R. Gerdes and W. Berger (eds.), p. 11–39, American Geophysical Union (AGU), Washington D.C, https://doi.org/10.1029/158GM03.
Bloshkina, E. V., V. V. Ivanov (2016) , Convective structures in the Norwegian and Greenland Seas based on simulation results with high spatial resolution, Proceedings of the Hydrometeorological Research Center of the Russian Federation, 361, p. 146–168 (In Russian).
Broecker, W. (1991) , The Great Ocean Conveyor, Oceanography, 4, no. 2, p. 79–89, https://doi.org/10.5670/oceanog.1991.07.
Carton, X. (2001) , Hydrodynamical modeling of oceanic vortices, Surveys in Geophysics, 22, no. 3, p. 179–263, https://doi.org/10.1023/A:1013779219578.
Chen, Y., J. Karstensen, et al. (2019) , Representation of selected mesoscale eddies in the eastern tropical Atlantic in an ocean re-analysis model and in a 3D ocean reconstruction, Geophysical Research Abstracts, 21, p. EGU2019-17929-1.
Dong, C. D., J. McWilliams, A. F. Shchepetkin (2007) , Island wakes in deep water, Journal of Physical Oceanography, 37, p. 962–981, https://doi.org/10.1175/JPO3047.1.
Fedorov, A. M., I. L. Bashmachnikov, T. V. Belonenko (2019) , Winter convection in the Lofoten Basin according to ARGO buoys and hydrodynamic modeling, Vestn. St. Petersburg Un-ta, Earth Sciences, 64, no. 3, p. 491–511, https://doi.org/10.21638/spbu07.2019.308 (In Russian).
Isachsen, P. E. (2011) , Baroclinic instability and eddy tracer transport across sloping bottom topography: How well does a modified Eady model do in primitive equation simulations?, Ocean Modell., 39, p. 183–199, https://doi.org/10.1016/j.ocemod.2010.09.007.
Isachsen, P. E. (2015) , Baroclinic instability and the mesoscale eddy field around the Lofoten Basin, J. Geophys. Res., 120, no. 4, p. 2884–2903, https://doi.org/10.1002/2014JC010448.
Isern-Fontanet, J., E. García-Ladona, J. Font (2003) , Identification of marine eddies from altimetric maps, Journal of Atmospheric and Oceanic Technology, 20, no. 5, p. 772–778, https://doi.org/10.1175/1520-0426(2003)20%3C772:IOMEFA%3E2.0.CO;2.
Kamidaira, Y., Y. Uchiyama, S. Mitarai (2017) , Eddy-induced transport of the Kuroshio warm water around the Ryukyu Islands in the East China Sea, Continental Shelf Research, 143, p. 206–218, https://doi.org/10.1016/j.csr.2016.07.004.
Köhl, A. (2007) , Generation and Stability of a Quasi-Permanent Vortex in the Lofoten Basin, J. Phys. Oceanogr., 37, p. 2637–2651, https://doi.org/10.1175/2007JPO3694.1.
Kurian, J., F. Colas, X. Capet, et al. (2011) , Eddy properties in the California current system, J. Geophys. Res.: Oceans, 116, p. C08027, https://doi.org/10.1029/2010JC006895.
Lozier, M. S. (2010) , Deconstructing the Conveyor Belt, Science, 328, no. 5985, p. 1507–1511, https://doi.org/10.1126/science.1189250.
Okubo, A. (1970) , Horizontal dispersion of floatable particles in the vicinity of velocity singularities such as convergences, Deep Sea Research and Oceanographic Abstracts, 17, no. 3, p. 445–454, https://doi.org/10.1016/0011-7471(70)90059-8.
S\oiland, H., L. Chafik, T. Rossby (2016) , On the long-term stability of the Lofoten Basin Eddy, J. Geophys. Res. Oceans, 121, p. 4438–4449, https://doi.org/10.1002/2016JC011726.
Starr, V. (1966) , Physics of Negative Viscosity Phenomena. Earth and Planetary Science Series Earth and Planetary Science Series, 256 pp., McGraw-Hill, New York.
Volkov, D. L., A. A. Kubryakov, R. Lumpkin (2015) , Formation and variability of the Lofoten basin vortex in a high-resolution ocean model, Deep-Sea Res. I, 105, p. 142–157, https://doi.org/10.1016/j.dsr.2015.09.001.
Volkov, D. L., T. V. Belonenko, V. R. Foux (2013) , Puzzling over the dynamics of the Lofoten Basin - a sub-Arctic hot spot of ocean variability, Geophys. Res. Lett., 40, no. 4, p. 738–743, https://doi.org/10.1002/grl.50126.
Weiss, J. (1991) , The dynamics of enstrophy transfer in two-dimensional hydrodynamics, Physica D: Nonlinear Phenomena, 48, no. 2–3, p. 273–294, https://doi.org/10.1016/0167-2789(91)90088-Q.
Zhmur, V. V. (2011) , Mesoscale Vortices of the Ocean, 384 pp., GEOS, Moscow (in Russian).
Received 24 May 2019; accepted 18 November 2019; published 16 March 2020.


Citation: Fedorov Aleksandr M., Tatyana V. Belonenko (2020), Interaction of mesoscale vortices in the Lofoten Basin based on the GLORYS database, Russ. J. Earth Sci., 20, ES2002, doi:10.2205/2020ES000694.
Copyright 2020 by the Geophysical Center RAS.