
RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 20, ES1004, doi:10.2205/2019ES000699, 2020
Renata Lukianova1,2, Alexander Kozlovsky3
1Geophysical Center of RAS, Moscow, Russia
2St. Petersburg State University, Institute of Earth Science, St. Petersburg, Russia
3Sodankylä Geophysical Observatory, Sodankylä, Finland
We use measurements of the ionospheric electron density ($N_e$) obtained by the EISCAT Svalbard radar (ESR) and the Sodankyla Geophysical Observatory (SGO) ionosonde for comparison with the $N_e$ distribution predicted by a numerical model of the polar $F$ region ionosphere. The model enables representing the main large-scale ionospheric irregularities, which are primarily controlled by the interplanetary magnetic field, particle precipitation, solar zenith angle and properties of the neutral atmosphere. The analysis utilizes the data collected in March, July and January under very quiet space weather conditions, when the radar operated almost continuously during International Polar Year. The main ionospheric parameters (magnitude and height of the $F2$ layer peak density) are inferred from the $N_e$ composites constructed for each local time hour. The results indicate that the modeled $N_e$ distributions are in a reasonable agreement with the experimental data. However, the modeled altitude and peak density systematically exceed, by about 10%, the observed values.
The $F$-region high-latitude ionosphere is the most complex and irregular because it is connected to the outer magnetosphere which interacts with variable solar wind. Besides ion production by photoionization and chemical losses due to recombination the additional factors determining the polar ionosphere include plasma dynamics and sporadic precipitation of energetic particles from the magnetosphere occurring mostly within the auroral oval. The transport processes play an important role in the high latitudes. The polar $F$ region plasma distribution is affected by the convection electric field which is imposed on the ionospheric shell from the magnetosphere and, together with the corotation electric field, makes the plasma tubes to drift along the lines of equal electrostatic potential. A parcel of plasma may become severely distorted after being displaced along convection streamlines for several hours through the illuminated and dark ionosphere as well as through the regions of enhanced ionization rate due to precipitation. The high-latitude convection pattern is controlled by the solar wind-magnetosphere interaction and thus primarily depends on the interplanetary magnetic field (IMF) orientation and strength [Heppner and Maynard, 1987; Lukianova and Chirstiansen, 2006; Papitashvili and Rich, 2002; Ruohoniemi and Greenwald, 2005]. Thermospheric neutral gas composition and temperature also affect the ionospheric parameters. Under common action of these processes the large-scale irregularities of the electron density ($N_e$), such as tongue of ionization (ToI), main ionospheric trough (MIT), polar hole, polar and auroral peaks are formed.
Despite a number of existing and recently deployed more sensitive and sophisticated instruments the polar ionosphere still remains rather poorly observed and not fully modeled. Because of lack of sufficient spatial/temporal resolution of the space and ground-based measurements the global empirical ionospheric models based on all available ionosonde and radio occultation electron density data, such as the International Reference Ionosphere, IRI [Bilitza et al., 2014], do not capture precisely the high-latitude variability, especially the polar cap features are less reproduced [Themens et al., 2014, 2017]. On the other hand, in the numerical models of the polar $F$ region which are based on the theoretical consideration, the ionospheric signatures associated with high latitude plasma convection and particle precipitation may be identified in more detail [Decker et al., 1994; Mingalev et al., 1988; Namgaladze et al., 1988; Ridley et al., 2006; Schunk, 1996; Sojka, 1989; Sojka and Schunk, 1987].
Several comprehensive global ionospheric models are available in the frame of the Community Coordinated Modeling Center (CCMC) (https://ccmc. gsfc.nasa.gov). In particular, the Global Assimilation of Ionospheric Measurements (GAIM) [Schunk et al., 2004] uses a physics-based model of the ionosphere and a Kalman filter as a basis for assimilating a diverse set of near real-time measurements. Its ionospheric part covers the $E$ and $F$-regions up to 1400 km. The Coupled Thermosphere Ionosphere Model (CTIM) [Fuller-Rowell et al., 1996] takes the electric potential and the electron precipitation parameters from the MHD magnetospheric model and provides in turn the conductances and the ionospheric dynamo current. The model output includes the ionospheric electric potential, field-aligned currents (FAC), the main electron parameters in the $F2$ layer, the neutral densities and composition. The NCAR Thermosphere-Ionosphere-Electrodynamics General Circulation Model (TIE-GCM) [Qian et al., 2014] represents the coupled thermosphere and ionosphere system that includes a self-consistent solution of the middle and low-latitude dynamo electric field. These global models among other parameters provide distribution of $N_e$ over the polar ionosphere. The calculations are based on quite sophisticated numerical codes and required a large amount of the computational resources. At the same time, a sufficiently precise and fast-running (capable to calculate the 3-D distribution of $N_e$ over the polar region in a second time-scale computer run) regional model specified for the $F$ region polar ionosphere is useful for the operational diagnosis and prediction of the space weather effects.
A numerical model specified for the high-latitude $F$ region ionosphere was developed [Uvarov and Lukianova, 2015]. This regional model (Polar $F$-region Ionospheric Model – PFIM) calculates the 3-D distribution of $N_e$ taking into account the IMF and solar wind conditions. The model is computationally effective and requires minimal resources/time. This is achieved mainly due to the analytical representation of the electric potential distribution continuously evolving with the solar wind parameters. The model simulation reproduces the main large scale ionospheric irregularities, it enables a quantitative estimation of the impact on the $N_e$ distribution of each particular input parameter [Lukianova et al., 2017].
PFIM develops the initial suggestion by Knudsen [1974] for a proper description of the polar ionosphere to solve transport equations along a magnetic plasma flux tube while it convects in the ionosphere due to ${\mathbf E} \times {\mathbf B}$ plasma drift. The advantages of PFIM as compared with other existing ionospheric models are primarily related to the explicit accounting of the convection electric field continuously depending on the solar wind parameters. Due to this, the model clearly displays the evolution of ionospheric irregularities with a change in the convection system. The input parameters can set directly from the solar wind observations. Also, the ionospheric response to the specific solar wind parameters, solar zenith angle, level of solar irradiance and geomagnetic activity can be identified. The drawbacks of the model are associated with its excessive schematism due to analytical approximations, inconsistent consideration of the auroral oval and some other over-simplifying assumptions. To obtain a more realistic representation, PFIM needs to be carefully compared with observations and further parameterized.
The purpose of this paper is to present the simulation results obtained by the numerical model of the polar $F$-region ionosphere during the solar minimum and prolonged geomagnetic quiescence ($Kp <1 $) associated with low values of the interplanetary magnetic field ($B_T < 5$ nT). These conditions can be considered to produce the ionospheric "ground state", when the role of the magnetosphere in the formation of the polar ionosphere is minimal. We have determined the seasonal patterns of ionospheric plasma distributions for March, July 2007 and January 2008. These periods correspond to extensive observational companies performed during the International Polar Year (IPY). Using the opportunity of the large date set the model is validated with observations of the EISCAT Svalbard radar (ESR), which is located near the polar cap boundary and operated nearly continuously during IPY. Also, the simulation results are compared with the Sodankyla ionozonde located in the vicinity of the equatorial boundary of the auroral oval. On the basis of the observed and modeled key ionospheric parameters: the maximum of electron density, $N_mF2$, and the height of this maximum, $H_mF2$ we reveal a possible ionospheric signature of the atmospheric cooling associated with an increase of the green-house gases.
 |
| Figure 1 |
The IPY period was at solar minimum, when the sunspot number almost zeroed and the solar index $F10.7 < 70$ sfu (1 s.f.u. = $10^{-22}$ Wm $^{-2}$ Hz$^{-1}$). As a result, the geomagnetic activity was low and no magnetic storm occurred during this time interval. The space weather conditions during the IPY period are very similar to those during the present solar minimum of 2018–2019. Figure 1 depicts the sunspot number, $F10.7$, $Dst$ and $Kp$ indices since 1999 (the beginning of the radar observations at Svalbard).
 |
| Figure 2 |
From the IPY observational period in 2007–2008 we selected the months representing 3 seasons, namely the equinox, summer and winter. Figure 2 depicts the solar wind and geomagnetic conditions in March 2007, July, 2007, and January 2008. During these periods, considerable recurrent activity lasted entire year 2007 and 2008, because the solar activity was dominated by the high speed streams (HSS) accompanied by an increase in the IMF intensity (BT) up to about 8 nT, while the non-HSS level is about 3 nT. As seen in Figure 2 the solar wind speed periodically oscillates between approximately 300 and 600 km/s. The geomagnetic activity varies in accordance with the solar wind speed and the $Kp$ index grows up to 4, if the speed increases.
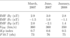 |
| Table 1 |
For each month the quiet days were selected according to the following criteria: $B_T =\sqrt{B_z^2 +B_y^2} < 5$ nT, $V_{\mathrm{sw}} < 400$ km/s, $Kp < 2$. Overall, 11, 13 and 10 days are selected in March, July and January, respectively. The solar, IMF and geomagnetic parameters averaged over each period are listed in Table 1. The observations collected during the selected days are used to calculate the $N_e$ quiet-time altitudinal profile composite for the corresponding month. Usually very dynamic, during these periods the polar ionosphere is significantly less variable. This may minimize the inhered uncertainties introduced by the averaging.
The input parameters of the PFIM are the IMF $B_z$ and $B_y$ components, the solar wind speed, day of the year, universal time, indices of solar ($F10.7$) and geomagnetic ($Kp$) activity. The model output is 3-D distribution of $N_e$ over the ionospheric $F$ region poleward of 50° magnetic latitude (MLat) with nominal vertical step of 10 km between 150 and 600 km on the horizontal grid of 2° MLat and 15° magnetic longitude (MLong), respectively.
The model consists of two interrelated blocks representing the transport and chemical processes. The height distribution of the plasma density at a given UT is a result of the cumulative effect of convection and corotation acting on the sources of ionization and recombination over the previous several hours. The resulting $N_e$ distribution depends on the time interval the convecting plasma flux tube spends in the sunlit, dark and particle precipitation regions. As a first step, for a given time and geographical point the trajectory is calculated back in time to determine the starting point at from which a plasma tube begins to convect. In the present version of the model, it is assumed that the solar wind and geomagnetic activity are stable when calculating the plasma tube trajectories back in time. The 8-hr period is taken to establish the zero initial conditions from which a plasma tube is traced along its trajectory through a neutral atmosphere. At the second step, numerical solution of the equations describing the vertical plasma distribution within the tube is carried out while the tube drifts from the starting point along the calculated trajectory.
In the first, convective, block of the model the geometric and electrodynamic parameters of the ionospheric convection pattern are calculated in order to determine the trajectories along which the plasma tubes move. It is assumed that the electric field is mapped vertically with no distortion. When calculating the electric field distribution, the ionosphere is approximated as a thin shell at about 200 km altitude. In the geomagnetic spherical coordinates $r$, $\theta$, $\varphi$ ($r$ is radius, $\theta$, is colatitude, $\varphi$ is magnetic longitude) the velocity of the charged particle is a sum of the corotation velocity $V_K = (0, 0, \omega \,r \,\sin \theta$) and the electromagnetic drift velocity in the transverse electric ($\mathbf E$) and magnetic ($\mathbf B$) fields. The differential equations determining the transverse components of drift velocity are
\begin{eqnarray*} \frac{\partial \theta}{\partial t} = -2 E_{\varphi} (\theta, \varphi) \: \frac{(R^2/M) \cos \theta}{3\cos\theta + 1} \end{eqnarray*} \begin{eqnarray*} \frac{\partial \varphi}{\partial t} = E_{\theta} (\theta, \varphi) \: \frac{R^2/M}{3\cos\theta \sin\theta} + \omega \end{eqnarray*}where $M$ is the Earth's magnetic moment, $\omega$ is the Earth's angular frequency, $R = R_{\mathrm E} + 200$ km, $R_{\mathrm E}$ is the Earth's radius, $t$ is time, $E_\theta$ and $E_\varphi$ is the latitudinal and azimuth component of the horizontal ionospheric electric field $\mathbf E$.
In the modeling approach the ionospheric electric potential is driven by the field-aligned currents (FACs) generated in the magnetosphere and flowing between the magnetosphere and ionosphere along the geomagnetic field lines. The equation of electric current continuity and the relationship between the ionospheric current and electric potential is
\begin{equation} \tag*{(1)} \mathrm{div}\, {\mathbf J} = j \sin \chi, \quad {\mathbf J} = \sigma \, (- \nabla U) \end{equation}where $\mathbf J$ is the height-integrated horizontal ionospheric current, $j$ is the radial component of FAC, $\chi$ is magnetic inclination, $U$ is the electrostatic potential and $\sigma$ is the height-integrated conductivity tensor including both the Hall and Pedersen ionospheric conductivities.
The electric field distribution depends on the FAC topology which is based on the Region 1, 2 and 3 classification introduced by Iijima and Potemra [1976]. The entire system of FAC sheets, stretched along the latitudinal circles, is decomposed into subsystems which are separately controlled by the IMF $B_z$ and $B_y$ components. Additional parameterizations are used to account for the influence of IMF strength on the latitudinal shift of ionospheric footprint of the FAC sheets and clockwise rotation of the convection pattern. The FAC and electric potential distributions over the ionospheric shell are represented by analytical functions allowing their continuous evolution following the solar wind parameters, UT and season.
If the IMF is purely southward ($B_z < 0$), the Region 1 and Region 2 FACs are assumed to be symmetric relative to the noon-midnight meridian and both FACs are approximated by the sine function at the entire MLT interval [$\pm \pi$]. The electric potential distribution is represented as
\begin{eqnarray*} U (\theta, \varphi) = -T(\theta) F(\varphi) \end{eqnarray*}where $F(\varphi) = \sin (\varphi - \varphi_0$) and $\varphi_0$ determines a rotation of the convection pattern relative to the noon–midnight meridian while the IMF strengthens. $T(\theta$) is calculated by integration the electric field distribution along the dawn-dusk meridian ($E_{\mathrm{dawn-dusk}}$).
If the IMF northward ($B_z > 0$), the FACs are transformed into the sheets confined to 09:00–15:00 MLT poleward of the Region 1 and are directed oppositely to the Region 1 FACs. These FACs are approximated by the Fourier series of sine function at [$\pm \pi/2]$
\begin{eqnarray*} j(\varphi) = \sum_m \: (j_m \sin (m\varphi)) \end{eqnarray*}where $j_m$ is the $m$ Fourier coefficient.
The corresponding electric potential distribution is
\begin{eqnarray*} U (\theta, \varphi) = \sum_m \: [\theta^m (A_m \cos (m\varphi) + \end{eqnarray*} \begin{eqnarray*} B_m \sin (m \varphi))] \end{eqnarray*}An independent Region 3 FAC system is controlled by the IMF $B_y$ component. These FACs are also confined to 09:00–15:00 MLT poleward of the Region 1 and approximated by the cosine function at [$\pm \pi/2]$ with current flowing into (from) the northern ionosphere, if $B_y$ is negative (positive). The expression for the FAC density is
\begin{equation} \tag*{(2)} j(\varphi) = \sum_m \: (j_m \cos (m\varphi)) \end{equation}The solution of (2) within the northern polar cap $(\theta < \theta_{pc}$), where the geomagnetic field lines are open, and in the region equatorward of the polar caps $(\theta > \theta_{pc}$), where the geomagnetic field lines are closed, is written, respectively, as
\begin{eqnarray*} U (\theta, \varphi) = -\frac{\theta_\mathrm{pc} j_0}{\sigma_\mathrm{pc}} \ln \frac{\theta_\mathrm{pc}}{\theta} + \end{eqnarray*} \begin{eqnarray*} \sum_m \: \big[\theta^m (A_m \cos (m\varphi) + B_m \sin (m \varphi))\big] \end{eqnarray*}and
\begin{eqnarray*} U (\theta, \varphi) = \sum_m \: \Bigl[ \frac{1}{\theta^m} (C_m \cos (m\varphi) + \end{eqnarray*} \begin{eqnarray*} D_m \sin (m\varphi))\Bigr] \end{eqnarray*}The coefficients $A$, $B$, $C$ and $D$ are calculated from the boundary conditions as follows. First, there is no discontinuity in the electric potential across the boundary of the polar caps $\theta_{\mathrm{pc}}$ on the ionospheric shell. Second, any possible discontinuities of the ionospheric currents across the boundaries of the northern and southern polar caps compensate each other through the currents leaking into the lower latitudes.
Analytical model of the electric field distribution over the high-latitude ionosphere is based on the profiles of $E_{\mathrm{dawn-dusk}}$ which continuously evolves with the solar wind parameters. The topology (geometrical shape) of $E_{\mathrm{dawn-dusk}}$ profile is determined by the IMF $B_z$ and $B_y$ signs while its magnitude within a certain topology depends on the strength of each IMF components. An additional electric field originates from the dynamo action of neutral winds as $\mathbf{E = V}_{n} \times \mathbf{B}$, where $\mathbf{V}_{n}$ is the neutral wind velocity taken from the model by [Emmert et al., 2008]. The corresponding term is added to the right part of the second equation (1). Note that in the high latitudes the dynamo effect of winds is seems to be weak compared to the convection electric field.
In the ionospheric block of the model the time-dependent ion continuity and momentum equations are solved as a function of altitude within a convecting and corotating flux tube. The 1-D momentum equation (diffusive transport) for the major $F$ region species, the O$^+$ ion (3), and the continuity equation of photochemical equilibrium for the generalized molecular ion M$^+$ (4), which is produced due to the solar EUV and corpuscular ionization and the chemical reactions with O$^+$, are integrated along the convection trajectories.
\begin{eqnarray*} \frac{\partial}{\partial t} n(\mathrm{O}^+) = \end{eqnarray*} \begin{equation} \tag*{(3)} \frac{\partial}{\partial z} \left( F \frac{\partial}{\partial z} n(\mathrm{O}^+) + R n(\mathrm{O}^+) \right) + Q_{\mathrm{O}^+} - L \end{equation}where $n$(O$^+$) is the ion concentration, $t$ is time, $z$ is altitude, $F$ and R are the coefficients obtained from the expressions for the vertical velocity of O$^+$, $Q_{\mathrm O^+}$ and $L$ are the ion production and loss rates, respectively. For the O$^+$ ion, two main chemical reactions with O$_2$ and N$_2$ are taken into account.
\begin{equation} \tag*{(4)} Q_\mathrm{M^+} + L = \alpha n(\mathrm{M}^+) \, (n(\mathrm{M}^+) + n(\mathrm{O}^+) \end{equation}where $\alpha$ is the recombination coefficient.
The auroral oval is considered as a statistical one and precipitating particle characteristics are taken from the empirical model based on the precipitation spectra observed by the DMSP satellites [Hardy et al., 1987]. The bottomside boundary conditions for the ion number density correspond to the photochemical equilibrium for O$^+$ and equal electron, ion and neutral temperatures. At high latitudes, plasma tubes are considered to act like open ones. At the topside boundary the O$^+$ outflow may occur due to an ambipolar diffusion (polar wind) which depletes the high-latitude ionosphere of its content of light ions and to some extent O$^+$ ions [David et al., 2018]. In the present version of the model, for simplicity, the upper boundary conditions at 600 km height do not allow ions to escape further to the magnetosphere.
The neutral atmosphere is not calculated but instead the semi-empirical MSIS-family [Hedin et al., 1991] thermosphere model, NRLMSISE-00 [Picone et al., 2002] is employed to estimate the spatial distribution of the number densities and temperatures of the major thermospheric neutral components N$_2$, O$_2$ and O which are ionized by energetic particle precipitation and solar direct and scattered radiation.
 |
| Figure 3 |
Example of the model output is presented in Figure 3 as the contour map of the $N_e$ peak values ($N_mF2$) for the following representative input parameters: IMF $B_z = -3$ nT, $B_y=0$, UT$ \:=\,$11:00, DOY$\:=360$. To demonstrate the critical role of the plasma convection in forming the large scale ionospheric irregularities, the $N_mF2$ contours are superimposed on the corresponding isolines of the electrostatic potential $U$ (red lines). If IMF $B_z$ is directed southward ($B_z < 0$), the ionospheric projection of the magnetospheric plasma circulation is a two-cell convection pattern with a fairly homogenous central antisunward flow and with a return flow along the dawn and dusk portions of the auroral oval. The corotation electric field drives the round-pole plasma drift. Superposition of the symmetric two-cell convection pattern and the one-cell corotation pattern results in an asymmetry. Due to corotation effect, the dawn cell becomes larger, while the dusk cell is suppressed and the antisunward plasma flow channel is shifted to the dusk side. Some plasma tubes move anticlockwise along the equatorial boundary of the high latitude region, then enter the dusk side convection cell and then form the cross polar antisunward flow. The plasma tube trajectories partly stagnate in the post-noon local time sectors likely because the convection velocity just balances the corotation one.
The $N_mF2$ distribution presented in Figure 3 is typical for the winter polar ionosphere under conditions of IMF $B_z \leq 0$ and relatively low particle precipitation. The largest $N_e$ is observed in the post-noon sector whose ionospheric plasma has been long illuminated while drifted on the day side. A considerable increase in $N_e$ up to $3 \times 10^{11}$ m$^{-3}$ at $\sim 60\mbox{°}$ MLat forms the polar peak in which the plasma density may additionally increase due to convective stagnation of the plasma tubes. The enhanced $N_e$ extends from the day side to the night side due to the transpolar anti-sunward plasma flow. The polar cavity is manifested by a decrease in $N_e$ lower than elsewhere in the polar cap in the post-midnight local time sector in darkness. The central part of ToI is suppressed by the polar cavity, so that it tends to split up into two branches.
 |
| Figure 4 |
The 3-D distribution of $N_e$ within the $F$ region polar ionosphere is modeled on the hourly basis and then averaged over a whole quiet period of each month. The input parameters are taken according to Figure 2. Maps of the $N_mF2$ isolines in the MLT–MLat coordinate system are presented in Figure 4. From this figure one can identify several large-scale $F$-region irregularities and follow its seasonal evolution. The dark winter ionosphere is almost empty of plasma, the equinoctial ionosphere is characterized by the largest spatial gradients of plasma density and the summer ionosphere is the most homogeneous. The systematic change in the $F$-layer peak density is such that the magnitude of the post-noon peak increases from winter ($ \sim 1.5 \times 10^{11}$ m$^{-3}$) through summer ($ \sim 2.5 \times 10^{11}$ m$^{-3}$) to equinox ($ \sim 3 \times 10^{11}$ m$^{-3}$). The dayside $N_e$ enhancement tends to extend to the nightside due to the antisunward transpolar plasma flow which is strong enough even under zero IMF $B_z$ conditions. However, in the central polar cap the polar cavity tends to dominate, so that ToI is shifted to the flanks. The polar edge of MIT and the auroral peak are reproduced in winter and equinoctial ionosphere.
In this paper we utilize a large data set of the incoherent scatter EISCAT Svalbard radar (ESR, 78.2° N, 16.0° E) collected in 2007–2008 to compare the observed and modeled monthly composites of the key parameters of $N_e$ distributions over three seasons (equinox, summer and winter), based on unprecedented data set from the ESR collected during International Polar Year (IPY) when the ESR was operating nearly continuously. This formed a valuable dataset of basic ionospheric parameters, collected under very low solar and magnetic activity conditions, which represent a background state of the ionosphere. The IPY data collection has been used extensively to address some fundamental questions about upper atmosphere climatology [Sojka et al., 2007; Zhang et al., 2010].
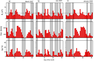
 |
| Figure 5 |
The EISCAT radars are able to probe the ionosphere by transmitting a signal and receiving back-scattered signals [Williams, 1995]. The radar measures the basic plasma parameters of the ionosphere including $N_e$, electron and ion temperature and the l-o-s velocity. We got the data from the MADRIGAL online database, which contains analyzed ESR data starting from the beginning of the radar operation in 1996. During IPY, from March 2007 to February 2008, the ESR 42 m dish operated almost continuously making the field-aligned measurements (azimuth 184.0°, elevation 82.1°) called the CP1 mode. ESR measurements cover more than 60% of the total time within the IPY campaign (note, in 2009, because measurements are conducted usually as short campaigns, the corresponding time fraction was only $\sim 2$%). The valuable data set was collected under very low solar and magnetic activity conditions. Detailed information about the data coverage is given in Figure 5. In March and July, 2007 measurements are available for about 80% of each month. The period of January 2008 has more data gaps and the data may be of lower quality, mostly because the plasma in polar winter ionosphere was so rarefied that the radar was able to receive only very few scatter signal.
We took the opportunity of the IPY long-term ESR run to construct a composite of the $N_e$ height profiles for each MLT from a large database. In the IPY mode, the data are collected with 1 minute resolution. In order to eliminate the short-term fluctuations, a running mean averaging was performed every 5 minutes, over periods of 60 minutes. The altitude step is 5–15 km, 15–20 km, and 20–30 km for altitudes 150–200 km, 200–300 km, and $ > 300$, respectively. The monthly ESR $N_e$ composites for each local time hour are used for comparison with the $N_e$ predicted by PFIM.
 |
| Figure 6 |
Performing a series of model simulations we collect the $N_e$ height profiles over the ESR site and then calculate a composite. Similar composites are constructed using the ESR data. The 2-D distributions of log($N_e$) (in the frame of height versus MLT) over the ESR site representing the three different seasons are shown in Figure 6. The upper and lower plots show the actually observed and simulated log($N_e$), respectively.
During the quiet period with a stable $F10.7$ level, the $N_e$ distributions exhibit more likely the undisturbed seasonal trend. In the polar ionosphere, $N_e$ exhibits a deep minimum in winter when the sun is always set. The electron density does not reach maximum in summer as would be expected from photochemical processes; instead, both the observed and modeled $N_e$ tend to be the largest in spring. The observed (modeled) peak log($N_e$) contour is equal to 11.4 (11.6), 11.4 (11.5), 11.0 (11.0) for the equinoctial, summer and winter month, respectively.
The shape of the height profiles do not coincide so well at each particular local time and season. For example, in July, even visual examination of the corresponding upper and lower plots in Figure 6 reveals that the model predicts stronger spatial gradients in plasma density, while the actually observed distributions are more homogenous. Another notable difference is that PFIM systematically underestimates $N_e$ in the upper part of the height profiles. This reduction may be due to the simplified upper boundary conditions, which do not account for the escape of the oxygen due to the polar wind. The largest discrepancy in the isolines of $N_e$ is observed in January. The modeled $N_e$ reaches its maximum in the post-noon sector, while the observed $N_e$ peak is shifted to the later local times. In March and July the positions of the dayside maxima match well.
 |
| Figure 7 |
The key parameters of the $N_e$ distribution are the $N_e$ peak ($N_mF2$) and its height ($H_mF2$). The quantitative estimate of the PFIM performance relative to the observational results is shown in Figure 7. Although the model predicts slightly larger $N_mF2$, the modeled and observed $N_e$ peaks match closely. The difference between the two techniques does not exceed 15% and decreases going from the equinoctial/summer to the winter months. The modeled heights of the $N_e$ maximum are considerably larger than those observed by the radar. The model predicts 280, 270 and 285 km, while the ESR $H_mF2$ is 240, 238 and 247 km for March, July and January, respectively. Thus the systematic difference is about 40 km for all months under consideration.
To compare the modeled $N_e$ at the auroral latitudes we utilize the data collected by the Sodankyla Geophysical Observatory (SGO, 67.2° N, 26.6° E) ionosonde [Kozlovsky et al., 2013]. Since April 2007, at SGO, a frequency-modulated continuous-wave chirp ionosonde operates performing one sounding per minute. The critical frequency (the highest magnitude of frequency above which the waves penetrates the ionosphere) of the $F2$ layer ($f_oF2$) is routinely measured by ionospheric vertical sounders. These data provide a reliable estimation of the $N_e$ peak ($N_mF2$). The $f_oF2$ measured by an ionosonde can be converted to $N_mF2$ by
\begin{eqnarray*} N_mF2 = \frac{\varepsilon_0 m_e 4 \pi^2}{e^2} \: (f_o F2)^2 \end{eqnarray*}where the unit for $N_mF2$ is m$^{-3}$, and that for $f_oF2$ is Hz.
 |
| Figure 8 |
From the original 1-hr values of $f_oF2$ the monthly medians of $N_mF2$ are calculated. Then the $N_mF2$ data are sorted as a monthly composite for each local time hour (MLT = UT$\:+3$ for the Sodankyla site). The monthly averages (median values) of ionospheric parameters are the standard parameters in the ionosonde data set of the International Union of Radio Science (URSI). The data are related to MLat$\:=64.1\mbox{°}$, $L=5.25$, it is close to the southern boundary of the auroral oval. Comparison of the model output with the SGO ionosonde measurements is based on the monthly median values of $f_oF2$ for the same periods as the ESR observations. Figure 8 depicts the diurnal variations of the $N_mF2$ median for January, March and July. Each panel presents a combination of the experimental and simulated daily curves.
From Figure 8 one can see that during daytime the magnitude and shape of the simulated daily curves are in reasonable agreement with observations, while the model systematically overestimate the nighttime $N_mF2$ by about $0.5 - 1 \times 10^{11}$ m$^{-3}$. The discrepancy is likely related to a stronger effect of auroral particle precipitation in the model. In winter/equinox, the observed and modeled daytime $N_mF2$ values are of the similar amplitude (2 and $3 \times 10^{11}$ m$^{-3}$ for January and March, respectively) and of the close local time position (14:00 and 15:00 MLT). In summer, when the ionosonde daily curve is rather flat, the model predicts a pronounced difference between the day- and nighttime $N_mF2$ as well as a shift of the daytime peak to the later MLTs. In July the modeled night time $N_mF2$ is by about $0.5 \times 10^{11}$ m$^{-3}$ lower than the observed one. Showing the same seasonal effect as the ESR observations, the equinoctial daytime peak slightly exceeds the summer peak. Overall, comparison of the modeling results and the ionosonde measurements confirms the tendencies seen in the ESR observations.
Physical models based on the governing equations are limited by the inherent schematic representation of key parameters and thus need validation and direct comparison with the experimental data. To take this step the simulated data from PFIM model have been validated against measurements of the Svalbard ESR located in the polar cap (75° MLat) and the SGO ionosonde located in the auroral zone (64° MLat). A quantitative test of the model predictions is based on the large set of observations made during IPY, when the solar cycle was at its minimum and the high-latitude ionosphere was relatively undisturbed. However, although the sunspot number was very low, the solar activity was dominated by the solar wind HSSs, during which the substorm occurrence may be greatly enhanced [Lukianova et al., 2012; Mursula et al., 2015]. Because of this, HSS days were excluded from the analysis, which reduced the total number of days by about a half.
To assess the key parameters an analysis is performed of how the main large-scale ionospheric irregularities vary in morphology and magnitude with the local time and season. The results of comparison indicate that the modeled magnitude and height of $N_mF2$, the annual and diurnal variations are in general agreement with the experimental data. On the other hand, some discrepancies are revealed in the $N_e$ distributions inferred from the model and observations at particular heights and local times. In general, the model tends to underestimate $N_e$ at the heights above the $F2$ peak plasma density. In the following we concentrate on the possible reasons of disagreements, understanding of which will help to improve the PFIM in the future.
The discrepancy between the ESR observations and modeling becomes notable above $\sim 300$ km. It can be caused by the effect of the zeroed upper boundary conditions for the diffusion equation for O$^+$ used in the present version of PFIM. In the polar cap, where the length of the geomagnetic field line substantively increases, a flux tube becomes almost vertically oriented and open to the solar wind. At the upper boundary (at 600 km) of the modeled ionospheric slab, it is more realistic to set the slope of the O$^+$ density, which is related to the flux of ions across the boundary. However, because of the low geomagnetic activity, the model run is performed under assumption of the zero ion outflow. David et al. [2018] using the ESR observations during the IPY 2007 period have investigated the diurnal and seasonal variability of the ion fluxes at the $F$ region altitudes at various levels of geomagnetic activity. It was shown that the high-flux upflow events are to be a rare occurrence while the low-flux events are a much more frequent phenomenon. During solar minimum, a lower magnitude of upflow occurrence, less than $2.5 \times 10^{13}$ m$^{2}$ s$^{-1}$, has been observed. Nevertheless, from the physical point of view this assumption may lead to the underestimate of the calculated $N_e$ above the peak height.
Simulated distributions shown in Figure 6 reveal a notable depletion (polar cavity) in the nighttime $N_e$, while the depletion observed by the ESR radar is much smaller. The polar cavity is primarily associated with the convection reversal in the regions of weak convection, while ionization chemical decay progressed [Benson and Grebowsky, 2001; Sojka et al., 1991]. The downward drift component (associated with the dawn-dusk electric field within the polar cap) which increases the ion outflow into the region with a larger neutral density and, correspondingly, with a higher rate of recombination may play a role [Rishbeth and Garriott, 1969]. Taking into account the mechanisms of the polar cavity formation, the discrepancy between the observed and modeled morphology of the night-time $N_e$ distributions may be related to a simplified analytical expressions of $E_{\mathrm{dawn-dusk}}$. In particular, the analytical representation may overestimate the night side electric potential, when the IMF $B_z$ rotates from south to north and the topology of the $E_{\mathrm{dawn-dusk}}$ profile is changed. It is related to the fact that the basic convection pattern is assumed to be symmetric relative to the dawn-dusk meridian and the foci of the convection vortices are not shifted sunward if the IMF $B_z$ becomes northward. Comprehensive convection models have shown more complicated dependence of the convection patterns on the polarity of IMF and the solar zenith angle [Lukianova et al., 2008; Ruohoniemi and Greenwald, 2005; Weimer, 2005; Zhang et al., 2007]. In particular, the sign of IMF $B_y$ and season introduce an asymmetry to the electric potential distribution. If $B_z$ turns northward and also with the advance of season from winter to summer, the convection cells appear to move antisunward. Fine convection structures are not accounted by PFIM, whose convection patterns more likely reproduce the basic signatures of Heppner and Maynard [1987].
Relatively good agreement is achieved between the simulated daily variation of $N_mF2$ and the ionosonde measurements made near the equatorial boundary of the auroral oval. However, although the daytime peak of $N_mF2$ is reproduced with high accuracy, in the night side the model predicts the higher values of $N_mF2$ compared to the ionosonde data. The source of this discrepancy is likely related to an overestimation of auroral particle precipitation in the model. The model is parameterized by the global $Kp$ index. The step in $Kp$ index is taken as one unit and the auroral characteristics are calculated for $Kp=1$ (see Table 1). However, in 2007–2008 the actual precipitation rate seems to be marginal.
On the day side, the simulated $N_e$ is in quantitative agreement with observations of both instruments. The model shows that the more dense plasma is concentrated in the post-noon local time sector at about 70° MLat. This irregularity is likely associated with the dayside polar peak. The polar peak is often attributed to the low energy electron precipitation in the cusp region although at markedly different altitudes depending on the energy [Cai et al., 2007; Millward et al., 1999]. However, in the PFIM model, the precipitating spectra and related parameters are taken from the model by Hardy et al. [1987] which does not specify the cusp precipitation. Thus the polar peak reproduced by the model is likely caused by the peculiarities of plasma drift in the post-noon sector, where the sunlit plasma tubes tend to stagnate due to the oppositely directed convection and corotation electric fields. Comparison of the observed and modeled main variables of the $F2$ region ionosphere: peak of electron density $N_mF2$ (and critical frequency $f_oF2$ as an equivalent to maximum electron density) and height of the peak, $H_mF2$, reveals that the model predicts a considerably higher altitude of $H_mF2$ and a slightly larger magnitude of $N_mF2$ than actually observed values. Since the influence of solar activity is very weak during the periods under consideration, we speculate that the origin of systematic difference of about 40 km is likely due to changes in the background atmosphere. In PFIM, the neutral atmosphere is represented by the NRLMSISE-00 model which is based on the previous member of the MSIS family, MSIS-90. The data underlying MSISE-90 cover the period 1965–1983. The expanded database contains observations up to 1997. Since that time, significant changes have occurred in the upper atmosphere mainly due to anthropogenic impact.
Comprehensive analysis of the long-term trends [Lastovichka et al., 2012 and references there in] has shown that at present long-term changes in the atmosphere-ionosphere system are predominantly controlled by the increasing concentration of greenhouse gases. Moreover, the greenhouse gas control of long-term changes in the ionosphere was increasing throughout the 20th century, while the solar and geomagnetic control was decreasing.
The radar observations revealed changes in ion temperature in the midlatitude upper thermosphere at 250–400 km height [Holt and Zhang, 2008; Zhang et al., 2011]: a cooling by $2.5-5$ K/year. The larger values are for higher altitudes. As pointed out by Lastovichka et al. [2012], the negative trend in the thermospheric ion temperatures together with a negative trend in the thermospheric neutral density indicates a negative trend in the thermospheric neutral temperature. Cooling and contraction of the upper atmosphere affect the neutral and ion composition because the majority of chemical reactions are temperature dependent. Model calculations of the effect of CO$_2$ doubling on the ionosphere by [Qian et al., 2008] have shown that in the high latitudes the combined effect of changes in photochemical and plasma transport processes together with thermal shrinking of the upper atmosphere result in a decrease of $H_mF2$ by about 20 km, while decrease of $f_oF2$ is relatively small. Negative trend of $N_e$ and the peak height in the $F2$ region due to cooling and contraction under greenhouse gas forcing is likely a reason of the systematic excess of the PFIM $N_e$ over the ESR observations.
The numerical model of the polar $F$ region ionosphere (PFIM) is developed in order to predict the main features and large scale ionospheric irregularities which are produced primarily by the plasma processes driven by magnetospheric dynamics and also depend on the background atmosphere.
Validation of the accuracy of the proposed modeling with real data has been made using measurements of ionospheric plasma density obtained by the European incoherent scatter (EISCAT) Svalbard radar (ESR, 78.2° N) and the SGO ionosonde (67.2° N) under quiet solar conditions of March and July 2007, and January 2008. The key parameters characterizing the polar ionosphere $F$ layer (magnitude and height of the $N_e$ peak, their daily and seasonal variations) are in reasonable agreement with the experimental data. The key parameters are seemed to be reproduced reliably, although the model predictions are in better agreement with the observations on the day side and below 300 km height.
Overall, the model by about 10% underestimates the ionospheric parameters as compared with actual measurements. Insufficiency and over-simplicity of the model may be a reason of the systematic excess of the PFIM $N_mF2$ and $H_mF2$ over the ESR observations. Besides, a negative trend in $N_e$ and height of the $F2$ region due to the upper atmosphere cooling and contraction under greenhouse gas forcing would lead to the same effect. However, further, more sophisticated study is needed to confirm/refute this assumption.
The datasets from the EISCAT ESR radar, the Sodankyla Geophysical Obsevatory ionosonde, the OMNI solar wind are available in the https://open madrigal.org/, http://www.sgo.fi/, https://omniw eb.gsfc.nasa.gov/.
Benson, R. F., J. M. Grebowsky (2001) , Extremely low ionospheric peak altitudes in the polar hole region, Radio Science, 36, no. 2, p. 277–285, https://doi.org/10.1029/1999RS002401.
Bilitza, D., D. Altadill, Y. Zhang, et al. (2014) , The international reference ionosphere 2012 – a model of international collaboration, Journal Space Weather Space Climate, 4, p. A07, https://doi.org/10.1051/swsc/2014004.
Cai, H. T., S. Y. Ma, Y. Fan, et al. (2007) , Climatological features of electron density in the polar ionosphere from long-term observations of EISCAT/ESR radar, Annales Geophysicae, 25, p. 2561–2569, https://doi.org/10.5194/angeo-25-2561-2007.
David, T. W., D. M. Wright, et al. (2018) , A study of observations of ionospheric upwelling made by the EISCAT Svalbard Radar during the International Polar Year campaign of 2007, Journal Geophysical Research Space Physics, 123, p. 2192–2203, https://doi.org/10.1002/2017JA024802.
Decker, D. T., C. E. Valladares, R. Sheehan, et al. (1994) , Modeling daytime F layer over Sondrestrom, Radio Science, 29, no. 1, p. 249–268, https://doi.org/10.1029/93RS02866.
Emmert, J. T., D. P. Drob, G. G. Shepherd, et al. (2008) , DWM07 global empirical model of upper thermospheric storm-induced disturbance winds, Journal Geophysical Research Space Physics, 113, p. A11319, https://doi.org/10.1029/2008JA013541.
Fuller-Rowell, T. J., D. Rees, et al. (1996) , A coupled thermosphere-ionosphere model (CTIM), STEP Report: Handbook of Ionospheric Models, R. W. Schunk (Ed.), p. 217–238, Center for Atmospheric Space Science, Utah State University, Logan Utah.
Hardy, D. A., M. S. Gussenhoven, R. Raistrick, et al. (1987) , Statistical and functional representations of the pattern of auroral energy flux, number flux, and conductivity, Journal Geophysical Research, 92, no. A11, p. 12,275–12,294, https://doi.org/10.1029/JA092iA11p12275.
Hedin, A. E., M. A. Biondi, R. G. Burnside, et al. (1991) , Revised global model of thermospheric winds using satellite and groundbased observations, Journal Geophysical Research, 96, no. A5, p. 7657–7688, https://doi.org/10.1029/91JA00251.
Heppner, J. P., N. C. Maynard (1987) , Empirical high-latitude electric field model, Journal Geophysical Research, 92, no. A5, p. 4467–4489, https://doi.org/10.1029/JA092iA05p04467.
Holt, J. M., S.-R. Zhang (2008) , Long-term temperature trends in the ionosphere above Millstone Hill, Geophysical Research Letters, 35, p. L05813, https://doi.org/10.1029/2007GL031148.
Iijima, T., T. A. Potemra (1976) , The amplitude distribution of fieldaligned currents of northern high latitudes observed by Triad, Journal Geophysical Research, 81, no. 13, p. 2165–2174, https://doi.org/10.1029/JA081i013p02165.
Knudsen, W. C. (1974) , Magnetospheric convection and the high latitude $F2$ ionosphere, Journal Geophysical Research, 79, p. 1046–1055, https://doi.org/10.1029/JA079i007p01046.
Kozlovsky, A., T. Turunen, T. Ulich (2013) , Rapid-run ionosonde observations of traveling ionospheric disturbances in the auroral ionosphere, Journal Geophysical Research, 118, no. 8, p. 5265–5276, https://doi.org/10.1002/jgra.50474.
Lastovicka, J., S. C. Solomon, L. Qian (2012) , Trends in the Neutral and Ionized Upper Atmosphere, Space Science Review, 168, p. 113–145, https://doi.org/10.1007/s11214-011-9799-3.
Lukianova, R., F. Christiansen (2006) , Modeling of the global distribution of ionospheric electric fields based on realistic maps of field-aligned currents, Journal Geophysical Research, 111, no. A3, p. A03213, https://doi.org/10.1029/2005JA011465.
Lukianova, R., C. Hanuise, F. Christiansen (2008) , Asymmetric distribution of the ionospheric electric potential in the opposite hemispheres as inferred from the SuperDARN observations and FAC-based convection model, Journal Atmospheric Solar-Terrestrial Physics, 70, p. 2324–2335, https://doi.org/10.1016/j.jastp.2008.05.015.
Lukianova, R., K. Mursula, A. Kozlovsky (2012) , Response of the polar magnetic field intensity to the exceptionally high solar wind streams in 2003, Geophysical Research Letters, 39, no. 4, https://doi.org/10.10029/2011GL050420.
Lukianova, R., V. M. Uvarov, P. Coisson (2017) , Evolution of the high-latitude F region large-scale ionospheric irregularities under different solar wind and zenith angle conditions, Advances Space Research, 59, no. 2, p. 557–570, https://doi.org/10.1016/j.asr.2016.10.010.
Millward, G. H., R. J. Moffett, et al. (1999) , Modeling the ionospheric effects of ion and electron precipitation in the cusp, Journal Geophysical Research, 104, p. 24603–24612, https://doi.org/10.1029/1999JA900249.
Mingalev, V. S., V. N. Krivilev, et al. (1988) , Numerical modeling of the high-latitude $F$-layer anomalies, Pure Applied Geophysics, 127, no. 2–3, p. 323–334, https://doi.org/10.1007/BF00879815.
Mursula, K., R. Lukianova, L. Holappa (2015) , Occurrence of the high-speed solar wind streams over the Grand odern Maximum, The Astrophysical Journal, 801, no. 1, https://doi.org/doi:10.1088/0004-637X/801/1/30.
Namgaladze, A. A., Yu. N. Korenkov, et al. (1988) , Global model of the thermosphere–ionosphere–protonosphere system, Pure Applied Geophysics, 127, no. 2–3, p. 219–254, https://doi.org/10.1007/BF00879812.
Papitashvili, V. O., F. J. Rich (2002) , High-latitude ionospheric convection models derived from Defense Meteorological Satellite Program ion drift observations and parameterized by the interplanetary magnetic field strength and direction, Journal Geophysical Research, 107, no. A8, p. 1198, https://doi.org/10.1029/2001JA000264.
Picone, J. M., A. E. Hedin, D. P. Drob, et al. (2002) , NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues, Journal Geophysical Research, 107, no. A12, p. 1468, https://doi.org/10.1029/2002JA009430.
Qian, L., A. G. Burns, B. A. Emery, et al. (2014) , The NCAR TIE-GCM: A community model of the coupled thermosphere/ionosphere system, Modeling the Ionosphere-Thermosphere System, AGU Geophysical Monograph Ser., Vol. 201, p. 73–83, AGU, Washington, DC.
Qian, L., S. C. Solomon, et al. (2008) , Model simulations of global change in the ionosphere, Geophysical Research Letters, 35, p. L07811, https://doi.org/10.1029/2007GL033156.
Ridley, A. J., Y. Deng, G. Toth (2006) , The global ionosphere-thermosphere model, Journal Atmospheric Solar-Terrestrial Physics, 68, no. 8, p. 839–864, https://doi.org/10.1016/j.jastp.2006.01.008.
Rishbeth, H., O. K. Garriott (1969) , Introduction to Ionospheric Physics, 234 pp., Academic Press, New York.
Ruohoniemi, J. M., R. A. Greenwald (2005) , Dependencies of high latitude plasma convection: Consideration of interplanetary magnetic field, seasonal, and universal time factors in statistical patterns, Journal Geophysical Research, 110, no. A9, p. A09204, https://doi.org/10.1029/2004JA010815.
Schunk, R. W. (1996) , STEP: Handbook of Ionospheric Models, 295 pp., Utah State University, Logan, Utah.
Schunk, R. W., L. Scherliess, et al. (2004) , Global Assimilation of Ionospheric Measurements (GAIM), Radio Science, 39, p. RS1S02, https://doi.org/10.1029/2002RS002794.
Sojka, J. J. (1989) , Global scale, physical models of the $F$ region ionosphere, Review Geophysics, 27, no. 3, p. 371–403, https://doi.org/10.1029/RG027i003p00371.
Sojka, J. J., R. W. Schunk (1987) , Theoretical study of the high-latitude ionosphere's response to multicell convection patterns, Journal Geophysical Research, 92, no. A8, p. 8733–8744, https://doi.org/10.1029/JA092iA08p08733.
Sojka, J. J., R. W. Schunk, et al. (1991) , Model and observation comparison of the universal time and IMF By dependence of the ionospheric polar hole, Advances Space Research, 11, no. 10, p. 39–42, https://doi.org/10.1016/0273-1177(91)90318-E.
Sojka, J., R. Schunk, T. van Eyken, et al. (2007) , Ionospheric challenges of the International Polar Year, Eos Trans. AGU, 88, no. 15, p. 171, https://doi.org/10.1029/2007EO150003.
Themens, D. R., P. T. Jayachandran, et al. (2014) , A top to bottom evaluation of IRI 2007 within the polar cap, Journal Geophysical Research Space Physics, 119, p. 6689–6703, https://doi.org/10.1002/2014JA020052.
Themens, D. R., P. T. Jayachandran, et al. (2017) , The Empirical Canadian High Arctic Ionospheric Model (E-CHAIM): $N_mF_2$ and $h_mF_2$, Journal Geophysical Research Space Physics, 122, p. 9015–9031, https://doi.org/10.1002/2017JA024398.
Uvarov, V. M., R. Yu. Lukianova (2015) , Numerical modeling of the polar $F$ region ionosphere taking into account the solar wind conditions, Advances Space Research, 56, p. 2563–2574, https://doi.org/10.1016/j.asr.2015.10.004.
Weimer, D. R. (2005) , Improved ionospheric electrodynamic models and application to calculating Joule heating rates, Journal Geophysical Research, 110, no. A5, p. A05306, https://doi.org/10.1029/2004JA010884.
Williams, P. J. S. (1995) , A multi-antenna capability for the EISCAT Svalbard Radar, Journal Geomagnetizm Geoelectricity, 47, no. 8, p. 685–698, https://doi.org/10.5636/jgg.47.685.
Zhang, S. R., J. M. Holt, A. P. van Eyken, et al. (2010) , IPY observations of ionospheric yearly variations from high- to middle-latitude incoherent scatter radars, Journal Geophysical Research, 115, no. A3, p. A03303, https://doi.org/10.1029/2009JA014327.
Zhang, S. R., J. M. Holt, M. McCready (2007) , High latitude convection based on long-term incoherent scatter radar observations in North America, Journal Atmospheric Solar-Terrestrial Physics, 69, p. 1273–1291, https://doi.org/10.1016/j.jastp.2006.08.017.
Zhang, S.-R., J. Holt, J. Kurdzo (2011) , Millstone Hill ISR observations of upper atmospheric long-term changes: Height dependency, Journal Geophysical Research, 116, no. A2, p. A00H05, https://doi.org/10.1029/2010JA016414.
Received 17 October 2019; accepted 17 December 2019; published 7 February 2020.


Citation: Lukianova Renata , Alexander Kozlovsky (2020), Electron density in the polar F region ionosphere during solar minimum: modeling, radar and ionosonde observations, Russ. J. Earth Sci., 20, ES1004, doi:10.2205/2019ES000699.
Copyright 2020 by the Geophysical Center RAS.