RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 20, ES1006, doi:10.2205/2019ES000688, 2020
A. V. Pavlova, V. S. Arkhipkin, S. A. Myslenkov
Lomonosov Moscow State University, Faculty of Geography, Department of Oceanology, Moscow, Russia
Investigation surges is important for studying patterns of water dynamics in the Northern Caspian. Modeling of wind-surges fluctuations in the Caspian Sea was performed using the model ADCIRC (ADvanced CIRCulation). For numerical experiments was constructed an irregular triangulation computational grid that consists of 71,523 elements with minimum cell size 500 m (off the coast) and maximum – 10 km (in the center of the sea). It was compiled relative to the absolute zero water level for the Caspian Sea equal to $-28$ m BS (Baltic System), taking into account flooding and drying of the coastal land. The NCEP/CFSR reanalysis of surface wind at a height of 10 meters and the atmospheric pressure from 1979 to 2017 were used as the input data. Since the Northern Caspian is covered with ice in winter, the sea ice concentration of OSI-450 reprocessing were used. To assess the quality of the model, the obtained model level data were compared with level measurement on weather stations Tuleniy Island and Makhachkala from 2003 to 2017. The correlation coefficient for Tuleniy Island varied within 0.79–0.88, for Makhachkala – 0.67–0.79. The mean value of the root-mean-square error was about 0.11 m for Tuleniy, and 0.06 m for Makhachkala. If we exclude fluctuations in sea level with an amplitude of less than 10 cm, the correlation values increase on average by 0.04. Three main synoptic situations were identified that lead to the formation of surges of more than 1 meter on Tuleniy Island. The contribution of wind to the formation of surge height is predominant (92–100%) compared with the contribution of the horizontal pressure gradient (0–8%).
The Caspian Sea is the largest closed reservoir with its hydrological regime and climatic features located in a vast continental depression on the border of Europe and Asia. One of the features of the Caspian is the inconstancy of its level, the amplitude of which varied within 4 meters during the period of instrumental observations [Bolgov et al., 2007]. Most researchers explain this phenomenon by changes in climatic conditions on which overlap anthropogenic factors.
Almost the entire coast of the shallow Northern Caspian is subject to the influence of non-periodic anemobaric-surges oscillation level [Baidin and Kosarev, 1986]. They are mainly generated by the action of the tangential wind stress, but also to a lesser extent as a result of changes in atmospheric pressure [Terziev et al., 1992]. In addition to the main factors, the magnitude of fluctuations is influenced by the depth of the sea, the slopes and bottom topography, the configuration of the coastline, the presence of aquatic vegetation, the ice regime and the amount of runoff [Nesterov, 2016].
Studies of surges in the Caspian Sea have a long history. Quite often, the authors limited themselves to summarizing the results by observation level posts. [Apollov, 1935; Fomina, 1967]. So, A. I. Karakash developed a method according to the level post of Makhachkala [Karakash, 1939]. It establishes the relationship between changes in sea level, atmospheric pressure and wind speed over a certain period of time. However, this technique takes place only with a gradual change in pressure and sea level. S. I. Kan admitted that when forecasting the level, the effect of the wind can be replaced by atmospheric pressure gradients [Kan, 1958]. V. Kh. German and N. P. Dovgopol, analyzed the components of the maximum levels of the Caspian Sea for different periods of the level dynamics. They proposed to apply the asymptotic law of the extreme members of the sample (asymptotic law of distribution of prime numbers) to calculate the maximum sea level increments, which was developed by E. I. Gumbel [German and Dovgopol, 1967; Gumbel, 1965]. N. A. Skriptunov and N. D. Gershtansky were engaged in research of wind surge phenomena on the Volga seaside [Gershtansky, 1973; Skriptunov, 1958].
In the Laboratory of Marine Applied Research of the Hydrometeorological Center of Russia, has been developed and operates within the framework of operational technology a method of hydrodynamic prediction of sea level and currents in the Caspian Sea [Nesterov et al., 2018; Verbitskaya et al., 2002; Zil'bershtein et al., 2001]. Forecasts are made using a rectangular computational grid.
In recent decades, a lot of level posts have been closed. Due to the limited number of posts in space and a large step of observation of the level, it is not possible to trace in detail the formation of surge events. Thus, the method of mathematical modeling is used for a more detailed analysis of the spatial-temporal variability.
The aim of the work is to identify patterns of formation wind-surges fluctuations in the Northern Caspian based on the technology of mathematical modeling for the period from 1979 to 2017 using the ADCIRC (ADvanced CIRCulation) model. The verification of the model was carried out on the basis of a comparison of the obtained results with observational data. It is necessary to assess the influence of individual factors, as well as to compare individual simulation results with field data.
Modeling of wind-surges fluctuations in the Caspian Sea was performed using the model ADCIRC. The model is developed and maintained by a combination of partners [Luettich et al., 1992], (Luettich, R. A., Westerink J. J. (2004), Formulation and numerical implementation of the 2D/3D ADCIRC finite element model version 44.XX. Available at https://adcirc.org/files/2018/11/2004_Luettich. pdf). ADCIRC is a numerical model for calculating water circulation and sea level fluctuations that solve the complete equations of motion for a moving fluid on a rotating earth. Typical ADCIRC applications include the following tasks: prediction of storm surges and floods, modeling tides and wind driven circulation, near shore marine operations, dredging feasibility and material disposal studies.
The model equations have been formulated using the hydrostatic pressure and Boussinesq approximations. It uses a finite element method for discretization by spatial variables, which allows the use the unstructured grids. The approximation in time is carried out by the finite difference method. It takes into account such parameters as Coriolis force, atmospheric pressure, wind stress, tidal potential and bottom friction. In the model, you can set the properties of the underlying surface. ADCIRC also includes flooding and drying of low-lying areas, as well as river flow.
There are two options for using the ADCIRC model: as a two-dimensional depth integrated model (2DDI), and as a three-dimensional model (3D). In this work, we used a two-dimensional model. Exceeding the level is obtained by solving the depth-integrated continuity equation in Generalized Wave-Continuity Equation form (GWCE) [Westerink et al., 1994]. Velocity obtained from the solutions of momentum equations. All non-linear terms are preserved. The ADCIRC architecture successfully allows to use this model complex in parallel computing. ADCIRC can be run with either a Cartesian or a spherical coordinate system. The initial equations of the 2DDI ADCIRC model are:
\begin{eqnarray*} \frac{\partial U}{\partial t} + U \frac{\partial U}{\partial x} + V \frac{\partial U}{\partial y} - fV = \end{eqnarray*} \begin{equation} \tag*{(1)} - g \frac{\partial}{\partial x} \left[ \eta + \frac{P_a}{g \rho_0} \right] + \frac{\tau_{sx} -\tau_{bx}}{\rho_0 H} + \frac{M_x-D_x}{H} \end{equation}\begin{eqnarray*} \frac{\partial V}{\partial t} + U \frac{\partial V}{\partial x} + V \frac{\partial V}{\partial y} - fV = \end{eqnarray*} \begin{equation} \tag*{(2)} - g \frac{\partial}{\partial y} \left[ \eta + \frac{P_a}{g \rho_0} \right] + \frac{\tau_{sy} -\tau_{by}}{\rho_0 H} + \frac{M_y-D_y}{H} \end{equation}
\begin{equation} \tag*{(3)} \frac{\partial^2 \eta}{\partial^2 t} + \tau_0 \frac{\partial \eta}{\partial t} + \frac{\partial J_x}{\partial x} + \frac{\partial J_y}{\partial y} =0 \end{equation}
\begin{eqnarray*} J_x = - Q_x \frac{\partial U}{\partial x} - Q_y \frac{\partial U}{\partial y} + f Q_y - \end{eqnarray*} \begin{eqnarray*} \frac{g}{2} \frac{\partial \eta^2}{\partial x} - \frac{H}{\rho_0} \frac{\partial P_a}{\partial x} + \frac{\tau_{sx} - \tau_{bx}}{\rho_0} + \end{eqnarray*} \begin{equation} \tag*{(4)} (M_x - D_x ) + \tau_0 Q_x + U \frac{\partial \eta}{\partial t} -gH \frac{\partial \eta}{\partial x} \end{equation}
\begin{eqnarray*} J_y = - Q_x \frac{\partial V}{\partial x} - Q_y \frac{\partial V}{\partial y} - f Q_x - \end{eqnarray*} \begin{eqnarray*} \frac{g}{2} \frac{\partial \eta^2}{\partial y} - \frac{H}{\rho_0} \frac{\partial P_a}{\partial y} + \frac{\tau_{sy} - \tau_{by}}{\rho_0} + \end{eqnarray*} \begin{equation} \tag*{(5)} (M_y - D_y ) + \tau_0 Q_y + V \frac{\partial \eta}{\partial t} -gH \frac{\partial \eta}{\partial y} \end{equation}
\begin{eqnarray*} \quad \tau_{sx} = \tau_{sx,\mathrm{wind}} + \tau_{sx,\mathrm{wave}} \end{eqnarray*} \begin{equation} \tag*{(6)} \tau_{sy} = \tau_{sy,\mathrm{wind}} + \tau_{sy,\mathrm{wave}} \end{equation}
The terms in (1)–(6) are the following – $x$, $y$ and $t$ are horizontal grid points and time; $H = h + \eta$ is total water depth; $\eta$ is surface elevation; $h$ is bathymetric depth; $U$ and $V$ are depth-integration currents in the $x$- and $y$-directions, respectively; $Q_x = UH$ and $Q_y = VH$ are fluxes per unit width; $f$ is the Coriolis parameter; $g$ is gravitational acceleration; $P_a$ is atmospheric pressure at the surface; $\rho_0$ is the reference density of water; ($\tau_{sx,\mathrm{wind}}, \tau_{sy,\mathrm{wind}}$) and ($\tau_{sx,\mathrm{wave}}, \tau_{sy,\mathrm{wave}}$) are surface stresses due to winds and waves, respectively; $\tau_{bx}$ and $\tau_{by}$ are bottom stresses; $M_x$ and $M_y$ are horizontal eddy viscosity; $D_x$ and $D_y$ are momentum dispersion terms; $\tau_0$ is a numerical parameter that optimizes the phase propagation properties.
This model has already been successfully used to simulate surges in the White and Barents Sea [Korablina et al., 2017], as well as in the Sea of Okhotsk [Ivanova et al., 2015].
 |
| Figure 1 |
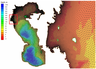
Using the Aquaveo Surface-water Modeling System (SMS 11.0) application, maps were digitized and an irregular triangulation computational grid was constructed (Figure 1). The grid is constructed depending on the number of points on the coastline and consists of 71,523 elements. The minimum cell size was 500 m (off the coast), the maximum – 10 km (in the center of the sea). To create a digital elevation model, marine navigational maps of $1:25,000$, $1:100,000$, $1:750,000$ scale were used. The computational grid was compiled relative to the water level for the Caspian Sea at 28 meters below sea level, taking into account flooding and drying of the coastal land. The use of irregular grid seems to be perspective for computing coastal processes and more accurate representation of small islands.
As the input data were used the fields of surface wind (at a height of 10 meters) and the atmospheric pressure of the NCEP (National Centers for Environmental Prediction) CFSR (Climate Forecast System Reanalysis) reanalysis. The NCEP/CFSR reanalysis is a modern product of the National Centers for Environmental Prediction, implemented in 2010. The CFSR is a global atmosphere–ocean–land–sea ice system with high resolution that provides the best estimate of the state of these interconnected systems. Data covering the period from 1979 to 2010 have a 1-hour time interval and a spatial resolution of $\sim 0.3\mbox{°} \times 0.3\mbox{°}$ [Saha et al., 2010]. For numerical calculations from 2011 to 2017, the NCEP/CFSv2 version (Climate Forecast System Version 2) reanalysis was used, having a spatial resolution of $\sim 0.2\mbox{°} \times 0.2\mbox{°}$ [Saha et al., 2014]. Also, sea ice concentration was set as input (OSI-450), which is reprocessing the brightness temperature data based on passive microwave radiometer SMMR, SSM/I and SSMIS and ECMWF ERA-Interim reanalysis (EUMETSAT Ocean and Sea Ice Satellite Application Facility. Global sea ice concentration climate data record 1979–2015 (v2.0, 2017), [Online]. Norwegian and Danish Meteorological Institutes. http://osisaf.met.no/docs/osisaf_cdop3_ss2_ pum_sea-ice-conc-climate-data-record_v2p0.pdf). The data covers the period from 1979 to 2017 with a daily interval and a spatial resolution of $\sim 0.2\mbox{°} \times 0.2\mbox{°}$. Data output occurs every hour.
 |
| Figure 2 |
To assess the quality of the model, the obtained model level data were compared with level measurement on weather stations Tuleniy Island and Makhachkala (with time step of 6 hour) from 2003 to 2017 (Figure 2). Comparison was carried out after the removal of low-frequency fluctuations of the sea level (periods longer than 30 days). Due to the presence of gaps in field observations, digital filters could not be used to remove these fluctuations. To solve this problem, polynomials of the seventh order were computed, using Chebyshev coefficients. Then a hypothesis about the equality of variances was tested, based on the $F$-distribution.
 |
| Table 1 |
 |
| Table 2 |
A statistical sea level analysis was conducted for Tuleniy Island for the period from 2003 to 2017 (Table 1) and Makhachkala from 2003 to 2011 (Table 2). The correlation coefficient (comparison of model and field data) for Tuleniy varied within 0.79–0.88, for Makhachkala – 0.67–0.79. The mean value of the root-mean-square error was about 0.11 m for Tuleniy, and 0.06 m for Makhachkala. If we exclude fluctuations in sea level with an amplitude of less than 10 cm, the correlation values increase on average by 0.04. For example, in 2007, the correlation value is 0.86, and excluding fluctuations is 0.91. These results make it possible to say that, firstly, the model adequately describes the obtained level change data, and secondly, ADCIRC reproduces surges very well.
Three main synoptic situations were identified that lead to the formation of surges of more than 1 meter on Tuleniy Island:
 |
| Figure 3 |
To estimate the contribution of wind stress and atmospheric pressure to the formation of set up and set down sea level, separate experiments were conducted only with wind and atmospheric pressure and only with wind. In both cases, ice was also counted. It was revealed that the wind contribution to the formation of surge height is predominant (92–100%) compared with the contribution of the horizontal pressure gradient (0–8%) in different synoptic situations (Figure 3). A positive contribution means that the level has increased due to pressure, and vice versa.
 |
| Figure 4 |
From 1979 to 2008 there is a long-term tendency to reduce the number of cases of formation wind-surges level fluctuations (Figure 4). Since 2008, the opposite trend has been observed. This tendency is valid not only for all fluctuations with an amplitude of more than 0.5 m, but also for 0.2, 0.4, 0.6 and 0.8 m. During the year at the Tuleniy Island, both the number and the height of set down water level more than set up.
The largest in magnitude, wind-surges level fluctuations at the Tuleniy were observed in February 1981 – the level set down was 1.8 m, and the level set up was 1.5 m.
 |
| Figure 5 |
 |
| Figure 6 |
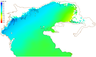
A surge analysis was conducted on 19–23 November 2013 (Figure 5 and Figure 6). During this period, an anticyclone was formed, which moved eastward over the Northern Caspian. At the same time, a cyclone was formed over Europe. On 19 November the north wind was observed, which on 20 November changed its direction to the south-east, and on the 23rd to the east. Wind speed reached 15 m/s.
Figure 5 shows the time course of the sea level at Tuleniy. Results indicate very good agreement between the model and instrumental data, where the maximum sea level was 1 m. The pressure contribution reached 5%.
Figure 6 shows the spatial distribution of the calculated sea level in the northern part of the Caspian Sea at 12 a.m. on 21 November 2013. The maximum values of the level at the northwestern coast reached 2.5 m. In the east coast there was a decrease in sea level of up to 1 m. The simulated flooded area was 15 km.
 |
| Figure 7 |
 |
| Figure 8 |
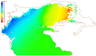
Also, an analysis was conducted to surge conditions from 27 March to 1 April 2015 (Figure 7 and Figure 8). During this period, a strong anticyclone was formed north of the Caspian Sea, and an area of low pressure over Europe. The east wind was predominantly observed at speeds up to 17 m/s.
Figure 7 shows the time course of the sea level at Tuleniy, where there is a good agreement between the model and instrumental data. The sea level at the station reached 1.3 m. During the surge, two peaks were modeled. At the first peak, a negative pressure contribution of up to 1% was observed, and at the second, a positive contribution of up to 1.5%.
Figure 8 shows the spatial distribution of the calculated sea level in the northern part of the Caspian Sea at 12 a.m. on 30 March 2015. The maximum values of the surge at the western coast reached 3 m. Along the eastern coast, the sea level has decreased to 3 m. The area that was flooded as a result of modeling was 15 km.
 |
| Figure 9 |
 |
| Figure 10 |
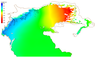
The surge analysis was carried out for the conditions of the storm 12–16 March 1995, which had the most disastrous consequences after the surge in 1952 (Figure 9 and Figure 10).
During the surge, there was a sharp increase in horizontal pressure gradients over the North Caspian due to the displacement of the strong anticyclone from the north and the deepening of the cyclone over the Black Sea. In the northern part of the Caspian Sea, there was a strong east-northeast (12–13 March) and east (from 14 March) winds with speeds of up to 20 m/s. During the storm, a current with a general direction to the west-south-west with speeds up to 1 m/s was formed.
On 15 March wind intensification was observed, due to which two peaks were formed in sea level at Tuleniy (Figure 9). The maximum sea level at the station was 1.3 m. There was a negative pressure contribution of up to 8%.
The duration of the wind in conjunction with large pressure gradients and direction of currents caused a catastrophic surge, the maximum values of which reached 2 m on the northwestern coast of the North Caspian. At the same time, a catastrophic sea level decline of up to 4.5 m was observed on the east coast. The simulated land flood bandwidth reaches 25 km.
The effect of ice conditions should be considered in each case separately. Due to different meteorological conditions and ice concentration, different responses can be observed. In most cases, the presence of ice leads to a decrease in sea level fluctuations.
Verification of the ADCIRC model, implemented on the original irregular grid, covering the entire Caspian Sea, showed that the level fluctuations calculated using the ADCIRC model reliably describe the observed level changes in space and time. The use of a triangulation grid made it possible to increase the density of nodes in the coastal zone of the Northern Caspian with a minimum step of 500 m, which leads to a more accurate description of the wind-surges fluctuations.
The developed method for isolating surges by eliminating long-period oscillations (a period of more than 35–40 days) from the general sea level made it possible to calculate the statistical characteristics of surges for a long period from 1979 to 2017 in the studied area.
Several basic synoptic situations have been identified, in which surges of more than 1 meter form along the western coast of the Northern Caspian. During the year, both the number and the height of water level set down at Tuleniy are more than surges.
The long-term tendency to reduce the number of cases of formation wind-surge oscillations from 1979 to 2008 is noted. Since 2008, the opposite trend has been observed.
The contribution of wind to the formation of surge height is predominant compared with the contribution of the horizontal pressure gradient.
Apollov, B. A. (1935) , The water balance of the Caspian Sea and possible changes in it, Proceedings of the Central Institute of Experimental Hydrology and Meteorology, 44, no. 2, p. 11–18 (in Russian).
Baidin, S. S., A. N. Kosarev (Eds.) (1986) , The Caspian Sea: Hydrology and Hydrochemistry, 261 pp., Nauka, Moscow (in Russian).
Bolgov, M. V., G. F. Krasnozhon, A. A. Lyubushin (2007) , The Caspian Sea: Extreme Hydrological Events, 381 pp., Nauka, Moscow (in Russian).
Fomina, N. D. (1967) , About non-periodic fluctuations of the level in the Apsheron archipelago, Proceedings of the Scientific and Technical Conference on the Hydrometeorological Services of Azerbaijan and the Caspian Sea, Baku, p. 38–40, Hydrometeorological Services of Azerbaijan, Baku (in Russian).
German, V. X., N. P. Dovgopol (1967) , The calculation of the maximum levels of low supply on the example of the Caspian and Aral seas, SOI Proceedings, no. 80, p. 17–29 (in Russian).
Gershtansky, N. D. (1973) , Properties of wind-surges water level fluctuations in the wellhead seashore of Volga, SOI Proceedings, no. 116, p. 131–145 (in Russian).
Gumbel, E. (1965) , Statistics of Extreme Values, 465 pp., Mir, Moscow (in Russian).
Ivanova, A. A., V. S. Arkhipkin, S. A. Myslenkov, et al. (2015) , Modeling of storm surges in the coastal zone of the Sakhalin Island, Moscow University Bulletin, Series 5, Geography, no. 3, p. 41–49 (in Russian).
Kan, S. I. (1958) , Long period forecasts of ice phenomena on the Caspian Sea, Proceedings of the Central Institute of forecasts, no. 76, p. 64–70 (in Russian).
Karakash, A. I. (1939) , Method of predicting short-term changes in the level in the internal seas of the USSR, Meteorology and Hydrology, no. 3, p. 78–82 (in Russian).
Korablina, A. D., A. T. Kondrin, V. S. Arkhipkin (2017) , Simulation of surges in the White and Barents seas for the period 1979–2015, Proceedings of the Hydrometcentre of Russia, no. 364, p. 144–158 (in Russian).
Luettich, R. A., J. J. Westerink, N. W. Scheffner (1992) , ADCIRC: an advanced three-dimensional circulation model for shelves coasts and estuaries, Report 1: Theory and methodology of ADCIRC-2DDI and ADCIRC-3DL, Dredging Research Program Technical Report DRP-92-6, U.S. Army Engineers Waterways Experiment Station, Vicksburg, MS.
Nesterov, E. S. (Ed.) (2016) , Water balance and level fluctuations of the Caspian Sea. Modeling and prediction, 378 pp., Triada LTD, Moscow (in Russian).
Nesterov, E. S., S. K. Popov, A. L. Lobov (2018) , Statistical characteristics and modeling of storm surges in the North Caspian Sea, Russian Meteorology and Hydrology, 43, no. 10, p. 664–669, https://doi.org/10.3103/S1068373918100059.
Saha, S., et al. (2010) , The NCEP Climate Forecast System Reanalysis, Bulletin of American Meteorological Society, 91, p. 1015–1057.
Saha, S., et al. (2014) , The NCEP Climate Forecast System Version 2, Journal of Climate, 27, no. 6, p. 2185–2208, https://doi.org/10.1175/JCLI-D-12-00823.1.
Skriptunov, N. A. (1958) , Hydrology of the pre-mouth Volga coastal waters, 143 pp., Gidrometeoizdat, Moscow (in Russian).
Terziev, F. S., A. N. Kosarev, A. A. Kerimov (Eds.) (1992) , Hydrometeorology and hydrochemistry of seas. Vol. VI. The Caspian Sea. Issue 1. Hydrometeorological conditions, 131–145 pp., Gidrometeoizdat, St. Petersburg (in Russian).
Verbitskaya, O. A., O. I. Zilberstein, S. K. Popov, et al. (2002) , Method of short-term hydrodynamic forecasting of storm surges in the north part of the Caspian Sea and results its testing, Informational Collection, no. 29, p. 76–89 (in Russian).
Westerink, J. J., C. A. Blain, R. A. Luettich, et al. (1994) , ADCIRC: an advanced three-dimensional circulation model for shelves coasts and estuaries, Report 2: Users manual for ADCIRC-2DDI. Dredging Research Program Technical Report DRP-92-6, U.S. Army Engineers Waterways Experiment Station, Vicksburg, MS.
Zil'bershtein, O. I., S. K. Popov, M. M. Chumakov, et al. (2001) , A Procedure for Calculating Extreme Characteristics of the Northern Caspian Sea Level, Water Resources, 28, no. 6, p. 632–639, https://doi.org/10.1023/A:1012833712510.
Received 14 May 2019; accepted 29 October 2019; published 6 February 2020.


Citation: Pavlova A. V., V. S. Arkhipkin, S. A. Myslenkov (2020), Storm surge modeling in the Caspian Sea using an unstructured grid, Russ. J. Earth Sci., 20, ES1006, doi:10.2205/2019ES000688.
Copyright 2020 by the Geophysical Center RAS.