RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 19, ES6010, doi:10.2205/2019ES000697, 2019
A. A. Lushnikov1, Sh. R. Bogoutdinov1,2
1Geophysical Center of the Russian Academy of Sciences (GC RAS), Moscow, Russia
2Schmidt Institute of Physics of the Earth of the Russian Academy of Sciences (IPE RAS), Moscow, Russia
This paper reviews the methods of treating the results of geophysical observations typically met in various geophysical studies. The main emphasize is given to the sets of data on the phenomena undergone the actions of random factors. These data are normally described by the distributions depending on the nature of the processes. Among them the magnitude of earthquakes, the diameters of moon craters, the intensity of solar flares, population of cities, size of aerosol and hydrosol particles, eddies in turbulent water, the strengths of tornadoes and hurricanes and many other things. Irrespective of the causes for their randomness these manifestations of planetary activity are characterized by few distribution functions like Gauss distribution, lognormal distribution, gamma distribution, and algebraic distributions. Each of these distributions contains empirical parameters the values of which depend on the concrete nature of the process. Especially interesting are so called "thick" distributions with the algebraic tails. Possible parametrizations of these distributions are discussed.
The random factors playing the central role in various geophysical processes insistently demand the application of stochastic approaches for their study. This is true even for phenomena describing by well based equations, because interactions between several nonlinear processes often lead to their chaotic behavior. The approaches allowing for consideration such processes had appeared since very long ago and have proven their use in all cases without exception [Ding and Li, 2007; Eckmann and Ruelle, 1985; Van Kampen, 2007; Klyatskin, 2005; McKibben, 2011; Michael, 2012].
In this paper we discuss the geophysical phenomena describing by slowly varying functions of time over significant time intervals rather than short-period fluctuations, which are in addition small (in amplitude, for example) and from the first sight cannot noticeably affect the course of the geophysical events. The most bright example of such phenomena is well known in the rock destruction theory, when very small and almost imperceptible changes accumulate, and ultimately lead to disruptions in the development of rock material and then to complete disruption of the rock [Eckmann and Ruelle, 1985; Michael, 2012]. Among other geophysical phenomena it is necessary to mention one remarkable mechanism of occurrence of earthquakes. Individual oscillations of the plates can be small and considered in the harmonic approximation. However, the interactions between the individual modes can lead to their merger in such a way that the energies of individual modes are added and a principally new mode forms, which is yet described in the harmonic approximation, but it has the energy equal to the sum of the energies of the merged oscillations. This merger process continues until a single wave of very large amplitude is generated. Its energy continues to grow due to the capture of low-energy modes, which leads to a catastrophe (an earthquake, for example). Similar mechanism can also be responsible for the formation of giant sea waves referred often to as the killer waves. The dynamics of these accumulation processes depends strongly on the distributions of the energy carriers [Bailey, 1964; Eckmann and Ruelle, 1985; Mazo, 2002; McKibben, 2011; Michael, 2012].
Another example is the atmospheric aerosol and its role as the climate formation factor [Adams and Seinfeld, 2002; Barrett and Clement, 1991; Janson et al., 2001; Seinfeld and Pandis, 1998].
Generally accepted evolutionary equations more or less correctly describe the {\em average} temporal evolution of complex geophysical structures (changes in the state of the atmosphere, aerosol processes and climate, the development of territorial structures, demographic structures, etc) once the transition rates between states of the system are known. For example, the simplest balance equation with empirically introduced birth and death rates describe the dynamics of transitions between the states with different population sizes. If, however, we introduce the random factor that spreads the values of the birth and death rates, the dynamic picture can radically change.
Geophysical data are represented by numerical arrays of dimension $\Omega$. For example, one-dimensional arrays can represent data on concentrations of harmful emissions in the atmosphere or a sequence of radar signals from a satellite at predetermined time intervals, or, for example, randomly selected measurement times. Our idea is that there is a certain probabilistic process behind geophysical data. Each data sequence is implemented with some probability. There are several ways to process a signal. This can be, for example, Fourier or wavelet analysis, which allows one to select the main frequencies of the signal. With this approach, it is assumed that the signal itself is deterministic, and what we observe is a noise + signal. Our task is to try to clear the signal from the hindrances. This is precisely the problem that always arises in a location (sound, radio), when the emitted signal is known, whereas the incoming signal is composed of noise plus the reflected (partially or completely) signal, by which we should judge on the geophysical processes occurring far away from the receiver. This is how objects are located by modern positioning systems. The noise introduces an error for reducing which it is necessary to establish the nature of the noise. In the case of satellite sensing, several such reasons have been established: we have elucidated the role of Rydberg complexes formed at altitudes of 70 - 110 km in the ionosphere and the role of aerosol particles exposed to solar radiation, which leads to their charging. The strong influence of these particles on the state of the ionospheric plasma is beyond any doubt [Golubkov et al., 2010; 2014].
Next, there is another type of geophysical signals when the characteristics of the signal generator are not known, and the task of processing is to extract the maximum information from the signal. For example, it may be a signal from extraterrestrial civilizations. Then we can expect to find a dominant signal in it and try to filter it out. It is possible to imagine another situation where the signal does not contain a dominant at all. Attempts to apply some averaging procedures to irregular signal turn out completely unsuccessful [Bailey, 1964; Mazo, 2002]. As an example, the noises from ther Universe can be mentioned. The question is, then what to do with such signals?
Our probabilistic concept assumes that a stochastic signal is described by the probability of its implementation. For definiteness, we consider a stationary signal with a random amplitude and introduce a probability to find the given amplitude in the signal. Our task is to find this probability from the measurement data, which are represented by a set of points belonging to signals in a given amplitude interval. As the interval narrows and the measurement time lengthens, such a procedure allows one to calculate the density of the distribution of measurements. However, due to lack of data (and often measurement time), this procedure is low productive. Therefore, it is more progressive to use cumulative distributions, i.e., to calculate the number of measurements with an amplitude above a given one. Now, to calculate the distribution density, a discrete mathematical analysis apparatus is required, since we will have to differentiate a function defined on a discrete set.
As an example, we consider an aerosol counter that determines the concentration of dispersed impurities in atmospheric air [Julanov et al., 1983; Zagaynov et al., 1989]. In this counter, each particle enters a countable volume illuminated by a laser beam. The signal scattered from the beam is read by the photomultiplier. This counter can determine the concentration of particles, provided that the speed of pumping air through the counting volume is known, and the particles fall into the counting volume one at a time. But a single count cannot be guaranteed, particles in the counting volume can fall in two, three, etc. This means that the counter will underestimate the counted concentration of particles. Now the signal (response from the samples) will have a different amplitude depending on the number of particles falling into the counting volume . Thus, a typical task arises of analyzing a stochastic signal. This task is complicated by the fact that the aerosol impurity may contain particles of different sizes (polydisperse aerosol). Then the problem of analysis is complicated, but still possible (see refs [Adams and Seinfeld, 2002; Barrett and Clement, 1991; Julanov et al., 1984; 1986; Janson et al., 2001; Leyvraz, 2003; Lushnikov and Kagan, 2016; Seinfeld and Pandis, 1998; Schmeltzer et al., 1999]
In what follows we will use the examples adopted from the physics of dispersed particles. We consider the systems comprising the set of particles of different sizes and will explain the basic idea of the stochastic approach.
The particle size distributions play the central role in physics and chemistry of atmospheric aerosol, although a direct observation of the distributions are possible only in principle. Practically what we really measure is just a response of an instrument to a given particle size distribution,
\begin{equation} \tag*{(1)} P(x)=\int R(x,a)f(a)da \end{equation}Here $f(a)$ is the particle size distribution (normally $a$ is the particle radius), $P(x)$ is the reading of the instrument measuring the property of aerosol $x$, and $R(x,a)$ is referred to as the linear response function of the instrument. For example, $P(x)$ can be the optical signal from an aerosol particle in the sensing volume of an optical particle counter, the penetration of the aerosol through the diffusion battery (in this case $x$ is the length of the battery), or something else. The function $f(a)$ cannot depend on the dimensional variable $a$ alone. The particle size is measured in some natural units $a_s$. In this case the distribution is a function of $a/a_s$ and depends on some other dimensionless parameters or groups. The particle size distribution is normalized as follows:
\begin{equation} \tag*{(2)} \int\limits_0^\infty f(a/a_s)\frac{da}{a_s}=1. \end{equation}The length $a_s$ is a parameter of a distribution. Although the aerosol particle size distribution is so elusive characteristic of the aerosol, it is still convenient to introduce it because all properties of aerosols can be unified in this way.
In some cases the distribution function can be found theoretically on solving dynamic equations governing the time evolution of the particle size distribution, but the methods for analyzing these equations are not yet reliable, not mentioning the information on the coefficients entering them. This is the reason why the phenomenological distributions are so widely spread.
In various geophysical problems it is principally impossible to exclude the influence of random factors. This means that we have to operate with the probability of finding the system in a given state, rather than average time (or ensemble) characteristics of the state. Meanwhile, ordinary considerations always ignore the deviations from the average picture and operate only with the average characteristics or lower moments. This fact means that it is necessary to elaborate the efficient methods for consideration of random processes in geophysical systems. For example, global disasters such as earthquakes, tsunamis, tornadoes, epidemics, environmental disasters, etc. result from a coherent interplay of random factors. In such cases, the mathematical description should rely upon other principles than those widely adopted in modern geophysics. Specifically, we refuse of the description of the state of the system in terms of time dependent average distributions and apply the description in terms of the occupation numbers. We exemplify our idea by considering the set of particles of different size.
\begin{eqnarray*} Q=n_1,n_2\ldots n_g\ldots \end{eqnarray*}The set changes through time $t$. For applications however it is enough to have the average spectrum,
\begin{eqnarray*} \bar n_g(t)=\sum\limits_{n_g}n_g(Q)W(Q,t)\Delta(n_g-n_g(Q)) \end{eqnarray*}where $W(n_1,n_2\ldots)$ is the probability of realization of the given set, $n_g(Q)$ denotes the number of the $g$–objects in the realization $Q$, $\Delta$ stands for the Kroneker delta symbol. Of course, it is much more convenient to deal with the average spectrum depending on one variable. The problem is then from where to get the probability $W(Q,t)$?
The dynamics of the system depends on the rates of transitions between the states $Q$. Let us assume that these rates are known and that they depend on the couple of the states $Q^+$ and $Q$. The development of the system is then given by the time sequence
\begin{eqnarray*} Q^+\to Q\to Q^{-}, \end{eqnarray*}i.e., the system jumps from the point of the phase space $Q^+$ to point $Q$, the to $Q^-$ etc. It is possible to write down the equation (the Master equation) governing the the time evolution of the probability $W(Q,t)$.
\begin{equation} \tag*{(3)} \begin{array}{rl} \frac{\partial W(Q,t)}{\partial t}=&\sum\limits_{Q^+}A(Q^+,Q)W(Q^+,t)- &W(Q,t)\sum\limits_{Q^-}A(Q,Q^-) \end{array} \end{equation}The first term on the right–hand side of this equation is just the rate of transitions from all possible states $Q^+$ to the state $Q$, the second term is responsible for the losses of the probability because of the jumps to all accessible states $Q^-$.
We demonstrate first the ideology of the mean field approach, The simplest example is the point moving along $x$ axis with the velocity $v(t)$. Let the average velocity be $\bar v$ and otherwise the function $v(t)$ is random. Then the natural desire comes up to write the equation of motion in the form,
\begin{eqnarray*} \frac{d\bar x}{dt}=\bar v \end{eqnarray*}and to solve it,
\begin{eqnarray*} \bar x(t)=\bar vt \end{eqnarray*}The result can be compared to the exact solution,
\begin{eqnarray*} x(t)=\int\limits_0^tv(t')dt' \end{eqnarray*}It is clear that the average $\bar x$ can deviate from exact solution very strongly.
Another example operates with the birth-death process. We consider the evolution of the total size $n(t)$ of population in a town. Let us introduce birth and death rates ($\alpha$ and $\beta$ respectively). Then for the average size $\bar n(t)$ we can write the equation,
\begin{eqnarray*} \frac{d\bar n}{dt}=\alpha\bar n-\beta\bar n. \end{eqnarray*}The solution to this equation is well known,
\begin{eqnarray*} \bar n(t)=\bar n_0e^{\mu t}, \end{eqnarray*}where $\mu=\alpha-\beta$ is the difference between fertility and mortality. If $\mu>0$ the population grows, otherwise ($\mu<0$) it diminishes. At $\mu=0$ the population does not change and remain equal to $n_0$ – its initial size.
Now let us introduce a random factor. We assume that $\mu$ is distributed over the Gauss low,
\begin{eqnarray*} W(\mu)=\sqrt{\frac a\pi}e^{-a\mu^2} \end{eqnarray*}Here $a$ is a constant. Let us calculate the average size,
\begin{equation} \tag*{(4)} \bar n(t)=n_0\sqrt{\frac a\pi}\int\limits_{-\infty}^\infty e^{-a\mu^2+\mu t}d\mu \end{equation}On integrating over $\mu$ yields,
\begin{eqnarray*} \bar n(t)=\exp(t^2/2\sqrt a) \end{eqnarray*}We see that the random factor decisively changes the result. The population grows even if the mortality exceeds the fertility.
Our next example is a particle jumping over 1D lattice. The probability per unit time for a jump between neighboring sites is $1/\tau$. Then according to our ideology we can write,
\begin{eqnarray*} \frac{dW}{dt}=\frac1\tau(W_{n-1}-W_n) \end{eqnarray*}where $\tau$ has the meaning of average time of a single jump. The Laplace transform $w_n(p)=\int_0^\infty W_n(t)e^{-pt}$ is determined by the set of algebraic equations,
\begin{equation} \tag*{(5)} pw_n-W_n(0)=\frac1\tau(w_{n-1}-w_n) \end{equation}where $W_n(0)$ is the initial probability for the particle to occur at the site $n$. We assume that $W_n(0)=\delta_{n,0}$, i.e., the particle is initially located at the origin of coordinate. The set Eq. (5) is then readily solved,
\begin{eqnarray*} w_n(p)=(p+1/\tau)^n \end{eqnarray*}On inverting this we find,
\begin{eqnarray*} W_n(t)=\frac{(t/\tau)^n}{n!}e^{-t/\tau} \end{eqnarray*}This is the Poisson distribution that emerges instead of $W_n(t)=\Delta(n-n_0(t))$. Here $n_0(t)1/\tau$ is the average velocity of the particle and $\Delta(i-k)$ stands for the Kroneker delta ($\Delta(0)=1$ and $\Delta(x)=0$ at $x\neq0$).
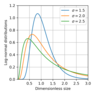
The lognormal distribution looks as follows,
\begin{equation} \tag*{(6)} f_L(a)=\frac1{\sqrt{2\pi} (a/a_s)\ln\sigma}\exp\left[-\frac1{2\ln^2\sigma}\ln^2\frac a{a_s}\right] \end{equation} |
| Figure 1 |
Here $a$ is the particle radius. This distribution depends on two parameters: $a_s$ and $\sigma$, where $ a_s$ is the characteristic particle radius and $\sigma$ ($\sigma>1$) is the width of the distribution. Equation (6) is known as the lognormal distribution. It is important to emphasize that it is not derived from theoretical considerations. Rather, it is introduced by hands. The function $f_L(a)$ is shown in Figure 1 for different $\sigma$.
This size distribution is given by the formula:
\begin{eqnarray*} f_G(a)=\left(\frac a{a_s}\right)^k\frac j{\Gamma((k+1)/j)}\exp[-(a/a_s)^j] \end{eqnarray*} |
| Figure 2 |
Here $\Gamma(x)$ is the Euler gamma–function. The distribution $f_G$ depends on three parameters, $r_s$, $k$ and $j$. Figure 2 displays the generalized gamma-distribution for three sets of its parameters.
Once the particle size distributions are known, it is easy to derive the distribution over the values depending only on the particle size;
\begin{eqnarray*} f(\psi_0)=\int\delta(\psi_0-\psi(a))f(a)\frac{da}{a_s} \end{eqnarray*}Here $\delta(x)$ is the Dirac delta function. For example, if we wish to derive the distribution over the particle masses, then $\psi(a)=(4\pi a^3/3)\rho$ , where $\rho$ is the density of the particle material. Of course, the properties of aerosols depend not only on their size distributions. The shape of aerosol particles and their composition are important factors.
Lognormal distribution often applies in approximate calculations of important particle formation processes like condensation and coagulation [Barrett and Clement, 1991; Friedlander, 2000; Janson et al., 2001; Seinfeld and Pandis, 1998].
The distribution $f_\lambda(x)$ possessing the property
\begin{eqnarray*} f_\lambda(ax)=a^\lambda f_\lambda(x) \end{eqnarray*}is referred to as the scaling invariant one. The reasons for this are apparent: if we change the scale of $f$ then the distribution preserves its shape but just acquires the multiplier $a^{-\lambda}$. Indeed, $f(x/a)=a^{-\lambda}f(x)$. The general solution to this equation is,
\begin{eqnarray*} f(x)=Ax^{-\lambda} \end{eqnarray*}It is seen that this distribution cannot be normalized to 1 at $\lambda\ge1$, because the respective integral diverges. In order to avoid this difficulty a modified distributions is introduced,
\begin{equation} \tag*{(7)} f(x)=A x^{-\lambda}e^{-\gamma x^{-\sigma}} \end{equation}with $\sigma>0$ and
\begin{eqnarray*} A^{-1}=\gamma^{(\lambda+\sigma+1)/2}\sigma^{-1}\Gamma(\lambda+1/\sigma) \end{eqnarray*} |
| Figure 3 |
The exponential multiplier kills the singularity of $f(x)$ at small $x$. An example of such. distribution is shown in Figure 3 Of course, another suitable function can be used instead of the exponent.
The Student distribution is well known to all who deal with the statistical treatment of the result. This distribution looks as follows,
\begin{eqnarray*} f(x)=\frac2{\sqrt\pi B(1/2,n/2)}\left(1+\frac{x^2}n\right)^{-(n+1)/2} \end{eqnarray*}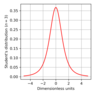 |
| Figure 4 |
It reveals the algebraic behavior at large $x$. Here $B(x,y)$ is the Euler beta function. Figure 4 displays the Student distribution for $n=3$.
Here we consider the simplest process that generates the Poisson distribution. The example given below is adopted from the demography but many similar processes are met in the geophysics.
The Malthus balance (the birth-death process $n-1\to n\to n_1$) is so primitive that nobody suspects that something unusual can stay behind. To our great surprise, it is not so, and an alternative consideration starting with the same idea that the change in population size comes from the difference between the birth and the death rates leads to rather unusual probability distribution of the sizes, although from the first sight, nothing except for the Poisson distribution is expected. The reality, however, occurs more complex.
First of all, let us formulate the balance equation for the probability $w(n,t)$ to find $n$ individuals in the population at time $t$ assuming the rates of the birth–death process to be linear in $n$. This equation claims,
\begin{equation} \tag*{(8)} \begin{array}{rcl} \frac{dw(n,t)}{dt}&=& \varkappa [(n-1)w(n-1,t)-nw(n,t)]- & &\lambda[ (n+1)w(n+1,t)-nw(n,t)]. \end{array} \end{equation}The right–hand side (RHS) of this equation describes the jumps $n-1\longrightarrow n$ (the birth process) and $n+1\longrightarrow n$ (the death process) that change the population size by $\pm1$ respectively.
In order to solve Eq. (8) we introduce the generating function for $w(n,t)$,
\begin{eqnarray*} F(z,t)=\sum\limits_{n=0}^\infty w(n,t)z^n. \end{eqnarray*}On multiplying both sides of Eq. (4) by $z^n$ and summing over all $n$ yield the first–order partial differential equation for $F(z,t)$,
\begin{equation} \tag*{(9)} \frac{\partial F}{\partial t}=(z-1)(\varkappa z-\lambda)\frac{\partial F}{\partial z}. \end{equation}It is easy to check that the general solution to Eq. (6) has the form:
\begin{equation} \tag*{(10)} F(z,t)=\psi\left(\frac{1-z}{\lambda-\varkappa z}e^{\mu t} \right). \end{equation}The function $\psi$ should be determined from the initial condition $F(z,0)=F_0(z)$ or
\begin{eqnarray*} F_0(z)=\psi\left(\frac{1-z}{\lambda-\varkappa z} \right). \end{eqnarray*}We introduce $z(\xi)$ as the solution to the equation $\xi=(1-z)/(\lambda-\varkappa z)$. Hence,
\begin{eqnarray*} z(\xi)=\frac{1-\lambda\xi}{1-\varkappa\xi} \end{eqnarray*}and
\begin{equation} \tag*{(11)} \psi(\xi)=F_0\left(\frac{1-\lambda\xi}{1-\varkappa\xi} \right). \end{equation}On substituting $\xi=[(1-z)/(\lambda-\varkappa z)]e^{\mu t}$ from Eq.(10) into Eq. (11) finally yields,
\begin{eqnarray*} F(z,t)=F_0\left(\frac{\lambda-\varkappa z-\lambda(1-z)e^{\mu t}}{\lambda-\varkappa z-\varkappa(1-z)e^{\mu t}} \right). \end{eqnarray*}For further analysis it is more convenient to have the generating function $F(z,t)$ in the form:
\begin{equation} \tag*{(12)} F(z,t)=F_0 \left(A+\frac {Qz}{1-\displaystyle\frac z{z_0}} \right). \end{equation}Here
\begin{eqnarray*} A=\frac{\lambda(e^{\mu t}-1)}{\varkappa e^{\mu t}-\lambda},\quad Q=\frac{\mu^2 e^{\mu t}}{(\varkappa e^{\mu t}-\lambda)^2}, \end{eqnarray*}and
\begin{eqnarray*} z_0=\frac{\varkappa e^{\mu t}-\lambda}{\varkappa(e^{\mu t}-1)} \end{eqnarray*}It is important to note that above three functions are always positive because $\text{sgn}(e^{\mu t}-1)=\text{sgn}(\varkappa e^{\mu t}-\lambda) =\text{sgn} (\varkappa-\lambda)$. Here $\text{sgn}(x)=1$ at positive $x$ and $\text{sgn}(x)=-1$ otherwise.
It is easy to find two first moments of $w(n,t)$. On differentiating Eq. (6) once over $z$ and putting $z=1$ reproduce Eq. (11) for $\bar n(t)=\sum_nnw(n,t)=\partial_zF(1,t)$. Repeating this operation gives the closed equation for $\partial_{zz}^2F|_{z=1}=\Phi_2(t)=\sum_n(n^2-n)w(n,t)$,
\begin{eqnarray*} \frac{d\Phi_2}{dt}=2\mu \Phi_2+2\varkappa\bar n. \end{eqnarray*}The solution to this equation is,
\begin{equation} \tag*{(13)} \Phi_2(t)=\left (\frac{\Phi_{2,0}}{\bar n_0^2}+\frac{2\varkappa}{\mu \bar n_0}\right)\bar n^2(t)-\frac{2\varkappa}\mu\bar n(t). \end{equation}Let us analyze the initial Poisson's distribution. In this case $\Phi_{2,0}=\bar n_0^2$. We calculate the difference $\Delta=\overline{n^2}(t)-\bar n^2(t)$. This difference is readily found from Eq. (13),
\begin{eqnarray*} \Delta(t)=\bar n(t)\left[1+\frac{2\varkappa}\mu(e^{\mu t}-1)\right]. \end{eqnarray*}It is interesting to note that $\Delta(t)$ grows linearly with time as $\mu\longrightarrow0$, $\Delta(t)=n_0(1+2\varkappa t$), whereas the total population size does not change.
Of great interest is thus to find the time dependence of the distribution explicitly. To this end we apply Eq. (12) to the function
\begin{equation} \tag*{(14)} F_0(z)=e^{\bar n_0(z-1)}. \end{equation}This initial generating function corresponds to the Poisson distribution Eq. (1)
The size distribution $w(n,t)$ is expressed through the contour integral of $F(z,t)$,
\begin{equation} \tag*{(15)} w(n,t)=\frac1{2\pi i}\oint\frac{F(z,t)}{z^{n+1}}dz. \end{equation}The integration goes counterclockwise along the contour surrounding the origin of coordinates in the complex plane $z$. On applying Eq. (4) to $F_0(z)$ given by Eq. (14) and substituting the result into Eq. (15) yield,
\begin{equation} \tag*{(16)} w(n,t)=\frac1{2\pi i}e^{-\bar n_0a(t)}\oint\exp\left(\frac{\bar n_0zQ(t)}{1-\displaystyle\frac z{z_0}} \right)\frac{dz}{z^{n+1}}, \end{equation}where
\begin{eqnarray*} a(t)=[A(t)-1]=\frac{\mu e^{\mu t}}{\varkappa e^{\mu t}-\lambda}. \end{eqnarray*}The function $a(t)\ge0$.
The integration in Eq. (16) is readily performed to give
\begin{equation} \tag*{(17)} \frac1{2\pi i}\oint\exp\left(\frac{\bar n_0zQ(t)}{1-\displaystyle\frac z{z_0}} \right)\frac{dz}{z^{n+1}}={\cal L}_n(\bar n_0Qz_0), \end{equation}where ${\cal L}_n(x)$ are the polynomials of the $n$–th order that can be expressed through Laguerre's polynomials $L_n(x)$ as follows:
\begin{eqnarray*} {\cal L}_n(x)=L_n(-z_0\bar n_0Q)-L_{n-1}(-z_0\bar n_0Q), \end{eqnarray*}where
\begin{eqnarray*} L_s(x)=\frac{e^{x}}{s!}\frac{d^s}{dx^s}x^s e^{-x}. \end{eqnarray*}In deriving Eq. (17) we used the fact that
\begin{eqnarray*} (1-z)^{-1}\exp(xz/(z-1))=\sum\limits_{n=1}^\infty L_n(x)z^n \end{eqnarray*}is the generating function for the Laguerre polynomials $L_s(x)$ [Lushnikov and Kagan, 2016].
From Eqs (16) and (17) we finally have,
\begin{eqnarray*} w(n,t)=e^{-\bar n_0a}z_0^{-n}{\cal L}_n(\bar n_0Qz_0). \end{eqnarray*}Let us consider a collection of sites occupied by $n_1,n_2\ldots n_G$ elements These occupation numbers are considered as random variables. Let the total number of the elements is fixed and equal to $K$. Let us try to find the probability to find $W(n)$ the probability to have exactly $n$ units in one of the site.
\begin{equation} \tag*{(18)} W(n)=\sum\Delta(n_1+n_2+\ldots n_g-K) \end{equation}where $\Delta(k)=1$ at $k=0$ and $\Delta(k)=0$ otherwise.
The summation on the right-hand side of Eq. (18) goes over all sites except the site with number $k$. Of course, the final result is independent of $k$. We apply the integral representation of $\Delta(k)$.
\begin{eqnarray*} \Delta(k)=\frac1{2\pi i}\oint\frac{dz}{z^{k+1}} \end{eqnarray*}where the integration contour surrounds the point $z=0$ and the integration goes in the counterclockwise direction. Then we have instead of Eq. (18),
\begin{equation} \tag*{(19)} W(n)=\frac1{2\pi i}\oint\prod\frac{dz}{z^{k+1}}=\frac1{2\pi i} \oint\frac{dz}{z^{K+1}}F^K(z) \end{equation}where
\begin{eqnarray*} F(z)=\frac1{2\pi i}\oint\frac{dz}{f(z)} \end{eqnarray*}At large $N$ the integral in Eq. (19) can be evaluated by the saddle point method. the result has the well familiar form:
\begin{eqnarray*} W(n)=\frac1{\sqrt{2\pi\sigma^2 }}\exp\left(-\frac{(x-x_0)^2}{2\sigma}\right) \end{eqnarray*}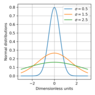 |
| Figure 5 |
Tht normal distribution is shown in Figure 5.
Let us consider the distributions evolving with time. A simplest example is the diffusion of aerosol particles in the atmosphere. This process is governed by the well–known diffusion equation,
\begin{equation} \tag*{(20)} \frac{\partial W}{\partial t}=D\frac{\partial^2W}{\partial x^2} \end{equation}Here $t$ is time, $x$ is the spatial coordinate of particle, $D$ is the diffusivity of the particle. The solution to this equation should depend a dimensionless group composed the values entering the diffusion equation. The only dimensionless combination composed of time, coordinate, and the diffusivity is $\zeta=x^2/Dt$. Therefore
\begin{equation} \tag*{(21)} W(x,t)=f(x^2/Dt) \end{equation}The function $f(\zeta)$ can be found by substituting Eq. (21) into Eq. (20). The final answer is,
\begin{equation} \tag*{(22)} f(\zeta)=\frac1{\sqrt{2\pi\zeta}}e^{\zeta^2/2}. \end{equation}A hundred years ago Smoluchowski (see [Friedlander, 2000]) formulated his salient equation that describes the coagulation process in aerosols. Since then the Smoluchowski approach found wide applications in numerous areas of physics, chemistry, economy, epidemiology, and many other branches of science [Adams and Seinfeld, 2002; Janson et al., 2001; Leyvraz, 2003; Pruppacher and Klett, 2006; Schmeltzer et al., 1999; Seinfeld and Pandis, 1998; Seinfeld, 2008].
From the first sight the coagulation process looks rather offenceless, a system of $M$ monomeric objects begins to evolve by pair coalescence of $g$– and $l$–mers according to the scheme,
\begin{eqnarray*} (g)+(l)\longrightarrow(g+l). \end{eqnarray*}And there is not a problem to write down the kinetic equation governing the process, everyone can do it, \begin{align}\label{23} \frac{dc_g}{dt}=I+\frac12\int\limits_0^gK(g-l,l)c_{g-l}c_ldl- \nonumber c_g\int\limits_{l=0}^\infty K(g,l)c_l dl. \end{align}
This is the famous Smoluchowski's equation. Here the coagulation kernel $K(g,l)$ is the transition rate for the process given by Eq. (22) which is assumed to br a homogeneous function of its arguments $K(ag,al)=a^\lambda K(g,l)$. The first term on the right–hand side (RHS) of Eq. (2) describes the gain in the $g$–mer concentration $c_g(t)$ due to coalescence of $(g-l)$– and $l$–mers, while the second one is responsible for the losses of $g$–mers due to their sticking to all other particles. In what follows we will use the dimensionless version of this equation, i.e., all concentrations are measured in units of the initial monomer concentration $c_0$ and the time in units of $1/c_0K(1,1)$. More details can be found in the review article [Leyvraz, 2003].
Here we consider a stationary version of this equation: we put $\partial_tc=0$ and, in addition, consider a simplified version of the kernel $K(g,l)=g^\alpha l^\alpha$. In this case Eq. (23) can be solved exactly. The result is,
\begin{eqnarray*} c_g=A g^{3/2+\alpha} \end{eqnarray*}where $A$ is a constant.
The random factors can affect the geophysical processes and change the shapes of the distribution. Here we consider two examples.
Let the population growth is governed by the Malthus equation .
\begin{eqnarray*} \frac{dn}{dt}=\kappa n-\lambda n=\mu n \end{eqnarray*}with $n(t)$ being the mean population size at time $t$, $\kappa$ and $\lambda$ are the birth and death rates respectively and $\mu=\kappa-\lambda$ being the growth rate coefficient. The population size grows at $\mu>0$ or falls at $\mu<0$)
\begin{eqnarray*} n=n_0e^{\mu t} \end{eqnarray*}Let us assume now that the rate coefficient is a random value distributed over the Gauss law
\begin{eqnarray*} W(\mu)=A\exp[-a(\mu-\mu_0)^2] \end{eqnarray*}where $A=\sqrt{\pi/a}$ is the normalization coefficient and $a$ is a dispersion parameter The distribution $W(\mu)$ is normalized to 1, i.e.,.
\begin{eqnarray*} \int_{-\infty}^\infty W(\mu)d\mu=1 \end{eqnarray*}We average $n(t)$ over the distribution $W$ and find,
\begin{eqnarray*} \bar n(t)=An_0\int_{-\infty}^\infty W(\mu) e^{\mu t}d\mu=n_0 e^{\mu_0 t}e^{t^2/4a} \end{eqnarray*}Hence, irrespective of the value of mean fertility the population swiftly grows The distribution function for $n$ can also be readily found. It is,
\begin{eqnarray*} w(n,t)= \sqrt{\frac\pi a}\int_{-\infty}^\infty W(\mu)\delta(n- n_0e^{\mu t})d\mu \end{eqnarray*}The integration gives the lognormal distribution
\begin{eqnarray*} w(n,t)= \sqrt{\frac\pi a}\frac1{tn}\exp\left[-\frac a{t^2}\ln^2(n/n_0)\right] \end{eqnarray*}Let us consider now the logistic growth
\begin{eqnarray*} \frac{dn}{dt}=\kappa n-\beta n^2-\lambda n=\mu n-\beta n^2 \end{eqnarray*}It is readily seen that the average population size
\begin{eqnarray*} \frac n{\mu-\beta n}=Ce^{\mu t} \end{eqnarray*}or
\begin{eqnarray*} n(t)=\frac{n_0e^x}{1+\beta n_0tF(x)} \end{eqnarray*}where
\begin{eqnarray*} F(x)=\frac{e^x-1}x\quad x=\mu t \end{eqnarray*}Now let us average this over the Gauss distribution centered at $\mu=\mu_0$.
\begin{eqnarray*} n(t)=\frac{n_0e^{\mu t}}{1+\beta n_0\frac{1-\exp(\mu t)}\mu}=\frac{n_0e^{\mu t}}{1+\beta n_0tF(\mu t)} \end{eqnarray*}where $F(x)=(1-e^x)/x$. On averaging this gives,
\begin{eqnarray*} \bar n(t)=n_0\int W(\mu)\frac{e^{\mu t}}{1+\beta n_0tF(\mu t)}dt \end{eqnarray*}For the logistic law the result is more complicated than in the case of the Malthus distribution
\begin{eqnarray*} w(n)=\int W(\mu)\delta\left[n-\frac{n_0e^{\mu t}}{1+\beta n_0tF(\mu t)}\right]d\mu \end{eqnarray*}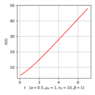 |
| Figure 6 |
Time dependence of the population size is shown in Figure 6.
We have presented several types of probability distributions widely used in geophysics (and not only) We have classified the geophysical random processes into two groups. The first group operates with random processes having a dominant structure i.e.,those including a deterministic process possessing all the feature of the whole process. In this case the task of the statistical study can be reduced to the search of this dominant process and the study the respective deterministic model underlying it. The randomness in this case reveals itself as corrections to the dominant process and plays the minor role. The example of such process is the waves on the oceanic surface or mountains on the Earth surface.
More sophisticated tasks appear in the cases where the dominant absents. The simplest example is the random walks of a billiard ball. Its coordinate of its stops cannot be predicted, neither its associated with some regular trajectories. It is clear that when such situations emerge we should attack it by using the probabilistic approaches
In both these cases the description goes in terms of the distributions. Sometimes these distribution can be found theoretically. If not, then we can chose a distribution from our collection and to try to match its parameters in such a way that the average characteristics would be reproduced.
Adams, P. J., J. H. Seinfeld (2002) , Predicting global aerosol size distribution in general circulation models, J. Geophys. Res., 107, no. D19, p. 4370, https://doi.org/10.1029/2001JD001010.
Bailey, N. T. J. (1964) , The Elements of Stochastic Processes, With Applications to Natural Sciences, 130 pp., John Wiley & Sons, Inc., New York–London–Sydney.
Barrett, J. C., C. F. Clement (1991) , Aerosol concentrations from a burst of nucleation, J. Aerosol Sci., 22, p. 327–335, https://doi.org/10.1016/S0021-8502(05)80010-2.
Ding, R., J. Li (2007) , Nonlinear finite-time Lyapunov exponent and predictability, Phys. Lett. A, 364, p. 396–400, https://doi.org/10.1016/j.physleta.2006.11.094.
Eckmann, J.-P., D. Ruelle (1985) , Ergodic theory of chaos and strange attractors, Rev. Modern Phys., 57, p. 617–656, https://doi.org/10.1103/RevModPhys.57.617.
Friedlander, S. K. (2000) , Smoke, Dust and Haze: Fundamentals of Aerosol Dynamics (2nd Edition), Oxford University Press, Oxford.
Golubkov, G. V., M. G. Golubkov, G. K. Ivanov (2010) , Rydberg states of atoms and molecules in a field of neutral particles, The Atmosphere and Ionosphere: Dynamics, Processes and Monitoring, Bychkov V. L., Golubkov G. V. and Nikitin A. I. (eds.), p. 1–67, Springer, New York, https://doi.org/10.1007/978-90-481-3212-6_1.
Golubkov, G. V., M. G. Golubkov, M. I. Manzhelii, et al. (2014) , Optical quantum properties of GPS signal propagation medium – $D$ layer, The Atmosphere and Ionosphere: Elementary Processes, Monitoring, and Ball Lightning, Bychkov V. L., Golubkov G. V. and Nikitin A. I. (eds.), p. 1–68, Springer, New York.
Janson, R., K. Rozman, A. Karlsson, H.-C. Hansson (2001) , Biogenic emission and gaseous precursor to forest aerosols, Tellus, 53B, p. 423–440, https://doi.org/10.3402/tellusb.v53i4.16615.
Julanov, Yu. V., A. A. Lushnikov, I. A. Nevskii (1983) , Statistics of particle counting in highly concentrated disperse systems, DAN SSSR, 270, p. 1140.
Julanov, Yu. V., A. A. Lushnikov, I. A. Nevskii (1984) , Statistics of Multiple Counting in Aerosol Counters, J. Aerosol Sci., 15, p. 69–79, https://doi.org/10.1016/0021-8502(84)90057-0.
Julanov, Yu. V., A. A. Lushnikov, I. A. Nevskii (1986) , Statistics of Multiple Counting II. Concentration Counters, J. Aerosol Sci., 17, p. 87–93, https://doi.org/10.1016/0021-8502(86)90010-8.
Klyatskin, V. I. (2005) , Stochastic Equations through the Eye of the Physicist: Basic Concepts, Exact Results and Asymptotic Approximations, 556 pp., Elsevier, Amsterdam, https://doi.org/10.1016/B978-0-444-51797-5.X5000-X.
Leyvraz, F. (2003) , Scaling theory and exactly solved models in the kinetics of irreversible aggregation, Phys. Rep., 383, p. 95–212, https://doi.org/10.1016/S0370-1573(03)00241-2.
Lushnikov, A. A., J. S. Bhatt, I. J. Ford (2003) , Stochastic approach to chemical kinetics in ultrafine aerosols, J. Aerosol Sci., 34, p. 1117–1133, https://doi.org/10.1016/S0021-8502(03)00082-X.
Lushnikov, A. A., A. S. Kagan (2016) , A linear model of population dynamics, Int. J. Mod. Phys. B, 30, no. 15, p. 1541008, https://doi.org/10.1142/S0217979215410088.
Mazo, R. M. (2002) , Brownian Motion: Fluctuations, Dynamics, and Applications, Oxford University Press, Oxford.
McKibben, M. A. (2011) , Discovering Evolution Equations with Applications: Volume 2. Stochastic Equations, 463 pp., Chapman & Hall/CRC, New York.
Michael, A. J. (2012) , Fundamental questions of earthquake statistics, source behavior, and the estimation of earthquake probabilities from possible foreshocks, Bulletin of the Seismological Society of America, 102, no. 6, p. 2547, https://doi.org/10.1785/0120090184.
Pruppacher, H. R., J. D. Klett (2006) , Microphysics of clouds and precipitation, Kluwer Academic, New York.
Schmeltzer, J., G. R'opke, R. Mahnke (1999) , Aggregation Phenomena in Complex Systems, Wiley–VCH, Weinbeim.
Seinfeld, J. H. (2008) , Climate Change, Review of Chemical Engineering, 24, no. 1, p. 1–65, https://doi.org/10.1515/REVCE.2008.24.1.1.
Seinfeld, J. H., S. N. Pandis (1998) , Atmospheric Chemistry and Physics, John Wiley & Sons, Inc., New York.
Van Kampen, N. G. (2007) , Stochastic Processes in Physics and Chemistry, 464 pp., Elsevier, Amsterdam.
Zagaynov, V. A., A. A. Lushnikov, O. N. Nikitin, et al. (1989) , Background aerosol over lake of Baikal, DAN SSSR, 308, p. 1087.
Received 12 November 2019; accepted 12 December 2019; published 17 December 2019.


Citation: Lushnikov A. A., Sh. R. Bogoutdinov (2019), An introduction to geophysical distributions, Russ. J. Earth Sci., 19, ES6010, doi:10.2205/2019ES000697.
Copyright 2019 by the Geophysical Center RAS.