RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 18, ES6007, doi:10.2205/2018ES000640, 2018
R. Yu. Lukianova1,2, Sh. R. Bogoutdinov1,3
1Geophysical Center of the Russian Academy of Sciences (GC RAS), Moscow, Russia
2St.Petersburg State University (SPbU), St.Petersburg, Russia
3Schmidt Institute of Physics of the Earth of the Russian Academy of Sciences (IPE RAS), Moscow, Russia
We report the initial results of the statistical analysis of field-aligned currents (FACs) observed above the ionosphere by the low-Earth polar-orbiting Swarm satellite. FACs are the main electrodynamic agent of the solar wind-magnetosphere-ionosphere coupling. FACs flow along the high-conducting geomagnetic field lines between the magnetospheric boundary layers and the auroral ionosphere. A series of the Swarm-based statistical maps of large-scale FACs are constructed, resolving the seasonal dependences of the FAC distribution under conditions of the northward and southward interplanetary magnetic field (IMF), low solar activity and the total IMF strength of 1-2 nT on average. The conventional R0/R1/R2 system is the dominant feature in the dark and sunlit polar ionosphere. The upward/downward current densities are well balanced within a given hemisphere, demonstrating a reasonable rate of elevation, going from winter to summer and from positive to negative IMF. The FAC intensities are larger by a factor of 1.6 in the summer hemisphere in comparison to the winter hemisphere.
Field-aligned currents (FACs) play an important role in coupling of the solar wind-magnetosphere-ionosphere system providing the channel for energy and momentum transfer between these domains. FACs flow along the high-conducting geomagnetic field lines between the magnetospheric boundary layers and the auroral ionosphere. In the conducting ionosphere, FACs induce the electric potential and horizontal currents, which are responsible for the motion of ionospheric plasma and for the geomagnetic variations measured on the ground.
Existence of FACs was theoretically predicted by Birkeland [1908]. However, until the satellite era there was no possibility to reveal these currents experimentally. According to the Fukushima theorem [Fukushima, 1976] FACs do not produce any magnetic effect on the ground (only together with the ionospheric Pedersen current), so that this effect can be measured only above the ionosphere. There, FACs can not be measured directly, and instead the magnetic variations in the orthogonal plane produced by FACs are measured, from which the current density is calculated.
 |
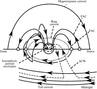
| Figure 1 |
A schematic distribution of large-scale FACs has been first established by Iijima and Potemra [1976] after the analyzing the magnetic variations measured by the Triad satellite. It was shown that the auroral FACs comprises a pair of sheets, namely, Region 1 (R1) and Region 2 (R2) with opposite current flow directions in the morning and evening sectors, and the polarity switch around noon and midnight [Iijima and Potemra, 1976]. The R1 and R2 FACs are part of the current loops connecting the magnetopause and inner magnetosphere and closing in the ionosphere primarily via Pedersen currents. Later additional FAC systems have been discovered: Region 0 (R0), which are observed on the day side poleward of the R1 sheets with polarity opposite to R1 in association with co-called `NBZ' current system during times of northward interplanetary magnetic field (IMF) [Bythrow, 1988; Zanetti et al., 1984]. If a substorm occurs, FACs form an additional current wedge in the magnetotail [Lui, 1996]. During the magnetic storm main phase FACs are partly connected to the ring current. Electric currents flowing in the magnetosphere-ionosphere system is schematically shown in Figure 1.
The large-scale morphology of R0/R1/R2 current systems, the factors influencing their strength and distribution as well as the evolution of the FACs in response to external condition changes are still under active investigation. It is now established that under stationary conditions the FAC systems are evolved in accordance with the dayside reconnection which is controlled by the interplanetary magnetic field (IMF). The FAC intensity also almost linearly depends on the ionospheric conductivity. Knowledge of these basics allows constructing the statistical empirical models of FACs.
The magnetic measurements on board of low Earth orbiting satellites crossing the polar regions provided an enormous database of the FAC-produced magnetic field variations above the high-latitude ionosphere. Studies focused on the empirical description of FACs, through preprocessing the space-born magnetic data, is based on binning them into discrete categories according to controlling factors such as IMF orientation and magnitude. Analysis of the magnetic data collected by the DE2 [Farthing et al., 1981], Magsat [Langel and Estes, 1985], {rsted [Neubert et al., 2001], Champ [Reigber et al., 2004], and Iridium/AMPERE [Anderson et al., 2000] satellites resulted in the appearance of several empirical models of FAC distribution parameterized by the IMF direction/strength, by season, and by hemisphere [Weimer, 2001; Papitashvili et al., 2002; Anderson et al., 2008; He et al., 2012]. Although the modeling results generally agree with each other, there are some differences between them, especially with respect of the near-pole FACs and the quantitative estimates of the response of FAC systems to changes in external conditions.
With the launch of the multi-satellite Swarm mission, equipped with the high precision vector magnetometers [Olsen et al., 2013], the technique of space measurements of FACs was considerably improved. Since the beginning of 2014 a great amount of new data has been collected, which were mostly used to study the internal part of the Earth magnetic field. The Swarm data also provide an opportunity for a better understanding of the external magnetic field and, in particular, the distribution of FACs. In the previous publications mostly the combined data set were analyzed. McGranaghan et al. [2017] examined the combined FAC data from the Swarm and the AMPERE (former Iridium) constellations and revealed features of the repeatable behavior of FACs across scales. Three satellite missions (Champ, {rsted, and Swarm) have been used to identify the effects of varying solar radiation on the magnitudes and locations of FACs [Edwards et al., 2017].
So far, no statistical distributions of FACs based solely on the Swarm observations have been presented. Because of this it is difficult to compare the results of the previous and current missions. In the present paper, as a step towards a construction of the FAC model based on Swarm-only measurements, we analyze the 2-year period of Swarm observations in order to reveal the seasonal and IMF $B_z$ dependences of FACs.
Swarm constellation consists of three closely spaced satellites, designated A, B, and C [Olsen et al., 2013]. At the initial phase of the mission Swarm A and C fly side by side at 460 km altitude, separated by 1.4${}^\circ$ in longitude. and Swarm B is at slightly higher orbits at 520 km. Swarm A and C are at an orbital inclination of 87.5${}^\circ$, and that of Swarm B is slightly higher, so that a 20${}^\circ$ increase occurs in the angle between the orbital planes per year. The satellites were launched in November 2013 and achieved final constellation configuration in April 2014. For the middle of 2018 the orbit altitude decreases down to $\sim$420 and 500 km, respectively. The satellites have 14–15 orbits per day. The time period, during which the satellite traverses the high-latitude region ($>$50${}^\circ$ magnetic latitude, MLat), is equal to $\sim$20 minutes. Slowly drifting in longitude, the orbits cover all the local time sectors over 7–10 months.
The main module of the Swarm payload is the high-sensitivity vector and scalar magnetometers. Using the vector fluxgate magnetometer measurements on board each spacecraft the Swarm science team routinely produce estimates of the FAC density. FAC estimates are based on Ampere's law and a model of the geomagnetic and magnetospheric magnetic fields. Single-satellite estimate is applied to all three satellites. Besides, the geometry of the Swarm constellation provides the opportunity to also estimate FACs with a dual-satellite approach. The dual-satellite estimate uses consecutive magnetometer measurements from Swarm A and C, located at a common altitude and separated by roughly 1.4${}^\circ$ in longitude, corresponding to $\sim$50 km at 70${}^\circ$ MLAT, to define a quad of four data points from which the integral form of Ampere's law can be evaluated [Ritter et al., 2013]. The 1-sec FAC values are available via the online Swarm data portal as Level 2 data products [Swarm Level 2 Processing System Consortium, 2012]. Level 2 FACs for Swarm A, B and C are routinely calculated using the single satellite approach. The data base also contains FACs calculated using the two-satellite approach from Swarm A and C. In the present study we utilize "the single satellite" FACs because their magnitude is larger than the "two-satellite" FACs.
We analyze Swarm data for the period spanning 2016–2017, and use single-satellite estimates from Swarm A, C and B. To bin the observations according to the external conditions we use 5-min resolution IMF data from NASA's Coordinated Data Analysis Web. These data contain measurements from multiple spacecrafts, accounting for estimated spacecraft-to-magnetopause propagation times. To adjust the IMF cadence to the duration of the satellite traversing of the high-latitude region the 5-min values were averaged to the 20-min values. An additional 15 min delay is applied to take into account the delayed response of FACs to the change in solar wind (SW), which includes the magnetosphere-ionosphere communication time and the FAC reconfiguration time itself. The IMF using the 5-min sliding window taken at the interval from 15 min before the satellite's magnetic field line footprint crosses $\pm$55${}^\circ$ MLat entering the polar cap and to the end of the polar pass. Note, that the 15-min delay is very approximate. Thus it may introduce an additional error to the statistical FAC distribution because the response of FACs (similar to the convection patterns) may be more or less delayed depending on the magnetic local time (MLT) sector [Lukianova and Kozlovsky, 2011].
There are two possible approaches to determine the FAC response to a change in the IMF. The first is to examine each individual event of the IMF change to perform a search of the associated details of the response. Such an analysis is more appropriate for the study of the response to a sudden change in the IMF orientation. The second approach is to average the data for revelation the most common features. Such approach is used for construction of the statistical models with binning of both IMF and FAC data [Papitashvili et al., 2002]. In the frame of this approach (which is used in the present study) the slow variations of the IMF may be accounted for.
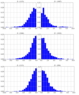 |
| Figure 2 |
Since we intend to bin the measured FACs into discrete categories according to the season and the IMF orientation, the first step is to select the time intervals during which the IMF is northward (IMF $B_z>0$) or southward (IMF $B_z<0$). Figure 2 shows the distribution of the magnitude northward (positive) and southward (negative) IMF $B_z$ for the 3-month seasonal intervals: equinox (September–November), summer (June–August) and winter (December–February) during the 2-yr period under consideration. From Figure 2 one can see that the intervals during which $|B_z|<2$ nT are the most common ($\sim$50%), while the occurrence of intervals of {\textbar}$B_z${\textbar}$\sim$5 nT is less than 5%. It is not surprising because of low solar activity during the period of Swarm operation. However, a sufficient statistics only exists for the quiet conditions. Thus from all polar passes during a certain season the data were selected satisfying the IMF conditions: $|B_z|<$2 nT (median $\sim$1 nT).
 |
| Figure 3 |
An example of the original 1-sec FAC density measured along the Swarm A pass over the northern polar ionosphere from dusk ($\sim$15 MLT) to dawn ($\sim$04 MLT) for a period of 23:50–00:13 UT on 8 Sept 2017 is shown in Figure 3. Superimposed to the 1-sec data the 21-point FFT smoothed curve is also shown. As seen, the FACs are located in the auroral zone, while the polar cap (MLat$>$75${}^\circ$MLat) is empty of currents. The original 1-Hz data contain a set of small-scale structures, while the smoothed curve reveals a multi-layer structure of the R1/R2 type. In the dusk side the large-scale downward (R2) and upward (R1) FAC sheets are detected. At 04–05 MLTs, several FAC downward/upward layers are observed. This multilayer structure is a signature of FACs, which are generated due to multiply reconnection processes occurred the in the magnetotail.
We used the Swarm observations in 2016–2017 to reveal the seasonal and IMF $B_z$ dependences of FACs. As shown by previous FAC observations and models, these parameters are the primarily factors influencing FACs. Solar illumination affects ionospheric conductivity and thus, in the frame of the "magnetosphere as a voltage generator" concept [Haraguchi at al., 2004], determines the intensity of FACs. The vertical ($B_z$) component of IMF is the most geoeffective one. The IMF $B_z$ primarily determines the rate of the dayside reconnection and thus the FAC configuration and intensity. If $B_z$ is southward ($B_z<0$), reconnection occurs on the day side, allowing a large amount of SW energy to enter the magnetosphere that results in the strengthening of FACs. If $B_z$ is northward ($B_z>0$), viscous-like SW-magnetospere interaction prevails. Viscous-like interaction occurs mostly in the magnetotail, that leads to reconfiguration and weakening of FAC system.
To obtain the statistical FAC distribution, first, the hemispheric high-latitude ($>50{}^\circ$ MLat) 1-Hz FAC data were binned into three seasonal categories. Then the FAC densities consecutively for all the orbits of the selected periods were binned according to the IMF $B_z$ magnitude and sign. For the MLT-MLat coordinate grid covering the high-latitude region poleward of MLat=50${}^\circ$ with the steps of 1${}^\circ$ in MLat and 15${}^\circ$ in MLong (1 hour in MLT) the FAC densities were collected within each grid cell. We can thereby obtain the spatial distribution of FACs in all MLT sectors.
 |
| Figure 4 |
Figure 4 shows the distributions of FACs (ionospheric footprints of FAC) inferred from the Swarm A and B data for northern winter (left), northern summer (middle), and fall equinox (right) polar caps; red regions are downward currents, and blue regions are upward currents, while white areas generally denote a lack of available data. The large-scale sheet-like structures are clearly seen in each plot. The area of lacking data near the pole is likely caused by the diurnal variation in the position of the magnetic pole (and thereby the entire magnetic coordinate system) with respect to the satellite orbit. As seen in Figure 4, the polarity of R1/R2 FACs corresponds to the classical picture by Iijima and Potemra. The R1/R2 system is the dominant feature even in the dark, winter hemisphere. The southern hemisphere, for the opposite seasons, shows a very similar FAC structures, although with larger blank area near-pole that is likely related to the larger offset of the geographic and geomagnetic poles (not shown).
A notable feature is a rotation of FAC system as a whole, which appears to be slightly different in summer, winter and equinox. As seen in the middle plots of Figure 4, clockwise rotation is a characteristic of the summer distribution. The FAC pattern is slightly (by $\sim$1 hr) skewed toward the dawn, so that the region of the focuses of current densities are located not at the dawn-dusk meridian but rather at the 02–14 MLT line. In the left plots (winter) the current sheets are more symmetric with respect to the noon-midnight meridian with a weak tendency to rotate slightly anticlockwise. The FAC patterns shown in the right plots (equinox) are well symmetric with respect to the noon-midnight meridian. The multilayer structures near noon are observed, mainly in summer and equinox.
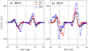 |
| Figure 5 |
To estimate the average location and strength of the upward/downward FACs, in Figure 5 we show the FAC densities versus MLat along the dusk-dawn meridian (18–06 MLT). It is seen that, irrespective of the season, the R1 FACs are located between approximately 70${}^\circ$ and 80${}^\circ$ MLat, while the R2 FACs occupy the latitudinal range of 60–70${}^\circ$ MLat. The nightside currents are slightly shifted to lower latitudes (by less than 5${}^\circ$ on average) compared to the dayside currents. The R1 currents are stronger than R2 by $\sim$40%. For a given IMF sign the current density increases going from summer to winter. For the peak values the inter-seasonal difference is about a factor of 1.5, if $B_z>0$, while it is reduced to a factor of 1.2, if $B_z<0$. If the IMF rotates from north to south, the FAC densities increase approximately by a factor of 2. Almost no asymmetry in the upward/downward current density is observed, if positive (downward) and negative (upward) currents are averaged separately.
Christiansen et al. [2002] defined the size of the polar cap (PC) by estimating the over-the pole distance between the average positions the ionospheric footprint of the dawn-dusk FACs in both the northern and southern hemispheres as $\sim$34${}^\circ$ independent of season. If the PC boundary is estimated as a maximum of R1 FAC, the Swarm observations provide approximately the same value ($\sim$32${}^\circ$). Under assumption that the FAC density is significantly enhanced within the auroral oval, our model may be used to estimate the auroral oval boundaries from FAC signatures. However, Xiong et al. [2014] have shown statistically that the approach for detecting the boundaries of enhanced FAC intensity works well under dark conditions but not in sunlit areas.
The original Swarm data, after a proper smoothing, reveal as the two-layer as the multi-layer large-scale structures. The two-layer system is mostly characteristic of the dawn and dusk, while the multi-layer FACs are observed near noon and midnight. Additional, NBZ-type FACs appear in the near-pole region above 80${}^\circ$ MLat, if $B_z$>0. In general, the R0/R1/R2 system is the dominant feature in the dark and sunlit polar ionosphere. The R1 currents are more intense compared to the current sheets adjusted to R1 from the pole and equator. If the IMF $B_z > 0$, the maximal current density of the upward/downward R1 FACs are -0.11/+0.12, -0.25/+0.22, -0.16/+0.18 $\mu$A/m${}^{2}$ in winter, summer and equinox, respectively. If the IMF is directed southward ($B_z<0$), the corresponding values are -0.24/+0.23, -0.42/+0.39, -0.30/+0.32 $\mu$A/m${}^{2}$.
The NBZ FAC sheets are developed as a reversed to R1 currents at the near-pole during the northward IMF, forming multi-sheet current systems. Relatively weak FACs are observed, mostly on the day side poleward of R1, even if $B_z<0$. Thus the basic R0/R1/R2 patterns are seen, but the maps show structures that are more complex and evolving as the IMF vector rotates. Interestingly, the statistical maps show features resembling the "current spiral" introduced theoretically by Siscoe and Maynard [1991] and also seen in the empirical model by Papitasvili et al. [2002]. In the maps obtained in the present study the spiral-like structure appears to be more pronounced in summer. The FAC pattern as a whole seems to rotate clockwise over the polar cap, showing R0/R1/R2 segments at the slightly later MLT hours.
Estimates of the average FACs over high-latitude regions under the IMF north- and southward condition the dawn and dusk MLT sectors. The ratio between the summer and winter R1/R2 summed densities is $\sim$1.6. Taking into account the similar difference ($\sim$1.8) in the ionospheric conductivity due to the solar illumination [Robinson and Vondrak, 1984], the large-scale FACs are associated with a voltage-like source in the magnetosphere. The ratio obtained is between the results by Fujii et al. [1981] (these authors found that the ratio is $\sim$2) and Christiansen et al. [2002] (the ratio is $\sim$1.5). Net current in a given hemisphere does not exceed 0.1 MA (i.e. less than 10% of the total FAC). This implies the marginal interhemispheric FACs, if the effect of the asymmetric reconnection in the magnetosphere associated with the azimuthal ($B_y$) IMF is not in action. However, in a given MLT sector the net current is often nonzero.
In the present study we do not touch the features of intra- and interhemispheric asymmetries in the FAC distribution. The asymmetric part of the FACs and electric field is controlled by the azimutal ($B_y$) component and manifests itself mainly at very high latitudes. As pointed out by Ruohoniemi et al. [2005] it is necessary to link the solar zenith angle with the IMF clock angle in order to fully characterize the high-latitude electrodynamics. Asymmetric FACs, which are controlled by the IMF $B_y$ and originate from the electric potential drop between the polar caps, can flow between the hemispheres [Lukianova et al., 2010]. A relatively intense convection vortex controlled by the IMF $B_y$ develops around the pole during summer and equinox that is confirmed by the radar observations [Lukianova et al., 2008]. In the FAC model by Papitashvili et al. [2002] rather intense FACs, the distribution of which depended mainly on the IMF $B_y$ sign, were obtained in the polar caps. The same features were shown by Korth et al. [2010]. On the other hand, the maps presented in [McGranaghan et al., 2017] do not contain the near-pole FACs. Further analysis of the Swarm FACs will be done in the future in order to resolve the interhemispheric asymmetry related to the IMF $B_y$ effect.
Another open question that will be addressed in a consequent study is the solar cycle dependences of FACs. Observations from the previous missions, Magsat and {rsted, whose data formed a basis for the previous, most comprehensive FAC model [Papitashvili et al., 2002; Christiansen et al., 2002] were carried out during solar maxima. The Swarm mission operates during the declining phase and minimum of the relatively low solar cycle 24. Thus a comparison of the FAC distributions inferred from the previous model and from the model based solely on the Swarm observations would make it possible to assess the solar cycle effect.
Statistical maps of large-scale FACs based on the high precision magnetic observations above the ionosphere, which were carried out by the low-Earth orbit Swarm satellite in 2016–2017, are constructed. A series of maps obtained in this study resolve seasonal dependences of the FAC distribution over the high-latitude ionosphere under conditions of the north- and southward IMF, low solar activity and the total IMF strength of 1–2 nT on average.
The FAC patterns obtained in this study confirm seasonal dependence in the global FAC system generated and maintained by the solar wind-magnetosphere interaction, in which the magnetosphere acts as the voltage generator. This generator produces FACs from the two main interaction processes: the viscous-like interaction of the solar wind plasma with the Earth's magnetosphere and reconnection of the IMF ($B_z$ component) with the geomagnetic field at the subsolar magnetopause.
The R0/R1/R2 system is the dominant feature in the dark and sunlit polar ionosphere. The FAC intensities are larger by a factor of 1.6 in the summer hemisphere in comparison to the winter hemisphere.
Anderson, B. J., K. Takahashi, B. A. Toth (2000), Sensing global Birkeland currents with Iridium engineering magnetometer data, Geophysical Research Letters, 27, no. 24, p. 4045–4048, https://doi.org/10.1029/2000GL000094.
Anderson, B. J., H. Korth, C. L. Waters, et al. (2008), Statistical Birkeland current distributions from magnetic field observations by the Iridium constellation, Annales Geophysique, no. 26, p. 671–687, https://doi.org/10.5194/angeo-26-671-2008.
Birkeland, K. (1908), The Norwegian Aurora Polaris Expedition 1902–1903, 994 pp., H. Aschelhoug & Co., Christiania, Norway.
Bythrow, P. F., T. A. Potemra, R. E. Erlandson, et al. (1988), Birkeland currents and charged particles in the high-latitude prenoon region: A new interpretation, Journal of Geophysical Research, 93, no. A9, p. 9791–9803, https://doi.org/10.1029/JA093iA09p09791.
Christiansen, F., V. O. Papitashvili, T. Neubert (2002), Seasonal variations of high-latitude field-aligned currents inferred from \Orsted and Magsat observations, Journal of Geophysical Research, 107, no. A2, p. SMP 5-1–SMP 5-13, https://doi.org/10.1029/2001JA900104.
Edwards, T. R., D. R. Weimer, W. K. Tobiska, et al. (2017), Field-aligned current response to solar indices, Journal of Geophysical Research: Space Physics, 122, no. 5, p. 5798–5815, https://doi.org/10.1002/2016JA023563.
Farthing, W. H., M. Sugiura, B. G. Ledley, et al. (1981), Magnetic field observations on DE-A and -B, Space Science Instrumentation, 5, p. 551–560.
Fujii, R., T. Iijima, T.A. Potemra, M. Sugiura (1981), Seasonal dependence of large-scale Birkeland currents, Geophysical Research Letters, 8, no. 10, p. 1103–1106, https://doi.org/10.1029/GL008i010p01103.
Fukushima, N. (1976), Generalized theorem for no ground magnetic effect of vertical currents connected with Pedersen currents in the uniform-conductivity ionosphere, Report of Ionosphere and Space Research in Japan, 30, no. 1–2, p. 35–40.
Gvishiani, A. D., R. Yu. Lukianova (2015), Geoinformatics and Observations of the Earth's Magnetic Field: The Russian Segment, Izvestiya: Physics of the Solid Earth, 51, no. 2, p. 157–175, https://doi.org/10.1134/S1069351315020044.
Haraguchi, K., H. Kawano, K. Yumoto, S. Ohtani, T. Higuchi, G. Ueno (2004), Ionospheric conductivity dependence of dayside region-0, 1, and 2 field-aligned current systems: statistical study with DMSP-F7, Annales Geophysicae, no. 22, p. 2775–2783, https://doi.org/10.5194/angeo-22-2775-2004.
He, M., J. Vogt, H. Lühr, E. Sorbalo, A. Blagau, G. Le, G. Lu (2012), A high-resolution model of field-aligned currents through empirical orthogonal functions analysis (MFACE), Geophysical Research Letters, 39, no. 18, p. L18105 1–6, https://doi.org/10.1029/2012GL053168.
Iijima, T., T. A. Potemra (1976), The amplitude distribution of field-aligned currents of northern high latitudes observed by Triad, Journal of Geophysical Research, 81, no. 13, p. 2165–2174, https://doi.org/10.1029/JA081i013p02165.
Korth, H., B. J. Anderson, C. L. Waters (2010), Statistical analysis of the dependence of large-scale Birkeland currents on solar wind parameters, Annales Geophysicae, 28, no. 2, p. 515–530, https://doi.org/10.5194/angeo-28-515-2010.
Langel, R. A., R. H. Estes (1985), The near-earth magnetic field at 1980 determined from Magsat data, Journal of Geophysical Research: Solid Earth, 90, no. B3, p. 2495–2509, https://doi.org/10.1029/JB090iB03p02495.
Lui, A. T. Y. (1996), Current disruption in the Earth's magnetosphere: Observations and models, Journal of Geophysical Research: Space Physics, 101, no. A6, p. 13067–13088, https://doi.org/10.1029/96JA00079.
Lukianova, R., C. Hanuise, F. Christiansen (2008), Asymmetric distribution of the ionospheric electric potential in the opposite hemispheres as inferred from the SuperDARN observations and FAC-based convection model, Journal Atmospheric and Solar-Terrestrial Physics, no. 70, p. 2324–2335, https://doi.org/10.1016/j.jastp.2008.05.015.
Lukianova, R. Yu., A. Kozlovsky, F. Christiansen (2010), Asymmetric structures of field-aligned currents and convection of ionospheric plasma controlled by the IMF azimuthal component and season of year, Geomagnetism and Aeronomy, 50, no. 5, p. 667–678, https://doi.org/10.1134/S0016793210050142.
Lukianova, R., A. Kozlovsky (2011), IMF $B_y$ effects in the plasma flow at the polar cap boundary, Annales Geophysicae, 29, no. 7, p. 1305–1315, https://doi.org/10.5194/angeo-29-1305-2011.
McGranaghan, R. M., A. J. Mannucci, C. Forsyth (2017), A comprehensive analysis of multiscale field-aligned currents: Characteristics, controlling parameters, and relationships, Journal of Geophysical Research: Space Physics, 122, no. 12, p. 11,931–11,960, https://doi.org/10.1002/2017JA024742.
Neubert, T., M. Mandea, G. Hulot, R. von Frese, F. Primdahl, et al. (2001), \Orsted satellite captures high-precision geomagnetic field data, Eos Trans. AGU, 82, no. 7, p. 81–88, https://doi.org/10.1029/01EO00043.
Olsen, N., E. Friis-Christensen, R. Floberghagen, et al. (2013), The SWARM satellite constellation application and research facility (SCARF) and SWARM data products, Earth, Planets and Space, no. 65, p. 1189–1200, https://doi.org/10.5047/eps.2013.07.001.
Papitashvili, V. O., F. Christiansen, T. Neubert (2002), A new model of field-aligned currents derived from high-precision satellite magnetic field data, Geophysical Research Letters, 29, no. 12, p. 28-1–28-4, https://doi.org/10.1029/2001GL014207.
Reigber, C., H. Lühr, P. Schwintzer, J. Wickert (2004), Earth Observation with CHAMP. Results from Three Years in Orbit, 629 pp., Springer-Verlag, Berlin, Germany.
Ritter, P., H. Lühr, J. Rauberg (2013), Determining field-aligned currents with the Swarm constellation mission, Earth, Planets and Space, no. 65, p. 1285–1294, https://doi.org/10.5047/eps.2013.09.006.
Robinson, R. M., R. R. Vondrak (1984), Measurements of $E$ region ionization and conductivity produced by solar illumination at high latitudes, Journal of Geophysical Research: Space Physics, 89, no. A6, p. 3951–3956, https://doi.org/10.1029/JA089iA06p03951.
Ruohoniemi, J. M., R. A. Greenwald (2005), Dependencies of high-latitude plasma convection: Consideration of IMF, seasonal, and UT factors in statistical patterns, Journal of Geophysical Research, 110, no. A9, p. A09204 1–24, https://doi.org/10.1029/2004JA010815.
Siscoe, G., N. Maynard (1991), Distributed two-dimensional region 1 and Region 2 currents: Model results and data comparisons, Journal of Geophysical Research: Space Physics, 96, no. A12, p. 21071–21085, https://doi.org/10.1029/91JA02369.
Swarm Level 2 Processing System Consortium., (2012), Detailed Processing Model (DPM) FAC, Tech. Rep. SW-DS-GFZ-GS-0002: Swarm Level 2 Processing System, GFZ, Potsdam, Germany.
Weimer, D. R. (2001), Maps of ionospheric field-aligned currents as a function of the interplanetary magnetic field derived from Dynamics Explorer 2 data, Journal of Geophysical Research: Space Physics, 106, no. A7, p. 12889–12902, https://doi.org/10.1029/2000JA000295.
Xiong, C., H. Lühr, H. Wang, M. G. Johnsen (2014), Determining the boundaries of the auroral oval from CHAMP field-aligned current signatures – Part 1, Annales Geophysicae, 32, no. 6, p. 609–622, https://doi.org/10.5194/angeo-32-609-2014.
Zanetti, L.J., T.A. Potemra, T. Iijima, et al. (1984), Ionospheric and Birkeland current distributions for northward interplanetary magnetic field - inferred polar convection, Journal of Geophysical Research: Space Physics, 89, no. A9, p. 7453–7458, https://doi.org/10.1029/JA089iA09p07453.
Received 20 October 2018; accepted 11 November 2018; published 27 December 2018.


Citation: Lukianova R. Yu., Sh. R. Bogoutdinov (2018), Statistical maps of field-aligned currents inferred from Swarm: dependence on season and interplanetary magnetic field, Russ. J. Earth Sci., 18, ES6007, doi:10.2205/2018ES000640.
Copyright 2018 by the Geophysical Center RAS.