RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 18, ES4004, doi:10.2205/2018ES000627, 2018
A. D. Gvishiani1,2, F. S. Roberts3, I. A. Sheremet4
1Schmidt Institute of Physics of the Earth of Russian Academy of Sciences, Moscow, Russia
2Geophysical Center of the Russian Academy of Sciences, Moscow, Russia
3Rutgers University, New Brunswick, New Jersey, USA
4Financial University under the Government of Russian Federation, Moscow, Russia
This paper is dedicated to the analysis and comparison of various mathematical toolkits, applicable to the assessment of sustainability/vulnerability of distributed sociotechnical systems (DSTS) to natural disasters. A "black box"-based general description of the DSTS operation is given. This description is used for consideration of capabilities and limitations of mathematical models of DSTS, known from the operations research and knowledge engineering areas. All tools mentioned are compared by representation of DSTS operational logic, impacts on DSTS, and criteria for recognition of a system's sustainability. Algorithmic and implementation issues are discussed. Conclusions about applicability of the tools to the problem of sustainability/vulnerability of DSTS and possible future developments are presented.
One of the most pressing and at the same time complicated problems of applied system analysis today is assessment of sustainability of modern distributed sociotechnical systems (DSTS) to various destructive impacts – first of all, natural disasters (ND) [Dubois and Gvishiani, 1998; Gvishiani and Dubois, 2002; Gvishiani et al., 2008, 2014, 2016].
By digitization, robotization and networking, DSTS become more and more "technical", interconnected, and, thus, vulnerable to even local malfunctions of devices entering these systems, as well as to loss of some relatively small parts (bulks) of resources necessary for their operation. Every such malfunction or loss, by multiple chain, or cascading, effects, may lead to serious negative consequences, which may occur far beyond the place (area) of initial technical accident launched by ND [Roberts, 1982].
So it is extremely important to assess and, even more useful, to predict the afore-mentioned consequences by application of models of DSTS along with data describing their current state.
In this context, a choice of basic mathematical toolkit for the assessment of DSTS sustainability/vulnerability to real or possible destructive impacts is a key factor defining future success or failure of the developed model's application to the existing or designed systems.
The problem described above is not absolutely new, and, in different variations, it was studied in many known works [Adams and Jeanrenard, 2013; Bakari, 2017; Black and Cherrier, 2010; Geissdoerfer, 2017;
Le Billon, 2005; Pearce, 2012; Roberts, 2011; Sheker, 2015; Waite, 2013; Wright, 2004]. This paper is dedicated to the analysis and comparison of mathematical toolkits used in previous publications concerning the problem of interest.
To compare capabilities and limitations of various toolkits we shall begin with introducing in Section 2 some generalized intermediate description of DSTS, based on a "black box" representation of their elementary operational units (devices, robots, human-controlled manufacturing or transporting subsystems, etc.). This representation will be used for consideration of different approaches to DSTS modeling, based on scheduling theory (Section 3), Petri nets (PN, Section 4), network models and mathematical programming (Section 5), logic programming (LoP), deductive data bases (DDB), constraint programming (CP), and multiagent systems (MAS, Section 6), as well as on multiset grammars (MG, Section 7). Final comparison will be made in Section 8, where also some conclusions about further development will be presented.
 |
| Figure 1 |
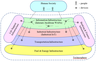
A digital economy (DE) paradigm [Huws, 2015; The New Digital Economy, 2011; Tapscoft, 1997] simplifies and unifies representation of all possible sociotechnical systems, which, independently of their functions, may be naturally described in the network-centric framework. According to modern views, accumulated, for example, in the Industry 4.0 concept [Herman et al., 2016; Ustundag and Cevicsan, 2017], any human society operates as a set of customers (human beings) connected by common Internet-based information infrastructure with a set of various devices, forming together industrial, transportation, energy, life support, and banking and finance infrastructures (Figure 1). This set of devices, usually called Internet of Things (or if it is considered mainly a manufacturing process, Industrial Internet of Things), provides for the creation of the items (products and resources) ordered by customers, and their relocation to the places of their usage. The process of item creation in the general case includes multiple operations, executed by various manufacturing devices, located more or less far from one another, and also transportation of the items and their elements (spare parts) from places where they are produced to places where they are used. In the most advanced cases, where industrial infrastructure implements additive technologies of manufacturing, e.g., 3D-printing, the afore-mentioned logistics is the simplest and includes transportation of necessary amounts of powders from their storage to 3D-printers, and, after the manufacturing cycle is finished, transportation of the printed items to the customers. In parallel with relocation of material objects, payments for the works done are performed in electronic form by application of banking and finance infrastructure capabilities.
Operation of all devices, including networking hardware, as well as of acting personnel, is based on the consumption of electrical energy produced by power plants and transferred by electrical grids, forming an energy infrastructure that is often considered as a whole with fuel storages, pipelines, as well as with fuel stations. Relocation of products and persons is performed by various vehicles upon rail-roads, highways, water and air routes, and all these vehicles utilize fuels and/or electrical energy (the last in the case of electric vehicle transport).
Life support infrastructure includes technical objects, providing people residence, food, water supply and other services (including emergency, healthcare, etc.) necessary for their existence and functionality.
The described process of the DSTS operation is highly decentralized, and the interaction between devices is organized in a peer-to-peer mode via information infrastructure. Formal description of such complicated systems is possible if there is some unified representation of the main elements and their functional interconnections and interdependencies.
Let us begin with the simplest case, when the sociotechnical system (STS) is local. Such system may be explicated as a set of devices (also called lower technological base, TB).
 |
| Figure 2 |
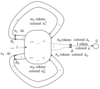
Each such device may be represented as a "black box" $B$ with $k$ inputs and $l$ outputs (Figure 2a). We shall mark the $i$-th input by $a_i$, which $a_i$ is the name of the resource type, and mark by $n_i$ the amount (volume, quantity) of such resource elementary units (or units of measurement).
This means $n_i$ units of resource $a_1, \ldots, n_k$ units of resource $a_k$ are required to device $B$ for creation (producing, manufacturing) of $n_1'$ units of resource $a_1', \ldots, n_l'$ units or resource $a_l'$. Also there exists some initial collection of resources $I$, called the resource base (RB) of STS, containing $m_1$ units of resource $a_1^{"}, \ldots, m_N$ units of resource $a_n^{"}$. The created resources enter the resource base and may be extracted from RB by any device, that may start an operation cycle at any moment, when RB contains all resources, defined by its inputs. Let us underline, that STS operates in the presumption, that there are no pauses in every device operation: as soon as all necessary resources are available, the next operation cycle of device begins (of course, if two or more devices need the some resources, there are may be various ways of STS operation, differing by sequence of competing devices activation).
By locality of STS, resource exchanges between RB and devices are presumed immediate. Process of STS operation is driven by the flow of input orders (Figure 2b). Each such order defines a collection of resources, i.e., $\bar{n}_1$ units of resource $\bar{a}_1, \ldots, \bar{n}_p$ units of resource $\bar{a}_p$, which must be created by the system.
As may be seen from Figure 2b, an input order may be also represented as the same "black box" with inputs, corresponding to an order-defined resource collection, and an output, being order identifier.
It is essential, that there are no firm (rigid) links between devices for resource exchange; instead of such links a more general and flexible scheme can be implemented, providing the afore-mentioned exchange via the resource base.
Clearly, every operation cycle of any device $B$ is executed during some time interval. Due to the unified representation this information is simply implanted to every "black box" as specific resource $\Delta t$, which amount $n$ is duration of the mentioned interval, measured in the fixed unit $\Delta t$ (second, minute etc.).
The only substantial difference between resource $\Delta t$ and other resources is that $\Delta t$ is not fully additive, because all devices, entering STS, may operate in parallel; time is additive only in relation to one device, i.e., to produce $n$ items, each created during $m$ time units $\Delta t$, the device would operate for $n \cdot m$ time units $\Delta t$. But if there are two or more such devices they would produce the afore-mentioned $n$ items during time $l \cdot \Delta t < n \cdot m \cdot \Delta t$ due to parallel operation of the devices and rational distribution of jobs among them.
Time may also enter an order in such a way that along with resource amounts required for the customer, it may contain time interval $n \cdot \Delta t$ as the precise duration of order completion or upper bound ("no more than $n \cdot \Delta t$") of this duration. Along with these two cases there may be a third one, where $n \cdot \Delta t$ is declared by the customer as the minimum of all possible values corresponding to various possible ways of completing an order. Also, a customer may include into the order amounts of some resources available while the order is completed, so there may be spent no more than the declared amount of every listed resource, or even the minimum of all possible values. These restrictions may be established by the customer as well as by producing STS, or as a result of their mutual agreement.
As may be seen from this short description, an order declared by the customer may be represented as a couple $ < G, R > $, where $G$ is list of resources being the goal of the request, while $R$ is a list of restrictions on amounts of resources and time available for the achievement of the goal. One of the most common resources (spent and restricted) is money.
Let us emphasize once more that time restrictions may be various; they may define that order may be completed:
To achieve the goal represented by couple $< G,R >$, there must be created a plan, or schedule, including operations synchronized by time and resources, executed by devices ("black boxes") entering the STS. Every such operation begins from extraction from the resource base the necessary amounts of resources, and finishes by the addition of a created object to the RB.
It is quite evident that creation of such a schedule is a sophisticated combinatorial problem, and development of algorithms providing efficient search of solutions of this problem is one of the most important tasks that must be carried out to create a rational digital economy.
For the above purpose there would be a special device – an intelligent component of STS, – creating schedules of order completion. This component will be called an STS scheduler (STS-S), and a similar abbreviation will be used for distributed STS schedulers (DSTS-S).
 |
| Figure 3 |
Production of an STS-S, i.e., a schedule, may be represented in a form similar to a Gantt chart (Figure 3), which contains $K$ parallel axes, each corresponding to its own device ("black box") $B_i$. The time interval $[t_j^i, t_j^i + \Delta_i]$, marked by start and finish points on the $i$-th axis, represents one operation cycle of $B_i$, which, let us recall, begins from the extraction of necessary amounts of resources from the resource base at moment $t_j^i$, their processing, creation of output object, and its transfer to the RB at moment $t_j^i + \Delta_i$. All such operations are synchronized by a unitary time scale for all $K$ times axes, and an operation cycle of $B_i$ may start only in that time interval when the resource base contains all amounts of resources defined by $B_i$ inputs, i.e., as soon as RB contains such amounts. In the general case various devices may compete for resources; and the start of one of them initiates delay of the others. Construction of a schedule providing order completion requires massive search in the solutions space, and various algorithms, implemented by corresponding STS-S, may differ by computational complexity of such search.
Let us consider more general cases concerning local STS application and operation.
"The closest" generalization of the described area is the same STS, which provides completion of the flow of orders in such a way that each next order may enter STS during processing of previous orders. The simplest but worst discipline of such flow handling is sequential, i.e., when STS begins to execute operations providing the next order completion after the previous order is already completed. However, to achieve maximal productivity, STS-S would provide maximal parallelization of sequentially incoming orders: operations providing completion of every incoming order would begin as soon as possible, in parallel with operations already executed to complete earlier orders. Thus STS-S operates upon flow of orders processed in the parallel mode.
There may be two approaches to such an STS schedule. The first is based on the presumption that schedules providing completion of previous orders are not corrected during creation of a schedule providing completion of the next entering order. The second approach is based on the possibility of correction of the already executed schedules while creation of the next one takes place. Of course, possible correction would not cause any previous order failure, which would shift this order terms out of its deadline.
Further generalization concerns the set of cases where STS during their operation may become the object of a natural hazard that destroys some resources and devices of the system. In such situations the task of STS-S is to reschedule system operation according to the new state of the system, i.e., its reduced resource base and technological capabilities. Rescheduling must be performed in such a way that all orders would be completed with minimal shift of terms and minimal amounts of spent resources or, if possible, without shift or spent resources.
A more complicated case, associated with the destructive impacts, addresses chain (or cascading) effects. Such effects emerge in propagation and multiplication of failures (damage) without additional impacts from the external sources, but only by reason of the existing internal interconnections between the affected STS subsystems (elements); the destruction (malfunction) of such an interconnection causes immediate or delayed destruction (malfunction) of its neighboring (in space and/or functional sense) elements. For example, failure of an electrical power plant causes failure of electricity-driven railway transport as well as of fuel stations that provide refueling of automotive transport, even if there is no direct impact on the transportation vehicles; as a consequence, all ground transport loses an ability to relocate resources and products necessary for industrial facilities that produce goods and food for human beings. These industrial facilities also fail, and so on.
The objective of all considered STS-S applications is the creation of schedules providing completion of all orders entering STS. However, in some circumstances (for example, after the afore-mentioned ND destructive impacts), there may also be a negative result when some of the orders can not be completed under the current resource and time restrictions.
So one more regime of an STS-S application would provide assessment as to what amounts of resources and devices would be produced (acquired) and added (included) to STS to complete the already processed orders. Furthermore, it is extremely important to know what time and resources are necessary to restore STS technological capabilities and resource base, because resources, which must be added after the destructive impact, must be, in turn, produced (manufactured). Thus, impacts generate an additional flow of orders, providing restoration of the affected STS through its part that had remained in the normal state, or/and by some external sociotechnical systems.
Let us also note that, as everywhere in system analysis, there may be two variants of STS – closed and open. Closed STS operate upon a resource base that is not restored from the outside environment (or metasystem); the last generates only "destructive" impacts. Open STS, by contrast, also provides RB restoration. However, this case may be reduced to the previous one by considering restoration as a "constructive" impact, which "affects" STS by adding some resources to RB instead of eliminating them. Thus, we unify rescheduling initiated by RB restoration through the already considered case of the "destructive" impact.
However, in the general case there may be situations, where neither the STS' own capabilities nor the metasystem's possible help can provide for order completion. That is why another necessary regime of an STS-S application, concerning STS in an affected state, as well as in its normal state, is the assessment of what part of the order may be completed given available resources. This function is extremely useful if there is no opportunity for the restoration of RB and the destroyed part of the technological capabilities of STS.
All that we have said above concerns local STS.
Let us consider now the general case – a distributed sociotechnical system. Formalizing this case, we shall follow the "Occam's razor" ideology and use previous constructions and entities, extending them by a minimal number of additional items.
Namely, we shall represent DSTS in the same way as local STS, adding to every resource collection containing units of some resource its location. We shall do the same with inputs and outputs of "black boxes", adding locations to the names of resources. By this we implant all necessary geospatial information into the representation of technological and resource bases of local sociotechnical systems, thus providing a unified form of the representation of technological and resource bases of the distributed STS. Similarly, geospatial information may be added to orders, which also consist of the afore-mentioned resource collections.
There will be the only syntactic extension for a located resource representation – instead of $a$ as names of resources we shall use constructions $a/p$ where "/" is a divider, and $p$ is the name of the point (place, area) where $a$ is located. By this minor change we expand representation of a local sociotechnical system, its resource base and order on the distributed STS. From this moment RB $I$ contains $n_1'$ units of resource $a_1'$ located at point $p_1', \ldots, n_k' $ units of resource $a_k'$ located at point $p_k'$. Similarly, a "black box" provides creation of one unit of resource $a$, located at point $p$, if there are $n_1$ units of resource $a_1$ located at point $p_1, \ldots, n_m $ units of resource $a_m$ located at point $p_m$, during a time interval of $n_0$ time units $t$. And, at last, the order defines $\bar{n}_1$ units of resource $\bar{a}_1$ located at point $\bar{p}_1, \ldots, \bar{n}_l $ units of resource $\bar{a}_l $ located at point $\bar{p}_l $.
The presence of locations in all of the components of the described intermediate formalization of DSTS provides a natural, flexible and simple representation of logistical capabilities of such systems, including both transportation and storage logistics. Storage located at point $p$ may be modeled by presence in the resource base $I$ of collections, containing $n_I'$ units of resource $a_I'$ located at $p, \ldots, n_I'$ units of resource $a_I'$ located also at $p$. Transportation capabilities, providing relocation of one unit of resource $a$ from point $p$ to point $p'$ may be simply modeled by the "black box" with input $a/p$ with number 1, output $a/p'$, and inputs representing amounts of resources necessary for this operation (among these resources may be an engaged transportation tool, i.e. cargo, ship etc., amounts of fuel necessary for this tool and transported resource relocation from $p$ to $p'$, and some others). As may be seen, any such approach to transportation operations modeling unifies all objects participating in relocation – active (transporting) as well as passive (transported).
The impact of a natural hazard may be represented in the described framework as a set of locations affected by the ND, so the result of the impact may be modeled simply by eliminating of all resource collections whose locations enter the given set. If destruction is partial, the impact may be represented as in the local STS case, i.e., in a form of a list of eliminated collections.
As may be seen from the description presented, a unified representation of distributed and local sociotechnical systems makes redundant the development of a special scheduler for DSTS. Thus, there is one general problem for solution, i.e., development of unitary algorithms for various types of orders, flows of orders and flows of impacts on DSTS resources.
From the infological point of view, every DSTS is a network-centered system based on Internet of Things protocols, providing devices ("black boxes") connection to the system integrating network and their mutual data exchange. We presume that the afore-mentioned protocols provide for informing of DSTS-S in the "business-as-usual" mode, but also in various abnormal situations caused by natural hazards leading to destruction and malfunction of devices. This may serve as a background for further consideration of one of the key problems of creation of a digital economy – DE optimal (or, at least, rational) scheduling on the whole life cycle and in the full spectrum of situations. We shall use this background for consideration of capabilities and limitations of the known mathematical toolkits that may be used for DSTS representation and DSTS-S algorithm development.
 |
| Figure 4 |
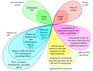
The total set of DSTS-S tasks and their mutual interconnections is presented in Figure 4 in a form of the "flower" whose "petals" correspond to the described directions of the considered sociotechnical systems classification. Each "petal" extends from the simple to the more complicated case, thus every tuple of five different values (more or less bulky) defines a specific subclass of DSTS and, thus, a complex of problems that must be solved while development of algorithms of schedulers for this subclass. This development may now be organized in the most rational direction – from simple to complex. As may be seen there are $ 2 \cdot 2 \cdot 4 \cdot 2 \cdot 2 = 64$ classes of problems to be solved.
The problems described in the previous sections, in some more or less general formulation, were considered in many earlier works from the operations research area and various segments of theoretical computer science.
Perhaps the closest to the set of tasks presented in Figure 4 are models and algorithms developed in scheduling theory. Various asynchronous systems, operating upon limited resources, are modeled by different classes of Petri nets. Models of optimal resource distribution and transportation are thoroughly considered in the operations research area by means of various matrix and network optimization models.
Along with classical approaches to formulation and solution of tasks, described earlier, some innovation models are used that also have potential for efficient application to these tasks: logic programming, constraint programming, deductive data bases, multiagent systems, and multiset grammars.
Let us consider the listed approaches in more detail.
Among many problems in the area referred to as scheduling theory [Brucker, 2001; Chatfield and Johnson, 2013; Pegden, 2009; Pinedo, 2008; the Resource Constrained Project Scheduling Problem (RCPSP) is, from a substantive point of view, the most general and useful in the application to the assessment of DSTS sustainability. RCPSP algorithms are used in the mostly well-known and widely applied production scheduling software, implementing a wide spectrum of useful features: material planning, job scheduling, capacity planning, bottleneck optimization, automated rescheduling, "what if" scenarios, priority-based scheduling, etc. (https://www.jobpack.com; https://www.clarity-software.com/wp-content/themes/melt_default/brochure/claritydigitalbrochure.pdf). RCPSP operates so called reusable (active) resources (RR), which are similar to the devices ("black boxes") in the above intermediate formalization.
A reusable resource becomes available (may be activated) immediately after finishing its previous operation cycle, which may begin when all un-reusable (passive) resources necessary for this operation are also available. Also there is a precedence relation upon the set of RR, which defines that RR $i$ must be completed before RR $j$ would be activated (or RR $j$ may be activated only after RR $i$ completion). Every RR has its own duration of operation cycle.
The problem is to create such a schedule, i.e., Gantt chart, which provides minimum time of completion of all projects, or, what is the same, the maximum of all finish times of RR involved in project completion. This value is called makespan.
RCPSP is one of the large number of problems considered in the scheduling theory segment called constraint-based scheduling (CBS) [Baker and Trietsch, 2009; Baptiste et al., 2001], the background for which is constraint programming, already mentioned above.
Also there is the so called "energetic reasoning", usually associated with CBS. This feature provides representation of non-reusable resources necessary for RR operation; however, all possible varieties of such resources are reduced to only one – energy.
Along with RCPSP, the most common implementation by software involves algorithms for the so called Preemptive Job-Shop Scheduling Problem (PJSSP), which is formulated as follows. There is set of jobs and set of machines. Each job consists of a set of activities to be processed in a given order. Each activity is associated with a processing time and a machine on which it has to be processed. Activities may be interrupted an unlimited number of times. Each machine can process no more than one activity at a time. The schedule to be created must minimize the makespan, which in this case is time, when all activities are finished. PJSSP is solved by application of constraints, worked out for this problem through a solutions search; such an application is called "constraint propagation".
There are RCPSP and PJSSP variations, very close to the spectrum of problems described in the previous section. These variations are usually considered inside a special segment of scheduling theory called "robustness and decision making" [Baker and Trietsch, 2009]. As it is said in [Baker and Trietsch, 2009], "in practice, it often happens that soon after a schedule has been generated, an unexpected event happens that forces the decision-maker to make changes".
However, modern scheduling theory as a whole is based on the primary consideration of reusable (active) resources. Mutual interconnections and interdependencies of the considered works (activities) must be apriori known and defined by input data. The fact that these interdependencies are a consequence of RR mutual exchange by unreusable (passive) resources, and project scheduling is, in fact, "passive resources-driven", comes out of the modern scheduling theory mainstream.
Petri nets are a flexible and convenient tool for the description of systems whose subsystems until primary (un-splitted) elements operate in parallel upon limited amounts of shared resources [Desrochers and Al-Jaar, 1995; Recalde et al., 2004].
A Petri net has nodes of two types – places and transitions – connected by directed arcs. Every arc connects a place with transition or transition with arc, so from the graph theory point of view PN is a bipartite directed graph. Each place at every moment contains a non-negative integer number of tokens. Marking of the net is defined as a vector whose elements are numbers of tokens having a place in the corresponding places. Marking defines the current state of a PN. A PN is transferred from one state to another by means of so called transitions firings, providing extraction of tokens from places being input for transition, and addition of tokens to places being output for transition. Transition fires only if there are tokens in all input places.
The closest model to the considered problem of STS sustainability assessment (let us be concerned only with the local case for simplicity) is the class of PN called colored timed Petri nets. Such PN have two main properties:
So, we may represent devices ("black boxes") entering a modeled technological base of STS by transitions, while the STS resource base is represented by a single place containing colored tokens, according to which, as noted above, we may represent amounts of specific resources. Operation of an STS is modeled by the operation of PN: all possible states of PN, that may be reached from the initial state corresponding to the initial resource base of STS, define states of STS RB that may be obtained by an STS technological base application via possible industrial production chains.
 |
| Figure 5 |
As it is shown at Figure 5, colored timed PN represents STS, explicated at Figure 2, in such a way, that it contains only two places and $K+1$ transitions. First of the places, marked by $I$, at the initial state contains $m_1 + \ldots + m_N$ tokens; $m_1$ tokens are colored by $a_1^{"}, \ldots, m_k$ tokens – by $a_k^{"}$ . Thus STS RB $I$ at the initial moment of STS operation is represented by this one place. Transitions $B_1,\ldots, B_K$ represent respective devices and have time marks, defining durations of operation cycles of these devices $(n_1 \cdot \Delta t, \ldots, n_k \cdot \Delta t)$. Transition $B$ represents order $q$ in such a way, that result of of its firing is occurrence of one token colored $q$ at place $G$. Number of tokens at place $G$ at the moment, when PN stops, defines number of various ways of order $q$ completion.
Impacts on the modeled STS may be easily represented by operations providing removal of tokens from the place, representing a resource base, and also another operation providing elimination of some transitions, representing affected devices. However, formulation of criteria of sustainability of the affected STS, defined by appropriate PN, is outside of the language and algorithmics of Petri nets.
As may be seen, Petri nets are a more precise and, from the substantive point of view, more adequate mathematical tool for STS modeling in comparison with various tools from the scheduling theory area. This is a consequence of a resource-driven approach to the manufacturing and logistics process representation. But at the same time Petri nets do not have tools for the description of orders, and PN algorithmics do not contain algorithms creating optimal (rational) schedules for completion of such orders.
Network models have been for a long time the most widely used tools for the formulation and solution of various transportation problems. The most often used application of networks and oriented graphs is representation of distributed infrastructures in such a way that nodes represent points (places) of various resources accumulation and use, while arcs represent links providing transportation of these resources between mentioned nodes. Arcs are usually marked by numbers defining length, bandwidth, traffic capacity and similar parameters of links, or, simply, time necessary for relocation of products (items) from one node to another. There are a lot of problems solved by application of this framework and known as the shortest path problem, the traveling salesman problem, the maximal flow problem, etc. [Ball et al., 1995; Jensen and Bard, 2003; Hillier and Lieberman, 2014; Miller, 2007]. Impacts on networks are represented simply by correction of parameters on arcs and/or elimination of nodes.
More complicated problems concerning optimal distribution of resources, optimal transportation of resources from places of their origination to places of their consumption, etc. are usually described by means of mathematical programming, first of all, linear programming (LP) and its multiple variations [Gartner and Matonsek, 2006; Miller, 2007; Roos et al., 2006; Vanderbei, 2001].
An LP problem is formulated usually in a vector-matrix basis in such a way, that it is necessary to find a vector $X_{(n)}= \| x_1 \ldots x_n \|$ of non-negative rational values that provide the maximal value of a linear function
\begin{eqnarray*} F(x) = \sum\limits_{i=1}^n c_i x_i \end{eqnarray*}under restrictions
\begin{eqnarray*} \sum\limits_{j=1}^n a_{ij} \cdot x_j \leq b_i \end{eqnarray*}where $ i= 1, \ldots, m$.
This basic scheme is the background for more sophisticated formulations involving some other restrictions, described by some additional mathematical tools [Vanderbei, 2001],
as well as multiple optimization functions providing formulation of a multicriteria optimization problem.
LP and its modifications for practical application is supported by widely and deeply developed efficient algorithmics, providing sufficiently fast search for optimal solutions on conventional and parallel computational hardware.
As is known, an LP toolkit may be used for description of some problems from the theory of scheduling [Artigues, 2012; Flondas and Lin, 2005].
Impacts in the LP formalization scheme may be represented by appropriate corrections of $c_i$, $b_j$ and $a_{ij}$ values; there are known approaches to minimization of computational complexity after correction of search for optimal solutions by the so-called "local correction" schemes [Sheremet, 1994].
Moreover, there are long-standing techniques of LP solution by representation of a concrete problem defined by a specific matrix $A$ and vectors $B$ and $C$ through the use of electric circuits [Dennis, 1959].
This approach provides search for an optimal solution as fast as a circuit containing analog elements (resistors and capacitors) will pass the transition process and enter the stable state corresponding to a solution. The same idea is in fact implemented in the up-to-date quantum computers, based on quantum annealing technology [Santoro and Tosatti, 2006].
Perhaps, the model closest to the considered STS problems is the LP model of the so-called production economy [Shoham and Leyton-Brown, 2009],
operating on the set of products and set of resources. Manufacturing of each product is based on the consumption of a certain amount of each resource, and each product is sold at a certain price. If we denote the amount of product $i$ as $x_i$, and its price as $c_i$, then the problem is to maximize profit
\begin{equation} \tag*{(1)} \sum\limits_{i=1}^n c_i x_i \end{equation}Denoting $a_{ij}$ as the amount of resource $j$ necessary for manufacturing of one unit of product $i$, and $b_j$ as the available amount of resource $j$, it is easy to formulate appropriate restrictions:
\begin{equation} \tag*{(2)} \sum\limits_{i=1}^n a_{ij} x_i \leq b_j \end{equation}As formulated, $B_{(m)}= \| b_1 \ldots b_m \|$ is a vector representation of the STS resource base, while $a_{ij}$ is input value of resource $j$ for "black box" $i$, and $C_{(n)}= \| c_1 \ldots c_n \|$ is a vector representation of order measured in the price units. The impact may be easily represented by vector $\Delta B$, subtracted from $B_{(m)}$, and sustainability of such a system may be defined as equality of solutions of (1)–(2) of the LP problem in both cases (with resource bases $B_{(m)}$ and $B_{(m)} - \Delta B$).
However, this model does not catch deep recursiveness, inherent to real manufacturing processes, where every manufacturing product may become a resource for manufacturing of other products and so on. As defined, (1)–(2) describe one-step manufacturing, in which no one "black box" output may serve as another "black box" input.
This disadvantage is inherent not only to this briefly described model of a production economy, but practically to all known matrix-vector-based economical models [Chiang and Wainwright, 2005; Samuelson, 1952],
thus underscoring insufficient flexibility and adequacy of classical matrix-vector-based mathematical toolkits for the considered bundle of the DSTS scheduling problems.
Along with the afore-mentioned, LP and mathematical programming as a whole have some more practical disadvantages, being the consequence of matrix-vector mathematical background: for practically valuable cases the dimension of matrices and vectors is so large that it is very difficult to prepare and maintain input data without errors. Another disadvantage of classical optimization approaches is that in many cases it is very difficult, if even possible, to formalize intuitively postulated conditions and criteria defining optimal solutions by matrix-vector multiplications and relations on the results.
That is why a serious research effort for the last decades was applied to the development of mathematical toolkits, incorporating some additional features for more convenient and precise formalization of systems analysis problems.
The practically most valuable results in this direction were obtained in the area of data and knowledge engineering – first of all, logic programming, deductive data bases and, perhaps the most valuable toolkit from this area – multiagent systems.
The kernel of the logic programming paradigm, implemented in a variety of dialects of the PROLOG programing language, is representation of a program, or a knowledge base (KB) as a set of the so called Horn clauses, each having the form
\begin{equation} \tag*{(3)} A_1, \ldots, A_m \to A_0 \end{equation}where $A_i$, $i=0, 1, \ldots, m$ are atomic constructions of the first order predicate calculus, called atoms, of the form $P (t_1, \ldots, t_l) : P$ is a predicate name, and $t_j$, $j= 1, \ldots, l$, are terms, being, in fact, functional expressions in prefix notation upon constants and variables [Gallaire et al., 1984; Kowalski, 1979].
The semantics of a PROLOG-like knowledge representation is based on the procedural interpretation of Horn clauses, the background for which is consideration of clause (3) as a procedure declaration with $A_0$ being head, while list $A_1, \ldots, A_m$ is the body of the procedure. A call of program (or query to the knowledge base) is a clause with empty head
\begin{eqnarray*} A \to \end{eqnarray*}The factual part of the knowledge base (or input data of the program) is a set of axioms, i.e., clauses with empty bodies
\begin{equation} \tag*{(4)} \to A_k \end{equation}where $k= 1, \ldots, K$, and $K$ is the total number of such axioms in the KB (program). The set of axioms (4) corresponds to the usual relational data base in such a way that
\begin{eqnarray*} \to R (a_1, \ldots, a_l) \end{eqnarray*}is equivalent to the tuple $ < a_1, \ldots, a_l > $ presence in the relation $R$.
The result of the program call (or of the query to the KB) is created by means of logical inference in the first order predicate logic whose kernel is so-called resolution, based, in turn, on the unification of atoms playing the role of the evaluation of variables during recursive top-down calls until terminating axioms. Because of the existential semantics of PROLOG, the consequence is that extraction of the only element of the possible non-empty set of solutions, involving integration of logic programming with data engineering mainstream (first of all, relational and post-relational data models), is rather difficult. (The same must be said about LoP application to the declared higher problems of STS analysis.)
Another approach to knowledge and data engineering integration was developed inside the so-called "deductive data bases" paradigm [Ceri et al., 1990; de Moor et al., 2011]. DDB is a relational data base with knowledge extension containing logical constructions similar to Horn clauses, but providing logical inference of new facts according to universal semantics; the background for this is semantics of the most widely used relational query language SQL [Date, 2009], which deductive extension is called Datalog. This approach as a whole creates some new features for primary consideration in the afore-mentioned problems, but there are no capabilities for the description of optimization criteria and restrictions, and, thus, for formulation and solution of STS optimization problems, as in higher mathematical programming, as well as for description of STS operation logic, similar to Petri nets.
Some new capabilities for these purposes are introduced by the so called "active data bases" (ADB) paradigm [Paton and Diaz, 1999].
Every ADB has knowledge extension through a set of "triggers" – procedures activated by the events of DB updates (deletion, insertion or replacement of DB elements) and, in turn, generating new updates. So, a wave of such recursively activated operations in the general case may represent a logical inference process as well as Petri net operation. ADB tools provide description of logics of maintenance of mutually interconnected elements of the stored data base and are widely used in the most powerful modern data base management systems, such as Oracle [Karam and Jones, 2014; Udayakumar, 2008], Sybase [Verschoor, 2012],
Informix [Grachov, 2000], MS SQL Server [Date, 2009], etc.
However, neither deductive nor active data bases provide direct and compact formulation and solution of the DSTS problems described in the first section of this paper. They are no more than a rather convenient framework for the development of software, implementing various algorithms for solution of the afore-mentioned problems.
Constraint programming, already mentioned earlier in connection with constraint-based scheduling, is another approach to transfer from procedural to declarative paradigm, whose main feature is the same as in PROLOG: Algorithm = Logic + Control [Kowalski, 1974].
There are a lot of examples illustrating the great usefulness of this approach, and one, concerning the area under consideration, was already considered in Section 3. Of course, CP is a highly interesting direction, and special argumentation of its applicability to DSTS scheduling and sustainability areas are redundant; however, the ideology, mathematics and algorithmics of such application must be worked out. One of the possible attempts to solve this problem is to use multiset grammars, considered below in Section 7.
Multiagent systems are a useful generalization of the knowledge engineering paradigms described earlier and are one of the most promising tools originating from the artificial intelligence area [Shoham and Leyton-Brown, 2009; Wooldridge, 2002].
Every MAS contains a finite number of agents, interacting by messages directly or via the so-called blackboard. Every agent operates according to his own logic of processing of the incoming messages. This framework provides a rather simple simulation of distributed social and economical systems behavior, as well as implementation of various heuristic optimization algorithms, such as auction-like optimization, contract nets, ant colonies etc. Also, there are known MAS implementing dynamic programming algorithms in application to the transportation problems from the operations research area, as well as MAS, providing solution of the assignment problem and the scheduling problem in their integer programming formulation.
It is quite evident, that MAS may be simply applied to the DSTS analysis problems, if to consider devices ("black boxes") as one type of agent, and order along with resource base as another. Interaction between agents is implemented by messages containing amounts of resources, which are used for new resource creation. In such a case, the problem is to develop algorithms for agents that provide creation of systems of contracts between agents for order completion. This system of contracts is, in fact, the DSTS schedule mentioned in the previous sections. However, logics and algorithms of MAS-based schedule generation must be worked out, and in such cases application of MAS ideology to the DSTS sustainability area forms no more than a basic computational environment or framework for this development. Another question is how to match MAS agents, as they were defined above, with real hardware and software used for DSTS scheduler operation. It is very interesting and promising that MAS ideology puts forward a decentralized approach to DSTS scheduling and rescheduling, which is based on the agents' interaction and doesn't use DSTS-S as a local operation center.
All we have said about possible MAS application to the considered bundle of DSTS scheduling problems leads us to the conclusion about usefulness of this direction, but also about essential research work that must be done for its realization.
The theory of recursive multisets (TRMS), which main content was presented in [Sheremet, 2010, 2011, 2018], is a result of an attempt to integration of the best features of classical optimization and modern knowledge engineering. Besides this abstract goal, there were also some practical aims, close to the listed DSTS-S design problems. That is why TRMS basic categories naturally fit the intermediate representation of DSTS described in Section 1.
A multiset (MS) differs from the classical set by presence of indistinguishable elements (objects), so a record
\begin{eqnarray*} \nu = \{ n_1 \cdot a_1 , \ldots, n_m \cdot a_m \} \end{eqnarray*}means multiset $\nu$ contains $n_1$ objects of type $a_1 , \ldots, n_m$ objects of type $a_m$ (each $n_i \cdot a_i$ is also called a multiobject, and $n_i$ the multiplicity). By this, the resource base of a DSTS may be represented as a multiset.
A multiset grammar is a couple $S= < \nu_0, R >$, where MS $\nu_0$ is called the kernel, and $R$ is the set of the so called rules
\begin{equation} \tag*{(5)} \nu \to \nu' \end{equation}where $\nu$ and $\nu'$ are multisets. MG $S$ generates a set of multisets by application of rules to already generated multisets, beginning from the kernel $\nu_0$. Application of rule (5) to multiset $\bar{\nu}$ is possible if $\nu$ is a submultiset of $\bar{\nu}$ (i.e., all objects entering $\nu$ enter $\bar{\nu}$), and results in replacement of $\nu$ by $\nu'$. A set of multisets generated by MG $S$ is denoted $V_S$, and the set of so called terminal multisets such that no one rule is applicable to them is denoted $\bar{V}_S$.
Returning to the intermediate representation of DSTS, it is quite natural to represent every device ("black box") by a rule, and the initial resource base by kernel $\nu_0$, so DSTS as a whole may be represented by a multigrammar $S= < \nu_0, R >$, where $R$ is the set of all mentioned rules (i.e., devices). As such, the operation of DSTS is fully represented by the generation of multisets by MG $S$, and every such multiset is the result of some manufacturing chain. Also, $\bar{V}_S$ is a set of such RB, which may be called the final resource base in the sense, that no one device can be applied to it because of lack of input resources necessary for its operation cycle.
An order, which was represented above as an additional "black box", may be also represented as an additional rule
\begin{equation} \tag*{(6)} \{ \bar{n}_1 \cdot \bar{a}_1 , \ldots, \bar{n}_l \cdot \bar{a}_l \} \to \{ 1 \cdot q \} \end{equation}where $\bar{n}_1 , \ldots, \bar{n}_l$ are amounts of objects (resources) $\bar{a}_1 , \ldots, \bar{a}_l$ that must be produced (manufactured) by DSTS; $q$ is an auxiliary object, denoting the name of the order. As may be seen, every multiset $\nu \in \bar{V}_S$ containing multiobject $1 \cdot q $ represents the possible result of order completion by one of the possible ways, and also the RB final state after this process terminates. If there is no set containing $1 \cdot q $, order $q$ cannot be completed by DSTS.
The impact on DSTS, whose technological base is represented by scheme $R$ of multigrammar $S= < \nu_0, R >$, may be easily represented by multiset $\Delta v$ containing amounts of resources, eliminated from the resource base by this impact, and set $\Delta R$, containing destroyed devices. So, there is a quite simple and evident criterion for the assessment of DSTS sustainability to the impact $< \Delta v, \Delta R >$ [Sheremet, 2016, 2018]: if
\begin{eqnarray*} (\exists \nu \in \bar{V}_{S^*}) 1 \cdot q \in \nu \end{eqnarray*}where $S^* = < \nu_0 - \Delta \nu, R - \Delta R >$, then DSTS is sustainable to the impact (i.e., there exists at least one way of order completion by the affected system).
The family of multiset grammars contains various classes of MG, describing various classes of DSTS and orders, while corresponding algorithms of generation of sets of multisets implement creation of schedules providing completion of those orders.
So, in alia, a filtering multigrammar $S =$ $< \nu_0, R, F >$ defines a set of terminal multisets as a subset of set $\bar{V}_{S}$ generated by MG $S' = < \nu_0, R >$; all elements of this subset satisfy filter $F$ containing so-called boundary and optimizing conditions, having the form $a\, \Theta\, n$ and $a=\,$opt respectively. Here $\Theta$ is a sign of a boundary condition $(\geq,\: = , \: \leq, \: > \: , <)$, opt $\in \{ \min, \max \}$ a sign of optimizing condition, while $a$ and $n$ are object name and number respectively. Filters provide selection of such TMS, which contain multiobjects with multiplicities, satisfying all conditions entering the filter. As can be seen, the language of filters is very close to the usual query languages, providing selection of elements from the relational and deductive databases by restrictions on values of attributes in these elements. Here every multiset $\{ n_1 \cdot a_1 , \ldots, n_m \cdot a_m \}$ is equivalent to the element $ < n_1 , \ldots, n_m > $ of the DB relation with attributes $ a_1 , \ldots, a_m $. The only difference from the DDB is that the set of multisets generated by MG $S' = < \nu_0, R >$ is in the general case infinite. However, optimizing conditions radically extend capabilities of this language, providing easy formulation of various optimization problems, and, what is very valuable, far beyond the classical scheme of linear programming.
Temporal multigrammars (TMG) provide description of manufacturing processes in connection with a unified scale of time, which creates background for formulation and solution of scheduling problems inside a multigrammatical framework. This feature is supported by rules like
\begin{eqnarray*} \{n_1 \cdot a_1 , \ldots, n_m \cdot a_m, n\cdot \Delta t \} \to \end{eqnarray*} \begin{eqnarray*} \{ n_1' \cdot a_1' , \ldots, n_l' \cdot a_l' \} \end{eqnarray*}where $\Delta t$ is an object representing time measurement unit, as was introduced earlier in Section 2; so multiobject $n \cdot \Delta t$ represents duration of the operation cycle of a device, that extracts $n_1$ objects $ a_1 , \ldots, n_m$ objects $a_m$, and after $n$ time units $\Delta t$ joins to RB $n_1'$ objects $ a_1', \ldots, n_l'$ objects $a_l'$. By including conditions like $t \stackrel{>}{<} \bar{n}$ or/and $t= \,$min to the filter $F$, which defines restrictions for order completion, one gives all the necessary input data for DSTS scheduling, which is implemented through the background of TMG generation algorithmics.
The general scheme of MG application as a tool for the solution of various problems of DSTS scheduling looks like the following. The knowledge base of DSTS-S is in fact scheme $R$, while the resource base of DSTS is kernel $\nu_0$ of the MG $S=<\nu_0, R>$ (in the general case $S$ is a temporal multigrammar). Every order to DSTS is a couple $< \nu, F >$, where
\begin{eqnarray*} \nu = \{ \bar{n}_1 \cdot \bar{a}_1 , \ldots, \bar{n}_l \cdot \bar{a}_l \} \end{eqnarray*}is the left part of rule (6), and $F$ is the filter, containing conditions for filtering resource bases, that would be obtained after order completion. These variants are filtered, in fact, by filter $F \cup \{ q=1 \}$, and, if there is more than one variant, the scheduler selects one of them arbitrarily, or suggests DSTS management to perform further actions (for example, filtration of a set of variants by the additional filter $F'$). The flow of the orders is processed with a maximal degree of parallelism, i.e., processing of every next order starts immediately, no matter how many previous orders are being processed at this moment. If impacts occur while orders are being completed, rescheduling is performed upon corrected KB and RB.
Multiset grammars look like one of the most promising tools for the DSTS problem solution. The MG current state of the art, however, is not yet sufficient for their broad implementation, that is why a strong research effort must be applied to this approach for further development.
Comparison of capabilities of the considered mathematical toolkits for DSTS scheduling problems leads us to the conclusion that there are two most promising families of such tools – multiagent systems and multiset grammars, whose development and, perhaps, integration will be the most successful approach to the considered area. This approach would be supported, however, by cooperation of multiple research groups from different countries. Such cooperation may be implemented by some authoritative international think-tanks like CODATA (the Committee on Data of the International Council for Science) or IIASA (International Institute for Applied Systems Analysis).
The authors would be glad to participate in such collaboration.
| ADB | active data base |
| CBS | constraint-based scheduling |
| CP | constraint programming |
| DB | data base |
| DDB | deductive data base |
| DE | digital economy |
| DSTS | distributed sociotechnical system |
| DSTS-S | DSTS scheduler |
| IoT | Internet of Things |
| KB | knowledge base |
| LP | linear programming |
| LoP | logic programming |
| MAS | multiagent system |
| MG | multiset grammar (multigrammar) |
| MS | multiset |
| ND | natural disaster |
| PJSSP | Preemptive Job-Shop Scheduling Problem |
| PN | Petri net |
| RB | resource base |
| RCPSP | Resource Constrained Project Scheduling Problem |
| RR | reusable resource |
| STS | sociotechnical system |
| STS-S | STS scheduler |
| TB | technological base |
| TMG | temporal multiset grammar |
| TRMS | theory of recursive multisets |
| WAN | wide area network |
Adams, W. M., S. J. Jeanrenand (2013), Transition to Sustainability: Towards a Human and Diverse World, 108 pp., International Union for Conservation of Nature and Natural Resources (IUCN), Gland, Switzerland.
Artigues, C. (2012), Scheduling and (Integer) Linear Programming, 168 pp., LAAS-CRNS & Universite de Toulouse, Toulouse.
Bakari, M. E.-K. (2017), The Dilemma of Sustainability in the Age of Globalization: A Quest for a Paradigm of Development, Lexington Books, NY.
Baker, K. R., D. Trietsch (2009), Principles of Sequencing and Scheduling, John Wiley & Sons, Hoboken, New Jersey.
Ball, M., T. Magnanti, B. Monma, G. L. Niemhauser (eds.) (1995), Network Models. Handbook in Operations Research and Management Science, Vol. 7, 798 pp., Elsevier Science, Amsterdam.
Baptiste, Ph., C. Le Pape, W. Nuijten (2001), Constraint-Based Scheduling: plying Constraint Programming to Scheduling Problems, 198 pp., Springer, Berlin, Heidelberg.
Black, I. R., H. Cherrier (2010), Anti-consumption as part of living a sustainable lifestyle: Daily practices, contextual motivations and subjective values, Journal of Consumer Behavior, 9, no. 6, p. 437, https://doi.org/10.1002/cb.337.
Brucker, P. (2001), Scheduling Algorithms, 365 pp., Springer-Verlag, Berlin.
Ceri, S., G. Gottlob, L. Tanca (1990), Logic Programming and Databases, 280 pp., Springer-Verlag, Berlin, https://doi.org/10.1007/978-3-642-83952-8.
Chatfield, C., T. Johnson (2013), Microsoft Project 2013 Step by Step, 576 pp., Microsoft Press, Indianapolis.
Chiang, A. C., K. Wainwright (2005), Fundament Methods of Mathematical Economics, 700 pp., McGraw-Hill, New York.
Date, C. J. (2009), SQL and Relational Theory. How to Write Accurate SQL Code, 474 pp., O'Reilly, Sebastopol, CA.
De Moor, O. (eds.), et al. (2011), Datalog Reloaded, Lecture Notes in Computer Science, Vol. 6702, p. 407, Springer, Berlin–Heidelberg.
Dennis, J. B. (1959), Mathematical Programming and Electrical Networks, 186 pp., MIT, Cambridge, MA.
Desrochers, A. A., R. Y. Al-Jaar (1995), Applications of Petri Nets in Manufacturing Systems: Modeling, Control, and Performance Analysis, IEEE Press, NY.
Dubois, J., A. Gvishiani (1998), Dynamic Systems and Dynamic Classification Problems in Geophysical plications, 256 pp., Springer-Verlag, Paris, https://doi.org/10.1007/978-3-642-49951-7.
Flondas, C., X. Lin (2005), Mixed Integer Linear Programming in Process Scheduling: Modeling, Algorithms, and Applications, Annals of Operations Research, 139, p. 131–162.
Gallaire, H., J. Minker, J.-M. Nicolas (1984), Logic and Databases: A Deductive Approach, ACM Computing Surveys, 16, no. 2, p. 153–185, https://doi.org/10.1145/356924.356929.
Gartner, B., J. Matonsek (2006), Understanding and Using Linear Programming, Springer, Berlin.
Geissdoerfer, M., P. Savaget, N. M. P. Bocken, E. J. Hultink (2017), The Circular Economy – A New Sustainability Paradigm, Journal of Cleaner Production, 143, p. 757–768, https://doi.org/10.1016/j.jclepro.2016.12.048.
Grachov, A. Yu. (2000), Introduction to Informix DBMS, Dialog-MEPHI, Moscow (in Russian).
Gvishiani, A., J. Dubois (2002), Artificial Intelligence and Dynamic Systems for Geophysical Applications, 350 pp., Springer-Verlag, Paris, https://doi.org/10.1007/978-3-662-04933-4.
Gvishiani, A. D., S. M. Agayan, Sh. R. Bogoutdinov (2008), Fuzzy recognition of anomalies in time series, Doklady Earth Sciences, 421, no. 1, p. 838–842, https://doi.org/10.1134/S1028334X08050292.
Gvishiani, A., et al. (2014), Survey of Geomagnetic Observations Made in the Northern Sector of Russia and New Methods for Analysing Them, Surveys in Geophysics, 35, no. 5, p. 1123–1154, https://doi.org/10.1007/s10712-014-9297-8.
Gvishiani, A., et al. (2016), Automated Hardware and Software System for Monitoring the Earth's Magnetic Environment, Data Science Journal, 15, p. 18, https://doi.org/10.5334/dsj-2016-018.
Hermann, M., T. Pentek, B. Otto (2016), Design Principles for Industrie 4.0 Scenarios, 2016 49th Hawaii International Conference on System Sciences, HICSS, Hawaii, https://doi.org/10.1109/HICSS.2016.488.
Hillier, F. S., G. J. Lieberman (2014), Introduction to Operations Research, McGraw-Hill, Boston, MA.
Huws, U. (2015), Capitalism and the Cybertariat – Contradictions of the Digital Economy, Monthly Review, 66, no. 8, p. (January 2015).
Jensen, P. A., J. F. Bard (2003), Operations Research Models and Methods, 623 pp., John Wiley & Sons, New York.
Karam, S., B. Jones (2014), Oracle Grid and Real Application Clusters: Oracle Grid Computing with RAC, 214 pp., TechPress, Rampant.
Kowalski, R. (1974), Predicate Logic as Programming Language, Information Proceedings 74, p. 569–574, North Holland Publishing Company, Amsterdam.
Kowalski, R. A. (1979), Algorithm = Logic + Control, Communications of the ACM, 22, no. 7, p. 424–436, https://doi.org/10.1145/359131.359136.
Le Billon, P. (ed.) (2005), The Geopolitics of Resources Wars. Resource Dependence, Governance and Violence, 277 pp., Routledge Taylor & Francis, London–New York.
Miller, S. (2007), An Introduction to Linear Programming, 28 pp., Brown University, Brown.
The New Digital Economy:, (2011), How it Will Transform Business, 31 pp., Economics, Oxford.
Paton, N. W., O. Diaz (1999), Active Database Systems, ACM Computing Surveys, 31, p. 1–47, https://doi.org/10.1145/311531.311623.
Pearce, J. M. (2012), The Case for Open Source Appropriate Technology, Environment, Development and Sustainability, 14, no. 3, p. 425–431, https://doi.org/10.1007/s10668-012-9337-9.
Pegden, C. D. (2009), Intelligent Objects: The Future of Simulation, 7 pp., LLC, Simio.
Pinedo, M. L. (2008), Scheduling Theory, Algorithms, and Systems, 671 pp., Springer, Berlin.
Roberts, F. S. (1982), Planning for energy disruptions, Energy Modeling IV: Planning for Energy Disruptions, p. 1–13, Inst. of Gas Tech., Chicago.
Recalde, R., M. Silva, J. Ezpeleta, E. Teruel (2004), Petri Nets and Manufacturing Systems: An Examples-Driven Tour, 47 pp., Universidad de Zaragoza, Zaragoza.
Roberts, F. S. (2011), The port reopening scheduling problem, H. Kaul and H. M. Mulder (eds.), Advances in Interdisciplinary Applied Discrete Mathematics. Interconnections between Consensus and Voting Theory, Clustering, Location Theory, Mathematical Biology, and Optimization, Vol. 11, p. 199–210, World Scientific, Singapore.
Roos, C., T. Terlaky, J.-P. Vial (2006), Understanding and Using Linear Programming, Springer, Berlin.
Samuelson, P. A. (1952), Economic Theory and Mathematics – An Appraisal, American Economic Review, 42, no. 2, p. 56–65.
Santoro, G. E., E. Tosatti (2006), Optimization Using Quantum Mechanics: Quantum Annealing Through Adiabatic Evolution, Journal of Physics A: Mathematical and General, 39, no. 36, p. R 393.
Sheker, R. R. (2015), The Spatial Distribution of Development in Europe and its Underlying Sustainability Correlations, Applied Geography, 63, p. 304–314, https://doi.org/10.1016/j.apgeog.2015.07.009.
Sheremet, I. A. (1994), Intelligent Software Environments for Automated Information Processing Systems, 544 pp., Nauka, Moscow (in Russian).
Sheremet, I. A. (2010), Recursive Multisets and Their Applications, 293 pp., Nauka, Moscow (in Russian).
Sheremet, I. A. (2011), Recursive Multisets and Their Applications, 249 pp., NG Verlag, Berlin.
Sheremet, I. A. (2016), Multiset Approach to the Estimation of Consequences of Natural Disasters Impacts on Industrial Systems, Geoinformatics Research Papers, 4, p. BS4002, https://doi.org/10.2205/2016BS01Sochi.
Sheremet, I. A. (2018), Multiset Analysis of Consequences of Natural Disasters Impacts on Large-Scale Industrial Systems, Data Science Journal, 17, no. 4, p. 1–17, https://doi.org/10.5334/dsj-2018-004.
Shoham, Y., K. Leyton-Brown (2009), Multiagent Systems. Algorithmic, Game – Theoretic, and Logical Foundations, 532 pp., Cambridge University Press, Cambridge, UK.
Tapscoft, D. (1997), The Digital Economy: Promise and ril e e of tworked telligence, McGraw-Hill, NY.
Udayakumar, K. (2008), Oracle SOA Patterns: Demystify Service Design and Implementation Patterns in Oracle SOA Suite, 388 pp., Bloomington, Indiana, Trafford Publishing.
Ustundag, A., E. Cevicsan (2017), Industry 4.0: Managing the Digital Transformation, Springer, Berlin.
Vanderbei, R. (2001), Linear Programming: Foundations and Extensions, Springer-Verlag, Berlin.
Verschoor, R. (2012), The Complete ASE Quick Reference Guides. 6th Edition, 150 pp., Sypron B. V., Amersfoort, NL.
Waite, M. (2013), SURF Framework for a Sustainable Economy, Journal of Management and Sustainability, 3, no. 4, p. 25–40.
Wooldridge, M. (2002), An Introduction to Multiagent Systems, 368 pp., John Wiley & Sons, New York.
Wright, R. (2004), A Short History of Progress, 208 pp., House of Anansi Press, Toronto.
Received 14 March 2018; accepted 29 June 2018; published 21 August 2018.


Citation: Gvishiani A. D., F. S. Roberts, I. A. Sheremet (2018), On the assessment of sustainability of distributed sociotechnical systems to natural disasters, Russ. J. Earth Sci., 18, ES4004, doi:10.2205/2018ES000627.
Copyright 2018 by the Geophysical Center RAS.