
RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 18, ES4003, doi:10.2205/2018ES000626, 2018
A. Soloviev1,2, Sh. Bogoutdinov1,2, S. Agayan1, R. Redmon3, T. M. Loto'aniu3,4, H. J. Singer5
1Geophysical Center of the Russian Academy of Sciences (GC RAS), Moscow, Russia
2Schmidt Institute of Physics of the Earth of the Russian Academy of Sciences (IPE RAS), Moscow, Russia
3National Oceanic and Atmospheric Administration National Centers for Environmental Information, Boulder, CO, USA
4Cooperative Institute for Research in Environmental Sciences, University of Colorado, Boulder, CO, USA
5National Oceanic and Atmospheric Administration Space Weather Prediction Center, Boulder, CO, USA
As a part of the space environment monitor instrument suite, Geostationary Operational Environmental Satellite carries two boom-mounted magnetometers that measure the local magnetic field vector with a 0.5 second sampling rate. These data contain occasional baseline perturbations not of geophysical origin. One source of contamination is due to switching heaters that are installed along with each magnetometer and used to stabilize the temperature of the instrument. Detection of the heater induced field is complicated by the fact that in most cases these jumps are so small that they are hard to distinguish visually. In the present work we have developed the algorithm JM (from JUMP) aimed at automated and uniform recognition of jumps in GOES 2 Hz vector magnetic measurements. We present the performance of the JM algorithm to a full day of measurements on 3 April 2010. On this date, almost all jumps were recognized by the JM algorithm. The results demonstrate that the algorithm might be used to improve the existing data set from GOES 13, 14 and 15 series, and perhaps find use with the next generation of GOES satellites, beginning with GOES 16 launched on 19 November 2016.
Over the last decades, the number and size of geophysical digital data sets have been rapidly increasing due to the expanding use of satellites and ground-based observational networks and an increase in sampling rate. Consequently, the role for automated tools for data handling and intellectual analysis is becoming more crucial. An expert is can deal easily with small amounts of data to extract useful information about geophysical phenomena; however, as data volumes increase, it becomes impossible to mine efficiently desired information, and other particularities, without adequate automated methods for big data analysis. Therefore, useful knowledge extraction needs to be formalized in an objective and uniform process.
Many geophysical studies rely on the analysis of observed time-dependent parameters in the form of one- or multidimensional time series. In geomagnetism, a prime source of information about the evolution of Earth's magnetic field are continuous recordings of the magnetic field components made by ground-based observatories [Love and Chulliat, 2013] and low-orbit satellites [Friis-Christensen et al., 2006]. Currently there are more than 200 stations and observatories operating worldwide, providing real-time data on Earth's magnetic field sampled every second, and even more frequently. Taking into account a great variety of spectral-temporal characteristics of the physical signals under consideration, it is crucial to have geomagnetic data corrected for any instrumental or non-natural disturbances in a timely manner. Automated data processing for man-made/natural classification of anomalies is a non-trivial problem, attaining a classical status. This is one of the reasons, why at many worldwide observatories such filtering is still carried out manually [Reda et al., 2011; Zhang et al., 2016], which in turn leads to long time delay in preparation of verified data.
Probabilistic-statistical methods for detecting disturbances in magnetic records, such as frequency-time analysis [e.g., Balasis et al., 2013], wavelet analysis [e.g., Mandrikova et al., 2013] and neural networks [e.g., Ouadfeul et al., 2015] are effective in the presence of a priori information. In many cases, a priori information about the disturbances under consideration is very limited and concerns only some basic ideas about observed conditions and patterns. The shape of the anomaly is a rather fuzzy concept, and its correlation properties are unknown. Since the nature of the phenomena reflected in the recorded data is a priori not known, and variable in time, the methods for their detection need to be highly adaptive. We need methods of time series analysis that will allow solving anomaly recognition problems in the most general case.
For many years, we've been developing a general mathematical theory "Discrete Mathematical Analysis (DMA)" [e.g., Agayan et al., 2016, 2018] and a set of methods based on it for the recognition of anomalies in various geophysical observations [Gvishiani et al., 2014; Kulchinsky et al., 2010; Soloviev et al., 2012a, 2012b, 2013, 2016; Zlotnicki et al., 2005]. The creation of a common formalized methodology ensures the independence of results of processing from subjective factors (e.g., differences in the approaches of different experts to the data analysis).
In this paper, we apply the DMA approach to the detection of non-natural, instrumentally induced jumps in geomagnetic recordings. One of the main reasons for the baseline jumps in magnetograms is a sharp temperature change in the vicinity of the vector magnetometer (for example, in the observatory pavilion). Temperature variations are also the reason for the baseline drifts in some modern ground-based magnetometers that are characterized by a value of around 0.1–0.5 nT/° C. Drifts might be long-term of more than 2 nT per year.
 |
| Figure 1 |
The informal logic underlying jump detection is expressed in the following way: "A jump is an anomaly on a record leading to its baseline shift." We call the algorithm JM, reflecting its task. An essential element of the algorithm is the fuzzy measure of jumpiness, demonstrated in Figure 1. It is derived from the original time series and defined in the same domain (registration period) as a functional ranging between 0 and 1. Higher values correspond to baseline shifts in the primary record. This functional is defined using fuzzy comparisons, described in [Gvishiani et al., 2008a, 2008b, 2014].
We interpret a record (magnetogram) as a time series $y=\{y_t = y(t)\}$, defined in the interval (registration period) $T$ on the discrete semiaxis ${\mathbb R}_h^+ = \{t= kh, \; h > 0 , k= 1, \, 2, \ldots \}$, where $h$ is the discretization step and $k$ is the observation node. Without loss of generality we assume $h=1$.
The algorithm relies on the so-called fuzzy margins, which we define below. Basically they reflect a typical range of variation of an arbitrary numerical set. Let $A = \{a_i\} |_1^n$ be a finite numerical set and $B\subseteq A$ is its arbitrary subset. Then $|B|$ is an order of this subset, $\sum B = \sum b$: $b \in B$ is a sum of its elements and $S(B) = \sum B / |B|$ is their average. Fuzzy iterational upper and lower scalar margins $S^+ (A)$ and $S^- (A)$ are defined for $A$ inductively with the use of the intermediary subsets $A_k^+$, $A_k^-$.
At the beginning of induction, for $k=0$ we assume
\begin{eqnarray*} S_0^+ (A) = S_0^- (A) = S (A) \end{eqnarray*} \begin{eqnarray*} A_0^+ = \{ a \in A: a \geq S_0^+ (A) \} \end{eqnarray*} \begin{eqnarray*} A_0^- = \{ a \in A: a \leq S_0^- (A) \} \end{eqnarray*}If margins $S_k^+ (A)$, $S_k^- (A)$ and the sets $A_k^+$, $A_k^-$ are already defined, we assume
\begin{eqnarray*} S_{k+1}^+ (A) = \frac{\sum A_k^+ - |A_k^+| \cdot S_{k}^+ (A)}{|A|} + S_{k}^+ (A) \end{eqnarray*} \begin{eqnarray*} S_{k+1}^- (A) = \frac{\sum A_k^- - |A_k^-| \cdot S_{k}^- (A)}{|A|} + S_{k}^- (A) \end{eqnarray*} \begin{eqnarray*} A_{k+1}^+ = \{ a \in A: a \geq S_{k+1}^+ (A) \} \end{eqnarray*} \begin{eqnarray*} A_{k+1}^- = \{ a \in A: a \leq S_{k+1}^- (A) \} \end{eqnarray*}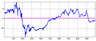 |
| Figure 2 |
As fuzzy upper and lower margins $\overline{\mathrm{sup}} A$ and $\overline{\mathrm{inf}} A$ for $A$ we select $S_k^+$ and $S_k^-$ for the given order $k$. Figure 2 illustrates fuzzy margins calculated for the orders from 0 to 5 for the specified time series.
Fuzzy bounds partition number scale $\mathbb{R}$ with respect to $A$ with different rigidity degree into four segments: small, insignificantly small, insignificantly large, large. The higher $k$, the partition is more rigid and the specificity of $A$ is less taken into account.
| $S_k$ small (significant) | $(- \infty, S_k^- (A)]$ | ||
| $W_k$ small (insignificant) | $(S_k^- (A), S_0 (A)]$ | ||
| $P \in \mathbb{R}$ | $W_k$ large (insignificant) | $ \quad \mathrm{modulus} A\Leftrightarrow p \in \quad $ | $(S_0, S_k^+ (A)]$ |
| $S_k$ large (significant)} | $(S_k^+ (A), + \infty]$ |
Extremely rigid partition is gained with $k= \infty$, assumed that $S_k^- =\,$min$\,A$, $S_k^+ =\,$max$\,A$:
| $S_{\infty}$ small | $(- \infty, \min A]$ | ||
| $W_{\infty}$ small | $(\min A, S_0]$ | ||
| $P \in \mathbb{R}$ | $W_{\infty}$ large | $ \quad \mathrm{modulus} A\Leftrightarrow p \in \quad $ | $(S_0, \max A]$ |
| $S_{\infty}$ large | $(\max A, + \infty]$ |
The difference $W_k(A) = S_k^+(A) - S_k^-(A)$ might be naturally referred as stochastic width of $A$ of the $k$-th order. $W_k(A)$ flexibly reflects traditional standard deviation $\sigma(A) = \sqrt{d(A)}$.
 |
| Figure 3 |
Now we can proceed to detection of jumps using FCARS (Fuzzy Comparison Algorithm for Recognition of Signals) [Gvishiani et al., 2008a, 2008b] and the methodology of the fuzzy margin calculation. Since jumps are treated as anomalies (see informal logic), we apply the FCARS algorithm to recognition of all anomalies (time disturbances) on a record $y(t)$. Let $A= y|_{[c,d]}$ be an arbitrary anomaly on $y(t)$, recognized by FCARS algorithm (Figure 3). Hence, the supposed jump in anomaly $A$ on $y(t)$ has to lead to a significant shift of a record level in the vicinity of $A$. Therefore, by choosing the observation parameter $\Lambda \in \mathbb{R}_h^+$ we turn from the anomaly $A$ to its $\Lambda$-neighborhood: $A(\Lambda) = y|_{[c-\Lambda, d+\Lambda]}$. We then proceed to detection of jump $j (A) = [a,b]$ on the interval $[c,d]$ for $A(\Lambda)$. Its detection is carried out using the calculation of fuzzy margins of a finite numerical set: fuzzy supremum $\overline{\mathrm{sup}}$ and fuzzy infimum $\overline{\mathrm{inf}}$ (their definition is given above).
For each interval $[\bar{a}, \bar{b}] \subseteq [c,d]$ we define soft corridors using fuzzy margins, which the fragments $y|_{[\bar{a}-\Lambda, \bar{a}]}$ and $y|_{[\bar{b}, \bar{b} + \Lambda]}$ fit. From the left side we denote their lower and upper borders as linf$ \; y [\bar{a}, \bar{b}]$ and lsup$ \; y [\bar{a}, \bar{b}]$, respectively, and from the right side as rinf$ \; y [\bar{a}, \bar{b}]$ and rsup$ \; y [\bar{a}, \bar{b}]$, respectively:
\begin{eqnarray*} \mathrm{linf} \: y [\bar{a}, \bar{b}] = \overline{\mathrm{inf}} \{ y(t): t \in [\bar{a}-\Lambda, \bar{a}]\} \end{eqnarray*} \begin{eqnarray*} \mathrm{lsup} \: y [\bar{a}, \bar{b}] = \overline{\mathrm{sup}} \{ y(t): t \in [\bar{a}-\Lambda, \bar{a}]\} \end{eqnarray*} \begin{eqnarray*} \mathrm{rinf} \: y [\bar{a}, \bar{b}] = \overline{\mathrm{inf}} \{ y(t): t \in [\bar{b}, \bar{b} +\Lambda]\} \end{eqnarray*} \begin{eqnarray*} \mathrm{rsup} \: y [\bar{a}, \bar{b}] = \overline{\mathrm{sup}} \{ y(t): t \in [\bar{b}, \bar{b} +\Lambda]\} \end{eqnarray*}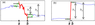 |
| Figure 4 |
If the interval $[\bar{a}, \bar{b}]$ is a jump then constructed $\Lambda$-corridors of the record $y(t)$ to the left and to the right from the interval $[{a}, {b}]$ have to be located at significantly different levels. This leads to two successive tests that we denote $T_1$ and $T_2$ (Figure 4). The first test $T_1$ is fulfilled if
\begin{eqnarray*} T_{1, \mu} : \mathrm{linf} \, y [\bar{a}, \bar{b}] \leq \mathrm{lsup} \, y [\bar{a}, \bar{b}] < \mathrm{rinf} \, y [\bar{a}, \bar{b}] \leq \end{eqnarray*} \begin{eqnarray*} \mathrm{rsup} \, y [\bar{a}, \bar{b}] \; \mathrm{(jump \; up)} \end{eqnarray*}or
\begin{eqnarray*} T_{1, d} : \mathrm{lsup} \, y [\bar{a}, \bar{b}] \geq \mathrm{linf} \, y [\bar{a}, \bar{b}] > \mathrm{rsup} \, y [\bar{a}, \bar{b}] \geq \end{eqnarray*} \begin{eqnarray*} \mathrm{rinf} \, y [\bar{a}, \bar{b}] \; \mathrm{(jump \; down)} \end{eqnarray*}Let us agree that the record $[\bar{a}, \bar{b}] \subset T_1$ signifies feasibility of the test $T_1$ for the interval $[\bar{a}, \bar{b}]$. For $[\bar{a}, \bar{b}] \subset T_1$ we define the measure of jumpiness $jmes A [\bar{a}, \bar{b}]$ of the anomaly $A$ on the interval $[\bar{a}, \bar{b}] \subseteq [c,d]$ using fuzzy comparison of inner and outer distances $h_1$ and $h_2$ (see Figure 4):
\begin{eqnarray*} jmes A [\bar{a}, \bar{b}] = n(h_1, h_2) \end{eqnarray*}where
\begin{eqnarray*} h_1= \left\{ \begin{array}{l} \mathrm{rinf} \, y [\bar{a}, \bar{b}] - \mathrm{lsup} \, y [\bar{a}, \bar{b}] \mathrm{linf} \, y [\bar{a}, \bar{b}] - \mathrm{rsup} \, y [\bar{a}, \bar{b}] \end{array} \right. \end{eqnarray*} \begin{eqnarray*} h_2= \left\{ \begin{array}{l} \mathrm{rsup} \, y [\bar{a}, \bar{b}] - \mathrm{linf} \, y [\bar{a}, \bar{b}] \mathrm{lsup} \, y [\bar{a}, \bar{b}] - \mathrm{rinf} \, y [\bar{a}, \bar{b}] \end{array} \right. \end{eqnarray*} \begin{eqnarray*} [\bar{a}, \bar{b}] \in \left\{ \begin{array}{l} T_{1, \mu} T_{1, d} \end{array} \right. \end{eqnarray*}and $n()$ is a fuzzy comparison (see [Gvishiani et al., 2008a, 2008b, 2014])."
The measure $jmes$ enables further test of the anomaly $A$ for the jump presence in it: we consider that the anomaly $A=y|_{[\bar{a}, \bar{b}]}$ on the fragment $[\bar{a}, \bar{b}]\subseteq [c,d]$ undergoes a jump, if the test $T_2$ is valid:
\begin{eqnarray*} T_2 : jmes A [\bar{a}, \bar{b}] < \beta \end{eqnarray*}If the anomaly $A=y|_{[c,d]}$ satisfies the tests $T_1$ and $T_2$, as its jump $j(A)$ we consider the fragment $[a,b]\subseteq [c,d]$, for which the measure $jmes A [\bar{a}, \bar{b}]$ is minimal:
\begin{eqnarray*} \begin{array}{ccc} j(A) \stackrel{def}{=} [a,b] = & \stackrel{\displaystyle{\mathrm{argmin}}}{_{[\bar{a}, \bar{b}] \in (T_1\wedge T_2)}} & jmes A [\bar{a}, \bar{b}] \end{array} \end{eqnarray*}The tests $T_1$ and $T_2$ will not change, if the fragment $A(\Lambda) = y|_{[c -\Lambda, d+\Lambda]}$ is replaced with the multiple fragment $\lambda A(\Lambda) = \lambda y|_{[c -\Lambda, d+\Lambda]}$ for $\lambda > 0$. In other words, the tests $T_1$ and $T_2$ are uniform. This is the consequence of the uniformity of the constructions $\overline{\mathrm{inf}} (\;)$, $\overline{\mathrm{sup}} (\;)$ and fuzzy comparison $n (\;)$. Therefore the jumps on a record $y(t)$ satisfying the tests $T_1$ and $T_2$ might have insignificant absolute magnitude. The example in the Figure 4a illustrates that: the anomaly recognized by the FCARS algorithm leads to insignificant level shift.
Thus, we need one more test of the potential jump for its absolute magnitude. Its logic is the following: if the anomaly $A$ contains a jump $j(A) = [a,b]$, then after its removal from the record $y(t)$ a new record $\tilde{y}(t) = y(t) - y|_{[a,b]}$ should also undergo a jump in the newly neighboring points $a-h$ and $b+h$, in particular, these points will be classified as anomalous by the FCARS algorithm. We proceed to the test $T_3$, based on the FCARS algorithm:
\begin{eqnarray*} T_{3} : \mathrm{min}(F_{\tilde{y}} (a-h|\Delta), \; F_{\tilde{y}}(b+h|\Delta)) \geq \alpha_s \end{eqnarray*}$F_{\tilde{y}} (\cdot |\Delta)$ is a rectification of the record $\tilde{y}$ based on the local observation $\Delta \in \mathbb{R}_h^+$, $\Delta < \Lambda$, $\alpha_s$ is the anomalousness level in the FCARS algorithm.
Successive implementation of the steps described above provides the objective recognition of jumps on a time series $y(t)$ and represents a self-sufficient algorithm for their search. The specific implementation of the JM algorithm is defined by choice of the following free parameters:
 |
| Figure 5 |
The US National Oceanic and Atmospheric Administration (NOAA) Geostationary Operational Environmental Satellite (GOES) constellation provides information on the state of the geospace Earth environment from Earth's atmosphere to the magnetosphere. The measured characteristics are used by NOAA's National Weather Service for short-term weather and space weather forecasting, and the data are further distributed by the US National Environmental Satellite, Data, and Information Service to a broad community including various research and commercial centers, universities, US and international space weather partners. GOES travel in a geosynchronous orbit around Earth with the same speed as Earth's rotation, which makes it possible to carry out continuous observations of the same area on Earth's surface. At an altitude of 35,800 kilometers above Earth in the equatorial plane, GOES 13 and GOES 15 satellites provide information about Earth's surface and near-Earth space. The monitoring coverage is shown in Figure 5: GOES 13 is located at 75° W and covers North and South Americas, and most of the Atlantic Ocean; GOES 15 is located at 135° W and monitors North America and Pacific Ocean. The two operate together to produce a full-face picture of the Earth, day and night.
Along with meteorological measurements, GOES satellites sample the Earth's magnetic field [Singer et al., 1996]. These measurements represent three orthogonal component variations, recorded by two vector magnetometers with 2 Hz frequency. The magnetic field recordings are burdened with numerous baseline jumps. Mainly those (but not all) are due to automatic switches of the heater systems, which are paired with each magnetometer. Hence, a problem of the satellite data filtering is broadly connected with baseline jump removal. The situation is complicated by the fact that in most cases, the jumps are so small that it becomes very difficult to recognize them visually. For this purpose, we apply the JM algorithm, which enables automatically and uniformly recognize jumps in GOES magnetograms.
 |
| Figure 6 |
The algorithm validation was carried out using daily magnetograms of the three magnetic field components ($B_x$, $B_y$, $B_z$), recorded by GOES 15 satellite on 3 April 2010. The supplementary information includes time series with a 5-min sampling rate reflecting the status of two heaters paired with a magnetometer. The status values are 0 (both heaters are off), 1 (1-st heater is on), 2 (2-nd heater is on) and 3 (both heaters are on) (Figure 6).
For each component, we empirically defined the same set of the free parameter values of the algorithm: $\Delta=5$, $\Lambda=60$, $\alpha=0.9$, $\beta=0.5$. Of course, the recognition results depend on the choice of the free parameter values. Therefore, they will have to be carefully adjusted for effective processing of the new generation GOES 16 data, in particular having different sampling rate (10 Hz).
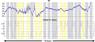 |
| Figure 7 |
 |
| Figure 8 |
As a result of the visual inspection it was concluded that almost all jumps were recognized by the JM algorithm in magnetograms recorded on 3 April 2010. Notably, most of the jumps are hardly detectable by eye, as it is shown in Figure 7–Figure 8. They are typically less than 1 nT. Each of the figures contains fragments of the original magnetic record and corresponding heater status plot. It is worth mentioning that, in addition to a clear dependency of jumps on heater switches, some cases demonstrate only a partial correlation, i.e. either heater switches are not producing jumps (Figure 7) or jumps occurred during constant heater status (Figure 8). Some of these situations arise from incomplete heater status monitoring and the lack of high-data rate heater status.
 |
| Figure 9 |
Separate and combined analysis of each component record led to the following additional conclusions, illustrated in Figure 9:
 |
| Table 1 |
A more detailed statistics on the recognition results is given in Table 1. Unfortunately, we could not quantitatively estimate the recognition results in terms of target misses and false alarms by comparing them with manually filtered and adjusted magnetograms, as the latter was not carried out.
Detection of anthropogenic jumps in geomagnetic records by using simple algorithms, e.g. based on threshold exceedance of time derivatives, is not valid – such disturbances, as anthropogenic spikes or geomagnetic pulsations (= two consecutive jumps of a different sign), as well as high amplitude rapid variations during magnetic storms are also characterized by large derivatives. The difficulty of detecting jumps is, in particular, in additional estimation of the shift in the recording level. Herein, we present a new algorithm for recognition of jumps of unnatural origin in magnetograms. It is based on discrete mathematical analysis theory, which in turn relies on fuzzy logic principles. In particular, it involves such notions as fuzzy comparison and fuzzy bound, which allows introduction of "measure of jumpiness" functional. The latter is used directly to classify each value of original record as jump-related or not. The algorithm's free parameters ensure its flexibility and adaptivity, as they may be adjusted for processing different types of time series.
We demonstrate the algorithm performance by example of the three component magnetograms, recorded by GOES 15 satellite on 3 April 2010. Most of the detected jumps coincide with automatic switches of the heater systems paired with each magnetometer; the origin of the other ones is unknown. If needed, the detected jumps can be further removed from the records by operators or decision makers. Our plans include more systematic JM application to the new generation GOES 16 data (Loto'aniu et al., 2018, The GOES 16 Spacecraft Science Magnetometer, in-preparation for submission to Advances in Space Research) and its efficiency estimation as applied to data under different geomagnetic conditions, contaminated by geomagnetic pulsations, etc. For that reason, the algorithm will have to be adjusted by choosing proper set of free parameter values, as GOES 16 data have different sampling rate and some other features.
Agayan, S., S. Bogoutdinov, A. Soloviev, R. Sidorov (2016), The study of time series using the DMA methods and geophysical applications, Data Sci. J., 15, no. 16, p. 1–21, https://doi.org/10.5334/dsj-2016-016.
Agayan, S. M., Sh. R. Bogoutdinov, R. I. Krasnoperov (2018), Short introduction into DMA, Russ. J. Earth Sci., 18, p. ES2001, https://doi.org/10.2205/2018ES000618.
Balasis, G., et al. (2013), Magnetospheric ULF wave studies in the frame of Swarm mission: a time-frequency analysis tool for automated detection of pulsations inmagnetic and electric field observations, Earth, Planets and Space, 65, p. 1385–1398, https://doi.org/10.5047/eps.2013.10.003.
Gvishiani, A. D., S. M. Agayan, Sh. R. Bogoutdinov (2008a), Fuzzy recognition of anomalies in time series, Dokl. Earth Sci., 421, no. 1, p. 838–842, https://doi.org/10.1134/S1028334X08050292.
Gvishiani, A. D., S. M. Agayan, Sh. R. Bogoutdinov, J. Zlotnicki, J. Bonnin (2008b), Mathematical Methods of Geoinformatics: III. Fuzzy Comparisons and Recognition of Anomalies in Time Series, Cybernet Sys. Analys., 44, no. 3, p. 309–323, https://doi.org/10.1007/s10559-008-9009-9.
Gvishiani, A., et al. (2014), Survey of Geomagnetic Observations Made in the Northern Sector of Russia and New Methods for Analysing Them, Surveys in Geophysics, 35, no. 5, p. 1123–1154, https://doi.org/10.1007/s10712-014-9297-8.
Friis-Christensen, E., H. Lühr, G. Hulot (2006), Swarm: A constellation to study the Earth's magnetic field, Earth, Planets and Space, 58, p. 351–358, https://doi.org/10.1186/BF03351933.
Kulchinsky, R. G., E. P. Kharin, I. P. Shestopalov, A. D. Gvishiani, S. M. Agayan, Sh. R. Bogoutdinov (2010), Fuzzy logic methods for geomagnetic events detections and analysis, Russ. J. Earth Sci., 11, no. 4, p. RE4003, https://doi.org/10.2205/2009ES000371.
Love, J. J., A. Chulliat (2013), An international network of magnetic observatories, Eos Trans. Am. Geophys. Union, 94, no. 42, p. 373–374, https://doi.org/10.1002/2013EO420001.
Mandrikova, O. V., V. V. Bogdanov, I. S. Solov'ev (2013), Wavelet analysis of geomagnetic field data, Geomagn. Aeron., 53, no. 2, p. 268–273, https://doi.org/10.1134/S0016793213020102.
Ouadfeul, S. A., V. Tourtchine, L. Aliouane (2015), Daily geomagnetic field prediction of INTERMAGNET observatories data using the multilayer perceptron neural network, Arab. J. Geosci., 8, p. 1223, https://doi.org/10.1007/s12517-014-1308-z.
Reda, J., D. Fouassier, A. Isac, H.-J. Linthe, J. Matzka, C. W. Turbitt (2011), Improvements in geomagnetic observatory data quality, Geomagnetic Observations and Models, Vol. 5, p. 127–148, Springer Science + Business Media, B.V (IAGA Special Sopron Book Series).
Singer, H. J., L. Matheson, R. Grubb, A. Newman, S. D. Bouwer (1996), Monitoring space weather with the GOES magnetometers, GOES-8 and Beyond, Proc. SPIE, vol. 2812, edited by E. R. Washwell, p. 299–308, Int. Soc. for Opt. Eng., Bellingham, Wash.
Soloviev, A., et al. (2012a), Automated recognition of spikes in 1 Hz data recorded at the Easter Island magnetic observatory, Earth, Planets and Space, 64, no. 9, p. 743–752, https://doi.org/10.5047/eps.2012.03.004.
Soloviev, A. A., S. M. Agayan, A. D. Gvishiani, Sh. R. Bogoutdinov, A. Chulliat (2012b), Recognition of disturbances with specified morphology in time series: Part 2. Spikes on 1-s magnetograms, Izvestiya, Physics of the Solid Earth, 48, no. 5, p. 395–409, https://doi.org/10.1134/S106935131204009X.
Soloviev, A., Sh. Bogoutdinov, A. Gvishiani, R. Kulchinsky, J. Zlotnicki (2013), Mathematical Tools for Geomagnetic Data Monitoring and the INTERMAGNET Russian Segment, Data Sci. J., 12, p. WDS114–WDS119, https://doi.org/10.2481/dsj.WDS-019.
Soloviev, A., S. Agayan, S. Bogoutdinov (2016), Estimation of geomagnetic activity using measure of anomalousness, Ann. Geophys., 59, no. 6, p. G0653.
Zhang, S., et al. (2016), Quality Control of Observation Data by the Geomagnetic Network of China, Data Sci. J., 15, p. 15, https://doi.org/10.5334/dsj-2016-015.
Zlotnicki, J., J.-L. LeMouel, A. Gvishiani, S. Agayan, V. Mikhailov, Sh. Bogoutdinov (2005), Automatic fuzzy-logic recognition of anomalous activity on long geophysical records. Application to electric signals associated with the volcanic activity of la Fournaise volcano (Réunion Island), Earth Planet. Sci. Lett., 234, p. 261–278, https://doi.org/10.1016/j.epsl.2005.01.040.
Received 15 May 2018; accepted 2 July 2018; published 25 August 2018.


Citation: Soloviev A., Sh. Bogoutdinov, S. Agayan, R. Redmon, T. M. Loto'aniu, H. J. Singer (2018), Automated recognition of jumps in GOES satellite magnetic data, Russ. J. Earth Sci., 18, ES4003, doi:10.2205/2018ES000626.
Copyright 2018 by the Geophysical Center RAS.