RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 18, ES4001, doi:10.2205/2018ES000624, 2018
F. A. Mkrtchyan1, S. M. Shapovalov2
1Kotelnikov Institute of Radioengineering and Electronics of the Russian Academy of Sciences, Moscow, Russia
2Shirshov Institute of Oceanology of the Russian Academy of Sciences, Moscow, Russia
The problems of remote monitoring systems for detection and classification of anomalous phenomena in the environment with appropriate algorithms and software are considered. The technique of detecting and classifying anomalous phenomena in the investigated medium suggested in this paper allows us to solve the problems of measurement and detection on a real time basis. A scientific basis for multi-channel remote monitoring systems has been developed. New methods and algorithms for processing remote sensing data and formation of updated databases for improving our knowledge about environment were used. The system is based on modern computer technologies and high-performance computing systems. It is clear that the analysis of integrated contact and remote measurements can increase reliability of estimations of parameters of natural systems and solve the problem of planning of these measurements. Application of remote monitoring is related in many cases to the acceptance of the statistical decision about the existence of any given phenomenon on a surveyed part of the study site. One of the features of information gathering for such a decision is the impossibility of obtaining statistical samples in large amounts. Therefore, it is necessary to develop the optimum algorithms of identification of random signals characterized by the samples of limited data under the conditions of a priori parametric indefiniteness.
Development and organization of remote monitoring systems (RMS) is an exclusively difficult, complex, multidisciplinary problem. Experimental methods of environmental research play an important role in its solution. The primary issues of the realization of such experiments are mass gathering of the information on the studied object, efficiency of its processing, and authentic data interpretation on the basis of analytical and numerical mathematical models. Therefore, within the limits of RMS application it is possible to allocate the systems of the automated radio physical experiments aimed at the following functions [Armand et al., 1987, 1997; Mkrtchyan, 1982]:
Effective implementation of these functions under modern conditions implies wide automation of the radio-physical experiment, using the latest achievements of experimental techniques and methods of processing the observational data. Automation of radio-physical methods of environmental research opens new opportunities for the researcher, namely:
A huge amount of information requires involvement of complex technical and software tools that ensure efficient processing, storage, and retrieval of the necessary information about the objects. Successful implementation of the experiment often requires involvement of a large number of a priori information. Therefore, it is necessary to organize long-term storage of a large amount of data and provide reference data and information service on the data availability.
The complex and diverse structure of data from radio-physical experiments results from the following: technical complexity of data recording devices, variety of these devices, and multistage nature of research. Hence, coordination of the information between different stages of processing and analysis is needed, as well as the development of optimal methods for processing information containing conditions for the operational coordination of various types of computers and data recording devices.
A large number of users of radiometric information with a wide range of requirements implies, on the one hand, centralized storage of data about the state of the environment and the development of universal tools for processing these data. On the other hand, the variety of data and functional tasks of data processing requires the development of special software.
Based on the abovementioned features of radio-physical methods of environmental studies, we can formulate the following principles for designing automated systems for collecting and storing information in RMS:
A systematic approach to the automation of radio-physical experiments includes combination of the theoretical research methods with the technical and software tools integrated into an automated complex for obtaining and processing radiometric information [Armand et al., 1987, 1997; Mkrtchyan, 2010a].
One of the functions of RMS is the detection and classification of anomalous phenomena in the study site. It is important to consider the conditions of uncertainty in the location and possible dynamics of the anomaly in the study site.
 |
| Figure 1 |
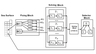
Limited efficiency, memory size, and operation speed of onboard computers requires separation of the monitoring system into three subsystems (Figure 1): Fixing Block (measuring block), Solving Block, and Selector Block. The subsystems consist of the blocks with the following functions: (1) periodic viewing of the sea surface elements; (2) recording "suspicious" elements in the memory; (3) formation of the anomaly motion from the traces of suspicious elements; (4) accumulation of the time series of the data about fixed "suspicious" elements of a terrestrial surface to make a statistically based decision whether these data are related to the noise or signal; (5) multistage localization of the anomaly search procedure.
Fixing Block includes the general scanner $\Phi1$ and memory $\Phi3$, and also $m$ blocks ($\Phi2i$) for primary criteria $k_{1i}$ for each channel $(i = 1, m)$. Scanning of the studied regions is performed using block $\Phi1$. As a result of the operation of blocks $\Phi2i$ coordinates of the "suspicious" elements of the region are transferred and recorded in the free cells of memory $\Phi3$.
Solving Block consists of $m$ $Pi$ blocks, each of which consists of $P_{1i}$ blocks, analyzer, and the block of secondary criterion $k_{2i} \; (i = 1, m)$. These blocks for each channel determine together the noise or anomalous nature of the signals among the "suspicious" elements found in the region.
Solving Block "$k$ of $m$". In this block a fixed "suspicious" element is classified. If at least $k$ channels from the total $m$ channels fix the anomalous nature of the "suspicious" element, then block ("solver $k$ of $m$") makes the final decision on the signal character of the fixed element. Otherwise, a decision is taken about the noise character of the element [Armand et al., 1997; Mkrtchyan, 2010a, 2015]. After making a decision about the noise character of the analyzed element, the corresponding memory cells of memory $\Phi3$ are erased and can record new data. If it is decided that the analyzed element is not noise, but a signal, then a command is given to Selector Block for more precise localization of the anomalous element, and the corresponding cells of the $\Phi3$ memory are also erased.
Selector Block consists of block $\Pi$ for optimum multistage search and $n$ devices ($I1$, $I2, \ldots, In$) whose functions are consecutive specifications of the location of anomalies in the specific element of the region according to the data of block $\Pi$.
It is important that the space is quantized by elements. This is determined by the resolution of the applied measuring equipment.
Due to the dynamic change of the anomalies in time, the monitoring system should monitor these changes. Therefore, it must perform periodic viewing of space elements much faster than this change occurs. The system should also have time to process the stream of the statistical information. The efficiency of the system is determined by the ability to control these parameters.
The RMS should use $n$ satellites of the similar type, moving at speed $V$, uniformly located on a cyclic orbit of length $L$. In this case, RMS returns to the same place in the region with interval $h$, which must satisfy the following relation
\begin{eqnarray*} h= \frac{L}{nV} < \Delta \nu \end{eqnarray*}where $\Delta$ is the primary linear resolution of RMS, $\nu$ is the velocity of the motion of anomalies. The quality of RMS is determined by probabilities $F$ of the false alarm and $D$ of the correct detection, the mean detection time of $ht$ anomalies including the pure time of search and the highly probable time of trouble-free functioning of the RMS. The quality of RMS is also provided by kinematic parameter $h$, energetic parameter $E$, the amount of memory, and the technical reliability parameter, which is the probability of failure-free operation of RMS during time $ht$. Parameter $E$ determines the signal-to-noise ratio when anomalies are detected.
The number of elements of resolution $N$ in the study region is
\begin{eqnarray*} N= \frac{S}{\Delta^2} \end{eqnarray*}To have high detection accuracy, it is necessary that $N > M$. As a result, the detection procedure breaks down into two stages [Armand et al., 1987, 1997; Mkrtchyan, 1982]. At the first stage of detection, the memory cells record the coordinates of the "suspicious" elements of the region. At the second stage, the final decision is made on the noise or signal character of the $n_i$ element of the region
\begin{eqnarray*} n_i = f_i (F,D,E), \quad i=0 \;\mathrm{or} \; 1 \end{eqnarray*}where function $f_i$ depends on the statistical detection procedure.
We assume that the memory size of the monitoring system is limited by $M$ cells, and the information stream is capable to process $N$ space elements. In each element, the source of the information is defined by stochastic function $\xi_i(t)$. If $M \geq N$, the solution of the problem of the statistical analysis of the information stream is reduced to the accumulation of data in the memory cells and its subsequent processing using the methods of mathematical statistics. In case when $M < N$ it is necessary to develop an algorithm of accumulation of statistics related only to the "suspicious" elements of the information stream. Depending on the signal-to-noise ratio stochastic function $\xi_i(t)$ is defined by probability density $f_a(x)$. Let the choice of "suspicious" elements in the memory of the monitoring system correspond to the case $\xi > X$, where $X$ is the specified threshold. If $a = a_0$ for the noise only in the stream $\xi_i(t)$ and $a = a_1$ for the signal plus noise, then the probabilities of fixing of signal and noise elements would be written as
\begin{eqnarray*} p_S= \int \limits_X^\infty f_{a_1} (x) dx, \quad p_N= \int \limits_X^\infty f_{a_0} (x) dx \end{eqnarray*}We assume that the proportions of the signal and noise elements at time moment $t$ are equally distributed in space as $1-\gamma(t)$ and $\gamma(t)$, respectively. Then, the random number $\kappa(t)$ of the "suspicious" elements fixed at time moment $t$, would have the following distribution:
\begin{eqnarray*} P[k(t)=k]= P_{N\gamma ,p_N} (k_1) \times P_{N[1-\gamma],p_S} (k_2 ) \end{eqnarray*} \begin{eqnarray*} P_{n,p} (m)= C_n^m p^m (1-p)^{n-m} \end{eqnarray*}Knowing the needed time interval for the realization of one survey of the study region related to a fixed time unit, we can calculate the probability of memory overflow of the monitoring system $P[\mu(t) > M$] at time moment $t$. We will consider the case of discrete time, when the moments of occurrence and the termination of processing of the elementary noise or signal are identified with the nearest integer. We assume that each specific element is processed in a separate cell of memory up to the moment of the final decision whether it has the noise or signal character. After that the memory cell is cleared, and it can receive further information. In this case the number $\mu(t)$ of the memory cells occupied at time moment $t$ is represented as an ordinary integer function.
Let us introduce the following functions
\begin{eqnarray*} g_t (x)= \sum\limits_{k=0}^\infty P[k(t)=k] x^k \end{eqnarray*} \begin{eqnarray*} G_t (x)= \sum\limits_{m=0}^\infty P[\mu(t)=m] x^m \end{eqnarray*}Let us consider that processing time of one element at the moment $t=s$ is a random variable $\nu(s)$ with the specified distribution $P[\nu(s) < t ] = F_s(t)$. Then we have:
\begin{eqnarray*} G_t (x) = \prod\limits_{s=h}^t g_s \{ 1+ [1-F_s (t-s)] (x-1)\} \end{eqnarray*}Further, we get the following expressions for the mean value and dispersion:
\begin{eqnarray*} E \mu(t)= \sum\limits_{s=h}^t Ek(s)[1-F_s (t-s)] \end{eqnarray*} \begin{eqnarray*} D_\mu(t)= E \mu(t) + \end{eqnarray*} \begin{eqnarray*} \sum\limits_{s=h}^t [Dk(s)-Ek(s)][1-F_s (t-s) ]^2 \end{eqnarray*}If $\kappa(s)$ is characterized by the Poisson distribution with parameter $\lambda(s) = E \kappa (s)=D \kappa(s)$, then $\mu(s)$ is also characterized by the Poisson law with parameter $\Lambda(t) = E\mu(t)$.
All these considerations are true if the value of $M$ is not limited. If $M =\mathrm{const} > \Lambda(t)$, then $\mu(s)$ is characterized by the truncated Poisson distribution
\begin{eqnarray*} P \,[\mu(t)=m; M=\mathrm{const}]= P_{\Lambda(t),M} (m)= \end{eqnarray*} \begin{eqnarray*} \Bigl(\frac{\Lambda^m (t)}{m!}\Bigr) \Bigl/\sum\limits_{l=0}^m \frac{\Lambda^l (t)}{l!}, \quad \quad m < M \end{eqnarray*}Consequently, the efficiency of the monitoring system is determined by the probability of the overflow of its memory, i.e. the probability of the information losses. In a more general case, to assess the efficiency of the monitoring system for detecting anomalies on the Earth's surface, it is necessary to consider the operation of all its subsystems, taking into account their individual memory limits and data processing speed.
The criteria for assessing the efficiency of the monitoring systems are ultimately determined by the probability of the performance of their tasks, which is a complex function of the parameters of the systems and the environment. In the case of the theoretical considerations, the model of the environment plays an important role. One of the possible models of this kind is based on the use of the concept of "patchiness" of the space under study. The mobile anomaly breaks the spotted structure; as a result its trace is formed. Since the patches can have different nature, the efficient detection algorithm must be multi-channel, capable of analyzing hydrophysical, biological, acoustic, optical, and physico-chemical information.
The probability of the overflow of the memory of the solution block during running time $T_{\Sigma}$ is estimated as:
\begin{eqnarray*} P \geq 1-T_\Sigma \{1- \Phi[(M- \Lambda) \Lambda^{-1/2} ]\} \end{eqnarray*}where $\Phi$ is the Gaussian integral.
The accuracy of this assessment depends on the algorithmic filling of the monitoring system blocks. In particular, when using the method of sequential analysis to solve the problem of distinguishing hypotheses and evolutionary forecasting technology, the data processing procedure in the solution block is greatly simplified and, consequently, the speed of decision making is increased, reducing the data delay between the lock and the solution block. Consideration of the theoretical estimates of the magnitude of such delays is an independent task.
All the following discussion will be focused on the details of the MS solver associated with the uncertainty of the probability distributions of the anomalies and the background that are typical for monitoring situations. This section deals with the case of the known distributions, and the specificity of monitoring is associated with the multi-channel detection of anomalies.
The MS subsystem Solving Block is based on the classical and sequential procedures for choosing between two hypotheses. These procedures require setting the probability densities $f_{\omega_0}(x)$ and $f_{\omega_1}(x)$, which are usually unknown. Usually empirical analogues (histograms) $f^*_{\omega_0}(x)$ and $f^*_{\omega_1}(x)$ obtained from the "training" samples of the limited volume $n_0$ and $n_1$, are usually known best of all. Therefore, the developed theory can be used only for sufficiently large values of $n_0$ and $n_1$, when the probability of converges with $f_{\omega}(x)$. In the general case of development, the theory can serve to obtain the best estimates of the procedures under consideration.
The problem of detecting anomalies on the Earth's surface has a specificity associated with the so-called patchiness of the studied space. Violation of the parameters of the patchiness can be a sign of the appearance of anomalies in the study region. In real conditions, the study of the patchiness of the medium and the acquisition of statistical data in the Solver is a complex and time-consuming task.
To solve the detection problems, statistical distributions of the patchiness of the background are necessary. Patchy land has been studied by geo-botanists for long [Mkrtchyan, 1982] using the method of the so-called transepts, which have a common statistical significance. We are only beginning to investigate the elements of the sea surface [Mkrtchyan, 2010a, 2010b; Mkrtchyan and Krapivin, 2010]. In the ocean, the line of the transept corresponds to the line of the vessel's route.
Practically the most acceptable method to determine patches is the method of setting thresholds. In this case, part of the space on which the index of the medium over the given channel exceeds ($l^+$-characteristic) or does not exceed the ($l^-$- characteristic) threshold value belongs to the patch region.
To detect the anomalies on the Earth's surface, the signals can be drawn from different channels: temperature, acoustic, biological, optical, etc. It will be shown below that the construction of a subsystem of multichannel detection will result in a greater efficiency than the investigation of each of these channels separately [Mkrtchyan, 1982, 2015].
To detect anomalies on the water surface of one of the training samples, one can take, for example, the background ($l^+, l^-$)-characteristics. Then, one can use phytoplankton signal during the occurrence of anomalies as a second training sample.
The study of background ($l^+, l^-$)-characteristics in almost all channels and the construction of histograms show that the amplitude characteristics have normal distributions, and the ($l^+, l^-$)-characteristics have exponential distributions. Therefore, consideration of the optimal decision procedures for these distributions is important.
As noted above, for large values of $n_0$ and $n_1$, the MS solver can be based on the classical and sequential selection procedures between hypotheses.
If the probabilistic characteristics $f_{\omega_0}(x)$ and $f_{\omega_1}(x)$ of the anomaly and the background are determined and have the form of the normal or exponential distribution, respectively,
\begin{eqnarray*} f_\omega (x)= \left\{ \begin{array}{l} \displaystyle\frac{1}{\sigma\sqrt{2 \pi}} \exp\Bigl[- \frac{(x-\omega)^2}{2\sigma^2}\Bigr] \omega \exp(-\omega k) \end{array} \right. \end{eqnarray*} |
| Table 1 |
then the average values $E_0\nu$, $E_1\nu$ (sample volumes needed to determine the noise or signal character of a given sample) can be calculated using the formulas given in Table 1. These formulas take into account the possibilities of using classical and sequential hypothesis selection procedures.
We used the following notations: $\alpha (\beta)$ is the probability of the error of the first (second) kind; $u_{\alpha}$ and $u_{\beta}$ are quantiles of the normal distribution; $A=(1-\alpha)/\beta$ and $B=\alpha/(1-\beta)$ are the thresholds of the sequential procedure.
Similar calculations can be carried out for any other form of the dependence of the probability densities $f_{\omega_0}(x)$ and $f_{\omega_1}(x)$. However, in the real situation it is better to use empirical distributions $f_{\omega_0}(x)$ and $f_{\omega_1}(x)$ instead of these dependencies. Therefore, in case of limited $n_0$ and $n_1$ in the Solver Block it is possible to use optimal learning algorithms for normally distributed random and exponentially distributed quantities, described in [Armand et al., 1987; Mkrtchyan, 1982]. In the case when little is known about the background and distributions of the anomalies, modern procedures for pattern recognition can be used. However, unlike optimal learning algorithms for normally and exponential distributed random values it is impossible to make similar calculations for procedures of pattern recognition so far, since the average values of errors of the first and second kind ($\bar{\alpha}=\bar{F}$ and $1-\bar{\beta}=\bar{D}$) for them are still unknown. Therefore, we shall further confine ourselves to an algorithmic description of these very efficient procedures used in the conditions of greater uncertainty than the above-mentioned optimal procedures.
Let us analyze in detail the effect that can be obtained from multichannel procedures.
Let $D_i$ be the probability of correct detection of the $i$th channel ($i = 1, m$), where $F_i$ is the probability of false alarm ($i = 1, m$). If we take a decision using the rule "$m$ of $m$", then the corresponding probabilities of correct detection $D$ and false alarm $F$ would be equal to
\begin{eqnarray*} F= \Pi_{i=1}^m F_i, \; \; D=\Pi_{i=1}^m D_i \end{eqnarray*}$ 1> D_i > 0.5 > F_i > 0$, respectively. It is clear that in this case $F$ improves, but $D$ becomes worse.
We now consider the rule "$k$ of $m$". For simplicity, we first assume that $F_1 = F_2 = \ldots = F_i = \ldots = F_m$, $D_1 = D_2 = \ldots = D_i = \ldots = D_m$. Then:
\begin{equation} \tag*{(1)} \begin{array}{l} D=P\Bigl( \mu \geq \displaystyle\frac{k}{H_1} \Bigr )= 1- \sum\limits_{i=0}^{k-1} C_m^i D_1^i (1-D_1 )^{m-i} F=P\Bigl( \mu \geq \displaystyle\frac{k}{H_0} \Bigr )= \sum\limits_{i=0}^{k-1} C_m^i F_1^i (1-F_1 )^{m-i} \end{array} \end{equation}Using the results of [Mkrtchyan, 1982], we can write the asymptotic estimates of these sums:
\begin{eqnarray*} D=1-\sum_{i=0}^{k-1} C_m^i D_1^i (1-D_1 )^{m-1} \,> \end{eqnarray*} \begin{eqnarray*} 1-\exp [-mk(\frac{k}{m},D_1 )], \;\;\; D_1> \frac{k}{m} \end{eqnarray*} \begin{equation} \tag*{(2)} F= \sum_{i=0}^{k-1} C_m^i F_1^i (1-F_1 )^{m-i} \,< \end{equation} \begin{eqnarray*} \exp [-mk(\frac{k}{m},F_1 )], \;\;\; F_1 < \frac{k}{m} \end{eqnarray*} \begin{eqnarray*} k(x,y)= x \ln \bigl(\frac{x}{y}\bigr)+ (1-x) \ln \bigl( \frac{1-x}{1-y}\bigr) \end{eqnarray*}Since the number of channels in practice is not very large (of the order of five), we do recommend using formulas (1), not asymptotic formula (2). We shall use the exact formulas (1) in our specific calculations.
We introduce notations $\eta_D= 1-(1-D)/(1-D_1)$, $\eta_F= 1-F/F_1$. As can be seen, these values determine the relative efficiencies of the multichannel approach compared to the single-channel case.
In conclusion, we note that Selector Block is an MS node that produces a refinement search (localizes the location of the anomalies). The theory for the Selector Block can be based on the theory of optimal search and game theory [Armand et al., 1987, 1997; Mkrtchyan, 1982, 2010a].
Remote measurements consist of information acquisition, when the data of measurements, acquired from the tracks of the flying system along the routes of survey, are directed to the input of the processing system. As a result, a two-dimensional image of the investigated object is recorded. Statistical model of patchiness for the investigated space is one of the models of this image.
In real conditions, the study of patches, acquisition of their statistical characteristics for the procedure of detection is quite a complex problem. It is necessary to develop a criteria to distinguish the patches from the other phenomena. For example, it is necessary to determine such a threshold, which serves as the patch indicator if the threshold is exceeded. It is also necessary to develop a model presentation of the processes of patch detection.
Threshold determination is the most obvious and simple method for patch definition. In this case, the part of space belongs to the region of patch, in which the parameter of environment measured within the chosen channel exceeds value ($l^+$) or, on the contrary, does not exceed the threshold value ($l^-$). Let $y = y (x_1, x_2$) be a function of coordinates ($x_1, x_2$) of points within considered region. If we delineate the "level surface" $y =$ const on the surface of the region, then closed curves of the $y$ level that bound the "patches" are projected onto it.
The algorithms for simulation of patchiness are based on the numerical solution of the algebraic inequalities determining coordinates of internal points of patches. It is impossible to write the equation of contours of patches in general. Therefore, contours of patches are described by a system of simple algebraic equations $\Sigma \varphi_i (x, y) =0$, where $\varphi_i (x, y)$ is the equation of an elementary curve. To simplify the software implementation of simulation of patchiness image, the equation of the circle with the varying coordinates of the center and radius is taken as the $\varphi_i (x, y)$. Complex forms of patches are formed by overlapping of several circles with different parameters on a plane of the drawing. This is defined by the following system of inequalities:
\begin{eqnarray*} \sum \{(x-a_i)^2 + (y-b_i)^2 - r_i\} \leq 0 \end{eqnarray*}where $x$, $y$ are the Cartesian coordinates of internal points of patches, $a_i$, $b_i$, $r_i$ are coordinates of the centre and radius of the $i$-th circle, respectively, and $n$ is a number of the circles composing the model image.
To simulate the randomness of the background distribution of patches the patchiness model parameters $a_i$, $b_i$, $r_i$ are set by means of random-number generators. By changing the laws of the distribution of random numbers and their statistical parameters, it is possible to obtain statistically different patchiness images.
The criteria of estimation of the efficiency of the monitoring systems are defined by the probability of their operation with the given tasks, which is a complex function of parameters of the systems and environment. According to the theoretical viewpoint the environmental model plays an important role. One of such possible models is being constructed using the concept of "patchiness" of the studied region. Mobile anomaly breaks the patchiness structure and as a result its trace is formed. Since the patches can have various natures, the efficient algorithm of the detection should be multichannel, capable to analyze the hydrophysical, biological, acoustic, optical, physical, and chemical information [Armand et al., 1987, 1997; Mkrtchyan, 1982, 2010a, 2010b].
 |
| Figure 2 |
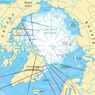
Figure 2 shows the example of the application of RMS for monitoring of brightness temperature of the surface of the Arctic Ocean based on the data of space satellite Cosmos 1500 (8–9 February 1984). The data were obtained from satellite Cosmos 1500, where radiometers have been installed at the wavelengths $\lambda_1 = 0.8$ cm, $\lambda_2 = 1.35$ cm, $\lambda_3 = 8.5$ cm.
The statistical data processing the microwave-radiometric measurements from satellite Cosmos 1500 allow to properly classify large-scale processes of the study of the Arctic ice cover. In particular, it is possible to determine the position of the edge of the ice. The ice cover is divided into 4 groups: ice-free water, one year ice, multi-year ice, and pack ice. The results of processing are shown in Figure 2. We get 4 clusters, which meet the following conditions on investigated surface: 1 – ice-free water; 2 – one-year ice; 3 – multi-year ice; 4 – pack ice. The errors of the detected boundaries of the above clusters are as follows: 1 – 26%; 2 – 30%; 3 – 17%; 4 – 12%.
As noted above, the criteria of effectiveness of the monitoring systems are ultimately determined by the fact whether the system completes the task or not. This probability is a complex function of the parameters of the systems themselves and of the marine environment. One of the possible models of this kind is based on the use of the concept of sea surface "patchiness".
The mobile anomaly destroys the patchy structure and, as a consequence, its trace is formed. Since the patches can have different nature, an effective detection algorithm must be multi-channel.
It follows from the aforesaid that statistical characteristics of "patchiness" of the brightness temperatures in the microwave range can be used for detection and classification of the phenomena on the ocean surface.
The analysis of empirical histograms for "patchiness" of the brightness temperatures in the microwave range shows that in most cases ($l^+, l^-$)-characteristics would be consistent with the exponential distribution, and amplitude characteristics would correspond to the normal distribution. Therefore, to detect and classify the phenomena on the ocean surface it is necessary to apply optimal algorithms for the computer training. This will allow to make statistical decisions about the aforesaid distributions.
Armand, N. A., V. F. Krapivin, F. A. Mkrtchyan (1987), Methods of Data Processing of Radiophysical Research of an Environment, 270 pp., Nauka, Moscow (in Russian).
Armand, N. A., V. F. Krapivin, F. A. Mkrtchyan (1997), GIMS-technology as new approach to the information support of the environment study, Problems of the Environment and Natural Resources, no. 3, p. 31–50 (in Russian).
Mkrtchyan, F. A. (1982), Optimal Distinction of Signals and Monitoring Problems, 185 pp., Nauka, Moscow (in Russian).
Mkrtchyan, F. A. (2010a), Problems of Statistical Decisions in Ocean Monitoring, Proceedings of the International Symposium of the Photogrammetry, Remote Sensing and Spatial Information Science, Volume XXXVIII, Part 8, Kyoto, Japan, 9–12 August, 2010, p. 1038–1042, ISPRS, Kyoto, Japan.
Mkrtchyan, F. A. (2010b), Statistical decisions for samples small volume, Proceedings PIERS in Cambridge, USA, July 5–8, 2010, p. 361–365, PIERS, Cambridge, USA.
Mkrtchyan, F. A. (2015), Problems of Statistical Decisions for Remote Monitoring of the Environment, Proceedings PIERS in Prague, July 6–9, 2015, p. 639–643, PIERS, Prague.
Mkrtchyan, F. A., V. F. Krapivin (2010), GIMS-Technology in Monitoring Marine Ecosystems, Proceedings of the International Symposium of the Photogrammetry, Remote Sensing and Spatial Information Science, Volume XXXVIII, Part 8, Kyoto, Japan, 9–12 August, 2010, p. 427–430, ISPRS, Kyoto, Japan.
Received 6 April 2018; accepted 17 May 2018; published 12 July 2018.


Citation: Mkrtchyan F. A., S. M. Shapovalov (2018), Some aspects of remote monitoring systems of marine ecosystems, Russ. J. Earth Sci., 18, ES4001, doi:10.2205/2018ES000624.
Copyright 2018 by the Geophysical Center RAS.