
RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 16, ES4004, doi:10.2205/2016ES000576, 2016
Mohammad Tabaeh Hayavi, Mohammad Abdideh
Department of Petroleum Engineering, Omidiyeh Branch, Islamic Azad University, Omidiyeh, Iran
Accurate estimation of in situ stresses of a subsurface formation is important to get a basic knowledge of formation structure and position of anomalies, groundwater flows, performing fracturing operations, drilling operations, oil and/or gas production stimulation, wellbore stability analysis, and coupled geomechanics-reservoir simulation in petroleum engineering. In this paper, at first a new method for estimation of minimum and maximum horizontal stresses in tectonically active area based on the modification of linear poroelastic model and minifrac test results is presented. The rock mechanical properties used in poroelastic model are determinded using the artificial neural networks. Then, this method is applied to field data in order to verify the applicability of the modified linear poroelastic model. The results indicated that the agreement between the results of minifrac test and modified linear poroelastic model is satisfactory. Furthermore, application of artificial neural networks in this methodology increases the accuracy of linear poroelastic model for estimation of horizontal stresses.
It is important to have a full knowledge of in-situ stresses before carrying out any rock stress analysis. The main reasons for the determination of horizontal in-situ stresses are:
Warpinski and Smith [1989] reported that in-situ stresses are clearly the most important factor controlling hydraulic fracturing. Hubbert and Willis [1957] confirmed this with simple sand-box laboratory tests and pointed out that the orientation of a hydraulic fracture is controlled by the orientation of the least principal stress and the pressure needed to propagate a hydraulic fracture is controlled by the magnitude of the least principal stress.
There are several proposed methods for estimation of continuous horizontal stress profile including uniaxial strain model, tectonic stress boundary, tectonic strain boundary, and plain strain model. Hareland and Harikrishnan [1996] proposed a new method of minimum horizontal stress profiling based on drilling data. This method utilizes a normalized form of the Mohr failure envelope equation fit different lithologies.
Using the elasticity theory for isotropic rock and above principal stress assumption, it was possible to predict the magnitude of the horizontal stress. Blanton and Olson [1999] developed new constants which involved the properties of the rock, Young's modulus and Poisson's ratio for each incremental measurement. This method incorporates the tectonic, thermal effect and rock mechanical properties at each incremental depth. Both conventional and the Blanton Olson method assume horizontal strain in one direction equal to zero.
Minimum horizontal stress in unconventional formation is often calculated by the transverse isotropic vertical method. A calibrated anisotropic stress model provides a stress profile which better defines zone containment and often changes the perforating and staging strategy from that suggested by an isotropic model [Higgins, et al., 2008; Song, 2012]. This method assumes different rock properties and tectonic strain in different directions.
The minimum horizontal stress can be determined by direct measurement such as minihydraulic fracturing [e.g. Haimson and Cornet, 2003], leak-off test (LOT) and extended leak-off test (XLOT) [e.g. Raaen et al., 2006, Zhang and Roegiers, 2010].
The leak-off pressure is often taken as an upper bound of minimum horizontal stress. The most reliable estimate of minimum horizontal stress is obtained by injection tests including minifrac (pump in/flow back, pump in/shut in) tests [Teichrob et al., 2010].
The Minifrac test is performed before the main hydraulic fracturing treatment to obtain critical job design and execution data, and to confirm the predicted response of the treatment interval [Aadnoy and Looyeh, 2011].
The maximum horizontal stress is the most difficult component of the stress tensor. It can be estimated where breakouts or drilling induced fractures are observed on image logs and where compressive strength or tensile strength is known [Teichrob et al., 2010].
Zoback et al. [1987] proposed a methodology for determination of maximum horizontal stress when the rock strength is known utilizing observations of breakout width. Zoback [2007] concluded that drilling-induced tensile fractures occur in vertical wells whenever there is a significant difference between the two horizontal stresses. So, it can easily be shown that the condition for tensile fracture formation in the wellbore wall in a vertical well leads to estimation of maximum horizontal stress. Brudy et al. [1997] pointed out that the value of maximum horizontal stress required to induce drilling-induced tensile fractures (after correcting for excess mud weight and cooling) must be considered as a lower-bound estimate. This is because the drilling-induced tensile fractures might have occurred even if there had been no excess mud weight or cooling of the wellbore wall. This represents an upper bound value of maximum horizontal stress.
The maximum horizontal stress can be estimated from a XLOT via the fracture reopening test [Zhang and Roegiers, 2010]. Following the work of Hubbert and Willis [1957], Haimson and Fairhurst [1970] proposed openhole hydraulic fracturing in vertical wellbores as a technique for determination of the orientation and magnitude of maximum horizontal stress. Hickman and Zoback [1983] reported that the hydraulic fracturing is not a viable method for determination of maximum horizontal stress in relatively deep and/or hot wells. The most important reason that hydraulic fracturing cannot be used to determine maximum horizontal stress in oil and gas (or geothermal) wells is that it is essentially impossible to detect fracture initiation at the wellbore wall during pressurization. In point of fact, depending on the stress state, the breakdown pressure may not be the fracture initiation pressure.
This paper will firstly present a method for estimation of in-situ horizontal stresses using the minifrac test data and linear poroelastic model. This is followed by application of this method in field case study. Finally, the impacts of geomechnical parameters on horizontal stresses are investigated.
The Methodology for determination of maximum and minimum horizontal stresses includes following steps.
 |
| Figure 1 |
The minimum horizontal stress magnitude in petroleum basins is commonly determined using hydraulic fracture-type test. This test, referred to as minifrac in the petroleum industry, is pumping test usually conducted in the design and execution of large scale fracture stimulation jobs [Reynolds at al., 2006]. A minifrac test creates a fracture perpendicular to the minimum principal stress (the minimum horizontal stress in either a strike-slip or normal stress regime) by increasing the pressure in an isolated section of the wellbore. After the fracture is created the pumps are stopped and the test interval is shut-in. The pressure in the wellbore initially declines rapidly, eventually slowing down and coming to an equilibrium pressure above hydrostatic (Figure 1). During this pressure decline the newly created fracture closes. The closure pressure corresponds to the instant when the walls of the fracture initially touch and hence equals the magnitude of the minimum principal stress [Gronseth and Kry, 1983].
Vertical stress magnitudes and plays a very important role in geomechanical analysis, and it is the most basic parameter input in analysis of hydraulic fracturing, sand production and wellbore stability analysis. Vertical stress is induced by the weight of the overlying formations. The vertical stress can be calculated by integration of rock densities from the surface to the depth of interest based on (1). In fact, density log can be used to calculate overburden stress [Perchikolae et al., 2010].
\begin{equation} \tag*{(1)} \sigma_v = g \int\limits_0^Z \rho (z) dh \approx \bar{\rho} gz \end{equation}where $\sigma_v$ is vertical stress (MPa), $z$ is depth of interest (m), $\rho(z)$ is the density as a function of depth (gr/cm$^3$), $g$ is gravitational acceleration (m/s$^2$) and $\bar{\rho}$ is the mean overburden density of rocks (gr/cm$^3$).
Pore pressure is an important parameter in any rock mechanics study of porous rock systems. The pore fluid will carry part of the total stresses applied to the system, while the solid framework will carry another part of total stress, i.e. effective stress [Perchikolae et al., 2010].
Availability of the 3-D velocity data from 3-D seismic surveys, reservoir pressure, drilling events, mud logs, electric logs and mud weights used in the offset wells can provide information for the pore pressure evaluations. One of the methods used for pore pressure estimation after drilling the well is based on using well-log data. In this method, the porosity dependent parameters, which can be interval transit time, bulk density, or conductivity, is plotted versus depth. The porosity dependent parameter should have an easily detectable trend since the porosity decreases with formation compaction. A deviation from normal pressure trend causes a transition into abnormal or subnormal pressure zone [Bourgoyne et al., 1991].
To obtain rock mechanical properties precisely, there is one way is to perform laboratory tests on the specimens obtained from core samples. However, extensive coring is not carried out in every depth routinely and it is expensive and time-consuming as well. In addition, measurements made on core material can be biased due to relaxation and alteration of cores after recovery [Keshavarzi and Jalili, 2014].
Thus, for calculating rock mechanical properties, the common approach is to use geophysical logs data as inputs to the elastic constants equations. Elastic constants vary with the porosity, fluid type in the porosity and the mineral composition of the rock; hence, both porous and non-porous rocks are considered in the equations below [Crain, 2010]. This means that these equations somehow average the rock mechanical properties over an interval of a rock mass. This approach allows for calculating a continuous presentation of rock mechanical properties with depth. The elastic moduli relationships, in terms of shear and compressional wave velocities and bulk density can be calculated from following equations [Alipour Tabrizy et al., 2012; Nauroy, 2011].
\begin{eqnarray*} v_d= \frac{V_p^2-2V_s^2}{2(V_p^2-V_s^2)} \end{eqnarray*} \begin{eqnarray*} E_d=\frac{\rho_b V_s [3V_p^2-4V_s^2]}{V_p^2-V_s^2} \end{eqnarray*} \begin{eqnarray*} \alpha =1- \frac{K_B}{K_R} \end{eqnarray*} \begin{eqnarray*} K_B =\rho_b \left( V_p^2 - \frac{4}{3} V_s^2 \right) \end{eqnarray*} \begin{eqnarray*} K_R=\rho_{gr} \left(V_p^2-\frac{4}{3} V_s^2 \right) \end{eqnarray*}where $v_d$ is the dynamic Poisson's ratio, $E_d$ is the dynamic Young modulus (GPa), $\alpha$ is Biot's coefficient, $V_s$ is shear wave velocity (km/s), $V_p$ is compressional wave velocity (km/s), $K_B$ is dynamic bulk modulus (GPa), $K_R$ is the rock modulus (GPa), $\rho_b$ is the bulk density (gr/cm$^3$) and $\rho_{gr}$ is the grain density (gr/cm$^3$).
But one should keep in mind that, using from shear and compressional wave velocities derived from geophysical logs and above equations directly, introduce lots of errors in determination of horizontal stresses. In order to diminish the effects of these errors and overcome to these overpredictions, in this study artificial neural networks (ANN) will be introduced for better result. A ANN is a synthetic computational system that tries to mimic neurons in the human brain to discover sophisticated relationships between parameters. The capability of ANNs in prediction of the complicated behavior of complex functions led us to utilize this system for prediction of the elastic moduli profiles [Nabaei et al., 2009].
A neural network is a parallel distributed processing system composed of two components: the node (also called processing element, artificial neuron or unit) and the connection [Khazaei and Shahbazi, 2005]. A parameter $W_{ij}$ (weight) is associated with each connection between two cells. Thus each cell in the upper layer receives weighted inputs from each node in the layer below and then processes these collective inputs before the unit sends a signal to other layers [Li and Bridgwater, 2000]. The application processes of an ANN model design include the following steps [Trippi and Turban, 1996]:
In this study, a generalized regression neural network and a multilayer feed forward network were used to predict rock mechanical properties.
Dynamic data can not directly be utilized to develop mechanical models. So, they should be first converted into static data through some calculation changes made and then used in geomechanical model [Abdideh and Fathabadi, 2013].
The minimum horizontal stress is obtained by solving the linear poroelasticity equation for horizontal stress with vertical stress set equal to overburden [Song, 2012].
\begin{eqnarray*} \sigma_h = \frac{v_s}{1-v_s} (\sigma_v - \alpha P_p )+ \alpha P_p \end{eqnarray*}Due to the discrepancy from measured values of horizontal stress magnitude in tectonically active area, it was considered necessary to add the tectonic stress by shifting the log-derived stress profile. By considering horizontal strain and deformation effect, Hooke's law can be applied to derive the horizontal stresses and strains relationships [Perchikolaee et al., 2010]. The following equations are obtained, and are used to calculate the minimum and maximum horizontal stresses with tectonic strain effects [Al-Qahtani et al., 2001].
\begin{equation} \tag*{(2)} \sigma_h = \frac{v_s}{1-v_s} (\sigma_v - \alpha P_p )+ \alpha P_p + \frac{v_s E_s}{1-v_s^2}\varepsilon_x + \frac{E_s}{1-v_s^2} \varepsilon_y \end{equation} \begin{eqnarray*} \sigma_H = \frac{v_s}{1-v_s} (\sigma_v - \alpha P_p )+ \alpha P_p + \frac{v_s E_s}{1-v_s^2}\varepsilon_y + \frac{E_s}{1-v_s^2} \varepsilon_x \end{eqnarray*}where $\sigma_h$ and $\sigma_H$ are the minimum and maximum horizontal stresses, respectively, $\varepsilon_x$ and $\varepsilon_y$ are are tectonic strains in maximum and minimum horizontal stresses directions, respectively. By rearranging (2), yield
\begin{eqnarray*} \varepsilon_{yi} + v_{si} \varepsilon_{xi} = \end{eqnarray*} \begin{equation} \tag*{(3)} \frac{1-v_{si}^2}{E_{si}} \left[ \sigma_{hi} - \frac{v_{si}}{1-v_{si}} (\sigma_{vi} - \alpha_i P_{pi})- \alpha_i P_{pi} \right] \end{equation}The added subscript $i$ in the (3) indicates that this term is associated with the particular depth at which the minimum horizontal stress has been measured with minifrac testing. By solving (3) for first two depths related to minifrac testing (depths $i$ and $i+1$) simultaneously, the magnitudes of $\varepsilon_x$ and $\varepsilon_y$ are determined and termed $\varepsilon_{xi}$ and $\varepsilon_{yi}$. Consequently, after calculation of tectonic strains in any two consecutive depths, the maximum and minimum horizontal strains calculated as follows:
\begin{eqnarray*} \bar{\varepsilon}_x = \frac{\Sigma_{i=1}^n \varepsilon_{xi}}{n} \end{eqnarray*} \begin{eqnarray*} \bar{\varepsilon}_y = \frac{\Sigma_{i=1}^n \varepsilon_{yi}}{n} \end{eqnarray*}Consequently, the minimum and maximum horizontal stresses calculated by the following equations
\begin{equation} \tag*{(4)} \sigma_h = \frac{v_s}{1-v_s} (\sigma_v - \alpha P_p )+ \alpha P_p + \frac{v_s E_s}{1-v_s^2}\bar{\varepsilon}_x + \frac{E_s}{1-v_s^2} \bar{\varepsilon}_y \end{equation} \begin{equation} \tag*{(5)} \sigma_H = \frac{v_s}{1-v_s} (\sigma_v - \alpha P_p )+ \alpha P_p + \frac{v_s E_s}{1-v_s^2}\bar{\varepsilon}_y + \frac{E_s}{1-v_s^2} \bar{\varepsilon}_x \end{equation} |
| Figure 2 |
The presented methodology will be applied to the Bangestan reservoir in one of oilfields located in the south west of Iran. This oil field is one of the most important Iranian super Giant oil fields, was discovered in 1956 and now has more than 450 producing wells. This oil field has an anticline structure 72 km long and 6 km wide with NW-SE trending symmetrical anticlinal, located in central part of north Dezful region. Its main reservoir is the Asmari formation and Bangestan group [Motiei, 1995]. Bangestan Group includes the thick Sarvak limestone (300 m to 1000 m thick) of Cenomanian-Turonian age and the thinner Illam formation (50 m to 200 m thick) of Santonian age (Figure 2). These two reservoirs form a single reservoir in most of the Dezful Embayment and capped by the thick Gurpi/Pabdeh marls [Rabbani and Bagheri Tirtashi, 2010].
 |
| Figure 3 |
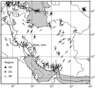
In absence of convincing stress-induced borehole failure (deriver from image log or four-arm caliper data), the azimuth of maximum horizontal stress can be derived from World Stress Map (WSM) data. According to worls stress map in Figure 3, this area has tectonically actived in millions of years ago which causes generation of numerous faulted zones. World stress map database showed the average azimuth of N20E [Moazzeni et al., 2011].
 |
| Figure 4 |
As mentioned before, in this study artificial neural networks is used for better results. The neural network, which was used in first step, is a feed forward back propagation with three layers and it is made of four neurons in input layer, twelve neurons in hidden layer and one neuron in output layer. Appropriate correlation coefficient was derived in validation process ($R = 0.91$) as shown in Figure 4. Compressional wave velocity, gamma ray, porosity and density for input and shear wave velocity were used as output, till our network is trained. Then, it can be used every well data as input for estimating shear wave velocity [Sabzehparvar and Nabi-Bidhendi, 2008].
 |
| Figure 5 |
In the second step, geomechanical parameters including Poisson's ratio, bulk modulus and Young's modulus were estimated from petrophysical logs comprising of GR, NPHI, RHOZ, DTCO, PEFZ ANN system. For this purpose, from two wells from the studied field full set logs along side with DSI data were used to calculating shear wave velocity. Figure 5 shows the results using this procedure. Accordingly, having input petrophysical data and target geomechanical parameters, a ANN model was trained and non-linear relationships between them were extracted [Mohammadi et al., 2012].
This procedure estimates any arbitrary function between input and output vectors, drawing the function estimate directly from the training data. Furthermore, it is consistent, in that as the size of the training set becomes large, the estimation error approaches zero, with only mild restrictions on the function. The magnitude of the range of data sets is significantly different for each input as well as across the inputs. This network training can be made more efficient by certain pre-processing steps [Dehghan et al., 2010].
Static values of Poisson's ratio and Young's modulus are both calculated via the following relations in south west of Iran. The results show good conformity with laboratorial data [Wang, 2000].
\begin{eqnarray*} v_s=v_d \end{eqnarray*} \begin{eqnarray*} E_s = 0.4145 E_d - 1.0593 \end{eqnarray*} |
| Figure 6 |
Rocks of Bangestan group have an average density of 2.6 gr/cm$^3$. Figure 6a shows the vertical stress and pore pressure profiles in the study area.
 |
| Table 1 |
Table 1 shows the magnitudes of $\varepsilon_{xi}$, $\varepsilon_{yi}$, and average tectonic strains in the Bangestan group. It can be seen that the average tectonic strains in maximum and minimum horizontal stresses directions calculated as 0.509 and 0.147, respectively .
In this study, results of minifrac test were used instead of leak-off test data. This fact is due to the leak-off pressures do not yield as reliable an estimate of the minimum horizontal stress magnitude as those determined from minifrac tests. This is largely because the disturbed stress field at the wellbore wall controls the leak-off pressure, and because the leak-off pressure must overcome any tensile strength of the formation [Reynolds et al., 2006]). For this study, closure pressures from minifrac tests were provided as shown in Figure 6b. Also, the maximum and minimum horizontal stresses profiles (using the equations (4) and (5)) are shown in Figure 6b. It can be concluded that the agreement between the results of minifrac test and modified linear poroelastic model is satisfactory.
This study presented a methodology for estimation of in-situ horizontal stresses using the minifrac test data and linear poroelastic model. Furthermore, the required geomechnical parameters are investigated using the artificial neural networks. The results indicated that the results of modified linear poroelastic model agreed well with the minifrac test data. Furthermore, neural network is a reliable approach for prediction of geomechanical parameters (applied to horizontal stress prediction model) from petrophysical logs and lead to accurate results from linear poroelastic model.
Aadnoy, B., R. Loooyeh (2011), Petroleum Rock Mechanics: Drilling Operation and Well design, First edition, Elsevier, New York.
Abdideh, M., M. R. Fathabadi (2013), Analysis of stress field and determination of safe mud window, Journal of Petroleum Exploration and Production Technology, 3, p. 105–110.
Alipour Tabrizy, V., Y. Mirzaahmadian (2012), Investigation of Sand Production Onset: A New Approach Based on Petrophysical Logs. SPE 150529, Proceedings of the SPE Annual Technical Conference and Exhibition. 15–17 February, Louisiana, p. 334–340, SPE, Louisiana, doi:10.2118/150529-ms.
Al-Qahtani, M., Z. Rahim (2001), A Mathematical Algorithm for Modeling Geomechanical Rock Properties of the Khuff and Pre-Khuff Reservoirs in Ghawar Field. SPE 68194, Proceedings of the SPE Annual Technical Conference and Exhibition 17–20 March, Bahrain, p. 123–129, SPE, Bahrain, doi:10.2118/68194-ms.
Blanton, T., J. Olson (1999), Stress Magnitudes from Logs: Effects of Tectonic Strains and Temperature, SPE Reservoir Evalution and Engineering, 5, p. 62–68, doi:10.2118/54653-PA.
Bourgoyne, A. T., M. E. Chenevert, K. Millheim, F. Young (1991), Applied Drilling Engineering. Textbook Series, 212–223 pp., SPE, Richardson, Texas.
Brudy, M., et al. (1997), Estimation of the complete stress tensor to 8 km depth in the KTB scientific drill holes: Implications for crustal strength, J. Geophys. Res., 102, no. 18, p. 1453–1475.
Crain, E. (2010), Crain's Petrophysical Handbook, Mindware, Alberta.
Dehghan, S., Gh. Sattari, S. Chehreh Chelgany, M. A. Aliabadi (2010), Prediction of uniaxial compressive strength and modulus of elasticity for Travertine samples using regression and artificial neural networks, Mining Science and Technology, 20, p. 41–46.
Gronseth, J. M., P. R. Kry (1983), Instantaneous shut-in pressure and its relationship to the minimum in-situ stress, Proc. Hydraulic Fracturing Stress Measurements, Monterey, p. 55–60, National Academy Press, Washington, DC.
Haimson, B., C. Fairhurst (1970), In situ stress determination at great depth by means of hydraulic fracturing, 11th Symposium on Rock Mechanics, p. 559–584, Society of Mining Engineers of AIME, W. Somerton.
Haimson, B. C., F. H. Cornet (2003), ISRM suggested methods for rock stress estimation, part 3: Hydraulic fracturing (HF) and/or hydraulic testing of pre-existing fractures (HTPF), International Journal of Rock Mechanics and Mining Science, 40, p. 1011–1020.
Hareland, G., R. Harikrishnan (1996), Comparison and Verification of Electric-Log-Derived Rock Stresses and Rock Stresses Determined From the Mohr Failure Envelope, Journal SPE Formation Evaluation, 6, no. 2, p. 219–222, doi:10.2118/26948-PA.
Hassanzadeh, G., M. Kobraei, A. Ahanjan, R. Tirtashi, M. Rashidi, M. Khaleghi (2011), Petroleum System Analysis Using Geochemical Studies, Isotope and 1D Basin Modeling in Hendijan Oil Field, SW Iran IPTC 14797, Proceedings of the International Petroleum Technology Conference, Bangkok, Thailand, 7–9 February, p. 85–92, PTC, Bangkok, Thailand, doi:10.2523/IPTC-14797-MS.
Heidbach, O., M. Tingay, A. Barth, J. Reinecker, D. Kurfe\ss, B. Müller (2009), The World Stress Map based on the database release 2008, equatorial scale 1:46,000,000, Commission for the Geological Map of the World, Paris, doi:10.1594/GFZ.WSM.Map2009.
Hickman, S. H., M. D. Zoback (1983), The interpretation of hydraulic fracturing pressuretime data for in situ stress determination, Hydraulic Fracturing Measurements, p. 55–62, National Academy Press, Washington, DC.
Higgins, S., S. Goodwin, A. Donald, T. Bratton, G. Tracy (2008), Anisotropic Stress Models Improve Completion Design in Baxter Shale, Proceedings of the SPE Annual Technical Conference and Exhibition, p. 1–10, SPE, Denver, Colorado, doi:10.2118/115736-ms.
Hubbert, M. K., D. G. Willis (1957), Mechanics of hydraulic fracturing, Pet. Trans. AIME, 210, p. 153–163.
Keshavarzi, R., S. Jalili (2014), Building a mechanical earth model and its application in a geomechanical analysis of hydraulic fracture behaviour in naturally fractured reservoirs, European Journal of Environmental and Civil Engineering, 18, no. 3, p. 336–357, doi:10.1080/19648189.2013.856035.
Khazaei, J., F. Shahbazi (2005), Modelling physical and physiological damage to wheat seeds under impact loading using artificial neural networks, Proc. International Conference on Agrophysics, Lublin, February 17–19, 2005, p. 11–24, PTC, Bangkok.
Li, Y., J. Bridgwater (2000), Prediction of extrusion pressure using an artificial neural network, Powder Technology, 2000, no. 108, p. 65, doi:10.1016/S0032-5910(99)00254-5.
Moazzeni, A., M. Nabaei, Kh. Shahbazi, A. Shadravan (2011), Mechanical Earth Modeling Improves Drilling Efficiency and Reduces Non-Productive Time (NPT), SPE 131718, Prepared for presentation at the SPE Deep Gas Conference and Exhibition held in Manama, Bahrain, 2521 January, p. 99–115, SPE, Bahrain.
Mohammadi, M., M. Kamali, A. Kadkhodaie, E. Kazemzadeh (2012), Estimation of geomechanical parameters from petrophysical data using Neuro-fuzzy systems, 15th Geophysical Conference, Iran, 5–8 Jul. 2012, p. 212–220, GCI, Iran.
Motiei, H. (1995), Petroleum Geology of Zagros-1, 589–600 pp., Geological Survey of Iran, Iran.
Nabaei, M., K. Shahbazi, A. Shadravan, M. Moazzeni (2009), Artificial neural network modelling enhances shear wave transit time. SPE 12158, Proceedings of the SPE Annual Technical Conference and Exhibition, 16–20 November, Kish Island, p. 170–182, SPE, Kish Island.
Nauroy, J. (2011), Geomechanics Applied to the Petroleum Industry, IFP Energies Nouvelles, p. 135–137, Elsevier, Paris.
Perchikolaee, S. R., et al. (2010), Building a Precise Mechanical Earth Model and its Application in Drilling Operation Optimization: A Case Study of Asmari Formation in Mansuri Oil Field. SPE 132204, Proceedings of the SPE Annual Technical Conference and Exhibition, 8–10 June 2010, p. 448–450, SPE, Bahrain.
Raaen, A. M., P. Horsrud, H. Kjolt, D. and (2006), Improved routine estimation of the minimum horizontal stress component from extended leak-off tests, International Journal of Rock Mechanics and Mining Science, 43, p. 37–48, doi:10.1016/j.ijrmms.2005.04.005.
Rabbani, A. R., A. Bagheri, R. Tirtashi (2010), Hydrocarbon Source Rock Evaluation of the Super Giant Ahwaz Oil Field, SW Iran Australian, Journal of Basic and Applied Sciences, 4, no. 5, p. 673–686.
Reynolds, D., S. Mildren, R. Hillis, J. Meyer (2006), Constraining stress magnitudes using petroleum exploration data in the Cooper–Eromanga Basins, Australia, J. Tectonophysics, 415, p. 123–140, doi:10.1016/j.tecto.2005.12.005.
Sabzehparvar, M., M. Nabi-Bidhendi (2008), Estimation of Elastic Parameters in Oil Reservoir with Using Well log Information and Neural network, Journal of Earth, 1, p. 23–33.
Song, L. (2012), Measurement of minimum horizontal stress from logging and drilling data in unconventional oil and gas, Msc thesis, University of Calgary, Calgary.
Teichrob, R., A. Kustamsi, G. Hareland, U. Odiegwu (2010), Estimating In Situ Stress Magnitudes and Orientations in an Albertan Field in Western Canada, ARMA 10-224, Proceedings of the 44th US Rock Mechanics Symposium and 5th U.S.-Canada Rock Mechanics Symposium, Salt Lake City, UT June 27–30 2010, p. 210–218, CRMS, Thailand.
Trippi, R. R., E. Turban (1996), Neural Networks in Finance and Investing-Using Artificial Intelligence to Improve Real-World Performance, McGraw-Hill, New York.
Wang, H. F. (2000), Theory of Linear Poroelasticity, Princeton University Press, Princeton.
Warpinski, N. R., M. B. Smith (1989), Rock mechanics and fracture geometry in recent advances in hydraulic fracturing, Journal of Society of Petroleum Engineers, Gidley, J. L. (Ed.) Recent Advances in Hydraulic Fracturing, 12, p. 66–73.
Zhang, J., J. Roegiers (2010), Discussion on Integrating borehole-breakout dimensions, strength criteria, and leak-off test results, to constrain the state of stress across the Chelungpu Fault, Taiwan, J. Tectonophysics, 492, p. 295–298.
Zoback, M., et al. (1987), In situ stress measurements in deep boreholes using hydraulic fracturing, wellbore breakouts and Stonely wave polarization, Rock Stress and Rock Stress Measurements conference, Jul. 22–25, 1987, p. 33–41, ISRM, Stockholm, Sweden.
Zoback, M. (2007), Reservoir Geomechanics, Cambridge University Press, Cambridge, doi:10.1017/CBO9780511586477.
Received 5 August 2016; accepted 8 September 2016; published 2 October 2016.


Citation: Hayavi Mohammad Tabaeh, Mohammad Abdideh (2016), Estimation of in-situ horizontal stresses using the linear poroelastic model and minifrac test results in tectonically active area, Russ. J. Earth Sci., 16, ES4004, doi:10.2205/2016ES000576.
Copyright 2016 by the Geophysical Center RAS.