
RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 20, ES4008, doi:10.2205/2020ES000737, 2020
A. Kurkin1, O. Kurkina1, A. Rybin1, T. Talipova2
1Nizhny Novgorod State Technical University n.a. R. E. Alekseev, Nizhny Novgorod, Russia
2Institute of Applied Physics RAS, Nizhny Novgorod, Russia
[1] Variability of the first baroclinic Rossby radius of deformation, $L_{R}$, in the Baltic, Black, Okhotsk, and Mediterranean seas is investigated. The first baroclinic Rossby radius is the ratio of the speed of propagation of long linear internal waves of the lowest mode and the Coriolis parameter. The data from the GDEM V.3.0 climatology for the considered regions are used for calculating internal wave dynamic parameters including wave speed. The seasonal and spatial variability of the baroclinic Rossby radius is discussed in detail. Its magnitudes in the open basins do not exceed 10 km in the Baltic Sea, 20 km in the Black Sea, 18 km in the deep part of the Okhotsk Sea, and 15–18 km in the Mediterranean Sea. Its values decrease 2–5 times in the shelf zones of the seas. Seasonal differences of the baroclinic Rossby radius are studied. The knowledge of the baroclinic Rossby radius makes possible estimating the influence of the Earth's rotation on the internal wave propagation.
Internal wave field in the open seas and oceans is well described by the Garrett-Munk spectrum [Miropolsky, 2001; Morozov, 2018; Pollmann, 2020], but in the shelf zones the spectrum changes. The inertial and tidal waves form peaks in the energy spectrum due to their large lengths and strong currents, but internal waves with higher frequencies and shorter wavelengths are also of great interest [Bulatov and Vladimirov, 2018; Bulatov et al., 2019; Marchenko and Morozov, 2016]. Transformation of very long internal tidal waves in the shelf zones leads to formation of nonlinear internal solitary–like and breather–like waves [Stastna and Lamb, 2002; Talipova et al., 2020], which often have large and anomalous amplitudes. Such waves may damage underwater constructions [Ding et al., 2020; Lin et al., 2019], influence sediment transport [Boegman and Stastna, 2019], and produce acoustic hindrances [Matsui et al., 2019]. Such internal solitary-like or breather-like waves are usually long, especially in the basins with depths shallower than 1 km. Their propagation to the coastal zone can be modeled using the evolution equations of the Korteweg-de Vries hierarchy, such as the combined Korteweg-de Vries equation and the Gardner-Ostrovsky equation [Cai et al., 2002; Grimshaw et al., 2004; Holloway et al., 1999], in which the dispersive and the Earth's rotation speed corrections are small compared to the linear speed of wave propagation. Nonlinear Euler equations are now widely used for modeling of internal waves [Lamb and Warn-Varnas, 2015; Vlasenko and Stashchuk, 2015]. Terms related to the rotation lead to increasing of computer resources. However, the effects of the Earth's rotation on internal wave propagation can be estimated a priori using the magnitude of the baroclinic Rossby radius and comparing it with the distance of wave propagation.
The baroclinic Rossby radius of deformation is the characteristic length scale, which is of fundamental importance in the dynamics of the atmosphere and ocean. Essentially, it is a horizontal scale where rotation effects become as important as buoyancy effects. The baroclinic Rossby radius is a natural scale for the ocean related to such phenomena as boundary currents and fronts, Ekman currents, upwelling, and eddies. Seasonal and interannual variability of this parameter due to the variability of seawater density stratification is a physical mechanism responsible for the variability of the characteristics of the baroclinic modes of Rossby waves. This parameter is very important for understanding the fundamental horizontal scale of mesoscale and submesoscale processes and planning both numerical modelling and in situ studies, in particular, concerning currents and water structure and circulation, e.g. [Frey et al., 2017, 2019; Morozov et al., 2018, 2019].
Analysis of the first baroclinic Rossby radius of deformation was started with the construction of maps of its values in the North Pacific and North Atlantic [Emery et al., 1984], in the South Atlantic [Houry et al., 1987], and in the entire World Ocean [Chelton et al., 1998]. Then, local maps of this parameter based on in situ observations were presented in [Alenius et al., 2003] for the Gulf of Finland in the Baltic Sea, [Osiski et al., 2010] for the South Baltic Sea, [Nurser and Bacon, 2014] for the Arctic Ocean. Averaged and gridded hydrological data were used for the analysis of spatial and monthly variability of the first baroclinic Rossby radius in the South China Sea [Cai et al., 2008]. Saenko [2006] investigated the response of the first baroclinic Rossby radius to the future potential changes in the atmospheric conditions on the basis of 8 general circulation models and found that the zonal-averaged values of this parameter are sensitive to the input hydrological data. Sueyoshi and Yasuda [2009] studied reproducibility and future changes of the first baroclinic Rossby radius from 20 general circulation models. Most of these studies indicate a trend towards an increase in this parameter over the last decades. It is, perhaps, the effect of the global warming. Therefore, the studies of the baroclinic Rossby radius are important.
In this paper, we give a short theoretical background, in which the vertical eigenvalue problem for long internal waves is presented; the first-mode baroclinic speed of propagation, $c$, and the first baroclinic, or internal Rossby radius of deformation $L_{R}$ are calculated for January and July conditions in the Baltic, Black, and Mediterranean seas as well as in the Okhotsk Sea basin. Then, these preliminary estimations can be used as the basic information for numerical modeling aiming at studying the influence of the effect of the Earth's rotation on long short-period localized internal waves (internal solitary-like and breather-like waves).
The internal Rossby radius at a distance from the equator ($|$latitude$| \geq 10\mbox{°}$) is calculated from the following formula:
\begin{equation} \tag*{(1)} L_{R} = c/ |f |, \end{equation}where $f =2 \Omega_{E} \sin \varphi$, $\Omega_{E} = 2 \pi T_{E}$, $T_{E}$ is the period of the Earth's rotation, $\varphi$ is the geographic latitude. Here, internal wave speed $c$ is found as an eigenvalue of the following eigenvalue problem to find the vertical mode function, $\Phi$, and velocity $c$:
\begin{equation} \tag*{(2)} \frac{d^{2} \Phi}{dz^{2}} + \frac{N^{2} (z)}{c^{2}} \Phi =0 \end{equation}with boundary conditions
\begin{equation} \tag*{(3)} \Phi (0) = \Phi (H) = 0, \end{equation}where $z$ is vertical coordinate, ($z = 0$ at the bottom, $z = H$ at the surface); $\Phi (z)$ is the eigenfunction of this problem; it describes the vertical structure of internal wave field; $N(z)$ is the Brunt-Väisälä frequency found from the seawater density $\rho (z)$:
\begin{equation} \tag*{(4)} N^{2} (z) = \frac{g}{\rho (z)} \frac{d\rho (z)}{dz} , \end{equation}where $g$ is acceleration due to gravity, $\rho (z)$ is the vertical profile of seawater density obtained on the basis of hydrological data (profiles of temperature and salinity were taken from the 10-arcminute gridded data of the monthly mean temperature and salinity vertical profiles from GDEM V.3.0 climatology [Carnes, 2009]).
It is important to emphasize that eigenvalue problem (2) and (3) has an infinite number of modes $\Phi_{1} (z), \; \Phi_{2} (z),\ldots ,\Phi_{n} (z),\ldots$ with the respective speeds (eigenvalues) $c_{1} > c_{2} > \ldots > c_{n} > \ldots$ We pay attention to the lowest (first) most energetic mode of internal waves, for which function $\Phi (z)$ has no zeros in the interval between $z = 0$ and $z = H$, and $c$ is the maximum eigenvalue.
Maps of the phase speed $c$ for long internal wave calculated using (2)–(3) can be found in [Kurkina et al., 2011] for the Baltic Sea and in [Kurkina et al., 2015, 2017a] for the Black and Mediterranean seas, and in [Kurkina et al., 2017b] for the Sea of Okhotsk.
 |
| Figure 1 |
Internal Rossby radius, $L_{R}$, and its spatial variability over the Baltic Sea has been determined on the basis of seawater density stratification derived from the GDEM V.3.0 climatology data. In the Baltic Sea (Figure 1), the largest values of $L_{R}$ (about 7–9 km) during all seasons are located in the deep central parts of the Eastern Gotland Basin and in the Bornholm Basin. In the shallow coastal regions and in the gulfs, $L_{R}$ is smaller than in the open deep areas. Average values of $L_{R}$ are 0.5–1 km in the shallow areas (depth $< 50$ m) and 3–5 km in the deeper sea.
The smallest $L_{R}$ values are of the order of a few hundreds of meters, while the largest are over 9 km. The seasonal variability of $L_{R}$ is also well-pronounced. The largest values of Rossby radius over 9 km occur in summer (July) in the Bornholm Basin, when the water density stratification is the strongest, and tend to 8–9 km in winter (January). The data of these calculations are in good agreement with the previous studies in the Baltic Sea [Alenius et al., 2003; Osiski et al., 2010].
 |
| Figure 2 |
Seasonal variability of the first baroclinic Rossby radius is illustrated in Figure 2. In the Baltic Sea (Figure 2), the summer values of this parameter always exceed the values in winter. Seasonal differences are most pronounced at depths up to 100 m and the difference of the values in January and July does not exceed 1.8 km. In the deeper regions, seasonal variations in $L_{R}$ do not exceed 200 m. The most pronounced seasonal variations are observed in the Danish Straits, in the Gulf of Riga, and along the eastern coast of the Baltic Proper.
 |
| Figure 3 |
The dependence of the first baroclinic Rossby radius on the Baltic Sea depth is presented in Figure 3 (left) for the winter time (January). The latitude dependence is evident in the behavior of these data. The Rossby radius is decreasing when latitude becomes higher. First of all, this is because latitude is in the denominator of Eq. (1) for the $L_{R}$. Second, there is a trend to a decrease in long linear internal wave speed of propagation with latitude [Talipova and Polukhin, 2001]. The Rossby radius changes with depth at the same point because stratification is not uniform with depth and also changes seasonally. The variation in the baroclinic Rossby radius $L_{R}$ with sea depth $H$ in July and in January for various latitudes is also shown in Figure 3 (right).
 |
| Figure 4 |
The same procedures were performed for the basins of the Black and Mediterranean seas. Maps of baroclinic Rossby radius $L_{R}$ in the Black and Mediterranean seas calculated for January (top) and July (bottom) are presented in Figure 4. As for the Mediterranean Sea basin, typical values of the first baroclinic Rossby radius here fall within the range 5–15 km. The largest values of $L_{R}$ were observed in the Black Sea, in its southern and eastern parts, and in the southeastern parts of the Libyan Sea, north of the Gulf of Sidra, and, in January, at the northern coasts of the Ligurian Sea. The values of $L_{R}$ tend to 15 km in the middle, eastern, and southern parts of the Black Sea due to the strong stratification together with the extreme linear velocity of propagation of internal waves, $c$, reaching 1.5 m/s and greater in these zones [Kurkina et al., 2017a].
 |
| Figure 5 |
In the Mediterranean basin, seasonal changes in the first baroclinic Rossby radius may lead either to greater or smaller values of the radius. (Figure 5). Summer values are generally higher than those in winter, but at some locations $L_{R}$ in January is larger than in July. This trend is especially strong in the Ligurian Sea (up to 9 km difference) and in the southern part of the Gulf of Lion. The values in July significantly exceed (up to 5–8 km) the values in January along the southern coast of the Mediterranean Sea, in the Myrtoan Sea and in the Thracian Sea, as well as in the Adriatic Sea.
 |
| Figure 6 |
Dependence of the internal Rossby radius on depth in the Mediterranean basin is shown in Figure 6. In the Mediterranean Sea the latitudes change from 30° N to 41° N and the baroclinic Rossby radius decreases with increasing latitude similarly to the Baltic Sea. The measured values for each latitude here may be approximated by the curve, which sharply increases from zero to a depth of about 1 km and tends to constant or weakly increases with the further depth increase. The measured values appear located lower and lower with increasing latitude and the lowest values (yellow points) correspond to a latitude of 41° N. The values corresponding to the Black Sea begin from a latitude of 41.5° (yellow points); they are located higher than those in the Mediterranean Sea, because the speed of internal wave propagation here is larger than in the Mediterranean. The decreasing trend of the Rossby radius with latitude is also valid in the Black Sea (red points at a latitude of 45°). The difference between baroclinic Rossby radius $L_{R}$ as functions of the sea depth $H$ in July and in January in the Mediterranean and Black seas is also shown on Figure 6. The large negative values shown by yellow and red points belong to the Ligurian Sea data.
Estimations of the first baroclinic Rossby radius in the Okhotsk Sea were recently given in [Stepanov, 2017] based on the data from database WOA 2001 and WOA 2013.
The speed of internal wave propagation in [Stepanov, 2017] was calculated from the expression
\begin{equation} \tag*{(5)} c \approx \frac{1}{\pi } \int_{-H}^{0} N(z) dz \end{equation}if $N(z)$ slowly changes in the vertical direction. Estimates of c were computed numerically from the eigenvalue problem only when $N(z)$ was strongly changing with depth. We used the GDEM V.3.0 climatology data to build the maps of the internal Rossby radius and calculate linear long internal wave speeds $c$ numerically using problem (2)–(4). We focus on the shallow zones because the underwater constructions are located exactly in the shallow depth regions, and numerical modeling of internal wave propagation is important here.
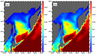 |
| Figure 7 |
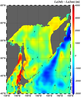 |
| Figure 8 |
The maps of the baroclinic Rossby radius for the Sea of Okhotsk are shown in Figure 7 for the summer and winter periods. In the deepest part of the Okhotsk Sea (the Kuril Deep) and nearest areas of the Pacific, the values of $L_{R}$ are in the range of 15–20 km in all seasons. In [Stepanov, 2017] the same ranges of values are shown. The values are also close for the Deryugin Deep; they are about 8–10 km. In the shallow zones, the values of the first baroclinic Rossby radius are very sensitive to the season. It is clearly seen from Figure 8, where the difference between baroclinic Rossby radius $L_{R}$, in July and in January in the Okhotsk Sea is shown. There is almost no difference in the major part of the Kuril Deep and in the large western part of the Deryugin Deep, and the difference in $L_{R}$ is smaller than 1 km in the other deep regions of the sea.
The difference in the Rossby radius increases up to 2 km in nearshore zones, in which the depth is shallower than a few hundred meters, especially near Sakhalin Island and Kamchatka (up to 3 km). These zones have strong seasonal changes in stratification [Kurkina et al., 2017b] due to heating in summer, which influences the buoyancy frequency profile and speed of internal wave propagation.
 |
| Figure 9 |
The dependence of the first baroclinic Rossby radius on the depth in the Sea of Okhotsk is presented in Figure 9 (left) in winter (January). Its behavior is similar to the patterns in other seas. The Rossby radius values tend to decrease with increasing latitude. In this figure we can also see that the values in the Sea of Okhotsk and those in the Japan Sea are separated with different trends with depth. The cluster of points of measurements corresponding to the Sea of Japan is located much lower. The values estimated for the Pacific Ocean are truncated by the restriction of the horizontal axis. The differences between baroclinic Rossby radius $L_{R}$ as functions of depth $H$ in July and in January at various latitudes are shown in Figure 9 (right). These differences do not exceed 4 km, and the values mainly tend to decrease at higher latitudes.
Due to the regional variations in depth, stratification, and latitude, $L_{R}$ varies strongly in different regions. The values of $L_{R}$ in the open sea do not exceed 10 km in the Baltic Sea, 20 km in the Black Sea, 15–18 km in the Mediterranean Sea and the Okhotsk Sea in all seasons. In the shelf zones of these seas, the values of $L_{R}$ are much smaller. The seasonal variability impacts strongly the first baroclinic Rossby radius mainly in the shallow and coastal regions. In the deep-sea regions, the effect of seasonal changes of stratification on $L_{R}$ can be neglected. The largest difference between July and January values of $L_{R}$ reach 1.9 km in the Baltic Sea, $-9.9$ km and $+8$ km in the Mediterranean basin, about 3 km in the Black Sea, and about 4 km in the Okhotsk Sea.
The first baroclinic Rossby radius has a tendency to decrease with increasing latitude in each individual sea. But in the different seas, the hydrological features of stratification can lead to deviations from this trend. For example, in the deeper parts of the southern Mediterranean Sea and northern Sea of Okhotsk, close values of the Rossby radius (15–20 km) are observed. Thus, the value of 20 km can be taken as the upper boundary of the Rossby radius in theses seas. It means, for the modeling of transformation of the first-mode internal waves over the distances longer than this value one should take into account the effects of the Earth's rotation.
Alenius, P., A. Nekrasov, K. Myrberg (2003) , Variability of the baroclinic Rossby radius in the Gulf of Finland, Continental Shelf Research, 23, no. 6, p. 563–573, https://doi.org/10.1016/S0278-4343(03)00004-9.
Boegman, L., M. Stastna (2019) , Sediment resuspension and transport by internal solitary waves, Annual Review of Fluid Mechanics, 51, p. 129–154, https://doi.org/10.1146/annurev-fluid-122316-045049.
Bulatov, V. V., Yu. V. Vladimirov (2018) , Unsteady regimes of internal gravity wave generation in the ocean, Russ. J. Earth Sci., 18, no. 2, p. ES2004, https://doi.org/10.2205/2018ES000619.
Bulatov, V. V., Y. V. Vladimirov, I. Y. Vladimirov (2019) , Far fields of internal gravity waves from a source moving in the ocean with an arbitrary buoyancy frequency distribution, Russ. J. Earth Sci., 19, p. ES5003, https://doi.org/10.2205/2019ES000667.
Cai, Sh., X. Long, Z. Gan (2002) , A numerical study of the generation and propagation of internal solitary waves in the Luzon Strait, Oceanologica Acta, 25, p. 51–60, https://doi.org/10.1016/S0399-1784(02)01181-7.
Cai, S., X. Long, R. Wu, et al. (2008) , Geographical and monthly variability of the first baroclinic Rossby radius of deformation in the South China Sea, Journal of Marine Systems, 74, no. 1–2, p. 711–720, https://doi.org/10.1016/j.jmarsys.2007.12.008.
Carnes, M. R. (2009) , Description and evaluation of GDEM-V3.0, NRL Rep. NRL/MR/7330-09-9165, Nav. Res. Lab., Washington, D. C.
Chelton, D. B., R. A. deSzoeke, M. G. Schlax, et al. (1998) , Geographical Variability of the First Baroclinic Rossby Radius of Deformation, J. Phys. Oceanogr., 28, p. 433–460, https://doi.org/10.1175/1520-0485(1998)028%3C0433:GVOTFB%3E2.0.CO;2.
Ding, W., C. Ai, S. Jin, et al. (2020) , 3D Numerical Investigation of Forces and Flow Field around the Semi-Submersible Platform in An Internal Solitary Wave, Water, 12, no. 1, p. 208, https://doi.org/10.3390/w12010208.
Emery, W. J., W. G. Lee, L. Magaard (1984) , Geographical and seasonal distribution of Brunt-Vaisala frequency and Rossby radii in the North Pacific and North Atlantic, J. Phys. Oceanogr., 14, p. 294–317.
Frey, D. I., A. N. Novigatsky, M. D. Kravchishina, et al. (2017) , Water structure and currents in the Bear Island Trough in July–August 2017, Russ. J. Earth. Sci., 17, p. ES3003, https://doi.org/10.2205/2017ES000602.
Frey, D. I., E. G. Morozov, I. Ansorge, et al. (2019) , Thermohaline structure of Antarctic Bottom Water in the abyssal basins of the South Atlantic, Russ. J. Earth Sci., 19, p. ES5005, https://doi.org/10.2205/2019ES000679.
Holloway, P., E. Pelinovsky, T. Talipova (1999) , A Generalized Korteweg-de Vries Model of Internal Tide Transformation in the Coastal Zone, J. Geophys. Res., 104, no. C8, p. 18333–18350, https://doi.org/10.1029/1999JC900144.
Houry, S., E. Dombrovsky, P. DeMey, et al. (1987) , Brunt–Väisälä frequency and Rossby radii in the South Atlantic, J. Phys. Oceanogr., 17, p. 1619–1626, https://doi.org/10.1175/1520-0485(1987)017%3C1619:BVFARR%3E2.0.CO;2.
Grimshaw, R., E. Pelinovsky, T. Talipova, et al. (2004) , Simulation of the transformation of internal solitary waves on oceanic shelves, J. Phys. Oceanogr., 34, p. 2774–2791, https://doi.org/10.1175/JPO2652.1.
Kurkin, A., O. Kurkina, T. Talipova, et al. (2015) , Internal waves in the Mediterranean Sea: mapping and transformations, E. Ozhan (ed.), Proceedings of the Twelfth International Conference on the Mediterranean Coastal Environment, MEDCOAST 15, 06–10 October 2015, Varna, Bulgaria, vol. 2, p. 835–846, MEDCOAST Mediterranean Coastal Foundation, Dalyan, Mugla, Turkey.
Kurkina, O., E. Pelinovsky, et al. (2011) , Mapping the internal wave field in the Baltic Sea in the context of sediment transport in shallow water, J. Coast. Res., no. SI 64, p. 2042–2047.
Kurkina, O., E. Rouvinskaya, et al. (2017a) , Propagation regimes and populations of internal waves in the Mediterranean Sea basin, Estuarine, Coastal and Shelf Science, 185, p. 44–54, https://doi.org/10.1016/j.ecss.2016.12.003.
Kurkina, O., T. Talipova, et al. (2017b) , The impact of seasonal changes in stratification on the dynamics of internal waves in the Sea of Okhotsk, Estonian Journal of Earth Sciences, 66, no. 4, p. 238–255, https://doi.org/10.3176/earth.2017.20.
Lamb, K. G., A. Warn-Varnas (2015) , Two-dimensional numerical simulations of shoaling internal solitary waves at the ASIAEX site in the South China Sea, Nonlin. Processes Geophys., 22, p. 289–312, https://doi.org/10.5194/npg-22-289-2015.
Lin, Q., X. G. Du, J. Kuang, et al. (2019) , Forces and moments exerted by incident internal waves on a plate-cylinder structure in a two-layer fluid, Meccanica, 54, no. 10, p. 1545–1560, https://doi.org/10.1007/s11012-019-01032-0.
Marchenko, A. V., E. G. Morozov (2016) , Surface manifestations of the waves in the ocean covered with ice, Russ. J. Earth Sci., 16, no. 1, p. ES1001, https://doi.org/10.2205/2016ES000561.
Matsui, R., M. Kido, Y. Niwa, et al. (2019) , Effects of disturbance of seawater excited by internal wave on GNSS-acoustic positioning, Marine Geophysical Research, 40, no. 4, p. 541–555, https://doi.org/10.1007/s11001-019-09394-6.
Miropolsky, Yu. Z. (2001) , Dynamics of internal gravity waves in the ocean, 321 pp., Springer, Dordrecht, https://doi.org/10.1007/978-94-017-1325-2.
Morozov, E. G. (2018) , Oceanic internal tides. Observations, analysis and modeling, 304 pp., Springer, Cham, https://doi.org/10.1007/978-3-319-73159-9.
Morozov, E. G., R. Yu. Tarakanov, D. I. Frey, et al. (2018) , Currents and water structure north of the Vema Channel, Russ. J. Earth Sci., 18, p. ES5006, https://doi.org/10.2205/2018ES000630.
Morozov, E. G., D. I. Frey, N. A. Diansky, et al. (2019) , Bottom circulation in the Norwegian Sea, Russ. J. Earth Sci., 19, p. ES2004, https://doi.org/10.2205/2019ES000655.
Nurser, A. J. G., S. Bacon (2014) , The Rossby radius in the Arctic Ocean, Ocean Science, 10, no. 6, p. 967–975, https://doi.org/10.5194/os-10-967-2014.
Osiski, R., D. Rak, W. Walczowski, et al. (2010) , Baroclinic Rossby radius of deformation in the southern Baltic Sea, Oceanologia, 52, no. 3, p. 417–429, https://doi.org/10.5697/oc.52-3.417.
Pollmann, F. (2020) , Global characterization of the ocean's internal wave spectrum, Journal of Physical Oceanography, 50, no. 7, p. 1871–1891, https://doi.org/10.1175/JPO-D-19-0185.1.
Saenko, O. A. (2006) , Influence of Global Warming on Baroclinic Rossby Radius in the Ocean: A Model Intercomparison, Journal of Climate, 19, no. 7, p. 1354–1360, https://doi.org/10.1175/JCLI3683.1.
Stastna, M., K. Lamb (2002) , Large fully nonlinear internal solitary waves: The effect of background current, Physics of Fluids, 14, no. 9, p. 2987–2999, https://doi.org/10.1063/1.1496510.
Stepanov, D. V. (2017) , Estimating the baroclinic Rossby radius of deformation in the Sea of Okhotsk, Russian Meteorology and Hydrology, 42, no. 9, p. 601–606, https://doi.org/10.3103/S1068373917090072.
Sueyoshi, M., T. Yasuda (2009) , Reproducibility and Future Projection of the Ocean First Baroclinic Rossby Radius Based on the CMIP3 Multi-Model Dataset, Journal of the Meteorological Society of Japan. Ser. II, 87, no. 4, p. 821–827, https://doi.org/10.2151/jmsj.87.821.
Talipova, T., N. Polukhin (2001) , Averaged characteristics of the internal wave propagation parameters in the World Ocean, Izvestia of Russian Academy of Engineering Sciences, Series: Applied Mathematics and Informatics, 2, p. 139–155 (in Russian).
Talipova, T., O. Kurkina, A. Kurkin, et al. (2020) , Internal Wave Breathers in the Slightly Stratified Fluid, Microgravity Science and Technology, 32, p. 69–77, https://doi.org/10.1007/s12217-019-09738-2.
Vlasenko, V., N. Stashchuk (2015) , Internal tides near the Celtic Sea shelf break: A new look at a well known problem, Deep-Sea Res. I, 103, p. 24–36, https://doi.org/10.1016/j.dsr.2015.05.003.
Received 8 June 2020; accepted 12 June 2020; published 12 July 2020.


Citation: Kurkin
A., O. Kurkina, A. Rybin, T. Talipova (2020), Comparative
analysis of the first baroclinic Rossby radius in the Baltic,
Black, Okhotsk, and Mediterranean seas, Russ. J. Earth Sci.,
20, ES4008, doi:10.2205/2020ES000737.
Copyright 2020 by the Geophysical Center RAS.