RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 20, ES4004, doi:10.2205/2020ES000732, 2020
V. V. Bulatov, Yu. V. Vladimirov
Ishlinsky Institute for Problems in Mechanics RAS, Moscow, Russia
The problem of the harmonic internal gravity wave dynamics in a stratified ocean of finite depth with shear flows is solved. Stratification with constant distribution of the buoyancy frequency and various linear dependences of the shear flow on depth were used for the analytical solution of the problem. Dispersion dependences were obtained, which are expressed through a modified Bessel function of an imaginary index. The Debye asymptotics of the modified Bessel function of the imaginary index were used to construct analytical solutions under the Miles stability condition and large Richardson numbers. The asymptotic properties of the dispersion equation are studied. The main analytical properties of dispersion curves are investigated. The results of numerical calculations of the fields of phase structures of the generated internal gravity waves for various models of wave generation are presented.
Among the large variety of observed wave processes of different physical nature in the ocean and the Earth's atmosphere, the interaction between generated waves and hydrodynamic flows is of particular interest [Fabrikant and Stepanyants, 1998; Miropol'skii, 2001; Morozov, 2018; Mei et al., 2017; Velarde et al., 2018]. The motion in a stratified medium is one of the main factors that influence the dynamics of internal gravity waves (IGW) both under natural conditions and in technical devices. In the current scientific research, asymptotic methods for studying analytic models of wave generation are used to analyze the dynamics of IGW in natural stratified media with the presence of currents. In the linear approximation, the existing approaches to describing the wave pattern of the generated IGW fields are based on the representation of wave fields by Fourier integrals and their asymptotic analysis [Bulatov and Vladimirov, 2012, 2019]. When studying the real ocean environment, it is necessary to consider the IGW propagating against the background of mean currents with a vertical velocity shear; the variations in the vertical speed are tens of cm/s and m/s, that is, they are of the same order as the maximum IGW speeds. Such flows must significantly influence the IGW propagation [Massel, 2015; Pedlosky, 2010; Sutherland, 2010]. If the scale of variations in the horizontal flows is much larger than the length of IGW and the scale of time variations is much larger than the periods of internal waves, then a natural mathematical model represents the case of stationary and horizontal homogeneous shear flows [Fabrikant and Stepanyants, 1998; Fraternale et al., 2018; Miropol'skii, 2001]. The goal of this work is to construct analytic solutions describing the IGW fields in a stratified medium of finite depth with shear flows.
We consider a vertically stratified medium of finite depth $H$. Let $(U(z),V(z))$ be the vector of shear flow at depth $z$. The further analysis starts from the linearized system of hydrodynamic equations for the unperturbed state; the system has the form [Bulatov and Vladimirov, 2019; Fabrikant and Stepanyants, 1998; Miles, 1961; Miropol'skii, 2001]
\begin{eqnarray*} \rho_{0} \frac{DU_{1}}{Dt} + \frac{\partial p}{\partial x} =0, \quad \rho_{0} \frac{DU_{2}}{Dt} + \frac{\partial p}{\partial y} = 0, \end{eqnarray*} \begin{eqnarray*} \rho_{0} \frac{DW}{Dt} + \frac{\partial p}{\partial z} + \rho g = 0, \end{eqnarray*} \begin{eqnarray*} \frac{\partial U_{1}}{\partial x} + \frac{\partial U_{2}}{\partial y} + \frac{\partial W}{\partial z} = 0, \quad \frac{\partial \rho }{\partial t} + W\frac{\partial \rho_{0} }{\partial z} = 0, \end{eqnarray*} \begin{eqnarray*} \frac{D}{Dt} = \frac{\partial}{\partial t} + U(z) \frac{\partial}{\partial x} + V(z)\frac{\partial}{\partial y}, \end{eqnarray*}where ($U_{1}$, $U_{2}$, $W$) are components of the perturbed velocity, $(p, \rho$) are perturbations of the pressure and density, and $\rho_{0} (z)$ is the unperturbed density of the medium. Using the Boussinesq approximation, one can obtain the equation for the vertical component of velocity [Bulatov and Vladimirov, 2012, 2019]
\begin{eqnarray*} \frac{D^{2}}{Dt^{2}} \Delta W - \frac{D}{Dt} (\frac{d^{2} U}{dz^{2}} \frac{\partial W}{\partial x} + \frac{d^{2} V}{dz^{2}} \frac{\partial W}{\partial y}) + \end{eqnarray*} \begin{equation} \tag*{(1)} N^{2} (z) \Delta_{2} W = 0, \end{equation} \begin{eqnarray*} \Delta = \Delta_{2} + \frac{\partial^{2}}{\partial z^{2}}, \quad \Delta_{2} = \frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}}, \end{eqnarray*} \begin{eqnarray*} N^{2} (z) = -\frac{g}{\rho_{0} (z)} \frac{d\rho_{0} (z)}{dz}, \end{eqnarray*}where $N^{2} (z)$ is the squared Brunt-Vaisala frequency (buoyancy frequency) and $g$ is the acceleration due to gravity. The boundary conditions are taken in the form (the vertical axis $Z$ is directed upward)
\begin{equation} \tag*{(2)} W=0 \mbox{ at } z=0,-H. \end{equation}We further use the following assumptions. The Brunt-Vaisala frequency is assumed to be constant: $N(z)= N = $ const. The shear flow is assumed to be one-dimensional: $V(z)\equiv 0$. The function $U(z)$ is a linear function of depth: $U(z) = U_{0} + (U_{0} - U_{H}) z/H$, $U_{0} = U(0) > 0$, $U_{H} = U(-H) <0$. This hydrology model (constant distribution of buoyancy frequency, multidirectional shear flows) is widely used in real oceanological calculations and allows one to take into account the main features of wave dynamics with regard to the real variations in the density of the marine environment observed in full-scale measurements of IGW in the ocean, as well as to investigate the problem analytically [Velarde et al., 2018]. The results of numerous studies of natural measurements of internal waves, flows, and their interaction in various regions of the World Ocean were analyzed in [Frey et al., 2017; Mei et al., 2017; Morozov, 2018], in particular, by using this model. The generation of IGW by a shear current in the Kara Gates Strait was considered in [Morozov, 2003, 2008, 2017]; in this case, the flow fluctuates with the tidal frequency, and the IGW packets appear at intervals determined by the shear instability of flows. Similar results were obtained in [Morozov, 2018] using the example of the Strait of Gibraltar, where the measurements of flows and IGW whose amplitude can be tens of meters are considered. Numerous measurements of bottom flows in deep waters of the North Atlantic show that, at high depths, the gradients of shear velocities and the buoyancy frequency values are small and the main variations in these hydrophysical parameters are observed in the upper layers of the ocean at depths of about 100–200 meters, which allows one to use the proposed hydrology model and the linear dependence of shear flows on the depth [Frey et al., 2017]. We also assume that the Miles stability conditions are satisfied for the Richardson number:
\begin{eqnarray*} Ri=N^{2} (\frac{dU}{dz})^{-2} > \frac{1}{4} \end{eqnarray*}[Fabrikant and Stepanyants, 1998; Miles, 1961; Miropol'skii, 2001]. The characteristic values of the Richardson numbers in the waters of the World Ocean (Atlantic Ocean, Arctic basin seas) in the absence of dynamic instability of flows range from 2 to 20 [Velarde et al., 2018]. Then Eqs. (1)–(2) can be represented in dimensionless variables
\begin{eqnarray*} x^* = \pi x/H,\quad y^* = \pi y/H,\quad z^* = \pi z/H, \end{eqnarray*} \begin{eqnarray*} \omega^* = \omega /N, \quad t^* = tN, \end{eqnarray*} \begin{eqnarray*} M( z^* )= U(z) \pi/ NH = a + b z^* \end{eqnarray*} \begin{eqnarray*} a = \pi U_{0} / NH, \quad b=(U_0 - U_H ) / NH \end{eqnarray*}in the form (asterisks "*" are omitted)
\begin{equation} \tag*{(3)} (\frac{\partial}{\partial t} + M(z) \frac{\partial}{\partial x})^{2} \Delta W + N^{2} (z) \Delta_{2} W = 0, \end{equation} \begin{eqnarray*} W = 0 \mbox{ at } z = 0,-\pi . \end{eqnarray*}The above-introduced parameter $b$ is the inverse square root of the Richardson number: $b = 1/\sqrt{Ri}$, and parameter $a$ is the ratio of the near-surface flow amplitude $U_{0}$ to the maximum group velocity of IGW propagation in the ocean, equal to $NH/\pi$ [Bulatov and Vladimirov, 2012, 2019].
We seek the solution of problem (3) in the form of harmonic waves: $W (t,x,y,z) = \varphi (z) \exp (i (\omega t - \mu x - \nu y)$. Then to determine the function $\varphi (z)$, we have
\begin{equation} \tag*{(4)} \frac{\partial^{2} \varphi}{\partial z^{2}} + k^{2} ((\omega -\mu M(z))^{-2} -1) \varphi = 0, \end{equation}$\varphi = 0$ for $z = 0,-\pi $, $k^{2} = \mu^{2} + \nu^{2} $.
We assume that two linearly independent solutions of problem (4) exist
\begin{eqnarray*} f_{\pm } (z) = \sqrt{2\beta r(z)} I_{\pm i\lambda} (\beta r(z)), \end{eqnarray*}where $I_{\pm i\lambda}$ is the modified Bessel function with imaginary index $i\lambda$, $r(z) = \omega -\mu M(z)$,
$\lambda =\sqrt{\beta^{2} - 1/4}$, $\beta = k/b \mu $. The solution satisfying the condition at $z = 0$ becomes: $\varphi (z) =i (f_+ (0) f_- (z) -f_- (0)f_+ (z))$. The functions $f_{\pm } (z)$ are complex conjugate, and hence the solution $\varphi (z)$ is real. Since we assume that the Miles stability condition is satisfied for the large Richardson numbers, we have $b^{2} < 4$. In particular, this implies that $\beta^2 > 1/4$, and hence the values of $\lambda$ are real. The requirement to satisfy the boundary condition at $z = -\pi$ determines the dispersion relation
\begin{eqnarray*} I_{i\lambda} (\beta r(0)) I_{-i\lambda} (\beta r(-\pi)) - \end{eqnarray*} \begin{equation} \tag*{(5)} I_{-i\lambda} (\beta r(0))I_{i\lambda} (\beta r(-\pi )) = 0. \end{equation}The dispersion relation for a similar hydrology model (constant buoyancy frequency, linear profile of the shear flow, the finite thickness of a stratified layer) is obtained in [Gavrileva et al., 2019] in the form similar to (5), and it was noted that to obtain a solution of this equation is a difficult mathematical problem. A more difficult problem is to study the analytical properties of the obtained dispersion equation, since this allows one to obtain asymptotic expressions for the IGW fields under different modes of wave generation. Further, we will study the main characteristic features of solutions of dispersion equation (5) and construct asymptotic representations of the solution of this equation. The solutions of this equation can be represented in the form $\omega_{n} (\mu ,\nu)$ or $\mu_{n} (\nu ,\omega)$. In this paper, we study the dispersion dependence $\mu_{n} (\nu )$ (here $\omega$ is a fixed parameter) for $\omega = 0.54$, $a = 0.8$. In the model of shear flows, we take $a < 1$ which means that the amplitudes of shear flows do not exceed the maximum group velocity of IGW propagation, which is observed under the real conditions in the World Ocean. Parameter $\omega < 1$ determines the ratio of the free wave frequency to the maximum value of the buoyancy frequency and describes the IGW propagation with a frequency almost two times smaller than the buoyancy frequency, and this phenomenon is also observed in the real ocean environment [Mei et al., 2017; Morozov, 2018; Velarde et al., 2018].
Starting from numerous results of oceanological observations of shear flows in the waters of the World Ocean, we can consider three model distributions of one-dimensional shear flow [Frey et al., 2017; Morozov, 2018; Velarde et al., 2018]. In this paper, we use the hydrology model of linear shear flow including the possibility that the flow changes its direction as the depth increases.
 |
| Figure 1 |
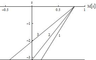
The first model: Unidirectional flow, the flow does not change its direction with increasing depth, the flow amplitude decreases with depth, but at the bottom, the amplitude of the bottom flow is different from zero $U_{H} \ne 0$ (line 1 in Figure 1).
The second model: Unidirectional flow, the flow amplitude decreases with depth, and the amplitude of the bottom flow is small as compared to the amplitude of the near-surface flow $U_{H} =0$ (line 2 in Figure 1).
The third model: Multidirectional flows, the flow changes its direction with increasing depth, the amplitude of the bottom flow is comparable in order with the amplitude of the near-surface flow (line 3 in Figure 1). We use parameters $b = 0.2$, $Ri = 25$ for the first model, $b = a/\pi$, $Ri = 15.3$ for the second model, and $b = 0.39$, $Ri = 6.5$ for the third model.
We consider the asymptotic solutions of dispersion equation (5) under the assumption that parameter $\beta$ is large; then $\lambda$ can be replaced by $|\beta|$. We use the Debye asymptotics $(\lambda \gg 1)$ of the modified Bessel function with imaginary index $I_{\pm i\lambda } (\tau)$ which, in contrast to the classical asymptotics as $\tau \to \infty$, determines the behavior of the function $I_{\pm i\lambda} (\tau)$ for large values of both index $\lambda$ and argument $\tau$. The modified Bessel function $I_{\pm i\lambda} (\tau)$ satisfies the equation [Watson, 1995]
\begin{eqnarray*} \tau^{2} Y"(\tau ) + \tau Y(\tau ) + (\lambda^{2} -\tau^{2}) Y(\tau ) = 0, \end{eqnarray*} \begin{eqnarray*} Y(\tau) = I_{\pm i\lambda} (\tau). \end{eqnarray*}Using the change of variable $Y(\tau) = Z(\tau)/\sqrt{\tau}$, we can represent this equation in the form
\begin{equation} \tag*{(6)} Z"(\tau ) + (1/4 + \lambda^{2} - \tau^{2})\tau^{-2} Z(\tau ) = 0. \end{equation}For $\lambda \gg 1/4$, Eq. (6) becomes simpler
\begin{eqnarray*} Z"(\tau ) + q(\tau ) Z(\tau) = 0, \end{eqnarray*} \begin{equation} \tag*{(7)} q(\tau) = (\lambda^{2} - \tau^{2})\tau^{-2} . \end{equation}Then the WKB asymptotics of Eq. (7) for $\tau < \lambda$, which describes the oscillating solutions, becomes
\begin{eqnarray*} Z(\tau) \approx q(\tau )^{-1/4} \exp (i\int \sqrt{q(\tau)} d\tau) , \end{eqnarray*} \begin{eqnarray*} \int \sqrt{q(\tau)} d\tau = \sqrt{\lambda^{2} -\tau^{2}} - \frac{\lambda}{2} \ln \frac{\lambda + \sqrt{\lambda}^{2} - \tau^{2}}{\lambda -\sqrt{\lambda^{2} - \tau^{2}}} \end{eqnarray*}For exponentially increasing or decreasing solutions, the WKB asymptotics of Eq. (7) for $\tau > \lambda$ becomes
\begin{eqnarray*} Z(\tau ) \approx D_{\pm} (-q(\tau))^{-1/4} \exp (i\int \sqrt{-q(\tau)} d\tau) , \end{eqnarray*} \begin{eqnarray*} \int \sqrt{-q(\tau)} d\tau = \sqrt{\tau^{2} - \lambda^{2}} - \end{eqnarray*} \begin{eqnarray*} \lambda \arctan (\sqrt{\tau^{2} -\lambda^{2}} /\lambda) . \end{eqnarray*}Further, we consider only function $I_{-i\lambda} (\tau)$ (the function $I_{-i\lambda} (\tau)$ is the complex conjugate of $I_{i\lambda} (\tau)$ and $I_{i\lambda} (-\tau ) = \exp (-\pi \lambda) I_{i\lambda} (\tau )$). To determine the multipliers $D_{\pm}$, it is required to compare the WKB asymptotics with the classical asymptotics of $I_{-i\lambda} (\tau)$ as $\tau \to \infty $
\begin{eqnarray*} \mathrm{Re}\, I_{-i\lambda} (\tau) \approx \exp (\tau ) /\sqrt{2\pi \tau}, \end{eqnarray*} \begin{eqnarray*} \mathrm{Im} \,I_{-i\lambda} (\tau ) \approx \exp (-\tau +\pi \lambda)/2\sqrt{2\pi \tau} \end{eqnarray*}The expression for the WKB asymptotics of function $I_{-i\lambda} (\tau )$ for $\tau > \lambda$ has the form
\begin{eqnarray*} \mathrm{Re} \,I_{-i\lambda} (\tau ) \approx (\tau^{2} -\lambda^{2} )^{-1/4} \exp (\Lambda_{+}) / \sqrt{2\pi } , \end{eqnarray*} \begin{equation} \tag*{(8)} \mathrm{Im}\, I_{-i\lambda} (\tau ) \approx (\tau^{2} -\lambda^{2})^{-1/4} \exp (\Lambda_{-} ) / 2\sqrt{2\pi} , \end{equation} \begin{eqnarray*} \Lambda_{\pm } = \pm \sqrt{\tau^{2} -\lambda^{2} } \:\mp \end{eqnarray*} \begin{eqnarray*} \lambda \arctan (\sqrt{\tau^{2} - \lambda^{2}} / \lambda ) + \pi \lambda /2. \end{eqnarray*}We analytically continue the first formula in (8) from the domain $\tau > \lambda$ in the domain $\tau < \lambda$ through the upper half-plane of the complex variable $\tau$ and, as a result, we obtain
\begin{equation} \tag*{(9)} I_{-i\lambda} (\tau) \approx (\tau^{2} -\lambda^{2})^{-1/4} \exp (\alpha )/\sqrt{2\pi } , \end{equation} \begin{eqnarray*} \alpha = -i (\sqrt{\lambda^{2} - \tau^{2}} - \end{eqnarray*} \begin{eqnarray*} \frac{\lambda }{2} \ln \frac{\lambda + \sqrt{\lambda^{2} -\tau^{2}}}{\lambda -\sqrt{\lambda^{2} - \tau^{2}}} - \pi/4) + \pi \lambda /2. \end{eqnarray*}Then the Debye asymptotics of the modified Bessel function $I_{-i\lambda} (\tau)$ with imaginary index (for large values of both index $\lambda$ and argument $\tau$) is obtained by substituting $\lambda r$ in (8) and (9) instead of $\tau$ [Watson, 1995]
\begin{eqnarray*} I_{-i\lambda} (\lambda r) \approx (r^{2} -1)^{-1/4} \times \end{eqnarray*} \begin{equation} \tag*{(10)} \exp (\pm i(\lambda \Theta -\pi /4) \exp (\pi \lambda /2)/ \sqrt{2\pi \lambda} , \end{equation} \begin{eqnarray*} \Theta = \sqrt{1-r^{2}} - \frac{1}{2} \ln \frac{1 + \sqrt{1 -r^{2}}}{1 - \sqrt{1 -r^{2}}}), \quad 0< r < 1, \end{eqnarray*} \begin{eqnarray*} \mathrm{Re} \,I_{\pm i\lambda} (\lambda r) \approx (r^{2} - 1)^{-1/4} \times \end{eqnarray*} \begin{eqnarray*} \exp (\lambda (\Phi(r) + \pi / 2))/ \sqrt{2\pi \lambda } , \end{eqnarray*} \begin{equation} \tag*{(11)} \mathrm{Im} \,I_{\pm i\lambda } (\lambda r)\approx \mu (r^{2} -1)^{-1/4} \times \end{equation} \begin{eqnarray*} \exp (-\lambda (\Phi(r) - \pi /2))/2\sqrt{2\pi \lambda} \end{eqnarray*} \begin{eqnarray*} \Phi(r) = \sqrt{r^{2} -1} -\arctan (\sqrt{r^{2} -1}), \quad r>1. \end{eqnarray*}The value $r = 0$ is a branch point, and $ r = 1$ is the turning point at which the asymptotics (10), (11) do not work. If $r < 0$, then $I_{i\lambda} (\lambda r) = \exp (-\pi \lambda)I_{i\lambda} (-\lambda r)$, $I_{-i\lambda} (\lambda r) = \exp (\pi \lambda)I_{-i\lambda } (-\lambda r)$.
 |
| Figure 2 |
Figure 2 illustrates the geometry of location of singular points, which determines the main qualitative characteristics of the behavior of dispersion curves on the plane of variables ($\Psi$, $\mu$), where $\Psi = \omega -\mu M(z)$. Figure 2 shows $r(0)$ (line 1) and $r(-\pi)$ (line 2) as functions of $\mu$ for all three models. The points $a$ and $d$ are branch points; they correspond to the values of $\mu$ at which $r (0) = r(-\pi) = 0$, and for the second model, there exists only one branch point $d$. The cuts on the complex plane of the variable $\mu$ are drawn in the intervals of the axis $Re\mu$, where $r(0)r(-\pi ) < 0$. In the first model, the cuts on the complex plane $\mu$ pass from $a$ to $d$, for the second model, the cuts pass from the point $d$ to $+\infty$, and for the third model, the cuts pass from $-\infty$ to point $a$ and from the point $d$ to $+\infty$. The points $b,c,e,f$ (the first and second models) are turning points and determine the values of the variable $\mu$ for which the wave solution exists, i.e., these are the points at which $|r(0)| =|r(-\pi)| = 1$. For the second model, the turning points are $b,f$.
In dispersion equation (5), the first and second terms are complex conjugate, and hence this equation can be represented as
\begin{equation} \tag*{(12)} \mathrm{Im} (I_{i\beta} (\beta r(0)) I_{-i\beta } (\beta r(-\pi ))) = 0. \end{equation}Difficulties in obtaining numerical solutions of dispersion equation (12) arise due to the fact that the eigenvalues have accumulation points as $\nu \to 0$; these points are branch points (points $a$ and $d$ in Figure 2), and in the first model as $\nu \to \infty$, these are also turning points (points $\mu_{c} $ and $\mu_{e}$). Therefore, we further solve Eq. (12) asymptotically for the three models of shear flow.
The first model. The dispersion curves consist of two families $\mu_{n1} (\nu)$, $\mu_{n2} (\nu)$. First, we consider the family of dispersion curves $\mu_{n1} (\nu)$. All curves in this family lie in the interval $(\mu_{c},\mu_{d})$ which is divided into two intervals by the turning point $\mu_{b}$. Figure 2 shows that both functions in Eq. (12) oscillate in the interval $(\mu_{b}, \mu_{d})$. We replace each of them by asymptotics (10) and obtain
\begin{equation} \tag*{(13)} \beta (\Theta (r(-\pi )) - \Theta (r(0))) = \pi n, \; n=1,2,... \end{equation}This implies that
\begin{eqnarray*} \nu_{n1} (\mu ) =\pm \left| \mu \right|((\pi nb)^{2} (\Theta (r(-\pi)) - \end{eqnarray*} \begin{equation} \tag*{(14)} \Theta (r(0)))^{-2} -1)^{1/2} . \end{equation}The dependence $\mu_{n1} (\nu)$ can be derived from expressions (13), (14) by standard computational algorithms. Figure 2 shows that, in the interval $(\mu_{c}, \mu_{b})$, the second function in (12) oscillates and the first function does not oscillate. Then replacing the second function in (12) by asymptotics (11) and the first function by the asymptotics (10) we can obtain
\begin{eqnarray*} \left|\beta \right|(\Theta (r(-\pi ))) -\pi /4 \,+ 0.5 \arctan \times \end{eqnarray*} \begin{equation} \tag*{(15)} (\exp (-2 \left|\beta \right| \Phi (r(0)))) = \pi n, \; n=1,2,... \end{equation}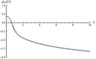 |
| Figure 3 |
In contrast to (12), Eq. (15) can easily be solved numerically, because the left-hand side of this relation (asymptotic approximation of the phase) is a strictly monotonous function. Figure 3 presents the dispersion curve $\mu_{11} (\nu )$ calculated numerically (solid line), its approximation calculated from formula (14) (dotted line), and a numerical solution of Eq. (15) (dashed line). We consider the family of dispersion curves $\mu_{n2} (\nu)$. All dispersion curves of this family belong to the interval $(\mu_{a}, \mu_{e})$. Figure 2 shows that the second function in (12) oscillates, and the first function does not oscillate, and the contribution of the first function to the phase is zero in this case, because the turning point $\mu_{f}$ lies outside the interval $(\mu_{a}, \mu_{e})$. As a result, we obtain
\begin{equation} \tag*{(16)} \left|\beta \right|\Theta (r(-\pi )) - \pi /4 = \pi n, \; n=1,2,... \end{equation}The solution of (16) has the form
\begin{eqnarray*} \nu_{n2} (\mu ) = \pm \left|\mu \right|(((\pi n - \pi/4) b)^{2} \times \end{eqnarray*} \begin{equation} \tag*{(17)} (\Theta (r(-\pi)))^{-2} - 1)^{1/2} . \end{equation}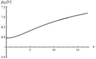 |
| Figure 4 |
We can also obtain the dependence $\mu_{n2} (\nu)$ from expressions (16), (17) by standard computations algorithms. Figure 4 presents the dispersion curve $\mu_{21} (\nu )$ calculated numerically (solid line) and its approximation calculated by formula (17) (dotted line).
In this case, there is only one family of dispersion curves, namely, $\mu_{n} (\nu)$. All other curves of this family lie in $(-\infty ,\mu_{d})$, which is divided by the turning point $\mu_{b}$ into two intervals. In the interval $(\mu_{b}, \mu_{d})$, the solution of dispersion equation (12) has the form (15), where $r(-\pi) = \omega$. In the interval $(-\infty ,\mu_{b})$, dispersion equation (12) has a form similar to (15), where $r(-\pi ) = \omega$. For large values of $\nu$, we have the asymptotics \begin{eqnarray*} \mu_{n} (\mu) = -B_{n} \nu, \; B_{n} = (((\pi n - \pi /4) b)^{2} \times \end{eqnarray*} \begin{equation} \tag*{(18)} (\Theta (r( - \pi )))^{-2} -1)^{1/2} . \end{equation} |
| Figure 5 |
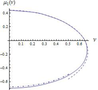
Figure 5 shows the dispersion curve $\mu_{1} (\mu)$ calculated numerically (solid line), its approximation by formula (14) (dotted line), and a numerical solution of Eq. (15) (dashed line).
The third model. In this case, there is one family of closed curves which we denote by $\mu_{n} (\mu)$ (each curve consists of two branches, $\mu_{n}^{+} (\mu)$ is the upper branch, $\mu_{n}^{-} (\mu)$ is the lower branch). All curves of this family lie in the interval $(\mu_{a}, \mu_{d})$. In this interval, there exists only one turning point $\mu_{b}$. In the interval $(\mu_{b},\mu_{d})$, the solution of the dispersion equation has the form (14), and in the interval $(\mu_{a}, \mu_{b})$, the solution of the dispersion equation is obtained by solving Eq. (15) numerically.
 |
| Figure 6 |
Figure 6 shows the dispersion curve $\mu_{1} (\mu)$ calculated numerically (solid line), its approximation by formula (14) (dashed line), and a numerical solution of Eq. (15) (dash-dotted line).
To study the induced IGW in the stratified ocean with shear flows, it is required to solve problem (1)–(2) with a nonzero right-hand side $Q (t,x,y,z,z_{0})$ whose specific form is determined by the form of the perturbation source. If a vertically directed force is considered as the source, then we have
\begin{eqnarray*} Q(t,x,y,z,z_{0}) = \end{eqnarray*} \begin{eqnarray*} \delta'(t) \delta (z-z_{0})(\delta"(x) \delta (y) + \delta"(y) \delta(x)). \end{eqnarray*}In the case of point mass source, we have $Q(t,x,y$, $z,z_{0}) = \delta"(t) \delta (x) \delta (y) \delta'(z-z_{0})$. If this function has the form
\begin{eqnarray*} Q(t,x,y,z,z_{0}) = \delta (x) \delta (y) \delta (z-z_{0})\exp (i\omega t), \end{eqnarray*}then we consider the Green function of problem (3) for an oscillating point source of perturbations located at depth $z_{0}$. Obviously, since the problem under study is linear, using the obtained asymptotic solutions for the Green function, we further can obtain representations for the IGW fields generated by arbitrary nonlocal and nonstationary sources in the stratified ocean with shear flows [Bulatov and Vladimirov, 2012; Svirkunov and Kalashnik, 2014]. One of the main sources of IGW generation in the ocean can be moving atmospheric cyclones. The wave fields generated by this generation mechanism play a significant role in various mechanisms of energy transfer in the depth of the ocean. The experimental detection of IGW trace from a moving hurricane was one of the most impressive achievements in oceanology [Furuichi et al., 2008; Voelker et al., 2019]. At large distances, the real perturbation sources (hurricane, perturbations of atmospheric pressure, cyclone) allow a physically justified approximation by a system of point localized sources taken with certain weights. As a point non-stationary source of IGW generation in the real ocean, one can also consider a steep slope of a transverse ridge in straits, where shear flows and periodic tidal flows take place [Frey et al., 2017; Morozov, 2003, 2008, 2018]. Such an approach is physically justified and permits solving many problems of modeling of linear IGW generation in the ocean with regard to shear flows [Velarde et al., 2018]. At large distances from the perturbation sources, the exact form of the source does not practically influence the wave characteristics of IGW, which are determined by parameters of the stratified medium and the corresponding dispersion laws [Bulatov and Vladimirov, 2019; Bulatov et al., 2019; Svirkunov and Kalashnik, 2014]. In the general case, the solution is a sum of vertical wave modes: $W = \sum_{n} W_{n}$, where each mode is a superposition of plane waves of the form
\begin{eqnarray*} W_{n} = \int_{-\infty }^{\infty} F_{n} (z,\nu ) \times \end{eqnarray*} \begin{equation} \tag*{(19)} \exp (-i(\mu_{n} (\nu )x +\nu y -\omega t)) d\nu , \end{equation}where the eigenfunctions of spectral problem (3) are contained in the amplitude $F_{n} (z,\nu)$ which is a slowly varying function of variable $\nu$. The integral of the form (19) can be calculated at large distances from IGW perturbation sources by the method of stationary phase [Bulatov and Vladimirov, 2012, 2019; Bulatov et al., 2019].
We introduce the following notation for the phase: $\Omega = \mu_{n} (\nu) + \nu y -\omega t$. In the third model, it is required separately to consider the upper $\mu_{n}^{+} (\mu)$ and lower $\mu_{n}^{-} (\mu)$ branches of the corresponding dispersion curve. We use the stationary phase condition $(\partial \Omega/ \partial \nu ) = 0$ to obtain the family of lines of constant phase with parameter $\nu$:
\begin{eqnarray*} x= \frac{\Omega + \omega t}{\mu_{n} (\nu ) -\nu d_{n} (\nu)} , \end{eqnarray*} \begin{equation} \tag*{(20)} y= \frac{d_{n} (\nu )(\Omega + \omega t)}{\mu_{n} (\nu )-\nu d_{n} (\nu )}, \end{equation} \begin{eqnarray*} \mathop{d}\nolimits_{n} (\nu )=\frac{d\mathop{\mu }\nolimits_{n} (\nu )}{d\nu } . \end{eqnarray*}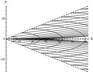 |
| Figure 7 |
 |
| Figure 10 |
 |
| Figure 9 |
 |
| Figure 8 |
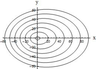
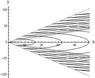
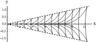
Figure 7–Figure 8 present the results of calculations for the first model, Figure 7 shows the lines of equal phase for $\mu_{11} (\nu)$, and Figure 8 shows the lines of equal phase for $\mu_{12} (\nu)$. Figure 9 presents the lines of equal phase for $\mu_{1} (\nu)$ (second model). Figure 10 shows the lines of equal phase for $\mu_{1} (\nu)$ (third model). For this model, expressions (20) describe the wave pattern of the generated IGW field at $x > 0$. At $ x <0$, a similar family of lines of constant phase is described by relations (20), where it is necessary to use $\mu_{n}^{-} (\nu)$ instead of $\mu_{n}^{+} (\nu)$ in the equation for the phase $\Omega$. The results show that the phase structure of the generated IGW fields significantly depends on the relation between the amplitudes of the bottom and near-surface shear flows.
It should be noted that, for a constant (independent of the depth) shear flow, the wave pattern of the generated IGW fields depends on frequency $\omega$, and, for example, annular waves can exist only at small amplitudes [Bulatov and Vladimirov, 2018]. For linear shear flows, the wave pattern of IGW is determined by the flow properties. In particular, the unidirectional flow generates both wedge-shaped (longitudinal) and annular (transverse) waves (Figure 7–Figure 9), and the multidirectional flow generates only annular (transverse) waves (Figure 10).
The wave pattern of a separate wave mode of the generated IGW fields in the first and second models is a system of wedge-shaped (longitudinal) and annular (transverse) waves (Figure 7–Figure 9). The annular (transverse) waves occupy the whole spatial domain inside the wedge with half-opening angle $\alpha$, and the length of the transverse wave of mode $n$ for $y = 0$ is equal to $2 \pi /\mu_{n} (0)$. The wedge-shaped (longitudinal) waves of each mode are bounded by both the wave front with the half-opening angle $\alpha$ and the wave front (whose position is determined by the asymptotics (18) describing the behavior of $\mu_{n} (\nu)$ for large $\nu$) with the half-opening angle $\beta = \arctan B_{n} < \alpha$. Since there are two distinct families of dispersion curves in the first model, there also exists a wave system of only wedge-shaped (longitudinal) waves (Figure 8).
In the third model, if the amplitude of the bottom and near-surface flows are equal to each other, then the corresponding phase pattern of the wave field is symmetric. If the amplitudes of the bottom and near-surface flows are distinct, then the phase pattern of the generated IGW fields becomes asymmetric. Therefore, the asymmetry of phase patterns of wave fields is one of the signs of noticeable reconstruction in the distribution of shear ocean flows in the water column.
Thus, we have solved the problem of IGW field in a stratified medium of finite depth with multidirectional shear flows. To solve the problem analytically, we used a constant distribution of the buoyancy frequency and three different linear dependences of the shear flown on depth. Using the model hydrology, we obtained analytic expressions describing the dispersion dependences which can be expressed in terms of the modified Bessel function with imaginary index. If the Miles stability condition is satisfied and the Richardson numbers are large, the Debye asymptotics of the modified Bessel function with imaginary index were used to construct analytical solutions. The properties of the dispersion equation are studied and the main analytical properties of the dispersion curves are investigated for different models of the shear velocity distribution. The dispersion curves for the first model are two families of open curves, and each dispersion curve is bounded. The dispersion curves for the second model consist of only one family, and each curve is enclosed in the corresponding semi-infinite interval. The dispersion curves corresponding to the third model consist of one family of closed curves. The phase patterns of the generated IGW fields are numerically calculated for different models of wave generation. The results show that there is a significant dependence of the phase structure of the generated IGW fields on the relation between the bottom and near-surface amplitudes for different models of shear flows.
Bulatov, V. V., Yu. V. Vladimirov (2012) , Wave Dynamics of Stratified Mediums, 584 pp., Nauka, Moscow.
Bulatov, V. V., Yu. V. Vladimirov (2018) , Far fields of internal gravity waves from a nonstationary source, Oceanology, 58, no. 6, p. 796–801, https://doi.org/10.1134/S0001437018060036.
Bulatov, V. V., Yu. V. Vladimirov (2019) , A General Approach to Ocean Wave Dynamics Research: Modelling, Asymptotics, Measurements, 587 pp., Onto Print Publishers, Moscow.
Bulatov, V. V., Yu. V. Vladimirov, I. Yu. Vladimirov (2019) , Far fields of internal gravity waves from a source moving in the ocean with an arbitrary buoyancy frequency distribution, Russian J. Earth Sciences, 19, p. ES5003, https://doi.org/10.2205/2019ES000667.
Fabrikant, A. L., Yu. A. Stepanyants (1998) , Propagation of Waves in Shear Flows, 304 pp., World Scientific Publishing, London, https://doi.org/10.1142/2557.
Fraternale, F., L. Domenicale, G. Staffilan, et al. (2018) , Internal waves in sheared flows: lower bound of the vorticity growth and propagation discontinuities in the parameter space, Phys. Review, 97, no. 6, p. 063102, https://doi.org/10.1103/PhysRevE.97.063102.
Frey, D. I., A. N. Novigatsky, M. D. Kravchishina, et al. (2017) , Water structure and currents in the Bear Island Trough in July–August 2017, Russian J. Earth Sciences, 17, p. ES3003, https://doi.org/10.2205/2017ES000602.
Furuichi, N., T. Hibiya, Y. Niwa (2008) , Model predicted distribution of wind-induced internal wave energy in the world's oceans, J. Geophys. Research: Oceans, 113, p. C09034, https://doi.org/10.1029/2008JC004768.
Gavrileva, A. A., Yu. G. Gubarev, M. P. Lebedev (2019) , The Miles theorem and the first boundary value problem for the Taylor–Goldstein equation, J. Applied and Industrial Mathematics, 13, no. 3, p. 460–471, https://doi.org/10.1134/S1990478919030074.
Massel, S. R. (2015) , Internal Gravity Waves in the Shallow Seas, 163 pp., Springer, Berlin, https://doi.org/10.1007/978-3-319-18908-6_7.
Mei, C. C., M. Stiassnie, D. K.-P. Yue (2017) , Theory and Applications of Ocean Surface Waves. Advanced series of ocean engineering, V. 42, 1500 pp., World Scientific Publishing, London, https://doi.org/10.1142/10212.
Miles, J. W. (1961) , On the stability of heterogeneous shear flow, J. Fluid Mechanics, 10, no. 4, p. 495–509, https://doi.org/10.1017/S0022112061000305.
Miropolsky, Y. Z. (2001) , Dynamics of Internal Gravity Waves in the Ocean, Shishkina O. (ed.), 406 pp., Springer, Berlin, https://doi.org/10.1007/978-94-017-1325-2.
Morozov, E. G. (2018) , Oceanic Internal Tides. Observations, Analysis and Modeling: A Global View, 366 pp., Springer, Dordrecht, https://doi.org/10.1007/978-3-319-73159-9.
Morozov, E. G., G. Parrilla-Barrera, M. G. Velarde, et al. (2003) , The Straits of Gibraltar and Kara Gates: A comparison of internal tides, Oceanologica Acta, 26, no. 3, p. 231–241, https://doi.org/10.1016/S0399-1784(03)00023-9.
Morozov, E. G., V. T. Paka, V. V. Bakhanov (2008) , Strong internal tides in the Kara Gates Strait, Geoph. Research Letters, 35, p. L16603, https://doi.org/10.1029/2008GL033804.
Morozov, E. G., I. E. Kozlov, S. A. Shchuka, et al. (2017) , Internal tide in the Kara Gates Strait, Oceanology, 57, p. 8–18, https://doi.org/10.1134/S0001437017010106.
Pedlosky, J. (2010) , Waves in the Ocean and Atmosphere: Introduction to Wave Dynamics, 260 pp., Springer, Berlin.
Svirkunov, P. N., M. V. Kalashnik (2014) , Phase patterns of dispersive waves from moving localized sources, Phys.-Usp., 57, no. 1, p. 80–91, https://doi.org/10.3367/UFNe.0184.201401d.0089.
Sutherland, B. R. (2010) , Internal Gravity Waves, 394 pp., Cambridge University Press, Cambridge, https://doi.org/10.1017/CBO9780511780318.
Velarde, M. G., R. Yu. Tarakanov, A. V. Marchenko (2018) , The Ocean in Motion, 625 pp., Springer Oceanography, Springer International Publishing AG, Berlin, https://doi.org/10.1007/978-3-319-71934-4.
Voelker, G. S., P. G. Myers, et al. (2019) , Generation of oceanic internal gravity waves by a cyclonic surface stress disturbance, Dyn. Atmosphere Oceans, 86, p. 116–133, https://doi.org/10.1016/j.dynatmoce.2019.03.005.
Watson, G. N. (1995) , A Treatise on the Theory of Bessel Functions, 804 pp., Cambridge University Press, Cambridge.
Received 8 June 2020; accepted 12 June 2020; published June 2020.


Citation: Bulatov V. V., Yu. V. Vladimirov (2020), Dynamics of internal gravity waves in the ocean with shear flows, Russ. J. Earth Sci., 20, ES4004, doi:10.2205/2020ES000732.
Copyright 2020 by the Geophysical Center RAS.