
RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 15, ES3001, doi:10.2205/2015ES000552, 2015
V. P. Trubitsyn1,2, M. N. Evseev1, A. P. Trubitsyn1
1Institute of Physics of the Earth, Russian Academy of Sciences, Moscow, Russia
2Also at Institute of Earthquake Prediction Theory and Mathematical Geophysics, Russian Academy of Sciences, Moscow, Russia
.The regularities of the global intraplate volcanism of the Earth are explained by the mantle plumes originating at the heads and margins of two piles of dense material of the hot and relatively heavy $D"$ layer at the base of the mantle. Due to thermal blanket effect under a supercontinent the overheated region with ascending flows arises in the mantle. These flows distort the $D"$ layer and produce the thermochemical piles in the lowermost mantle under the supercontinent. It is supposed that the pile under Africa originated at the time of existence of Pangea, while the pile under the Pacific Ocean originated at the time of existence of Rodinia. As Africa succeeds to Pangea, the pile under Africa exists until now. But it stays unclear why the pile under the Pacific Ocean exists up to now despite supercontinent Rodinia has been broken-up a long time ago. The numerical models of thermochemical convection in the whole mantle with spherical geometry which include the heavy $D"$ layer allow to clear up effects of supercontinents and lithospheric plates on deformations of the $D"$ layer by mantle flows and formation of the thermochemical piles.
The Earth's volcanoes can be divided on two kinds. The volcanoes of the subduction zones and rifts arise at plate boundaries in the upper mantle and move together with oceanic plates and continents. The volcanoes which show themselves in hot spots and large igneous provinces are caused by mantle plumes originating in the lowermost mantle irrespective of any plate boundaries [Grachev, 2000; Schubert et al., 2001; Trubitsyn, Evseev, 2014].
 |
| Figure 1 |
A mantle plume is an ascending flow of narrow column of hot rocks which takes the mushroom form and become pulsating at high vigor of convection. When the plume reaches the lithosphere its head can break through it. After the processes of partial melting, differentiation and solidification a large igneous province (LIP) can appear. Later the material of the plume tail can break through the lithosphere in batches and a volcanic chain can form. A hot spot is a location of present-day outbreak of a plume tail in a form of an active volcano. The plume outbreak through a moving plate is sketched out in Figure 1.
The hot spots locate largely around Africa and the southern part of the Pacific Ocean. Large igneous provinces (traps on continents and basaltic plateaus on the oceanic floor) represent the magmas erupted in the past, which moved after their formation together with lithospheric plates and are distributed now chaotically on the Earth's surface. However if with the help of paleomagnetic reconstructions one transposes LIPs to the points where they once appeared, then LIPs (as are hot spots) fall roughly into two circles around Africa and the southern part of the Pacific Ocean [Burke, Torsvik, 2004; Torsvik et al., 2010]. Thus over a period of more than 0.5 billion years the majority of the Earth's deep eruptions steadily happened essentially in these regions.
The seismic tomography models show two anomalous zones in the lowermost mantle under Africa and the southern part of the Pacific Ocean which are up to 400 km high [Julian et al., 2014]. In these zones the shear wave velocities are reduced by about 2% so they are called LLSVPs (large low shear velocity provinces) [Bull et al., 2009]. Since shear wave velocities $V_s$ are sensible to temperature and decrease as temperature increases, these zones should be hot. Earlier it was supposed a long time that two giant thermal superplumes rise from the base of the mantle under Africa and the Pacific Ocean.
However it turned out that LLSVPs can hardly be seen in compressional p-waves. At the same time the bulk sound velocities $V_b = (V_s^2 -4 V_p^2/3)^{1/2} =(K/\rho)^{1/2}$ in the LLSVPs are increased [Masters et al., 2000]. In contrast to shear waves, bulk sound velocities are more sensible to composition and increase with elastic modulus and partly with density of material. Hence it follows that LLSVPs correspond to thermochemical piles of hot and heavy material. These zones formed by a chemically distinct component with a high bulk modulus (high-K) are also called high-K structures. According to [Deschamps et al., 2012] observed anomalies of shear wave velocities and bulk sound velocities can correlate with material enriched by 30% in iron and by 20% in (MgFe)-perovscite.
All these observation data could be reconciled assuming that the heavy $D"$ layer is divided by mantle flows into two parts, and that mantle plumes responsible for major eruptions originate at the margins of these giant structures referred to as plume generation zones (PGZ).
 |
| Figure 2 |
Based on the whole set of present-day data of seismology, geochemistry, geology, laboratory data on material properties and numerical modeling it is possible to propose the following hypothetical picture of mantle structure and dynamics. On the Earth's surface from left to right along 20° S latitude there are the Atlantic Ocean with the mid-Atlantic Ridge, Africa, the Indian Ocean with the Indian Ridge, Australia, the Pacific Ocean with the East Pacific Rise, and South America. Figure 2 schematically represents the Earth's sectional view along the same latitude. Clockwise are pictured the above-listed surface features and deep mantle structure under them. Two red-colored regions at the base of the mantle represent high density piles (LLSVPs). Plumes generated at PGZ are also shown in red. Arrows show mantle flow fluid velocities.
The similar hypothetical picture of mantle structure and Earth's dynamics earlier was presented by [Tronnes, 2010] along the equator. However the latitude 20° S crosses the middle parts of LLSVPs.
Convection in heated viscous mantle has four distinctive features. The rigid cold Earth's surface is divided on a system of lithospheric plates. Oceanic plates take part in convective circulation of mantle material sinking into the mantle in subduction zones. Different in chemical and mineral composition lightweight continents float on the mantle. Due to high vigor of convection its ascending flows take the form of pulsating plumes. At the base of the mantle there is the $D"$ layer which consists of heavy material enriched in iron.
Progress of mathematical modeling makes it possible to perform numerical simulations which reproduce all the above-mentioned features of mantle convection and study conditions of their emergence.
Simulations of thermochemical convection are conducted in terms of numerical solution of the governing equations of mass, momentum, and energy conservation for a multicomponent fluid with viscosity defined as a function of temperature, pressure, strain rate, and composition (concentration) $\eta = \eta (T, p, \dot{e}, C)$. Under the extended Boussinesq approximation (EBA), as distinct from the simple Boussinesq approximation (BA), compressibility of a material is considered not only in case of thermal expansion in the buoyancy term of the Stokes equation but also in the energy conservation equation. The latter leads to taking into account adiabatic heating and cooling of descending and ascending mantle flows, respectively. So the convection equations in EBA formulation include, in contrast to BA, total real temperature, which governs viscosity, rather than nonadiabatic temperature.
The governing equations of thermochemical convection for a primary fluid admixed with a different chemical component include the above-mentioned equations plus the equation for the concentration. In nondimensional form these equations [Schubert et al., 2001] are:
\begin{equation} \tag*{(1)}\label{1} - \frac{\partial p}{\partial x_i} + \frac{\partial \tau_{ij}}{\partial x_j} + \left( RaT - \mathop{\Sigma}_{k} R b_k \Gamma_k + RcC \right) \delta_{i3} =0 \end{equation}\begin{equation} \tag*{(2)}\label{2} \frac{\partial T}{\partial t} + U_i \frac{\partial T}{\partial x_i} + Di (T+T_s)U_z = \frac{\partial}{\partial x_i} \left( k \frac{\partial T}{\partial x_i} \right) + \frac{Di}{Ra} \tau_{ij} \frac{\partial U_i}{\partial x_j} +\rho_s H \end{equation}
\begin{equation} \tag*{(3)}\label{3} \frac{\partial U_j}{\partial x_j} = 0 \end{equation}
\begin{equation} \tag*{(4)}\label{4} \frac{\partial C}{\partial t} + U_i \frac{\partial C}{\partial x_i} =0 \end{equation}
where
\begin{eqnarray*} \tau_{ij} = \eta \dot e_{ij}, \qquad \dot e_{ij} = \frac{\partial U_i}{\partial x_j} + \frac{\partial U_j}{\partial x_i} \end{eqnarray*}$U_i$ is the velocity vector; $p$ is dynamic pressure; $T$ is temperature; $T_s$ is surface temperature; $\dot{e}_{ij}$ is strain rate tensor; $H$ is internal heating; $Ra = (\rho_0 g \Delta TD^3/(k_0\eta_0)$ is the thermal Rayleigh number; $Rb_k = \delta \rho_k D^3g/(k_0\eta_0)$ are the phase-change Rayleigh numbers, $Rc= \delta \rho_c D^3g/(k_0 \eta_0)$, are the chemical Rayleigh numbers; $\delta \rho_k$ – is the density jump across a phase change; $\rho_c$ is the density of the different chemical component, $\delta \rho_c= \rho_c - \rho_0$, $Di = Dg\alpha_0/c_p$ is dissipation number; $\Gamma_l$ is the phase function:
\begin{eqnarray*} \Gamma_l = \frac{1}{2} \left( 1+ th \frac{z- z_l(T)}{w_l}\right) \end{eqnarray*}
where $z_l$ is the depth of a phase change, and $w_l$ is the width of a phase transition. The dependence of depth of a phase change on temperature is defined as
\begin{eqnarray*} z_l(T) = z_l^0 + \gamma_l (T - T_l^0) \end{eqnarray*}
where $\gamma_l$ is the Clapeyron slope, $z_l^0$ and $T_l^0$ – the average depth and temperature of a phase change [Tosi, Yuen, 2011].
For solving the equations (1)–(4) we take the simple boundary conditions with impermeable, shear stress free, and isothermal boundaries. The temperatures on the upper and lower boundary are taken equal to $T_s = 300$ K and $T = T_s + \Delta T$, respectively. The initial conditions correspond to a conductive heating of the layer with an arbitrary small perturbation of temperature.
For the non-dimensional form we use the following scaling factors: the mantle thickness $D$ for distance; the temperature difference across the whole mantle $\Delta T$ for temperature; the characteristic values of mean density $\rho_0$, viscosity $\eta_0$ and heat capacity $c_p$; the characteristic values of thermal expansivity $\alpha_0$ and thermal conductivity $k_0$; as well as the values $\kappa = k_0/(\rho_0c_p)$ for thermal diffusivity, $t_0 = D^2/\kappa$ for time, $U_0 = \kappa/D$ for velocity, $q_0 = k_0 \Delta T/D$ for heat flux, $\sigma_0 = \eta_0 \kappa/D^2$ for dynamic pressure and stress, and $H_0 = c_p \kappa \Delta T/D^2$ for the internal heat generation.
The parameter values for the mantle were taken from [Tosi, Yuen, 2011] and are the following: $D = 2890$ km, $\rho_0 = 4.5 \times 10^3$ kg m$^{-3}$, $c_p = 1.25 \times 10^3$ J kg$^{-1}$ K$^{-1}$, $\eta_0 = 3 \times 10^{22}$ Pa s, $\kappa_0 = 0.59 \times 10^{-6}$ m$^2$ s$^{-1}$, $\alpha_0 = 3.0 \times 10^{-5}$ K$^{-1}$, $\Delta T = 3500$ K, $H = 5.6 \times 10^{-12}$ W kg$^{-1}$. At this values the scaling factors for heat flux and internal heat generation are $q_0 = 4$ mW m$^{-2}$ and $H_0 = 3.1 \times 10^{-13}$ W kg$^{-1}$. So the Rayleigh number, the dissipation number, and the dimensionless internal heat generation are $Ra = 1.9 \times 10^7$, $D_i = 0.68$, and $H = 20$, respectively. Density jumps $\delta\rho$ and phase slopes $\gamma$ were taken equal $\Delta \rho_{410} = 0.06\rho$, $\gamma_{410} = 3$ MPa K, $\Delta \rho_{660} = 0.076\rho$, $\gamma_{660} = -3$ MPa/K, $\Delta \rho_{2700} = 0.015\rho$, $\gamma_{2700} = 13$ MPa/K.
For the numerical solving the convection equations (1)–(4) we use the finite element code CitcomCU originally developed by [Moresi, Gurnis, 1996]
and further elaborated by [Zhong, 2006]. A version of the code for 2D Cartesian geometry was supplemented with the more accessible output files and automated graphics [Evseev, 2008].
A version of the code for spherical geometry was extended in a similar manner by M. Evseev [Trubitsyn, Evseev, 2014].
We calculated simple models of mantle convection in 2-D approximation of 3-D spherical geometry using a spherical annulus domain [Ismail-Zadeh, Tackley, 2010], namely a 2-D slice along the equator. We used a step viscosity function which has a viscosity jump between the upper and lower mantle, varying Rayleigh numbers and taking into account phase transitions. The state of fully developed convection with a fixed highly viscous continent was taken as an initial state. Then we inserted at the base of the mantle the layer of high-density material with thickness 200 km (in order to model $D"$) and computed the subsequent time evolution of convection structure.
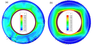 |
| Figure 3 |
Figure 3 shows the results for moderate vigor of convection with viscosities of the upper and lower mantle $10^{22}$ Pa s and $10^{24}$ Pa s, respectively, that corresponds to the average Rayleigh number about $1.1 \times 10^4$. The density contrast between $D"$ and the overlying mantle was equal to 10%. The dimensionless temperature distribution is shown in color. The flow velocities are shown by arrows. The viscosity jumps at the base of the highly viscous continent and at the boundary between the upper and lower mantle are depicted by white lines.
As seen from Figure 3, when the density contrast is equal to 10% the $D"$ layer is strongly distorted and divided into two piles under the supercontinent and at the opposite side. By comparing Figure 2 and Figure 3 it can be seen that even a very simple convection model with a supercontinent can offer a fundamental explanation for the emergence of two piles of the heavy material at the base of the mantle.
It is important that at low vigor of convection its structure becomes quadrupole (two ascending and two descending mantle flows). As seen from Figure 3b, the mantle warms up under the supercontinent acting as a thermal blanket, and there arises a global ascending flow. Obviously, this flow carries away the material of $D"$ from the base of the mantle and builds up the pile of this heavy material under the supercontinent. The ascending flows are most pronounced at the pile margins and rise to the surface at the supercontinent margins. Then these flows diverge sideward, cool down and sink into the mantle. Upon reaching the lowermost mantle the flows displace the material of $D"$ both under the supercontinent and to the opposite side. Thereby the second pile is created. Thus at low vigor of convection the quadrupole structure is established only due to presence of a supercontinent, and the $D"$ layer transforms to two piles of heavy material.
However this model with the small Rayleigh number (too high viscosity of the lower mantle) requires an unlikely high density contrast between $D"$ and the overlying mantle to prevent mixing of $D"$ material. The point is that high mantle viscosity leads to more strong distortions of thermochemical piles.
To evaluate the influence of convective vigor on the convection structure, evolution and distortion of the $D"$ layer, the models with higher Rayleigh numbers have been calculated.
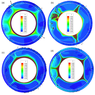 |
| Figure 4 |
Figure 4 illustrates the results at a Rayleigh number $Ra=1.1 \times 10^6$ with density contrasts between $D"$ and the overlying mantle 4%, 20%, and 7%. Figure 4a shows the initial position of the spherical $D"$ layer at the time of its placing into the mantle with established convection in the presence of the supercontinent, which is situated on the left and shown by a white line. Another white line shows the boundary between the upper and lower mantle at a depth of 660 km. Figure 4b gives the calculated structure of established mantle convection at a $D"$ boundary density contrast of 4%. In the case of relatively small $D"$ density the layer strongly deforms and is partly mixed. Figure 4c shows the convective structure at a density contrast of 20%. Under such high density contrast mantle flows almost do not deform the layer $D"$. As seen from Figure 4d at a density contrast of 7% the shape of the $D"$ layer becomes very uneven. In this case the $D"$ layer has a small effect on the convective structure which again looks like that of Figure 4a.
As can be seen of comparing Figure 3b and Figure 4d, the deformation of the $D"$ layer shows some tendency toward spatial separation with grouping of bulges under a supercontinent, as in the case of low convective vigor (under viscosity of the lower mantle more than $10^{24}$ Pa s). However Figures 4b, 4c and 4d show that under viscosity less than $10^{22}$ Pa s the convective vigor is already sufficiently high and the role of a supercontinent goes down. As a result a pronounced pile does not arise on the side opposite to a supercontinent.
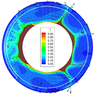 |
| Figure 5 |
At the same time convective structure of the real mantle is strongly influenced by Pacific Plate [Trubitsyn, Trubitsyn, 2014]. As long as the construction of self-consistent spherical convection models with plate generation is still at the development stage, the present paper considers Pacific Plate only kinematically, namely in the boundary conditions which prescribe a fixed surface velocity on the limited area between a ridge and subduction zone. Let us assume that the mid-ocean ridge locates opposite to the supercontinent in the range of longitudes $-5\mbox{°} < \theta < 5\mbox{°}$. In the model of Figure 5 the surface velocity was taken to be $V_\theta = 2$ cm yr$^{-1}$ when $5\mbox{°} < \theta < 100\mbox{°}$, and $V_\theta = -2$ cm yr$^{-1}$ when $160\mbox{°} < \theta < 355\mbox{°}$.
As seen from Figure 5, taking into consideration both a supercontinent and the Pacific Plate leads to the convective flows which separate the $D"$ layer into two thermochemical piles. In this case mantle plumes concentrate both under a supercontinent and the Pacific Ocean.
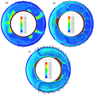 |
| Figure 6 |
Figure 6 illustrates the calculation results for even more vigorous convection at ten-fold density contrast between the upper and lower mantle and a Rayleigh number of $1.1\times 10^7$ corresponding to the upper mantle viscosity $10^{20}$ Pa s and the lower mantle viscosity $10^{21}$ Pa s. In the model of Figure 6b the plate velocity is $V_f = 6$ cm yr$^{-1}$ while in the model of Figure 6c it takes of 12 cm yr$^{-1}$. In the latter case, at high velocity of the Pacific Plate, the effect on convective structure becomes greater, and two piles under supercontinent and the Pacific Plate are more pronounced.
The presented numerical models show that thermal blanket effect of a supercontinent produces warming of the mantle and reorganization of convection flows. There arises giant thermal anomaly under a supercontinent bearing a resemblance to "anticyclone". Mantle flows deform the heavy $D"$ layer. Its evolution depends on convective vigor and density of heavy material.
At the low vigor of convection in high-viscosity mantle with Rayleigh numbers less than $10^5$ the $D"$ material almost is not deformed at a density contrast more than 30%, and is mixed at a density contrast less than 5%. When the density contrast equals 10% the $D"$ layer separates into two thermochemical piles due to influence of a supercontinent, even without considering a role of Pacific Plate.
At the high vigor of convection with Rayleigh numbers of order $10^7$, the $D"$ material heavier than the overlaying mantle less than 4% can be strongly deformed and separate into several piles. At a density contrast more than 15% the $D"$ layer is only weekly deformed. At a density contrast between 5–7% a pronounced pile is formed under a supercontinent. As the $D"$ layer contacts with the very hot liquid Earth's core and convection within it is suppressed, material of piles heats up strongly. The temperature inside piles is elevated by about 1000 K. Ascending mantle flows in the form of plumes originate mainly at the pile margins in PGZ. After rising they bear against a supercontinent and in large part crop up at the margins of a supercontinent. Later the material of these flows cools down and sinks into the mantle. Upon reaching the lowermost mantle the flows displace the material of $D"$ sideways. At the high vigor of convection without a lithospheric plate, several convective cells and correspondingly several piles can be formed outside a supercontinent.
However the high-viscosity lithosphere of the real Earth is divided on plates and on the side opposite to Africa there is the large Pacific Plate which promotes the formation of a great convective cell. Owing to this fact, even at high vigor of convection the $D"$ layer separates not into several scattered piles but in fact into two piles both under a supercontinent and under the Pacific Ocean. In this case the corresponding density contrast should be a few percents. So the large lithospheric plate along with supercontinent can influence on the $D"$-pile origin.
The present paper considered rather simple models of mantle convection with a step viscosity function, since our goals were to reveal basic possibility for formation of two thermochemical piles and to understand roles of a supercontinent and a large oceanic plate. More accurate rheological models with temperature- and pressure-dependent viscosity taking into account the present-day positions of continents and oceanic plates could get more specific information about the conditions of the $D"$ layer deforming and formation of thermochemical piles.
Bull, A. L., A. K. McNamara, J. Ritsema (2009), Synthetic tomography of plume clusters and thermochemical piles, Earth Planet. Sci. Lett., 278, p. 152–162, doi:10.1016/j.epsl.2008.11.018.
Burke, K., T. H. Torsvik (2004), Derivation of large igneous provinces of the past 200 million years from long-term heterogeneities in the deep mantle, Earth Planet. Sci. Lett., 227, p. 531–538.
Deschamps, F., L. Cobden, P. Tackley (2012), The primitive nature of large low shear wave velocity provinces, Earth Planet. Sci. Lett., 349–350, p. 198–208, doi:10.1016/j.epsl.2012.07.012.
Evseev, A. N. (2008), Mantle convection and phase transitions, The Ninth International Conference on Physicochemical and Rock Physical Studies for Earth Sciences, p. 223–225, IFKh RAN, GEOKhI RAN, Moscow.
Grachev, A. F. (2000), Mantle plumes and problems of geodynamics, Izv. Phys. Earth, 36, no. 4, p. 263–294.
Ismail-Zadeh, A., P. J. Tackley (2010), Computational Methods for Geodynamics, 313 pp., Cambridge Univ. Press, Cambridge, doi:10.1017/CBO9780511780820.
Julian, B. R., G. Foulger, O. Hatfield, S. Jackson, E. Simpson, J. Einbeck, A. Moore (2014), Hotspots in Hindsight, AGU Fall Meeting, San Francisco 1, 15–19 December 2014, p. S51B–4468, AGU, Washington, DC.
Masters, G., G. Laske, H. Bolton, A. M. Dziewonski (2000), The relative behaviour of shear velocity, bulk sound speed, and compressional velocity in the mantle: implications for chemical and thermal structure, Karato S.-I., Forte A. M., Liebermann R. C., Masters G., Stixrude L. (eds.), Earth's Deep Interior: Mineral Physics and Seismic Tomography From the Atomic to the Global Scale, p. 63–87, Am. Geophys. Union, Washington, DC.
Moresi, L. N., M. Gurnis (1996), Constraints on lateral strength of slabs from 3-D dynamic flow models, Earth Planet. Sci. Lett., 138, p. 15–28, doi:10.1016/0012-821X(95)00221-W.
Schubert, G., D. L. Turcotte, P. Olson (2001), Mantle Convection in the Earth and Planets, 940 pp., Cambridge Univ. Press, Cambridge, England, doi:10.1017/CBO9780511612879.
Torsvik, T. H., K. Burke, B. Steinberger, S. Webb, L. Ashwal (2010), Diamonds sampled by plumes from the core-mantle boundary, Nature, 466, p. 352–355, doi:10.1038/nature09216.
Tosi, N., D. Yuen (2011), Bent-shaped plumes and horizontal channel flow beneath the 660 km discontinuity, Earth Planet. Sci. Lett., 312, p. 348–359, doi:10.1016/j.epsl.2011.10.015.
Tronnes, R. G. (2010), Structure, mineralogy and dynamics of the lowermost mantle, Min. Petrol., 99, p. 243–261, doi:10.1007/s00710-009-0068-z.
Trubitsyn, V. P., A. P. Trubitsyn (2014), Numerical model for the generation of the ensemble of lithospheric plates and their penetration through the 660-km boundary, Izvestiya, Physics of the Solid Earth, 50, no. 6, p. 853–864, doi:10.1134/S106935131406010X.
Trubitsyn, V. P., M. N. Evseev (2014), Mantle plumes on the boundary of upper and lower mantle, Doklady Earth Sciences, part 1, 459, p. 1397–1399, doi:10.1134/S1028334X14110099.
Zhong, S. (2006), Constraints on thermochemical convection of the mantle from plume heat flux, plume excess temperature and upper mantle temperature, J. Geophys. Res., 111, p. B04409, doi:10.1029/2005jb003972.
Received 3 August 2015; accepted 3 August 2015; published 28 August 2015.


Citation: Trubitsyn V. P., M. N. Evseev, A. P. Trubitsyn (2015), Influence of continents and lithospheric plates on the shape of
Copyright 2015 by the Geophysical Center RAS.