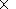 10
6. The thermal diffusivity was assumed the same for
continents and the mantle and amounted to 2
10
6. The thermal diffusivity was assumed the same for
continents and the mantle and amounted to 2
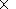 10-6 m2 s-1. The thicknesses of
all the six continents were set equal to 150 km; the thicknesses of all the
ten
islands were set at 100 km.
10-6 m2 s-1. The thicknesses of
all the six continents were set equal to 150 km; the thicknesses of all the
ten
islands were set at 100 km.
V. P. Trubitsyn
Schmidt Institute of Physics of the Earth, Russian Academy of Sciences, Moscow, Russia
Processes of differentiation and convective mixing of Earth's substance, in particular, thermocompositional convection, took place throughout the history of the Earth. However, thermal convection is presently the main driving mechanism of global geodynamic processes in the Earth. In thermal convection, hot and light (due to thermal expansion) material moves from below toward the surface, where it spreads, becomes heavy upon cooling and sinks into the mantle. The resulting circulation pattern involves heat flux maximums above ascending mantle flows and minimums above descending ones. The Earth's average of the heat flux is proportional to the convection velocity magnitude. The observed distribution of the Earth's heat flux and the variation in the oceanic lithosphere thickness as a function of age are consistent with laws of thermal convection.
Thermal convection arises if temperature increases downward with a gradient higher than its adiabatic value. In the Earth, the latter is about 0.4 K km -1, which yields a mantle temperature difference of about 1200 K (e.g. see [Trubitsyn, 2000a]). Ascending material expands and cools due to a decrease in pressure. If the real temperature in the Earth were below the adiabatic distribution curve, the rising material would become colder and heavier as early as it moves toward the surface and could not reach the surface. The temperature of material reaching the surface is characterized by the so-called potential temperature, which is equal to the difference between the real and adiabatic temperatures at a given point, and precisely this temperature excess gives rise to thermal convection in the viscous mantle. In addition to the superadiabatic temperature distribution, the thermal convection onset requires an additional supercritical excess temperature allowing the buoyancy force of material to overcome viscous drag forces. The convection intensity characterized by the dimensionless Rayleigh number is proportional to the superadiabatic temperature excess. Vigorous thermal convection in the Earth's mantle takes place with a Rayleigh number of ~10 7 and a total superadiabatic temperature difference of ~2500 K.
Along with thermal convection, compositional convection with ascending lighter and descending heavier flows can also take place in multicomponent material. However, the related density anomaly is associated with variations in the chemical or mineralogical composition rather than temperature. Chemical differentiation controlled the convection pattern in the earlier period of the Earth's history, when the iron core was growing. Sinking iron entrained and set the whole mantle in motion. However, geochemical data indicate that, on the whole, the growth of the core stopped in the first 60-100 Myr after the Earth's formation [McCulloch and Bennett, 1998]. Presently, convective redistribution of material is going on in the liquid core and, on the regional scale, in the mantle (within shallow magma chambers producing crustal material by melting). Only an insignificant amount of lighter material previously entrained by iron can enter the mantle from the core.
The fact that compositional convection in the present Earth cannot be the main driving force of mantle flows is evident from the following considerations. If the lower density of material involved in mantle upwellings were due to the chemical composition rather than temperature, the mid-oceanic ridge magma would be hot rather than cold. As mentioned above, the thermal convection intensity is directly proportional to the potential temperature, i.e. the temperature excess of erupting magmas compared to the Earth's surface temperature. In the case of chemical convection (in the absence of thermal convection and therefore at zeroth potential temperature) hot material, upon reaching the surface, should cool completely due to decompression.
Furthermore, thermal convection circulation is driven by cooling of hot material during its motion along surface. If the lower density of material that arrived at the surface is due to its chemical composition, how can this material become heavier and sink into the mantle? The mass of presently liberated gases is insufficient to set the whole mantle in motion. It seems unreasonable to state that chemical convection makes a comparable contribution to driving forces of mantle flows only because processes of both chemical and thermal convection take place in the mantle. Although the contribution of chemical differentiation to the driving forces of mantle convection is small, the chemical differentiation is responsible for the global redistribution of isotopes. Being frozen in circulating material of the mantle, isotopes are transported passively in the highly viscous mantle. Their rapid partitioning is possible only in magma chambers (and in the surrounding zone of partial melting).
Due to incomplete mixing of the mantle, its material is chemically homogeneous on large spatial scales and sharply heterogeneous on small scales. Given an average velocity of mantle flows of about 10 cm yr-1, the mantle convection can accomplish no more than 40 whole-mantle overturns. Moreover, the mantle material permanently recirculates. Both the continental crust and continental sediments are entrained by the oceanic crust in subduction zones, thereby producing local sources of chemical heterogeneity. However, density inhomogeneities due to chemical composition can significantly affect the thermal convection structure only in the liquid core and magma chambers. We should note that phase transitions unrelated to the chemical composition redistribution are described by equations of thermal, rather than chemical, convection.
A particularly heterogeneous part of the mantle is the continental lithosphere. Since this lithosphere is permanently moving together with continents, a continent can be regarded in geodynamics as the continental crust together with the underlying lithosphere. Such an interpretation should take into account that the lower boundary of the continental lithosphere can vary during the motion of the continent. This boundary is both a thermal and a chemical discontinuity. When a moving continent remains for a long time on a hot mantle, the underlying lithosphere heats and softens, and the material at its base is partly entrapped by mantle flows. This can account for the small thickness of continental lithosphere under the African continent. Because this continent was relatively immobile in the Phanerozoic and hindered the heat release from the mantle, the underlying mantle heated and ascending mantle flows became more intense. As a result, the continental lithosphere thinned and the whole continent was uplifted.
This paper addresses thermal convection in the mantle with floating continents. Since the buoyancy of continents is due to their distinction in mineralogical and chemical composition from the mantle, mantle convection with floating continents takes into account this fundamental factor, which is a consequence of chemical differentiation of mantle material in magma chambers both beneath mid-oceanic ridges and in the continental lithosphere itself.
Thermal convection in the mantle has several distinctive features that determined the recent geodynamics of the Earth.
(1) Notwithstanding relatively low velocities of mantle flows (1-10 cm yr-1 ), mantle convection is nonstationary and quasi-turbulent. Therefore, along with regular circulation of mantle material, narrow jets, plumes, diapirs and floating-up thermics arise in the mantle.
(2) The endothermic olivine-perovskite phase transition at a depth of 660 km is responsible for partial stratification of the mantle. The effect of this phase transition was stronger in the ancient, hotter mantle, and mixing periods of the upper and lower mantle material were episodic and short. In these periods, large amounts of oceanic and, in part, continental crust were entrained down to the base of the lower mantle. During cooling of the mantle, the barrier effect at the phase boundary weakens and plumes are transformed into regular upwellings of the whole-mantle convection.
(3) Viscosity sharply drops with a rise in temperature and increases with a rise in pressure. Under mantle conditions, it varies by more than ~20 orders, from ~103 Pas in basaltic melts of magma chambers to ~1026 Pas in the cold lithosphere. The temperature distribution that is established during convection is characterized by abrupt rises in temperature in the upper and lower conductive boundary layers. For this reason, a low-viscosity asthenospheric layer arises at depths of 100-200 km beneath oceans and at the mantle base. They vary in thickness because thermal convection produces horizontal temperature variations in the mantle of up to 300 K.
(4) The average temperature of the lithosphere is much lower than the melting point. Therefore, the lithosphere is more brittle than the remaining mantle. Due to stress variations, the lithosphere breaks up into plates moving across the Earth's surface. These rigid plates are capable of thrusting over or under one another at small angles. However, the oceanic lithosphere can strongly deform and sink in subduction zones, because bending stresses acting for long time make the lithospheric substance ductile.
(5) Nearly one-third of the Earth's surface is covered by continents, which hinder the heat efflux from mantle. With an average mantle heat flux of ~70 mW m-2 (without regard for the radioactive heat of continental crust), the heat flux is ~90 mW m-2 in oceans and ~30 mW m-2 in continents. Since continents redistribute the heat flux from the mantle, they affect significantly the entire structure of mantle convection. The mechanical and thermal interaction of mantle with continents is the only factor capable of accounting for such processes as the formation of continental lithosphere, the contemporary state of mantle under continents, the formation and breakup of supercontinents, and the mechanism forming the Earth's face.
The first three properties of mantle convection and their effects in global geodynamics have been studied for the last three decades. In particular, this research has led to the creation of kinematic theory of plate tectonics and theory of mantle convection with phase transitions. Presently, properties of both stratified and whole-mantle convection have been studied. Detailed numerical models of the present Earth are constructed [Schubert et al., 2001] and various hypothetical geochemical models accounting for the origins of observed geochemical reservoirs are proposed [Tackley, 2000].
At present, a complete theory of the oceanic lithosphere is being constructed [Tackley, 2000; Zhong et al., 2000]. Rheological properties of the lithosphere in this theory are included in equations of mantle convection. Therefore, the bending and sinking of the oceanic lithosphere, as well as its breakup into rigid plates, are obtained as a result of the solution of a self-consistent system of equations.
Mantle convection including continents was first studied in the case of immobile continents [Lowman and Jarvis, 1993, 1996; Nakanuki et al., 1997; Trubitsyn and Bobrov, 1994; Trubitsyn and Fradkov, 1985]. However, it was found out that fundamental features of global tectonics are due to precisely the motions of continents and their nonlinear interactions with mantle flows. There are two approaches to the modeling of mantle convection interaction with moving continents. Gurnis [1988] and Gurnis and Zhong [1991] constructed 2-D models that treated continents as highly viscous bodies in the mantle whose motion was actually calculated without markers, i.e. without using explicit equations of motion of continents. One might state that mantle convection with floating continents is considered in this approach as thermocompositional convection.
Fundamentals of the theory of mantle convection with floating solid continents were developed in terms of Cartesian and spherical 3-D models in [Trubitsyn, 2000b; Trubitsyn and Rykov, 1995, 1998a, 1998b, 1999, 2000]. Equations of mantle convection were complemented with Euler equations describing translatory motions and rotations of solid continents interacting with mantle and with each other. The model of floating solid continents is considered in this theory as a first approximation [Trubitsyn, 2000b] and determines the position and velocities of continents, the temperature distribution within the continents, all mantle forces applied to continental surfaces submerged in the mantle, and the forces due to collisions of continents. Since strain values in continents are much smaller than the amplitudes of their movements, the strains and stresses within continents can be calculated at each time step in the iterative process of the next approximation, using an appropriate rheological model and the known external forces. Calculations of mantle convection with floating solid continents showed that continents are not passive structures but can affect significantly the evolution of mantle convection. They may be regarded as frozen in the oceanic lithosphere in only short periods of geological history. The continental lithosphere exists for a few billions of years only because floating continents (together with the continental lithosphere) are regularly drawn toward cold mantle downwellings. Therefore, the continental lithosphere under moving continents is permanently cold, highly viscous and strong. On the other hand, the mantle underlying an immobile continent inevitably heats with time (over about 200-500 Myr) due to the heat screening effect and the resulting hot ascending flows heat the continental lithosphere and the crust and tend to break them up. This effect also accounts for the breakup of supercontinents.
Results of long-term numerical experiment are presented in [Trubitsyn and Rykov, 1998b] for an idealized model with 12 continents floating on a spherical mantle with due regard for their mechanical and thermal interaction with the mantle and between each other. It was shown that such continents can repeatedly converge (to form a supercontinent) and diverge, without invoking any additional complicating processes.
This work presents calculations of a spherical; evolutionary model of mantle convection with floating continent coinciding in shape and size with the present six continents and ten islands. As an initial, we took convection in the contemporary Earth with a 3-D temperature distribution calculated from seismic tomography data.
The mantle is modeled by a viscous spherical shell. The free-slip condition and a fixed temperature T=T0 are set at the lower (core/mantle) boundary. The free-slip condition and the constant temperature T = 0 are also set at the upper boundary parts unoccupied by continents. The continents are modeled by thick solid plates floating, like rafts, in the mantle. The no-slip condition is imposed on submerged lower and lateral surfaces of the continents; i.e. both normal and tangential velocity components are continuous at these surfaces. Temperature and heat flux are also set continuous at the mantle/continent contact surfaces. The thickness of continental parts above the mantle surface is neglected. The temperature is set at zero at any point of the upper surfaces of continents.
The mantle viscosity is assumed to be constant. Phase transitions in the mantle
were ignored. The intensity of mantle convection was characterized by the
Rayleigh number Ra = 3
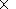 10
6. The thermal diffusivity was assumed the same for
continents and the mantle and amounted to 2
10
6. The thermal diffusivity was assumed the same for
continents and the mantle and amounted to 2
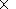 10-6 m2 s-1. The thicknesses of
all the six continents were set equal to 150 km; the thicknesses of all the
ten
islands were set at 100 km.
10-6 m2 s-1. The thicknesses of
all the six continents were set equal to 150 km; the thicknesses of all the
ten
islands were set at 100 km.
Equations of mantle convection and motion of continents are given in Appendix 1.
The contemporary position of six continents (Eurasia, North America, South America, Africa, Australia, and Antarctic) and ten islands (Madagascar, Kalimantan, Greenland, Guinea, Great Britain, Japan, Ireland, Iceland, Sumatra, and New Zealand) was taken as an initial position. Each archipelago mentioned above was modeled as a plate.
The 3-D temperature distribution in the present mantle was taken as an initial distribution of temperature. A laterally averaged temperature distribution with depth in the present mantle is known on a first approximation (e.g. see [Schubert et al., 2001; Solheim and Peltier, 1994; Tackley, 1996; Tackley et al., 1994; Trubitsyn and Rykov, 2000].
Since lateral variations in temperature are on the order of 300 K, they can be considered as corrections to the radial distribution of temperature and can be found under the assumption that lateral density variations in the mantle are proportional to variations in seismic wave velocities [Anderson, 1989]. The conversion coefficient d lnr/d ln Vs is usually found from mineral data of laboratory measurements and theoretical calculations. Kaban and Schwintzer [[2000] determined this coefficient directly from comparison between seismic tomography data and gravity anomalies. The density ( r ) distribution in the oceanic mantle was first found from gravity data. Comparison of this distribution with S wave velocity data yielded the variation of the coefficient d lnr/d ln Vs in the oceanic mantle. This coefficient varies significantly with depth but, because a constant viscosity is taken for calculations of the motion of continents, we took for simplicity an approximate average value of 0.1 for the coefficient d lnr/d ln Vs.
Density variations in the mantle depend on both temperature and chemical-mineralogical
composition. Thermal convection in the mantle mixes its material,
smoothing variations in its composition, but produces lateral variations in
temperature. As mentioned in Introduction, variations in the chemical
composition can only persist on small spatial scales due to incomplete mixing.
Assuming that density variations are mainly due to variations in temperature,
r=r0(1-aT), and setting the expansion coefficient at
a=2 10-5,
we
obtain the value
d ln Vs/dT=-2
10-5,
we
obtain the value
d ln Vs/dT=-2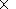 10-4 K
-1 for the conversion coefficient of
seismic tomography data into temperature. The
Vs distribution was taken after
Ekstrom and Dziewonski [1998].
10-4 K
-1 for the conversion coefficient of
seismic tomography data into temperature. The
Vs distribution was taken after
Ekstrom and Dziewonski [1998].
Note that the assumption on chemical heterogeneity of the mantle is unrelated to the continental lithosphere. Since the latter moves along with the crust of a moving continent and its substance is not involved in the convective mixing, substantial chemical heterogeneities should have arisen in the continental lithosphere over a few billions of years. Volatiles could transport iron (and other elements and compounds) from continental lithosphere to crust. According to estimates of [Forte and Perry, 2000], the iron deficit significantly decreases the density of anomalously cold material of the continental lithosphere. The lithosphere density variations due to the iron deficit and temperature are comparable on the order of magnitude. On the other hand, seismic velocities vary weakly with changes if chemical composition. Therefore, in a first approximation, the temperature of continental lithosphere can be calculated with the same conversion coefficient of seismic velocities. The effect of lower density of the continental lithosphere due to a chemical composition is accounted for in the model considered by incorporating this density deficit into the buoyancy of a continent.

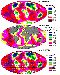
|
| Figure 1 |
This initial temperature distribution and coordinates of continents were used in the equations of convection with floating continents, presented in Appendix 1. The system of equations of convection with floating continents was solved numerically by an iterative finite-difference method [Trubitsyn and Rykov, 1998b, 2000] in spherical coordinates. In this approach, continents were treated as spherical caps floating on a sphere.
Knowing the initial temperature distribution and the position of continents at t=t1=0, the temperature distribution in the mantle and continents at the next time moment t2=t1+dt is found from equations (2) and (14) presented in Appendix 1. This new temperature distribution is substituted in Equation (1) and mantle flow velocities are found. The velocities are used to determine viscous forces acting on the continents and velocities of the continents. The continents are then rotated and moved by a distance corresponding to these velocities and the time interval dt.
The calculation of the evolution of the mantle-continents system yielded results presented in Figures 2-8 and, as an animation, in Appendix 2.
|
| Figure 2 |
The velocities of mantle flows and continents at the same time moment are presented in the lower part of Figure 2 against the background of the temperature distribution at a depth of 200 km. As seen from this figure, the contemporary continents are located in the coldest areas, above mantle downwellings.

|
| Figure 3 |
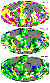
|
| Figure 4 |
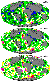
|
| Figure 5 |

|
| Figure 6 |

|
| Figure 7 |
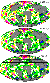
|
| Figure 8 |
Thus, the future evolution of moving continents in this model is controlled by two Pacific systems of subduction, at the eastern and western Pacific margins. Linear systems of mantle upwellings beneath Pacific and Atlantic mid-oceanic ridges are restraining factors pushing continents apart. Antipodes of two major subduction centers of the Pacific Ocean are two giant hot mantle upwellings beneath this ocean and Africa. The preliminary model under consideration indicates that a new hot mantle upwelling will arise beneath Arctic in about 200-300 Myr, whereas the sub-African hot mantle upwelling will shift toward the present-day Red Sea.
We may suppose that the sub-African hot mantle upwelling is a remnant of the mantle flow that arose beneath Pangea 250 Myr ago. The contemporary sub-Pacific hot mantle upwelling is a remnant of the flow that arose beneath Rodinia 1 Gyr ago. Modeling results show that the lifetime of supergiant mantle flows can approximately amount to 1 Gyr. Therefore, the mantle flow presently existing beneath the Pacific, and the flow developed beneath Pangea should was pulled beneath relatively immobile Africa. Another of its branches will possibly be enhanced beneath the Arctic Ocean due to the joint heat-screening effect of Eurasia and North America.
The calculated evolution of continents can be viewed in more detail via the JavaScript-based animation (see Appendix 2).
This work is an apparently first attempt to model the future evolution of the present-day continents and islands floating on a spherical mantle. This model should by no means be regarded as prediction of the drift of continents; it demonstrates only that such modeling is basically possible. The following drawbacks of the model can be noted.
(1) The model neither describes nor takes into account the division of the oceanic lithosphere into plates. Presently, the theory of mantle convection including a complex rheological law for viscosity is at the stage of its development. As has only been shown as yet, the stress dependence of viscosity enables an effective description of both the bending of a rigid plate and its breakup due to ductile flow and fracture. The dynamic theory of plate tectonics will be constructed only after the problem of oceanic lithosphere breakup is solved.
(2) The model presented in this paper uses an underestimated effective Rayleigh number. The Rayleigh number, inversely proportional to viscosity, is a parameter of the equations of convection characterizing the vigorousness of convection. The mantle viscosity being variable, an effective Rayleigh number is used. In calculating the mantle convection structure, it is appropriate to use the mantle viscosity average amounting to about 107 in the case of the Earth. However, continents are not inside the mantle but on its surface and move in the field of oceanic plates. Therefore, in calculating velocities of continents, it is more appropriate to use, rather than the viscosity averaged over the whole mantle, an average mantle viscosity that is taken with a larger weight accounting for a highly viscous region of the mantle. With larger Rayleigh numbers, the motion of continents becomes more chaotic and inconsistent with the observed movements and their geological reconstructions.
(3) Since spatial gradients of viscosity complicate main effects of moving continents, viscosity was set to be constant in the model considered.
(4) Although the model allows one to change the shape, sizes and number of continents at each time step, the results presented in this paper describe the evolution of undeformable continents.
(5) Since the computation of a long-term evolution in a 3-D spherical model
requires a high computer performance, whereas all of our computations were
performed on personal computers, a rather rough mesh was used
( R q
q j = 326
j = 326
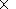 36
36
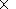 72 and even 16
72 and even 16
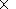 16
16
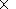 32). However, results calculated
with these meshes are qualitatively similar. The rougher mesh yields a somewhat
smoother distribution of the heat flux and somewhat lower velocities.
32). However, results calculated
with these meshes are qualitatively similar. The rougher mesh yields a somewhat
smoother distribution of the heat flux and somewhat lower velocities.
Notwithstanding its roughness, the model demonstrates the possibility of a self-consistent calculation of a long-term drift of continents and reveals physically reasonable tendencies such as the opening of marginal seas followed by their closing, the opening and development of new oceans, and assemblage of continents into groups corresponding to the largest systems of subduction zones.
The model presented here does not pretend to quantify the detailed evolution of continents. The calculated initial velocities of most continents are consistent with GPS data. However, the velocities of Australia and particularly South America differ from the presently observed values. The model predicts that South America starts moving southeastward rather than northward. This can accounted for by both the assumptions made within the model itself and the disregard of additional effects. Thus, the initial distributions of temperature can involve some uncertainties associated with its calculation on the basis of seismic tomography data.
It is also possible that the inferred southeastward motion of South America implies that this continent, under the action of pressures exerted by the Nazca plate, will the direction of its contemporary motion for the SE direction. However, this cannot occur over a short time interval. Being frozen in the oceanic lithosphere, South America will continue moving northeastward for a certain time. Additional calculations of models with somewhat modified initial conditions, continental thicknesses and the mesh step did not reveal any qualitative changes in the general pattern of the evolution of continents and mantle flow structure.
This study is the first attempt at calculating the future evolution of mantle convection and motions of contemporary continents and islands in terms of a 3-D spherical model of mantle convection with floating continents.
The calculations showed that continents do not move chaotically and passively. Their movement is governed by the equations of transfer of mass, heat, momentum and angular momentum in the mantle-continent system. Moreover, the structure of mantle flows is strongly dependent on the presence and movement of continents.
Since mantle downwellings attract continents floating over the mantle surface, the continents mostly reside above these cold mantle flows and move together with them. Because each mantle downwelling attracts all adjacent continents, continents tend to assemble. This process is enhanced due to the fact that, while continents assemble, the mantle downwellings connected with the continents via viscous forces will also assemble.
Due to the heat-screening effect, mantle heat accumulates beneath the supercontinent. Mantle material becomes lighter, the cold mantle downwellings decay and hot mantle upwellings arise in their place under the supercontinent. Since the heat preferably accumulates beneath the central part of a supercontinent, the latter is typically broken up along its median line.
Evidently, there exist main other processes affecting the formation and breakup of supercontinents. Since continents hinder the heat outflux from the mantle, they partly decrease the intensity of convection, making it less chaotic. Mantle convection makes its interaction with continents more chaotic, whereas continents can be regarded as an ordering factor. In particular, it is due to the direct effect of continents slowly approaching subduction zones that marginal seas open and close.
Thermal convection in a viscous mantle is described by the distributions of the convective velocity vector V i(x, y, z), temperature T(x, y, z) and pressure p(x, y, z). These unknown functions are found from the solution of the following system of three equations of the momentum, heat and mass transfer:
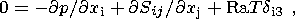 | (1) |
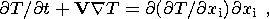 | (2) |
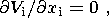 | (3) |
where S ij is the deviatoric tensor of viscous stresses,
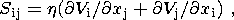 | (4) |
and Ra is the Rayleigh number,
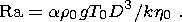 | (5) |
Equations (1)-(3) are written in the Boussinesq approximation in dimensionless
variables. Measurement units are the mantle thickness
D for length,
D/k for
velocity,
D2/k for time,
T0 for temperature,
h0 for viscosity and
h0 k/D2 for
pressure and stresses. Pressure is measured from its hydrostatic
distribution
p(z) defined by the condition
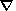 p0=-r0
g.
p0=-r0
g.
A continent is subjected to the action of the gravity force applied to its center of mass and the forces of interaction with a viscous mantle applied to surface elements of the submerged part of the continent. Under the action of these forces, the continent floats in the mantle, moving across its surface and rotating about a vertical axis. Since pressure and velocities of mantle flows vary in time and space, both the vertical velocity of the center of mass of the continent w0 and angular velocities of rotation of the continent wx and wy around instantaneous horizontal axes x and y are generally nonvanishing quantities.
Continents can subside (above mantle downwellings) or rise (above mantle upwellings) together with or relative to the mantle surface. The amounts of subsidence (rise) can differ at different and of the continent. Below we consider solely horizontal movements of the center of mass of the continent and its rotation around a local vertical axis, neglecting all other small effects; i.e. we set w0 = 0 and wx=wy = 0.
Because the gravity force is counterbalanced by the buoyancy force, the external force applied to the continent reduces to the force of viscous coupling with the mantle, with pressure being measured from the hydrostatic distribution p0(z).
The horizontal motion of a solid continent of an arbitrary shape and its rotation around an instantaneous vertical axis are described by Euler equations reducing to a system of three dynamic equations and three kinematic relations [Trubitsyn, 2000b; Trubitsyn and Rykov, 1998b]:
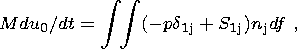 | (6) |
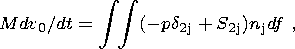 | (7) |
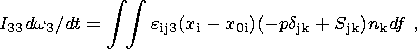 | (8) |
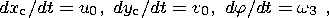 | (9) |
where M is the mass of the continent, I33 is its moment of inertia with respect to the vertical axis, x c(t) and y c(t) are the coordinates of the center of mass of the continent, d ij is the Kronecker delta (equal to 1 at i=j and 0 at i j ) and e ijk is the Levi-Civita symbol (equal to 0 for any two coinciding indexes, 1 for an even permutation of the combination of indexes (123) and - 1 for an odd permutation).
The dimension relations imply that inertial terms on the left-hand side of Euler
equations (6)-(8) and momentum transfer equation (1) are on the order of
kr/m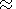 10-23. Therefore, they can be set equal
to zero.
10-23. Therefore, they can be set equal
to zero.
Neglecting the inertial terms, the Euler equations of the motion of continents yield six relations for the determination of the six unknown variables, namely, the coordinates of the center of mass of the continent x c(t) and y c(t), the angle of its rotation j and the velocity components of the continent u0(t), v0(t) and w3(t):
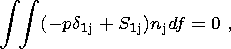 | (10) |
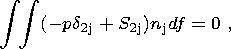 | (11) |
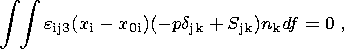 | (12) |
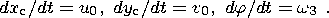 | (13) |
The equations for the distribution of temperature
T c within the solid
continent in the initial immobile system of coordinates reduce to the equation
of heat conduction with the advective heat transport at the velocity of the
continent
Equations of mantle convection (1)-(3) and equations of motion of a continent
(6)-(8) and heat transport inside the continent (14) are interconnected through
boundary conditions.
The impermeability and free-slip conditions are imposed on mantle flows at the
lower and lateral boundaries of the region modeled (if it is finite) and at the
upper boundary outside continents; these conditions imply that the normal
velocity component of the liquid and the tangential components of viscous forces
vanish at the boundaries mentioned:
where
n k is the unit vector normal to a given surface and
t i are unit
vectors tangential to the surface.
The impermeability and no-slip conditions are imposed at the boundaries of
moving solid continents, i.e. velocities of the liquid mantle are equal to
velocities of a continent:
at the entire surface of the part of a continent submerged into the mantle.
The temperature at the lower boundary of the model region is fixed,
T = 1. At
the lateral boundaries (if the region is finite) the heat flux is set at zero:
where
n k is the unit vector normal to the lateral surface of the region.
The mantle temperature is set at zero ( T = 0) at the upper free surface in the
oceanic region outside a continent.
The conditions of continuity of temperature and heat flux is imposed at the
surface of the part of a continent submerged into the mantle:
At the upper surface of the continent, the temperature is set equal to zero:
Thus, the mathematical problem is formulated as follows. There are three unknown
functions of coordinates and time describing mantle convection (the mantle flow
velocity vector
V i(x, y, z, t), temperature distribution
T(x, y, z, t) and pressure
distribution
p(x, y, z, t) ) and four unknown functions
of time describing the motion of
a continent as a whole (two components of the instantaneous velocity of the
translatory motion of the continent's center of mass
u0(t) and
v0(t), one
component of the instantaneous angular velocity of the continent's rotation
around its center of mass
w(t) and the temperature distribution within
the
continent
T c(x, y, z, t) ). These unknown
functions are determined by a
system of interconnected equations: three differential equations of convection
(1)-(3), three integral equations (10)-(12) derived from Euler equations, and
the equation of heat transfer in a continent (14). Knowing at a given time
moment the position and velocities of the continent
u0(t), v0(t) and
w(t), its
position at the next time moment can be found from (9). The constants of
integration of the differential equations are determined from boundary
conditions (14)-(19).
The problem with a freely floating continent differs from the known problem with
an immobile continent in that the boundary conditions for flow velocities and
temperature at the boundary of the mantle and floating continent are updated at
each given time moment, because the velocity and position of the continent are
not known a priori but are found from the solution of the complete system of
interconnected differential equations.
In the case of several continents, equations of motion (10)-(13) and equation
for temperature (14) are written out for each continent. In addition, in the
case of a collision of two continents, the condition of their impenetrability is
imposed. To ensure the validity of this condition at a contact point of the
colliding continents, the forces of viscous coupling with the mantle are
complemented with a force pushing the continents apart that is applied at the
contact point in the direction opposite to the relative velocity vector of the
continents. The magnitude of the push force by a try-and-error technique applied
to the conditions of contact and impenetrability of the continents at a given
time moment.
Anderson, D. L. (1989), Theory of the Earth, p. 366,1989, Blackwell
Scientific Publications,
Boston.
Ekstrom, G., and A. M. Dziewonski (1998), The unique anisotropy of the Pacific upper
mantle, Nature, 394, 168-172.
Forte, A. M., and H. K. C. Perry (2000), Geodynamic evidence for a
chemically depleted
continental tectonosphere, Nature, 290, 1940-1944.
Gurnis, M. (1988), Large-Scale mantle convection and aggregation and dispersal of
Supercontinents,
Nature, 332, 696-699.
Gurnis, M., and Sh. Zhong (1991), Generation of long wavelength Heterogeneity's in
the mantle dynamics
interaction between plates and convection, Geophys. Res. Lett., 18, 581-584.
Kaban, M. K., and P. Schwintzer (2000), Seismic Tomography and Implications
for Models of the Earth's Mantle, Geoforschung Zentrum (Scientific Technical
Report
STR00/01), Potsdam.
Lowman, J. P., and J. T. Jarvis (1993), Mantle convection flow reversal due to
continental collisions, Geophys. Res. Lett., 20, 2087-2090.
Lowman, J. P., and J. T. Jarvis (1996), Continental collisions in wide aspect ratio
and
high Rayleigh number two-dimensional mantle convection models, J. Geophys. Res.
101, 25,485-25,497.
McCulloch, M. T., and V. C. Bennett (1998), Early differentiation of the Earth: an
isotopic perspective, in The Earth's mantle, edited by I. Jackson, Cambridge
University Press.
Nakanuki, T., D. A. Yuen, and S. Honda (1997), The interaction of plumes with
transition
zones under continents and oceans, Earth Planet. Sci. Lett., 146, 379-391.
Schubert G., D. L. Turcotte, and P. Olson (2001), Mantle Convection in the
Earth and Planets, p. 940, Cambridge Univ. Press.
Solheim, L. P., and W. R. Peltier (1994), Phase boundary deflections at 660-km depth
and
episodically layered isochemical convection in the mantle, J. Geophys. Res.,
99, 15,861-15,875.
Tackley, P. J. (1996), Effects of strongly variable viscosity on three-dimensional
compressible convection in planetary planets, J. Geophys. Res., 101, 3311-3332.
Tackley, P. J. (2000), Mantle convection and plate tectonics: Toward an integrated
physical and chemical theory, Science Print, 2888, 2002-2007.
Tackley, P. J., D. J. Stevenson, G. A. Glatzmaier, and G. Schubert
(1994), Effect of
multiple phase transitions in three dimension spherical model of convection in
Earth's mantle, J. Geophys. Res., 99, 15,877-15,901.
Trubitsyn, V. P. (2000a), Phase transitions, compressibility, thermal expansion,
and
adiabatic temperature in the mantle, Izvestiya, Phys. Solid Earth, 36, 101-113.
Trubitsyn, V. P. (2000b), Principles of the tectonics of floating continents,
Izvestiya, Phys. Solid Earth, 36, 101-113.
Trubitsyn, V. P., and A. S. Fradkov (1985), Convection under continents and oceans,
Izvestia, Phys. Solid Earth, 21, 491-498.
Trubitsyn, V. P., and A. M. Bobrov (1994), Evolution of the mantle convection after
breakup of a supercontinent, Izvestia, Phys. Solid Earth, 29, 768-778.
Trubitsyn, V. P., and V. V. Rykov (1995), A 3-D numerical model of the Wilson cycle,
J. Geodyn., 20, 63-75.
Trubitsyn, V. P., and V. V. Rykov (1998a), A self-consistent 2-D model of mantle
convection
with a floating continent, Russian J. Earth Sci., 1(1).
http://rjes.wdcb.ru/v01/tje98001/tje98001.htm
Trubitsyn, V. P., and V. V. Rykov (1998b), 3-D spherical models for mantle convection,
continental drift, and the formation and disintegration of supercontinents,
Russian J. Earth Sci., 1(2).
http://rjes.wdcb.ru/v01/tje98005/tje98005.htm
Trubitsyn, V. P., V. V. Rykov, and W. Jacoby (1999), A self-consistent 2-D model
for
the dip angle of mantle downflow beneath an overriding continent,
J. Geodyn., 28, 215-224.
Trubitsyn, V. P., and V. V. Rykov (2000), 3-D Spherical Models of Mantle Convection
with Floating Continents, (U.S. Geological Survey Open File Report 00-218,
88).
Trubitsyn, V. P., W. D. Mooney, and D. A. Abbott (2003), Cool cratons and
thermal
blankets: How continents affect mantle convection, Int. Geol. Rev., 45, 479-496.
Turcotte, D. L., and G. Schubert (1982), Geodynamics: Applications of Continuum
Physics to Geological Problems, 449 pp., John Wiley, New York.
Zhong, Sh., and M. Gurnis (1994), Role of plates and temperature-dependent viscosity
in
phase change dynamics, J. Geophys. Res., 99, 15,903-15,917.
Zhong, Sh., M. T. Zuber, L. Moresi, and M. Gurnis (2000), Role of temperature-dependent
viscosity and surface plates in spherical shell models of mantle convection,
J. Geophys. Res., 105,
11,063-11,082.
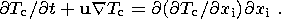
(14) 1.3. Boundary Conditions
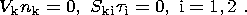
(15) 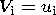
(16) 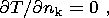
(17) 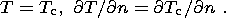
(18) 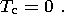
(19) Appendix 2: Electronic Supplement (JavaScript-Based
Animation)
The calculated evolution of continents is presented in details on three hundred of
images (frames) showing the corresponding instantaneous convection
pattern and position of continents. The number of each frame corresponds
approximately to the time moment in millions of years (Myr). The set of frames
is managed by the client-side JavaScript program developed by the publisher for this
particular task. The program can be started online or offline and has user-friendly
interface. Reader can browse frames forth and back, select any particular frame
and run the set of frames as JavaScript-based animation (Animation 1).

Animation 1
Acknowledgments
This work was supported by the Russian Foundation for Basic Research, project
no. 02-05-64723B; the Moscow Research and Technology Center, project no. 1538;
and the Ministry of Education and Science, project no. 43.043.1.1.1601.
References
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.1.3) on December 18, 2004.