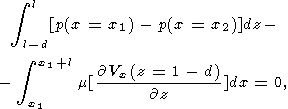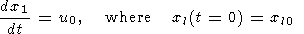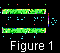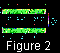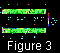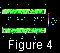Russian Journal of Earth Sciences
Vol 1, No. 1, July 1998
Translated December 1998
A Self-Consistent 2D Model of Mantle Convection with a Floating
Continent
V. P. Trubitsyn and V. V. Rykov
Shcmidt United Institute of Physics of the Earth, Russian Academy
of
Sciences, B. Gruzinskaya ul. 10, Moscow, 123810 Russia
Contents
Abstract
The mantle is modeled by a viscous fluid filling a horizontally elongated
2D region with an aspect ratio of 10:1. A model with Ra = 10
6 is
constructed on a 200
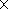 80 mesh. Developed nonsteady-state thermal
convection including narrow downwellings and upwellings sets in, with
mantle flow velocities ranging from 1 to 10 cm/yr. Then, at a certain
moment, a continent floating on the mantle is introduced into the model.
The continent is modeled by a thin long plate of a thickness of 0.03 and a
length of 2.0 relative units with respect to the mantle thickness, which
corresponds to dimensional values of 90 and 6000 km, respectively. To
demonstrate mantle heating beneath continent, the latter is positioned at
the coldest place of the mantle where downgoing flows dominate at the
moment chosen. The evolution of the mantle-continent system is found
from numerical solution of equations governing the momentum, mass, and
heat transfer in viscous fluid and rigid continent. The problem is rigorously
formulated, a self-consistent method is given for the solution of coupled
integrodifferential equations, and a technique of their numerical
implementation is described. The continent remains virtually immobile
during a long time (about 500 Ma), but the mantle flow pattern
dramatically changes, which results in suppression of cold mantle
downwellings under the continent and their gradual replacement by hot
upwellings. Afterwards the viscous drag of mantle flows begins to move the
continent at a variable velocity averaging about 1 cm/yr. The mantle flow
pattern and continent velocity constantly changes under the action of
mechanical coupling and thermal interaction between the mantle and
moving continent. After a time of about
1.5
80 mesh. Developed nonsteady-state thermal
convection including narrow downwellings and upwellings sets in, with
mantle flow velocities ranging from 1 to 10 cm/yr. Then, at a certain
moment, a continent floating on the mantle is introduced into the model.
The continent is modeled by a thin long plate of a thickness of 0.03 and a
length of 2.0 relative units with respect to the mantle thickness, which
corresponds to dimensional values of 90 and 6000 km, respectively. To
demonstrate mantle heating beneath continent, the latter is positioned at
the coldest place of the mantle where downgoing flows dominate at the
moment chosen. The evolution of the mantle-continent system is found
from numerical solution of equations governing the momentum, mass, and
heat transfer in viscous fluid and rigid continent. The problem is rigorously
formulated, a self-consistent method is given for the solution of coupled
integrodifferential equations, and a technique of their numerical
implementation is described. The continent remains virtually immobile
during a long time (about 500 Ma), but the mantle flow pattern
dramatically changes, which results in suppression of cold mantle
downwellings under the continent and their gradual replacement by hot
upwellings. Afterwards the viscous drag of mantle flows begins to move the
continent at a variable velocity averaging about 1 cm/yr. The mantle flow
pattern and continent velocity constantly changes under the action of
mechanical coupling and thermal interaction between the mantle and
moving continent. After a time of about
1.5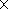 109, when the continent
has traveled over a distance of about 15000 km, it arrives at a place where
several cold mantle downwellings concentrate. Then the continent velocity
sharply decreases, and the continent continues its motion in either primary
or opposite direction, depending on the general mantle flow pattern. The
results of the numerical experiment can be used for the analysis of
mechanism responsible for the motion of Eurasia-type continents,
origination and ascent of plumes, and geodynamic processes in the
subcontinental mantle.
109, when the continent
has traveled over a distance of about 15000 km, it arrives at a place where
several cold mantle downwellings concentrate. Then the continent velocity
sharply decreases, and the continent continues its motion in either primary
or opposite direction, depending on the general mantle flow pattern. The
results of the numerical experiment can be used for the analysis of
mechanism responsible for the motion of Eurasia-type continents,
origination and ascent of plumes, and geodynamic processes in the
subcontinental mantle.
1. Introduction
Presently, various numerical experiments have been used for the study of
thermal convection in the Earthºs mantle. The role of variable,
temperature-dependent viscosity, pressure and temperature, as well as the
effect of phase transformations on the mantle flow pattern, have been
examined in terms of 2D and 3D models in Cartesian and spherical
coordinates (see e.g. [Christensen, 1983, 1984;
Christensen and Yuen, 1984; Glatzmaier, 1988;
Machetel and Weber, 1991; Lenardic and Kaula,
1994; Solheim and Peltier,
1994; Tackley et al., 1994;
Parmentier et al., 1994]). Numerical modeling has provided
an insight into many basic
regularities of global geodynamics. In the nearest decade, a numerical
modeling problem of vital importance is the construction of self-consistent
models in which oceanic high-viscosity lithosphere breaks into separate
plates.
Another important problem is the exploration of the effect of continents on
the mantle convection structure. Continents cover more than a quarter of
the Earth's surface. The mantle heat flow in continental areas is about 30
mW/m
2, which is one-third as much as the heat flow in oceanic areas,
averaging 90 mW/m
2. This is explained by the fact that continents are
thermal insulators of the mantle, because only the conductive mechanism
of heat transfer is operative within continents. Various estimates of the
Nusselt number, characterizing the whole-mantle convective heat loss,
give a value of about 20. The oceanic lithosphere, involved in the
convective circulation of matter, virtually remains within the convective
thermal boundary layer and, despite its high viscosity, cannot serve as an
effective thermal screen for the mantle. Thus, even immobile continents
should considerably affect the structure of mantle convection.
Based on a simplified model, Christensen, [1983] compared
the mantle
flow patterns beneath continents and oceans. Trubitsyn and Fradkov, [1985]
showed that thermal convection in the upper mantle is suppressed,
resulting in a threefold decrease in the continental heat flow. As was
shown in later works [Trubitsyn et al., 1993a, 1993b,
1994; Trubitsyn and Bobrov,
1993; 1996, 1997;
Lowman and Jarvis, 1993, 1995,
1996; Bobrov and Trubitsyn, 1996;
Nakakuki et al., 1997], an immobile
continent initially suppresses the underlying mantle convection and
broadens the convective cell; afterwards, when the subcontinental mantle
had been heated during the following few hundreds of millions of years, a
hot upwelling mantle flow develops beneath the continent.
Since continents are not fixed but float on the mantle, their effect on the
mantle convection structure is even greater. In early studies, the effect of
continental drift was included in a simplified form, as an effective
boundary condition. In continental areas, the free upper boundary
condition was replaced by fixed values of horizontal velocity [Lux et al.,
1979]. In a similar manner, Doin M.-P., [1997]
simulated the effect of moving
continents by a time-dependent velocity specified at the upper boundary.
Gurnis, [1988] presented the results of a consistent
numerical 2D model of
mantle convection with free floating continents. For the first time, a
numerical 3D model of mantle convection with two floating continents was
constructed by Trubitsyn and Rykov, [1995] and Rykov
and Trubitsyn, 1996a,
1996b]. This model reconstructs general regularities of the
formation and breakup of Pangea [Trubitsyn and Rykov, 1995].
Structures
similar to the Atlantic and Pacific oceans form upon the Pangea breakup.
In terms of this model, a very steep subduction zone (of the Kuril-Kamchatka
type) develops at one of the Pacific margin, and a very gently
dipping subduction zone (of the South American type) develops at the
other. Assuming an alternative initial position of continents, Rykov and Trubitsyn,
[1996b] obtained a structure consisting of two coupled
continents (similar to North and South Americas), which developed upon
the breakup of a supercontinent.
Trubitsyn and Rykov, [1997] developed a self-consistent
numerical model
of low-Ra convection in the upper mantle having a variable viscosity and
interacting with a moving continent modeled by a thick rigid plate. The
cases with a free plate floating over the mantle and moving at a prescribed
fixed velocity were considered. The continent approaching a downgoing
cold mantle flow was found to deflect this flow and form structures similar
to inclined subduction zones. The dip angle of the downgoing mantle flow
decreases with the velocity of the approaching continent.
This work describes in detail the mathematical formulation of the problem
and the method of its solution. A Ra = 10
6 convection model close to
the real Earth is constructed on a 200
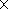 80 mesh, including a thin
continent of thickness
d = 90 km and horizontal size
l = 6000 km. The
long-term evolution of the mantle-continent system is calculated.
Comparison of the evolution of unsteady-state convection in the mantle
with and without a continent shows that the moving continent dramatically
changes the mantle convection structure.
80 mesh, including a thin
continent of thickness
d = 90 km and horizontal size
l = 6000 km. The
long-term evolution of the mantle-continent system is calculated.
Comparison of the evolution of unsteady-state convection in the mantle
with and without a continent shows that the moving continent dramatically
changes the mantle convection structure.
2. Model
The mantle is modeled by an incompressible constant-viscosity fluid
occupying the volume of an elongated rectangular 2D layer of a thickness
D and length
L, with the aspect ratio
L:D=10:1. The upper
boundary is assumed to be free and other boundaries are impermeable,
with a slip condition. The lower and upper boundaries have fixed
temperatures
T=T0 and
T=0, respectively; i.e. the layer is
heated from below. The side walls are thermally insulated. The coordinate
origin coincides with the left-hand lower corner, the
z axis is directed
upward, and the
x axis is directed to the right.
Continents are represented as light rigid rectangular thick plates that are
heat conductive, float in the mantle, and have the length
l and thickness
d+d0, where
d is the depth to which the continent is immersed in
the mantle and
d0 is the continent elevation above the mantle. The
viscous coupling with mantle flows drives the continent toward downgoing
mantle flows. Because the heat transfer mechanism within continents is
purely conductive, the continents produce a heat insulating effect which
prevents heat to escape from the mantle. Also, the continents affect
mechanically the mantle, because the no-slip condition tends to attenuate
velocity contrasts in mantle flows adjacent to the lateral and lower
boundaries of the continents.
3. The System of Equations of Mantle Convection with
Floating
Continents
3.1. Equations of thermal convection
Thermal convection in a viscous mantle is described by the distributions of
convective vector velocities
Vi(x, y, z), temperature
T(x, y, z),
and pressure
p(x, y, z). These unknown functions are
found from the solution of three equations of momentum, heat, and mass transfer
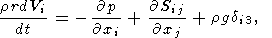 | (1) |
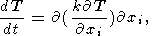 | (2) |
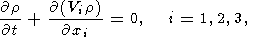 | (3) |
where
r is density,
g is gravity,
T is temperature measured from
the adiabatic distribution,
k is diffusivity,
dij is the Kronecker
delta, and
Sij is the deviator tensor of viscous stresses
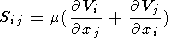 | (4) |
Here
m is viscosity. The relative values of inertial
terms in the left-hand
side of mantle momentum transfer equation (1) are of the order of
kr /m 10-23 with respect to the
right-hand terms. Therefore, these
inertial terms may be neglected.
10-23 with respect to the
right-hand terms. Therefore, these
inertial terms may be neglected.
We put
r = r0(1
- a) in the buoyancy term of equation (1) and
r = r0
in other terms of equations (1)-(2). Hereinafter the pressure is measured
from its hydrostatic distribution
p0(z) determined from the
condition
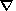 p = -r0g.
Also, we introduce dimensionless variables
taking, as measurements units, the mantle thickness
D for length,
k/D for velocity,
D2/k for time,
T0 for temperature,
m
for viscosity, and
mk/D2 for pressure and
stresses.
p = -r0g.
Also, we introduce dimensionless variables
taking, as measurements units, the mantle thickness
D for length,
k/D for velocity,
D2/k for time,
T0 for temperature,
m
for viscosity, and
mk/D2 for pressure and
stresses.
Using these variables, 2D model equations of convection (2)-(4) take the
form
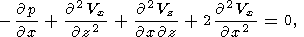 | (5) |
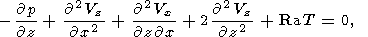 | (6) |
 | (7) |
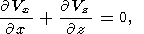 | (8) |
where Ra is Rayleigh number,
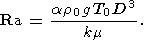 | (9) |
3.2. Equations of motion of a continent
In a 2D model, velocities
u=(ux, uy) at all points
of a rigid continent
floating in the mantle (along its horizontal surface) have the same values
and are equal to the velocity of its center of gravity:
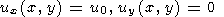 | (10) |
The continents move under the action of viscous forces of mantle flows.
The Euler equations of horizontal movement of a rigid continent have the
form
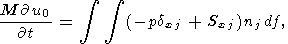 | (11) |
where
df is the elementary area of the surface,
nj is the unit vector
of outward normal to the area, and
M is the dimensionless mass of the
continent, referred to the unit length of the
y axis in the 2D model
considered. The integral is taken over the whole surface of the continent
portion immersed in the mantle, which includes its base
(z=1-d) and
side walls ( x=x1 and
x=x1+l ):
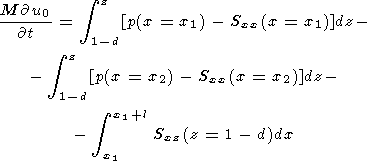 | (12) |
where
d and
l are thickness and length of the immersed portion of
continent;
x1(t) and
x2(t)=x1(t)+l are instantaneous
coordinates of the
left- and right-hand walls of the continent, which obey the conditions
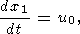 | (13) |
The equation governing the temperature distribution
Tc within the
rigid continent in the initial fixed system of coordinates is reduced to the
equation of heat conductivity with advective heat transfer controlled by the
continent velocity
u0 along
x axis,
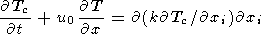 | (14) |
Similar to the mantle, the relative value of inertial terms in the left-hand
side of the equation of continent motion (12) is of the order of
kr/m 10-23 compared to the
terms in its right-hand side. Substituting deviator
tensor of viscous stresses (4) into (12) and omitting inertial terms, we
obtain the equations of continent motion in dimensionless variables
10-23 compared to the
terms in its right-hand side. Substituting deviator
tensor of viscous stresses (4) into (12) and omitting inertial terms, we
obtain the equations of continent motion in dimensionless variables
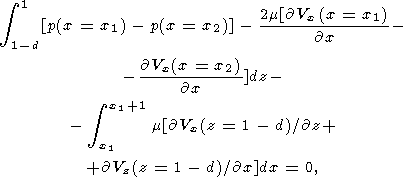 | (15) |
where the coordinate
x1 in the integration limits is determined from
(13).
3.3. Boundary conditions
Equations of mantle convection (6)-(10), continent motion (15) and (13),
and heat transfer within the continent (14) are interconnected through
boundary conditions.
Temperature boundary conditions at the lower and lateral boundaries of
the whole area studied have the form
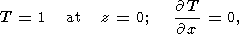 | (16) |
at
x=0 and
x=10.
The mantle temperature at the free upper,
z=1, surface vanishes (( T=0 )
only in the oceanic area, outside the continent, namely ( x < x1(t) and
x > x1(t)+l ).
At the continental surface immersed in the mantle, the temperature and
heat flow are set to be continuous between the mantle and continent; i.e.,
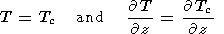 | (17) |
at the base of the continent,
z=1-d and
x1(t) < x < x1(t)+l,
and
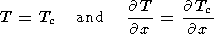 | (18) |
at its lateral surface sections,
1-d < z < 1 and
x = x1 or
x = x2.
Zero temperature is set on the upper surface of the continent, i.e.,
Tc = 0 at
x1(t) < x < x1(t)+l and
z=1 + d0, where
d0 is the elevation of the
continent above mantle surface (commonly,
d0 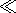 d ).
d ).
As noted above, impermeability and slip conditions are imposed on mantle
flows on the lower and lateral boundaries of the entire calculated region.
Therefore, the lower boundary condition is
Vz = 0,
Sxz = 0 at
z = 0.
Because it is valid at all
x, we have
Vz/x = 0 at
z = 0. In view of
(4), we obtain
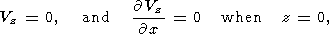 | (19) |
Similar conditions are imposed on the lateral boundaries,
 | (20) |
Condition (19) is also imposed on the free upper surface
z =1 outside
the continent:
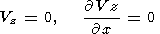 | (21) |
at
x < x1(t) and
x > x1(t)+l.
The non-slip condition on the interface between the viscous mantle and
moving continent implies that the velocities of mantle flow and continent
motion coincide on this boundary:
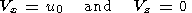 | (22) |
at the base of the continent for
x1(t) < x < x1(t) + l and
z = 1 - d and at
its wall sections for
1-d < z < 1,
x = x1 and
x = x2.
Conditions (22) simplify the equation of continent motion. Since the
impermeability condition is satisfied all along the base of the continent
irrespective of
x, we also have
Vz = 0 at the base. Consequently, the
last term under the integral sign in (15) vanishes. Likewise, since the no-slip
condition
Vz = 0 is satisfied all over the walls of the continent
irrespective of
z, we have
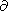 Vz/
Vz/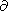 z=0. Then, incompressibility condition
(8) implies that
z=0. Then, incompressibility condition
(8) implies that
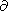 Vx/
Vx/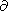 x=0 on the walls. As a result, the equations of
continent motion assume a simple form
x=0 on the walls. As a result, the equations of
continent motion assume a simple form
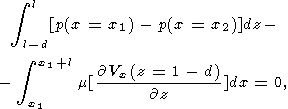 | (23) |
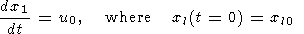 | (24) |
Finally, the resulting mathematical problem may be stated as follows. In
all, there are seven unknown functions. These are four position- and time-dependent
functions for the mantle convection: two velocity components
of mantle flows
Vx(x, z, t) and
Vz(x, z, t), temperature distribution
T(x, z, t), and pressure distribution
p(x, z, t), and three functions for the
continent: temperature distribution within the continent
Tá(x, z, t),
instantaneous translational velocity of the continent as a whole
u0(t),
and the coordinate of its left-hand edge
x1(t). These functions can be
found from a closed system of seven coupled equations: four differential
equations of convection (5)-(8), thermal conductivity equation for the
continent (14), and the equation of motion of the rigid continent, which is
reduced to the condition imposed on mantle flow velocity derivatives (23)
and to relation (24) between the velocity of the continent and its position.
The constants of integration of the differential equations are found from
boundary conditions (18)-(22).
The difference between our problem with a free floating continent and the
well-known problem with a fixed continent consists in the fact that the
impermeability and no-slip conditions on the upper surface must be
satisfied at the place currently occupied by the floating continent whose
velocity and position are not a priori known but should be defined by
solving the system of coupled differential equations at each time step.
4. Numerical Method
Two basically different methods are applicable to the solution of the
system of thermal convection equations including floating continents. In
the two-region method [Trubitsyn and Bobrov, 1996, 1997],
equations of
heat and mass transfer are solved at each time step separately outside and
within the continent, and continuity conditions are then set at the interface
between continent and mantle. In the one-region region [Trubitsyn and Rykov,
1995;
Rykov and Trubitsyn, 1996a, 1996b],
computations are
conducted in a single coherent domain and explicitly incorporate the jump
in material properties between mantle and continents on the surface of the
continent.
The numerical algorithm solving the system of thermal convection
equations including floating continents can be summarized as follows. Let
convective flow velocities and mantle distributions of temperature
T(t1) and pressure
p(t1), as well as position
x1(t1) and
velocity
u0(t1) of the continent, be known at a time
moment
t1.
We have to find the solution of system (5)-(8), (14), (23) and (24) at the
next time moment
t2 = t1 + Dt.
The new position of the continent
x1(t2) at the moment
t2 is readily found from (24):
x1(t2) = x1(t1)
+ u0(t)1)Dt. If
the continent velocity at this moment
u0(t2) were also
known, one could solve thermal convection equations (5)-(8) with
boundary conditions for temperature (18) and velocities (19)-(22),
consistent with the new position of the continent, and find mantle flow
velocities
Vx(t2) ¨
Vz(t2), temperature
T(t2) and pressure
p(t2)
at the time moment
t2. However, the complexity of the problem lies
just in the fact that the velocity of the continent
u0(t2) is unknown. Its
value must comply with mantle flow velocities
Vx(t2) and
Vz(t2)
that obey equation of continent motion (24). Therefore, an iterative
technique should be developed for determining this velocity of the
continent. In principle, based on continent velocity values chosen in
accordance with a specified enumeration procedure, convective velocity
fields and integrals in (23) can be calculated until a value of
u0(t2) is
found for which the right-hand side of (23) deviates from zero by a
quantity
e complying with desired accuracy. Since the right-hand
side physically represents the force that acts on the continent, we have
e > 0 if the chosen velocity of the continent
u0(t2) is underestimated and
e< 0 if it is overestimated.
A finite difference method was used for solving the system of equations of
thermal convection including floating continents [Rykov and Trubitsyn, 1996b]. Numerical solution of temperature transfer equation (7)
or (14)
employed the flux-corrected transport method of Zalesak, [1979].
Equations for velocities and pressure (5), (6) and (8) were reduced to
elliptic equations with variable coefficients (generalized Poisson
equations). They were solved with the help of the three-layer triangular
method with a conjugate-gradient choice of iteration parameters
[Samarskii and Nikolaev, 1978].
5. Numerical Results
5.1. Free nonsteady-state mantle convection
The mantle was modeled by a viscous fluid that occupies an elongated 2D
region. Given the mantle thickness
D  3000 km, its outer
circumference
2pR
3000 km, its outer
circumference
2pR  40000 km, and its inner circumference
2p (R-D)
40000 km, and its inner circumference
2p (R-D)  21000 km, the region approximating the mantle had an aspect ratio
of
L:D = 10:1. The simplest, Ra=
106 model with heating from
below was computed on a
200
21000 km, the region approximating the mantle had an aspect ratio
of
L:D = 10:1. The simplest, Ra=
106 model with heating from
below was computed on a
200 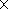 80.
80.
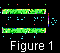
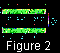
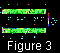
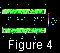 Figures 1a,
2a,
3a,
and 4a
present model patterns of the mantle thermal convection
developed after the dimensionless time moment
t =1.0995. As is
known, the whole region, even with no convection, is heated throughout at
t > 1. Therefore, we may consider the convection as well-developed by
that moment. However, at Ra
> 2
Figures 1a,
2a,
3a,
and 4a
present model patterns of the mantle thermal convection
developed after the dimensionless time moment
t =1.0995. As is
known, the whole region, even with no convection, is heated throughout at
t > 1. Therefore, we may consider the convection as well-developed by
that moment. However, at Ra
> 2 105 thermal convection is
nonstationary and quasi-turbulent, because the nonlinear terms
Vx
105 thermal convection is
nonstationary and quasi-turbulent, because the nonlinear terms
Vx T/
T/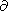 x and
Vz
x and
Vz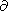 T/
T/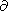 z in (7) generate new, smaller-degree harmonics at each time
step. With increasing Rayleigh number, these nonlinear terms become
larger, and smaller-scale time-variable inhomogeneities arise as a result of
self-organization.
z in (7) generate new, smaller-degree harmonics at each time
step. With increasing Rayleigh number, these nonlinear terms become
larger, and smaller-scale time-variable inhomogeneities arise as a result of
self-organization.
The dimensionless temperature equal to
T=0 at the upper surface and
to
T0=1 at the lower one is shown in the figure by variable shades.
The magnitude and direction of the mantle flow velocity at each point are
indicated by an arrow. Velocity scales are shown in the lower right-hand
corners of the figures. Maximum dimensionless values of the velocities are
V max  1500.
1500.
The thin (red in the on-line color figure version) line in the upper part of
the figures shows the inferred distribution of the Nusselt number
(dimensionless heat flow
q = -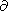 T/
T/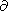 z ) over the
external surface of the region.
The mean Nusselt number is Nu
z ) over the
external surface of the region.
The mean Nusselt number is Nu
 17. The amplitude of relative
variations in the heat flow is about 100%.
17. The amplitude of relative
variations in the heat flow is about 100%.
The thick (green in the on-line color figure version) line shows the inferred
topography, i.e., deformations of the upper free surface arising under the
action of viscous convection stresses. The scale of dimensionless relief
elevations multiplied by a factor of
10-3 is shown on the right-hand axis.
The elevations were estimated from the formula
h = Szz/rg.
Taking into
account the stress unit defined in Section 3, the relief elevation unit is
mk/(rgD2).
As seen from Figures 1a, 2a, 3a, and 4a, mean amplitudes of the dimensionless elevations are of an order
of
25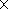 103.
103.
Setting, for the Earth,
D  3 106 m,
a
3 106 m,
a 3 10-5
K-1,
DT
3 10-5
K-1,
DT  2 103 K,
k
2 103 K,
k  10-6 m2 s-1,
m
10-6 m2 s-1,
m 1022
Pa s,
r
1022
Pa s,
r 5 103
kg/m3, and
g
5 103
kg/m3, and
g  10 m s-2,
the time and velocity units can
be found. The velocity unit is
k/D
10 m s-2,
the time and velocity units can
be found. The velocity unit is
k/D  10-5
m/yr, and the time unit is
t=D2/k
10-5
m/yr, and the time unit is
t=D2/k  3
3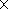 1011
years. According to (9), the Rayleigh
number, which characterizes the intensity of mantle thermal convection, is
Ra
1011
years. According to (9), the Rayleigh
number, which characterizes the intensity of mantle thermal convection, is
Ra  8 106.
8 106.
Since the above parameters of the Earth are not accurate enough, we used
an approximate Rayleigh number Ra =
106. Since mantle flow velocities
obey the proportionality relation
V 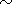 Ra
2/3 [Turcotte and Schubert, 1982],
the velocities and times can easily obtained for somewhat different
Rayleigh numbers. With the Earth parameters specified above, the inferred
results and observed data may be compared if the velocity values are
multiplied by
82/3 = 4 and the time is divided by 4. As a result, maximum
mantle flows have
V max
Ra
2/3 [Turcotte and Schubert, 1982],
the velocities and times can easily obtained for somewhat different
Rayleigh numbers. With the Earth parameters specified above, the inferred
results and observed data may be compared if the velocity values are
multiplied by
82/3 = 4 and the time is divided by 4. As a result, maximum
mantle flows have
V max  1500
1500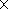 4
4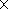 10-5
m/yr
10-5
m/yr
 6 cm/yr.
6 cm/yr.
Figures 1a, 2a, 3a, and 4a illustrate the inferred evolution of mantle convection
over a
large time interval. The dimensionless times are indicated in the left-hand
parts of the figures. As noted above, the unit time is
t 3
3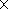 1011
years. In order to calculate the time interval between the convection states
shown in Figures, the dimensionless times indicated in the figures
should be multiplied by
3
1011
years. In order to calculate the time interval between the convection states
shown in Figures, the dimensionless times indicated in the figures
should be multiplied by
3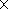 1011 years and divide
by 4 (due to Rayleigh
number rescaling); i.e., the dimensionless times should be multiplied by
75
1011 years and divide
by 4 (due to Rayleigh
number rescaling); i.e., the dimensionless times should be multiplied by
75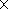 109 years. Then, the overall evolution
time of mantle convection
shown in Figures is
(1.1495 - 1.0995)
109 years. Then, the overall evolution
time of mantle convection
shown in Figures is
(1.1495 - 1.0995)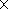 75
75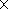 109 years
109 years
 3.6
3.6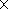 109 years.
109 years.
The relief elevation unit is
mk/(rgD2)
 0.02 m so that dimensionless
amplitudes of inferred relief elevations of
2.5
0.02 m so that dimensionless
amplitudes of inferred relief elevations of
2.5  104 correspond to 0.5
km.
104 correspond to 0.5
km.
5.2. Evolution of the mantle convection with a floating continent
Figures 1b, 2b, 3b, and 4b present the inferred mantle convection patterns including
thermal and mechanical interaction effects with a moving continent. For
comparison, Figures 1a,
2a,
3a,
4a
and Figures 1b,
2b,
3b,
4b
show the
patterns calculated at the
same time moments. A continent represented by a rigid plate of the
thickness
d=0.03
D=90 km and length
l=2
D= 6000 km is
introduced at the time moment
t=1.0995. In Figures 1b, 2b, 3b, and 4b, the
continent is shown by gray. It is intentionally chosen to initially occupy the
coldest place in the mantle where outgoing mantle flows are most
abundant. The figures show that, due to the heat-insulating effect, the
mantle under the continent is gradually heated. By the time
t=1.1151  1.2
1.2 109 years, a well-defined system
of hot mantle upwellings has
formed under the continent, and the continent starts drifting to the right
under the action of mantle flow viscous drag force. Since the continent at
each moment interacts with mantle flows, the mantle convection structure
changes as the continent moves. The dimensionless continental drift
velocity first increases from 100 to 400 and then decreases. According to
the definitions made above, dimensional velocities range from 0.4 to 1.6
cm/yr. As seen from Figures 1b, 2b, 3b, and 4b, after two billion years, when the
continent had traveled a distance of about 5
D
109 years, a well-defined system
of hot mantle upwellings has
formed under the continent, and the continent starts drifting to the right
under the action of mantle flow viscous drag force. Since the continent at
each moment interacts with mantle flows, the mantle convection structure
changes as the continent moves. The dimensionless continental drift
velocity first increases from 100 to 400 and then decreases. According to
the definitions made above, dimensional velocities range from 0.4 to 1.6
cm/yr. As seen from Figures 1b, 2b, 3b, and 4b, after two billion years, when the
continent had traveled a distance of about 5
D  15000 km, it nearly
stops.
15000 km, it nearly
stops.
 In the on-line version of this paper, Figures 1a, 2a, 3a, 4a and 1b, 2b, 3b, 4b are
complimented by movies (Figure 5 and Figure 6, respectively), each including 30
frames.
In the on-line version of this paper, Figures 1a, 2a, 3a, 4a and 1b, 2b, 3b, 4b are
complimented by movies (Figure 5 and Figure 6, respectively), each including 30
frames.
6. Conclusion
The evolution of free unstable-state mantle convection and evolution of
mantle convection coupled with a free floating continent were calculated.
The comparison of concurrent distributions of temperature and mantle flow
velocities derived from these two models has demonstrated that floating
continents dramatically change the structure and evolution of mantle
convection. Detailed evolution results presented in this paper are useful for
investigations into the driving mechanism of Eurasia-type continent
motion, plume origination and upwelling, and thermal regime of
subcontinental mantle.
Acknowledgments
This work was supported by the International Center of Research and
Technology, Grant No. 415-96 and the Russian Foundation for Basic
Research, Project No. 96-05-66069.
References
Bobrov A. M., Trubitsyn V. P., Physics of the Earth, N. 7, 1995, p. 5-13
(in Russian).
Bobrov. A. M., Trubitsyn V. P., Times of rebuilding of mantle flows
beneath continent, Izvestiya, Physics of the Solid Earth, 31, 1996,
pp. 551-559.
Christensen U., A numerical model of coupled subcontinental and oceanic
convection, Tectonophysics, 95, 1983, pp. 1 - 23.
Christensen U. R., Convection wih pressure- and temperature-dependent
non-Newtonian rheology, Geophys. J. Astr. Soc., 77, 1984, pp. 343-384.
Christensen U. R. and Yuen D. A., The interaction of a subducting lithospheric
slab with a chemical or phase boundary, J. Geophys. Res., 89, 1984, pp.
4389-4402.
Doin M.-P., Fleitout L. and Christensen U., Mantle convection and stability of
depleted and undepleted continental lithosphere, J. Geophys. Res., 102,
1997, pp. 2771-2787.
Glatzmaier G. A., Numerical simulation of mantle convection:
Time-dependent, three-dimensional, compressible, spherical shell, Geophys. astrophys.
Fluid Dyn., 43, 1988, pp. 223-264.
Guillou, L. and Jaupart C., On the effect of continents on mantle convection,
J. Geophys. Res., 100, 1995, pp. 24217-24238.
Gurnis M., Large-scale mantle convection and aggregation and dispersal of
supercontinents, Nature, 332, 1988, pp. 696-699.
Gurnis M. and Zhong S., Generation of long wavelengh heterogeneitiey in the
mantle dynamics interaction between plates and convection, Geophys. Res. Lett.,
18, 1991, pp. 581-584.
Lenardic A. and Kaula W. M., Tectonic plates, D
" thermal structure, and
the nature of mantle plumes, J. Geophys. Res., 99, 1994, pp.
15697-15708.
Lowman J. P. and Jarvis J. T., Mantle convection flow reversals due to
continental collisions, Geophys. Res. Lett., 20, 1993, pp. 2091-2094.
Lowman J. P. and Jarvis J. T., Mantle convection models of continental
collision and breakup incorporating finite thickness plates, Phys. Earth Planet.
Inter., 88, 1995, pp. 53068.
Lowman J. P. and Jarvis J. T., Continental collisions in wide aspect ratio and
high Rayleigh number two-dimensional mantle convection models, J. Geophys. Res.,
101, B11, 1996, pp. 25485-25497.
Lux R. A. Davies G. F. and Thomas J. H., Moving lithospheric plates and mantle
convection, Geophys. J. R. Astron. Soc., 57, 1979, pp. 209-228.
Machetel P. and Weber P., Intermittent layered convection in amodel mantle
with an endothermic phase change at 670 km, Nature, 350, 1991, pp. 55-57.
Nakakuki T. Yuen D. A. and Honda S., The interaction of plumes with the
transition zone under continents and oceans, Earth Planet. Sci. Lett., 146,
1997, pp. 379-391.
Parmentier E. M. Sotin C. and Travis B. J., Turbulent 3-D thermal
convection in an infinite Prandl number, volumetrically heated fluid;
Implication for mantle dynamics, Geophys. J. Int., 116, 1994, pp. 241-254.
Rykov V. V., Trubitsyn V. P., Computational seismology, v. 26, Geodynamics and
Earthquake Prediction, 1994, p. 94-102 (in Russian).
Rykov V. V., Trubitsyn V. P., Computational seismology, v. 27, Theoretical Problems
of Geodynamics and Seismology, 1994, p. 21-41 (in Russian).
Rykov V. V. and Trubitsyn V. P., Numerical technique for
calculation of three-dimensional mantle convection and tectonics of
continental plates, in Computational Seismology and Geodynamics, v. 3
ed. by D. K. Chowdhury. Am. Geophys. Un., Washington D.C. 1996a. pp. 17-22.
(English translation of Vychisliteljnaya seismologiya,
Nauka, M., No. 26, 1994, pp. 94-102)
Rykov V. V and Trubitsyn V. P., 3-D model of mantle convection
incorporating moving continents, in Computational Seismology and Geodynamics,
v. 3 ed. by D. K. Chowdhury. Am. Geophys. Un., Washington
D.C., 1996b, pp. 23-32.
(English translation of Vychisliteljnaya seismologiya,
Nauka, M., No. 27, 1994, pp. 21-41)
Samarsky A. A., Nikolayev E. C., Methods of Solving Residual Equations, Nauka,
M.,
1978, 591 pp. (in Russian).
Samarskii A. A. and Nikolaev E. S., Method of solving finite-difference equations
(in Russian), Nauka, M., 1978, 591 p.
Solheim L. P. and Peltier W. R., Phase boundary deflections at 660-km depth
and episodically layered isochemical convection in the mantle, J. Geophys. Res.,
99, 1994, pp. 15861-15875.
Tackley P. J., Stevenson D. J., Glatzmaier G. A., Schubert G., Effect of
multiple phase transitions in three dimension spherical model of convection
in Earth's mantle, J. Geophys. Res., 99, 1994, pp. 15877-15901.
Trubitsyn V. P., Belavina Yu. F., Rykov V. V., Physics of the Earth,
N. 11, 1993, p. 3-13 (in Russian).
Trubitsyn V. V., Belavina Yu. F., Rykov V. V., Thermal and mechanical
ineraction of mantle and continental lithosphere, Izvestiya, Physics of the
solid Earth, 29, 1993, pp. 933-945. (English translation of
Fizika Zemli, No. 11, 1993, pp. 3-13. Published by American
Geophysical Union and Geological Society of America).
Trubitsyn V. P., Belavina Yu. F., Rykov V. V., Physics of the Earth,
N. 7/8, 1994, p. 5-17 (in Russian).
Trubitsyn V. V., Belavina Yu. F., Rykov V. V., Thermal mantle convection in
a varying viscosity mantle with a finite-sized continental plate,
Izvestiya, Physics of the solid Earth, 30, 1995, pp. 587-599.
(English translation of Fizika Zemli, No. 7/8, 1994, pp. 5-17. Published
by American Geophysical Union and Geological Society of America).
Trubitsyn V. P., Bobrov A. M., Physics of the Earth,
N. 9, 1993, p. 27-37 (in Russian).
Trubitsyn V. P., Bobrov A. M., Kubyshkin V. V. Physics of the Earth,
N. 5, 1993, p. 3-11 (in Russian).
Trubitsyn V. P., Bobrov A. M., and Kubyshkin V. V., Influence of
continental lithosphere on structure of mantle thermal convection,
Izvestiya, Physics of the solid Earth, 29, 1993, pp. 377-385.
(English translation of Fizika Zemli, No. 9, 1993, pp. 27-37. Published
by American Geophysical Union and Geological Society of America).
Trubitsyn V. P., Bobrov A. M., Computational seismology, v. 27, Theoretical Problems
of Geodynamics and Seismology, 1994, p. 3-20 (in Russian).
Trubitsyn V. P., Bobrov A. M., Computational seismology, v. 28, Modern Problems
of Seismicity and Earth Dynamics, 1996, p. 22-31 (in Russian).
Trubitsyn V. P. and Bobrov A. M., Structure evolution of mantle convection
after breakup of supercontinent, Izvestiya, Physics of the solid
Earth, 29, 1994, pp. 768-778. (English translation of Fizika Zemli,
No. 9, 1993,
pp. 27-37. Published by American Geophysical Union and
Geological Society of America).
Trubitsyn V. P. and Bobrov A. M., Thermal and mechanical interaction of
continents with the mantle, in Computational Seismology and Geodynamics, v.
3, ed. by D. K. Chowdhury. Am. Geophys. Un., Washington
D.C, 1996, pp. 33-41. (English translation of Vychisliteljnaya seismologiya,
Nauka, M., No. 27, 1994, pp. 3-20).
Trubitsyn V. P and A. M. Bobrov A. M., Structure of mantle convection
beneath stationary continents, in Computational Seismology
and Geodynamics, v. 4, ed. by D. K. Chowdhury. Am. Geophys. Un., Washington
D.C., 1997, pp. 42-53. (English translation of Vychisliteljnaya seismologiya,
Nauka, M., No. 28, 1996, pp. 22-31).
Trubitsyn V. P., Fradkov A. C., Physics of the Earth, N. 7, 1985, p. 3-14
(in Russian).
Trubitsyn V. P. and Fradkov A. S., Convection under continnts and oceans, Izvestiya,
Physics of the solid Earth, 21, No. 7, 1985, pp. 491-498.
(English translation of Fizika Zemli, No. 7, 1985, pp. 3-13. Published
by American Geophysical Union and Geological Society of America).
Trubitsyn V. P. and Rykov V. V., A 3-D numerical model of the Wilson
cycle, J. Geodynamics, 20, 1995, pp. 63-75.
Trubitsyn V. P., Rykov V. V., Physics of the Earth,
N. 6, 1997, p. 1-12 (in Russian).
Trubitsyn V. P. and Rykov V. V., Mechanism of formation of an
inclined subduction zone, Izvestiya, Physics of the Solid Earth, 33,
No. 6, 1997, pp. 427-437.
(English translation of Fizika Zemli, No. 6, Interperiodica Publishing,
1997, pp. 1-12).
Turcotte D. L. and Schubert G., Geodynamics: Applications of Continuum Physics
to Geological Problems, John Wiley, New York, 1982, 449 pp.
Zalesak S. T., Fully multidimensional flux-correced transport algorithms for
fluids, J. Comp. Phys., 31, 1979, pp. 335-361.
Zhong S. and Gurnis M., Dynamic feedback between a continentlike raft
and thermal convection, J. Geophys Res., 98, 1993, pp. 12219-12232.
Zhong Sh. and Gurnis M., Role of plates and temperature-dependent
viscosity in phase change dynamics, J. Geophys. Res., 99, 1994, pp.
15,903-15,917.
Load files for print and local use.
This document was generated by TeXWeb
(Win32, v.1.0) on February 23, 1999.
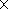 80 mesh, including a thin
continent of thickness
d = 90 km and horizontal size
l = 6000 km. The
long-term evolution of the mantle-continent system is calculated.
Comparison of the evolution of unsteady-state convection in the mantle
with and without a continent shows that the moving continent dramatically
changes the mantle convection structure.
80 mesh, including a thin
continent of thickness
d = 90 km and horizontal size
l = 6000 km. The
long-term evolution of the mantle-continent system is calculated.
Comparison of the evolution of unsteady-state convection in the mantle
with and without a continent shows that the moving continent dramatically
changes the mantle convection structure.
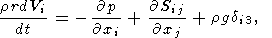
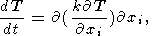
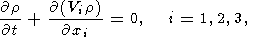
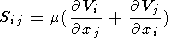
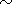 10-23 with respect to the
right-hand terms. Therefore, these
inertial terms may be neglected.
10-23 with respect to the
right-hand terms. Therefore, these
inertial terms may be neglected.
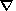 p = -r0g.
Also, we introduce dimensionless variables
taking, as measurements units, the mantle thickness
D for length,
k/D for velocity,
D2/k for time,
T0 for temperature,
m
for viscosity, and
mk/D2 for pressure and
stresses.
p = -r0g.
Also, we introduce dimensionless variables
taking, as measurements units, the mantle thickness
D for length,
k/D for velocity,
D2/k for time,
T0 for temperature,
m
for viscosity, and
mk/D2 for pressure and
stresses.
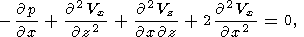
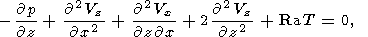
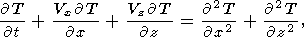
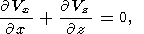
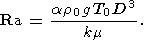
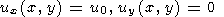
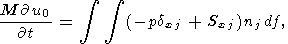
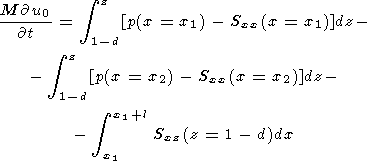
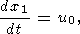
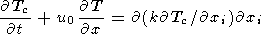
 10-23 compared to the
terms in its right-hand side. Substituting deviator
tensor of viscous stresses (4) into (12) and omitting inertial terms, we
obtain the equations of continent motion in dimensionless variables
10-23 compared to the
terms in its right-hand side. Substituting deviator
tensor of viscous stresses (4) into (12) and omitting inertial terms, we
obtain the equations of continent motion in dimensionless variables
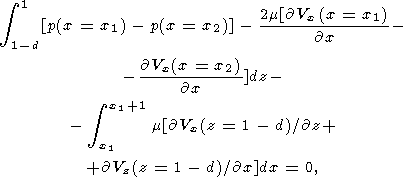
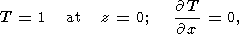
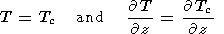
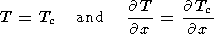
 d ).
d ).
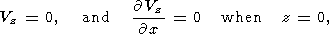

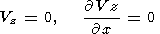
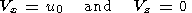
 Vz/
Vz/