RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 19, ES6006, doi:10.2205/2019ES000683, 2019

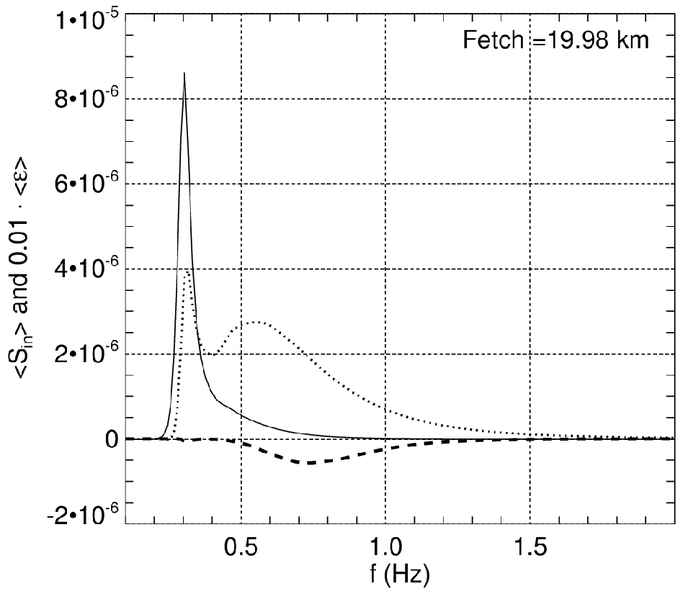
Figure 9. Angular averaged wave energy wind input $ < S_{in} > = \frac{1}{2 \pi} \int \gamma_{in}(\omega,\theta)$ $\varepsilon(\omega,\theta) d\theta$ (dotted line), wave breaking energy absorption $ < S_{diss} > = \frac{1}{2 \pi}\int \gamma_{diss}(\omega,\theta)$ $ \varepsilon(\omega,\theta) d\theta$ (dashed line) and angular averaged spectrum $ <\varepsilon> = \frac{1}{2\pi} \int \varepsilon(\omega,\theta) d\theta$ (solid line) depending on the frequency $f$ (solid line).

 
Citation: Pushkarev Andrei (2019), On different approaches to statistical description of ocean waves, Russ. J. Earth Sci., 19, ES6006, doi:10.2205/2019ES000683.
 

Copyright 2019 by the Geophysical Center RAS.