[55] We studied three types of effects: asymmetric impulses, oscillations periodicity, and noise synchronization in the range of periods from several minutes to tens of minutes from records of seismic stations of the same type in time intervals of the order of 1 month before 4 strong earthquakes.
[56] We show the results in Table 1 with the following symbols: in columns 2-7 I is for asymmetric impulses, P is periodicity, S is synchronization, Iz, Pz and Sz show location of the effect in the seismically active zone, where the earthquake occurred. Symbols (+), (-), (?) indicate appearance, non-appearance of the effect and uncertain result. Note that the table is based on our present knowledge based on limited amount of cases and relatively short time interval and may be improved in the future.
[57] Symbol (+) in columns Iz, Pz, Sz (location of the effect in the seismically active zone) means that the effect was more pronounced at stations that are located nearer to the earthquake epicenter. The uncertainty of results on synchronization before Neftegorskoe earthquake is explained by the fact that gaps in recording that did not coincide in time and lasted several days were left at most stations; interval of 6 days suitable for joint analysis was too short to allow obtaining stable results. For Sumatra earthquake, symbol (?) is used in the columns of location in the seismically active zone, because now the data have not been analyzed that were obtained by stations located at distances considerably exceeding the rupture length (~1000 km) of this gigantic earthquake.
[58] We shall examine the feature of uniqueness of the effect appearance before the earthquake. If the effect appeared only once before the earthquake in the closing length of time interval under investigation, we shall conventionally consider it to be unique. Data having been obtained by the present do not allow us to conclude if the three types of effects mentioned above had the feature of uniqueness. It is established that the effects of oscillations periodicity and noise synchronization may be repeated also after strong remote earthquakes and foreshocks. The possibility is not excluded that they might be repeated owing to trigger effect of tides and meteorological factors. The problem of uniqueness of asymmetric impulses appearance still remains to be solved.
[59] With account for the table we come to the conclusion that the effects under investigation fall in the class of phenomena that are characteristic of non-equilibrium systems dynamics. The causes of their formation may be inside and outside the solid earth. Processes in the outer spheres of the earth (the atmosphere, ionosphere) are characterized by both random and quasi-periodic components. We proceed from the assumption that the dissipative system of seismically active zone is in meta-stable state and processes going on in it have characteristics of determined chaos. Similar systems exist in different areas of the inner and outer spheres of the earth. If microseisms field in minute range of periods reflects space and time variations of different dynamic systems parameters and non-zero coefficients of relation between parameters of these systems exist, then mutual influence made by each system on another may be possible. It is well known that random systems show synchronization effects, especially in the attractors area. [Ott, 2002; Pykovski et al., 2003]. Synchronization of the systems dynamics may appear and be interrupted, and at some time intervals it may be stable [Gauthier and Bienfang, 1996].

|
| Figure 18 |
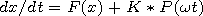 | (10) |
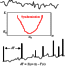
[61] Suppose we deal with oscillations in the lithosphere and coefficient K shows the extent of influence of atmospheric pressure periodic disturbances made on them. Synchronization area in the frequency band w (Figure 18) is characterized by the following important characteristics [Ott, 2002]: it is not manifested if the relation coefficient K is less than threshold K0; it expands as K increases. We can assume that as macro-instability (earthquake) approaches, the sensitivity of the lithosphere meta-stable area (value K ) to the atmosphere pressure effect increases.
[62] In paper [Saltykov et al., 1997] facts were described of phase synchronization formation of high-frequency seismic noise (30 Hz) and tides. In our case, the rise of impulses in minute range of periods did not correlate with either the level of high-frequency microseisms of storm origin or the phases of earth tides. However, synchronization of stations records separated by thousands of kilometers and by tens of degrees in longitude suggests a common source. The rise of synchronization level when selecting stations located nearer to the earthquake epicenter may be associated with two features: the location of synchronization source in the corresponding seismically active zone and tensosensitivity rise of the zone to external effects caused by a remote source as the oncoming disaster approaches.
[63] Rhythms formation is a common phenomenon in non-equilibrium systems evolution [Nicolis and Prigogine, 1989]. It is important in this case that rhythmic oscillations may be of pulse form. Among impulses we revealed, there were symmetric and asymmetric impulses. By symmetry is meant approximately equal amplitude of positive and negative phases of oscillations. Figure 5 and curve 2 in Figure 7 show examples of such impulses. Asymmetric impulses locally appeared as series (Figure 9) and, as the moments of Kronotskoe and Neftegorskoe earthquakes approached, their number increased (Figure 6). Such phenomena are known in the dynamics of random systems. The chart of impulse formation against oscillations of equation (10) type is presented in the lower plot (Figure 18). In paper [Gauthier and Bienfang, 1996] it is shown that with approaching macro instability in the stage of transitional bubbling conditions, synchronization intervals are interrupted by short-time bursts with large amplitude. With the development of macro instability the effect may be noted of bursts frequency increase [Ott, 2002].
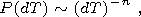 | (11) |
where P(dT) is probability of intervals formation of duration dT between bursts and n>1, that is probability of short interval is higher. It was demonstrated in the studies of a relatively simple dynamic system when a particle placed in viscous liquid was affected by electric field and sinusoidal vibration. The situation inside the earth is much more complex, so this example only suggests that a phenomenon like this is possible in principle.
[64] Here it is worth noting one of the characteristics of impulse oscillations, which was only mentioned in the aforesaid. For the case of Kronotskoe, Neftegorskoe and Hokkaido earthquakes, the system of stations allowed us to compare records by stations located near the sources and by remote stations. For example, in the case of Kronotskoe earthquake, its epicenter was located at the following distances in kilometers from the stations participating in the studies: PET - 350, MAG - 900, YSS - 1670, YAK - 2050, ARU - 5900, and OBN - 6800. If the impulse oscillations were elastic waves, then with duration (period) of T = 10 minutes the wavelength in the conditions of the upper lithosphere, the earth's crust would be from 2000 to 4000 km for surface and longitudinal body waves respectively. Then 2-3 stations closest to the epicenter would be within the wavelength (near zone) and we would expect that one and the same impulse would be recorded at those stations with a shift of several minutes. However attempts to identify clearly the same impulses at neighboring stations have not met with success; coincidence was observed only for strongest ones [Sobolev et al., 2005]. Therefore at the present stage we hold to the idea that the physical nature of the impulses is related to inelastic (quasi plastic) movements in the sources of earthquakes under preparation or fault zones located near them. In Kronotskoe and Hokkaido earthquakes it may have been subduction zone, in Neftegorskoe earthquake it may have been the regional fault extending along Sakhalin from the epicenter to YSS station. We draw attention to the fact that oscillations presented in Figures 5, 7, and 8 have dimensionality of displacement velocity (nM s-1 ). In case of one-polar impulse, they signify seismometer reaction to one step of ground displacement of several-minutes duration. The analogy of creep on the fault suggests itself.

Powered by TeXWeb (Win32, v.2.0).