2. General Equations and Asymptotic Formula for Wave Profile in the Uniform Depth Basin

2.1. The General Equations

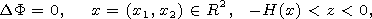
[4]  Let us give first very rough arguments showing the possibility to use (1, 2) for a description of tsunami waves in a frame of the piston model over slow varying bottom. The equations (1) are obtained from the following linear equations of the piston model without the assumption of long wave approximation for the velocity potential F(x,z,t) and the elevation of the free surface h(x,t) (see e.g. [Whitmore and Sokolowski, 1996; Pelinovski, 1996; Kowalik and Murty, 1993; Lewis and Adams, 1983; Shokin et al., 1989; Tinti, 1993])

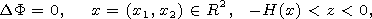(3)

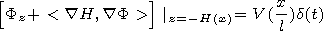where d is the delta function, and it is assumed that F 0, h 0 when t< 0.

[5]  The task is to evaluate h(x,t) at large distances |x|>>l from the source, near the wavefronts (where |h| has its maximum values), assuming that l>>H(x) and that the depth H(x) has a small variation at distances of the order l.

2.2. Asymptotic Formula

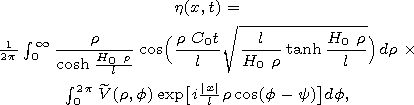(4)

where

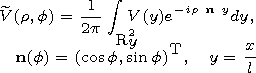(5)

and the angle y is defined by the equations

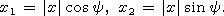Below, we consider in detail the case, when the initial vertical displacement of the bottom is like a ridge (or a valley), though the approach developed here is applicable for any other localized disturbance.

[7]  To make final formulas more explicit let us model the initial displacement using the function of the type of the Gaussian exponent with oscillations:

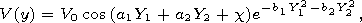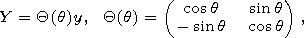(6)

where a₁, a₂, 1 < b₁, b₂ < 3, q, c are dimensionless parameters and V₀ is the parameter of the dimension of length.

[8]  Substituting for V(y) from (6) in (5) we obtain

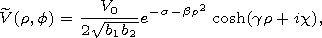(7)

where

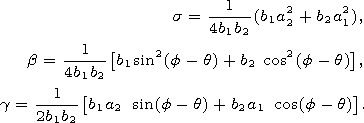(8)

Now we derive the equation (9) under the main assumption |x|>>1. We estimate the integral with respect to q by the stationary phase method. After some calculations we have the following asymptotic formula for h(x,t) (see [Borovikov and Kelbert, 1996; Dobrokhotov et al., 1993; Berry, 2005]):

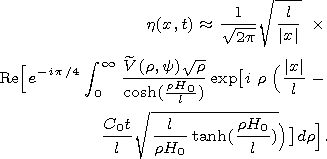(9)

[9]  From (7) and (8) one can conclude, reminding the above assumption on the values of the parameter b, that the main contribution to the integral (9) corresponds to the values of r in the interval 0 < r< 3. Moreover, since |x|/l>>1 integral (9) is not small only in the case when the expression in the big parentheses in the exponent of the integrand is small. Further, since H₀/l<<1, the functions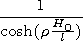 and in the integrand can be expanded in Taylor series in the powers of rH₀ / l:

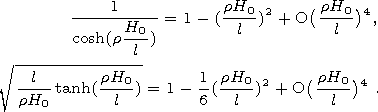(10)

One can see that the integral (9) gets its largest values near the circle |x|=C₀ t, i.e. in a neighborhood of the wavefront. Then, if we take in series (10) the first terms only, we obtain from (9) the formulae for h(x,t) in the long waves approximation. From (9) and (10) we can derive roughly the following requirement for the correctness of the long wave approximation

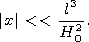(11)

Taking H₀=4 km, l=50 km we find from (11) that for the typical conditions of the ocean, equation (1) can be used instead of the general equations (3) in the piston model in the case of a basin of uniform depth. We note that the same conclusion can be done for initial disturbances of more general types than those described by (6) as well as in the case of a basin with a non-uniform slowly varying depth. According to this reason we will consider here the problem in the long wave approximation (1, 2) instead of the general equations (3).

[10]  Thus, from (9) an asymptotic formula for h(x,t) at any instant t and observation point x located near wavefront and satisfying requirement |x|>>l and (11) becomes

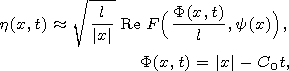(12)

where y is the angle between the vector x and the axis Ox₁,

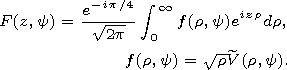(13)

In (13) the function

is given by (5) for an initial disturbance of a general type and by (7) for the disturbance (6) considered here. In the last case the integral in (13) is evaluated analytically and F(z,y) becomes

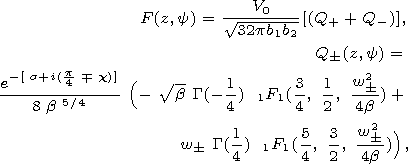(14)

where

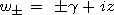and ₁F₁(...) are the Kummer's confluent hypergeometric functions. The function F can be expressed also in terms of parabolic cylinder functions D_<font face="Symbol">n (see [Dobrokhotov et al., 1991]), we use here the form given by Mathematica.

Figure 1

Re F(z,y) on z

Figure 2

is presented in Figures 1 and 2 for different values of the angle  y.

[12]  Figure 1 shows that in the case b₁ 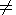b₂ (non axially symmetric initial bottom disturbance) the wave profile has different forms at different values of the angle y, while Figure 2 shows that the difference becomes very strong if a₁ a₂. So the wave profile crucially depend on the form of initial disturbance determined by (6).

[13]  In the case of the initial disturbance of general type, the function F(z,y) can be calculated from (13) and (5) numerically. The calculation is simplified by the fact that the important part of the integral (13) corresponds to the values of the variable of integration r of the order of several units.

[14]  Keeping in mind that the structures of the asymptotic formulae for h(x,t) are similar in the cases of the basins of uniform and non uniform depth (see Sec 3), we give the following comments on the formulae (12) using terminology of the WKB theory.

[15]  The function F(x,t) in (12) can be called the phase because of two facts. First, from (12) and (13) it is clear that |h(x,t)| has a maximum when F(x,t)=0 and decays rapidly with increasing |F(x,t)|. Second, outside of the neighborhood of origin x=0 the function F(x,t) is the action or a solution of 2-D Hamilton-Jacobi equation

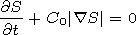(15)

corresponding to (1) in the case of the basin of the uniform depth H₀.

[16]  The integration of the last equation is connected with the Hamiltonian system (see e.g. [Maslov and Fedoiuk, 1981]); for (15) it is determined by the following 2-D Hamiltonian H=C₀|p|, where p=(p₁,p₂) is a momentum. Thus the corresponding Hamiltonian system has the form

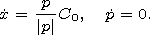(16)

Consider the one-parametric family of trajectories of this system satisfying the following initial conditions

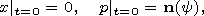(17)

where

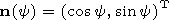(18)

and the angle y [0,2p] is a parameter. These trajectories are (vector-columns) X(t,y)=(C₀ t cos y, C₀ t sin y)^T, P(t,y)= n(y). The family of trajectories X(t, y), P(t,y) go out from the point x=0 with a unit momentum p= n(y). The projection of the trajectory x=X(t, y) on the plane is called "ray". Here the rays are the straight lines starting from the point x=0 and arriving at the instant t to the point x₁=C₀ t cos y, x₂=C₀ t sin y. At every instant t>0 the curve formed by the end of the rays is called the "wavefront". Here the wavefronts are the circles |x|=C₀ t. One can see from (12) that at the wavefronts the phase F=0. It should be noted also that the points on the front are parameterized by the parameter y (0,2p] which was introduced in (17) as the initial condition for the impulse p(t). So, y in (12) can be considered with the same point of view.

[17]  In the case of a basin with a non-uniform depth, asymptotic formulas for h(x,t) have a structure similar to that in (12). But the rays are no more straight lines, the Hamiltonian is more complicated, the factor (l / |x|)^1/2 has to be replaced by other one and sometimes the power in the exponent e^-ip/4 has to be multiplied by an integer number m which has a deep topological meaning since it is possible, under certain condition, to evaluate m as the Morse index of the trajectory.

[18]  Anyway, it is clear that the algorithm for calculating h(x,t) from the (12) is faster than the finite difference method since for finding the value of the amplitude of the tsunami front passing in the point x at time t it is not necessary to integrate over all the space but one need just to identify the trajectory starting from the point where the initial perturbation has taken place and arriving to the point x at time t. In other words this method of integration is "local" in the sense that it is concentrated on the trajectories of an Hamiltonian system. This Hamiltonian system is not difficult to solve numerically in the case of a basin of non-uniform depth.

---

---

Powered by TeXWeb (Win32, v.2.0).