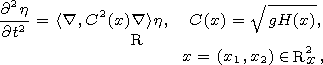
[2] The traditional modelling of the tsunami waves propagation in the open ocean is done by solving the linear hydrodynamical equation in 2-D long wave approximation and in the framework of the so called "piston model'', which assumes that the source of the tsunami is given by an instantaneous vertical velocity of a certain region of the bottom of the ocean which generates an uplift of the ocean surface
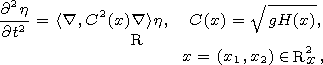| (1) |
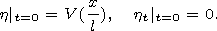 | (2) |
Here
h(x,t) is the elevation of the ocean surface,
H(x) is the depth of the basin,
g is the gravity acceleration, and
V(x/l) is the uplift of the ocean surface localized in the area
of a characteristic size
l. It is assumed that
l is small
in comparison both with the characteristic length of the
interval of change of the bottom depth and the distance from the
observation point. This means in particular also that the
function
V(y) decays fast as
|y|
. Usually the
problem (1, 2) is solved numerically with
finite difference methods. However analytical formulas of
solutions are useful from different points of view. The main
reason is that it is not so easy to use direct numerical
methods for real time tsunami warning, because they take too
much time and require too much information on the tsunami sea
bottom source.
[3] Problem (1, 2) seems like a classical one for mathematical physics and asymptotical analysis. Nevertheless the explicit formula for its solution (which can be transformed in a computer program for fast calculation of wave profiles) were obtained quite recently, although some asymptotic representation was given in [Dobrokhotov et al., 1991]. The main mathematical difficulties here are related with the metamorphosis of the solution: it is localized in the neighborhood of the point x=0 (the origin) at t=0, but after some time it changes its structure taking the form of a function localized in the neighborhood of a closed curve (the wave front), which in turn can have sometimes self-intersection and singular (focal) points. This phenomena was described in asymptotic theories for fast oscillating and non smooth solutions of a wide range of partial differential equations. The global representation for fast oscillating solutions (with effects of focalization taken into account) is given by the Maslov canonical operator [Maslov, 1965; Dobrokhotov and Zhevandrov, 2003]. However, one cannot apply this theory to problem (1, 2) directly because the solutions in this case have a different structure. Nevertheless two simple ideas allow one to modify the Maslov approach and obtain explicit asymptotic formulas for the solutions of (1, 2): 1) the problem about localized solutions can be transformed to the one about fast oscillating solutions with a Fourier-type integral transform, 2) the final formulas can be simplified if one takes into account the ideas from boundary layer expansions near the wave fronts. We combine these ideas together with the Maslov theory [Maslov, 1965; Maslov and Fedoiuk, 1981; Dobrokhotov and Zhevandrov, 2003] and results from [Dobrokhotov et al., 1991; Maslov and Fedoiuk, 1989]. Finally we propose an asymptotic-numerical description of tsunami in a basin with non-uniform depth in a neighborhood of wavefronts that can have caustics. This approach takes into account in a simple and direct way physical effects (like the metamorphosis of the tsunami front mentioned above) coming from the singularities related with the Hamiltonian system i.e. focal points and caustics. The presented formulas can be transformed in a computer program by means of the software of the type of Mathematica or Maple for calculating wave profiles and so they can be used for a reliable early warning system. Here we explain the meaning of the final formulas announced by Dobrokhotov et al., [ 2006a] (some more details can be found in [Dobrokhotov et al., 2006b]). In the graphics we show that many features of the tsunami wave propagation in such basins can be explained by means of straightforward formulas without any additional complications.
Powered by TeXWeb (Win32, v.2.0).