Discussion and Conclusion
[19] One of the most noticeable features of the
inferred structures is anomalously low velocities
in the upper crust. Thus,
Vp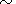 4.1 km s
-1 and
Vs
4.1 km s
-1 and
Vs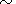 2.4 km s
-1 in the uppermost layer about 1 km
thick. Figure 4 shows the results of the average
receiver function inversion from data of 12
earthquakes recorded at the stations C1, C3, and
C5. If the receiver function is inverted from the
data of the station C5 alone (Figure 2), the
inverted velocities in the upper layer are even
lower:
Vp = 3.5 km s-1 and
Vs = 2 km s-1.
Apparently, these are the lowest velocities that
have ever been observed in the upper crust of the
Karelia region. In any case, such low velocities
are absent in the velocity structures presented in
[Sharov, 2004].
The velocity
Vp
2.4 km s
-1 in the uppermost layer about 1 km
thick. Figure 4 shows the results of the average
receiver function inversion from data of 12
earthquakes recorded at the stations C1, C3, and
C5. If the receiver function is inverted from the
data of the station C5 alone (Figure 2), the
inverted velocities in the upper layer are even
lower:
Vp = 3.5 km s-1 and
Vs = 2 km s-1.
Apparently, these are the lowest velocities that
have ever been observed in the upper crust of the
Karelia region. In any case, such low velocities
are absent in the velocity structures presented in
[Sharov, 2004].
The velocity
Vp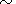 5.5 km s-1 is attained at a depth of about 3 km, and
Vp
5.5 km s-1 is attained at a depth of about 3 km, and
Vp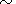 6.2 km s-1, only at a depth of about 10 km.
Low velocities in the upper hundred meters are not
surprising. All RUKSA stations were mounted on
moraine deposits. However, anomalously low
velocities are sometimes also observed in
bedrocks of the upper crust
[Vinnik et al., 2002].
Grad and Luosto [1992]
reported relatively low velocities in the upper crust
from the SVEKA profile in Finland. The velocities were
determined from observations of short-period
(0.5-2.5 Hz) Rayleigh waves. The lowest surface
wave velocity is 2.7 km s-1, which yields an
S wave velocity of 2.9 km s-1. Based on the analysis of
O'Connel and Budiansky, 1977],
Grad and Luosto attributed the relatively low velocities to
the fracturing of upper crust rocks provided that the
cracks are isolated and filled with water. Our
observations yield much lower velocities that can
also be accounted for by the presence of cracks
filled with water except that all or some part of
the cracks are interconnected. According to the
calculations of O'Connel and Budiansky, an
S wave velocity decrease in the case of isolated
cracks reaches 25% compared to a monolithic
rock. The concentration of cracks was assumed to
be 0.5. If the cracks are not isolated, the
velocity decrease is 60%. In our case, the
observed
S velocities amount to
6.2 km s-1, only at a depth of about 10 km.
Low velocities in the upper hundred meters are not
surprising. All RUKSA stations were mounted on
moraine deposits. However, anomalously low
velocities are sometimes also observed in
bedrocks of the upper crust
[Vinnik et al., 2002].
Grad and Luosto [1992]
reported relatively low velocities in the upper crust
from the SVEKA profile in Finland. The velocities were
determined from observations of short-period
(0.5-2.5 Hz) Rayleigh waves. The lowest surface
wave velocity is 2.7 km s-1, which yields an
S wave velocity of 2.9 km s-1. Based on the analysis of
O'Connel and Budiansky, 1977],
Grad and Luosto attributed the relatively low velocities to
the fracturing of upper crust rocks provided that the
cracks are isolated and filled with water. Our
observations yield much lower velocities that can
also be accounted for by the presence of cracks
filled with water except that all or some part of
the cracks are interconnected. According to the
calculations of O'Connel and Budiansky, an
S wave velocity decrease in the case of isolated
cracks reaches 25% compared to a monolithic
rock. The concentration of cracks was assumed to
be 0.5. If the cracks are not isolated, the
velocity decrease is 60%. In our case, the
observed
S velocities amount to
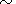 2.4 km s-1,
whereas a value of 3.6 km s-1 is expected for rocks
of the granite type. The velocity decrease
amounts to 40% and, as distinct from the SVEKA
profile observations, can accounted for by
partially interconnected cracks. This inference
could be supported (or disproved) by estimating
the crack density from measurements of the number
and sizes of fractures in the RUKSA area.
Vinnik et al. [2002]
noted a 30% decrease in
S velocities at some points of
the upper crystalline crust in central Tien Shan and
interpreted this decrease in terms of the
fracturing in the shallow layer. Our data are
insufficient to assess to what extent the
velocity decrease is affected by moraine
deposits, the isolation or interconnectedness of
cracks, and the possible presence of particularly
low velocity rocks in the volcanogenic sedimentary series.
All three factors appear to be significant.
2.4 km s-1,
whereas a value of 3.6 km s-1 is expected for rocks
of the granite type. The velocity decrease
amounts to 40% and, as distinct from the SVEKA
profile observations, can accounted for by
partially interconnected cracks. This inference
could be supported (or disproved) by estimating
the crack density from measurements of the number
and sizes of fractures in the RUKSA area.
Vinnik et al. [2002]
noted a 30% decrease in
S velocities at some points of
the upper crystalline crust in central Tien Shan and
interpreted this decrease in terms of the
fracturing in the shallow layer. Our data are
insufficient to assess to what extent the
velocity decrease is affected by moraine
deposits, the isolation or interconnectedness of
cracks, and the possible presence of particularly
low velocity rocks in the volcanogenic sedimentary series.
All three factors appear to be significant.
[20] In the lower and upper crust, at depths of 10 km to 40 km,
the
P wave velocity slowly rises to about 6.6 km s-1.
Its average gradient at these depths is an order of magnitude
smaller than in the upper crust at depths of 0 km to 10 km.
The Moho depth is about 40 km. The
P velocity immediately
under the Moho is 8.4 km s-1. This value is much higher than
in the IASP91 model but is consistent with modern models
of ancient shields. Thus, the velocity structure obtained
in this work consists of an essentially heterogeneous
upper part where the velocity (converted into
P wave
velocity values) rises from 3.5 km s-1 at the surface
to 6.2 km s-1 at depths of 10-12 km and nearly homogeneous
middle and lower parts with minimal velocity contrasts
in the corresponding layers. Velocity inversion zones are
virtually absent in the final variant of the velocity structure.
[21] Previously we presented and discussed the
velocity structure beneath RUKSA obtained from a
receiver function alone, without invoking data on
surface waves and traveltimes of converted waves
from the 410-km boundary
[Sharov, 2004].
The main features of the structure, the Moho depth and
average velocities in the crust and the mantle,
are close to those inferred in our study.
Distinctions are mainly observed in the upper
part of the section and can be attributed to the
instability of the inversion using data of the
receiver function alone. The extent of misfit
(the rms deviation) between the synthetic and
observed waveforms of the published structure is
1.5 times greater than in our present work.
[22] Reliable features of the presented models (Figure 4)
are the presence of a sharp boundary at a
depth of about 40 km (the Moho), anomalously low
velocities in the depth interval 0-3 km that are
untypical of ancient shields, a rapid rise in the
velocity with depth in the upper crust, and weak
differentiation in velocities of the middle and
lower crust. Significant heterogeneities in the
upper part of the crystalline crust to depths of
12-15 km were previously noted in studies of the
fine structure of seismic wavefields from small
aperture array data
[Nevsky and Riznichenko, 1980].
[23] Thus, using data of short-period instrumentation
with improved characteristics, a detailed
velocity structure is obtained beneath the RUKSA
small aperture array. These data are necessary
for remote location of seismic events. They can
also be used for the construction of a 3-D
lithosphere model of the European part of the
Russian Federation. This approach is promising if
mobile small-aperture arrays and natural sources
(remote earthquakes) are used for local mapping
of crustal boundaries from seismic data of
relatively short period instrumentation.

Powered by TeXWeb (Win32, v.2.0).
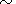 4.1 km s
-1 and
Vs
4.1 km s
-1 and
Vs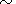 2.4 km s
-1 in the uppermost layer about 1 km
thick. Figure 4 shows the results of the average
receiver function inversion from data of 12
earthquakes recorded at the stations C1, C3, and
C5. If the receiver function is inverted from the
data of the station C5 alone (Figure 2), the
inverted velocities in the upper layer are even
lower:
Vp = 3.5 km s-1 and
Vs = 2 km s-1.
Apparently, these are the lowest velocities that
have ever been observed in the upper crust of the
Karelia region. In any case, such low velocities
are absent in the velocity structures presented in
[Sharov, 2004].
The velocity
Vp
2.4 km s
-1 in the uppermost layer about 1 km
thick. Figure 4 shows the results of the average
receiver function inversion from data of 12
earthquakes recorded at the stations C1, C3, and
C5. If the receiver function is inverted from the
data of the station C5 alone (Figure 2), the
inverted velocities in the upper layer are even
lower:
Vp = 3.5 km s-1 and
Vs = 2 km s-1.
Apparently, these are the lowest velocities that
have ever been observed in the upper crust of the
Karelia region. In any case, such low velocities
are absent in the velocity structures presented in
[Sharov, 2004].
The velocity
Vp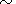 5.5 km s-1 is attained at a depth of about 3 km, and
Vp
5.5 km s-1 is attained at a depth of about 3 km, and
Vp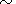 6.2 km s-1, only at a depth of about 10 km.
Low velocities in the upper hundred meters are not
surprising. All RUKSA stations were mounted on
moraine deposits. However, anomalously low
velocities are sometimes also observed in
bedrocks of the upper crust
[Vinnik et al., 2002].
Grad and Luosto [1992]
reported relatively low velocities in the upper crust
from the SVEKA profile in Finland. The velocities were
determined from observations of short-period
(0.5-2.5 Hz) Rayleigh waves. The lowest surface
wave velocity is 2.7 km s-1, which yields an
S wave velocity of 2.9 km s-1. Based on the analysis of
O'Connel and Budiansky, 1977],
Grad and Luosto attributed the relatively low velocities to
the fracturing of upper crust rocks provided that the
cracks are isolated and filled with water. Our
observations yield much lower velocities that can
also be accounted for by the presence of cracks
filled with water except that all or some part of
the cracks are interconnected. According to the
calculations of O'Connel and Budiansky, an
S wave velocity decrease in the case of isolated
cracks reaches 25% compared to a monolithic
rock. The concentration of cracks was assumed to
be 0.5. If the cracks are not isolated, the
velocity decrease is 60%. In our case, the
observed
S velocities amount to
6.2 km s-1, only at a depth of about 10 km.
Low velocities in the upper hundred meters are not
surprising. All RUKSA stations were mounted on
moraine deposits. However, anomalously low
velocities are sometimes also observed in
bedrocks of the upper crust
[Vinnik et al., 2002].
Grad and Luosto [1992]
reported relatively low velocities in the upper crust
from the SVEKA profile in Finland. The velocities were
determined from observations of short-period
(0.5-2.5 Hz) Rayleigh waves. The lowest surface
wave velocity is 2.7 km s-1, which yields an
S wave velocity of 2.9 km s-1. Based on the analysis of
O'Connel and Budiansky, 1977],
Grad and Luosto attributed the relatively low velocities to
the fracturing of upper crust rocks provided that the
cracks are isolated and filled with water. Our
observations yield much lower velocities that can
also be accounted for by the presence of cracks
filled with water except that all or some part of
the cracks are interconnected. According to the
calculations of O'Connel and Budiansky, an
S wave velocity decrease in the case of isolated
cracks reaches 25% compared to a monolithic
rock. The concentration of cracks was assumed to
be 0.5. If the cracks are not isolated, the
velocity decrease is 60%. In our case, the
observed
S velocities amount to
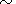 2.4 km s-1,
whereas a value of 3.6 km s-1 is expected for rocks
of the granite type. The velocity decrease
amounts to 40% and, as distinct from the SVEKA
profile observations, can accounted for by
partially interconnected cracks. This inference
could be supported (or disproved) by estimating
the crack density from measurements of the number
and sizes of fractures in the RUKSA area.
Vinnik et al. [2002]
noted a 30% decrease in
S velocities at some points of
the upper crystalline crust in central Tien Shan and
interpreted this decrease in terms of the
fracturing in the shallow layer. Our data are
insufficient to assess to what extent the
velocity decrease is affected by moraine
deposits, the isolation or interconnectedness of
cracks, and the possible presence of particularly
low velocity rocks in the volcanogenic sedimentary series.
All three factors appear to be significant.
2.4 km s-1,
whereas a value of 3.6 km s-1 is expected for rocks
of the granite type. The velocity decrease
amounts to 40% and, as distinct from the SVEKA
profile observations, can accounted for by
partially interconnected cracks. This inference
could be supported (or disproved) by estimating
the crack density from measurements of the number
and sizes of fractures in the RUKSA area.
Vinnik et al. [2002]
noted a 30% decrease in
S velocities at some points of
the upper crystalline crust in central Tien Shan and
interpreted this decrease in terms of the
fracturing in the shallow layer. Our data are
insufficient to assess to what extent the
velocity decrease is affected by moraine
deposits, the isolation or interconnectedness of
cracks, and the possible presence of particularly
low velocity rocks in the volcanogenic sedimentary series.
All three factors appear to be significant.