

|
| Figure 2 |

|
| Figure 3 |
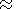 B/H max at
F
B/H max at
F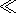 1.
1.
[39] Comparing
Rt and
Rc, it is easy to show that, with increasing
Hc max,
the parameter
Rc reaches an ultimate value at greater values of
B than the
parameter
Rt does. This is due to the fact that the chemical and
thermoremanent magnetizations are mainly due to, respectively, low- and high-
coercivity grains. Note also that, in the experimentally observed range of
interaction fields ( B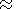 3-30 Oe)
[Ivanov et al., 1981;
Ivanov and Sholpo, 1982],
the maximum value of
Rc is
Rc
3-30 Oe)
[Ivanov et al., 1981;
Ivanov and Sholpo, 1982],
the maximum value of
Rc is
Rc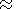 1, whereas
Rt depends on coercivity.
1, whereas
Rt depends on coercivity.
[40] Knowing the response of each particle to an external effect (variations in Hc and Is and the corresponding displacements of representative points in a diagram), we can easily calculate all of the aforementioned types of remanent magnetization and establish the relations between them.
[41] The function g(|H|) can also be applied for the estimation of detrital magnetization in a system of large particles whose orientation is modified by a magnetic interaction field rather than temperature. This estimate is directly related to the so-called cluster model of depositional magnetization developed in [Shashkanov et al., 1989, 2003].
[42] Using the distribution density given by (4), one can show [Belokon and Nefedev, 2001] that, before the decrease in the tilt angle of a certain portion P of elongated or flattened particles, the detrital magnetization is given by the formula
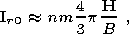 | (26) |
where
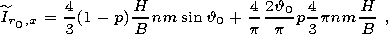 | (27) |
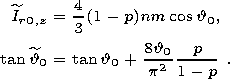 | (28) |
Here
(p2- 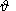 0) is the inclination of
Ir0 and
0) is the inclination of
Ir0 and
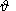 0-
0-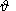 0 is its error.
0 is its error.
[43] In conclusion, we can note the following.
[44] (1) Knowledge of values of Rt and Rc is insufficient for the identification of thermoremanent and chemical magnetizations in an ensemble of single-domain particles. This identification requires additional information on the coercivity and the intensity of magnetostatic grain interaction that can be obtained from laboratory experiments.
[45] (2) Spontaneous magnetization can change with time due to diffusion processes [Afremov and Belokon, 1972]. This can lead to stabilization of the vector Is and a rise in the magnetic moment of the system (diffusion-induced viscous magnetization).
[46] (3) The formation of chemical magnetization can be interpreted in terms of a mechanism [Belokon et al., 1995] that is an analogue of the thermoremanent magnetization formation mechanism and differs from the crystallization mechanism proposed by Haig [1962].

Powered by TeXWeb (Win32, v.2.0).