Magnetic properties of single-domain particles and the rock remanence

3. Magnetic States of Single-Domain Grains

3.1. Chemically Homogeneous Single-Domain Grains

[15] The magnetic state stability is largely controlled by factors unrelated to the external field and giving rise to various anisotropy effects. Along with the natural crystalline form anisotropy, the stress, diffusion, exchange, surface, and other types of anisotropy that are comparable in value with the natural anisotropy can be present in a real ferromagnetic material.

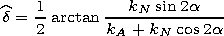
[16] Below, as an example, we address a uniaxial homogeneously magnetized grain having the shape of an ellipsoid of revolution and neglect all types of anisotropy except the natural crystalline and form anisotropies.

[17] In this case, as was shown in [Afremov and Belokon, 1976, 1977], if the dimensionless constants of crystalline and form anisotropy are positive ( k_A > 0 and k_N > 0, respectively), the magnetic moment of a grain is oriented along the effective axis of anisotropy, making the angle

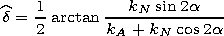(7)

with the axis of the crystalline anisotropy, and its orientation in the equilibrium state can be either parallel or antiparallel to the chosen direction. The critical field H₀ of the transition of one equilibrium state into another is determined by the effective constant of anisotropy K:

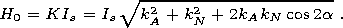(8)

[18] This result is remarkable because it indicates the presence of a spectrum of critical fields in a system of particles differing in k_N and a. Moreover, of the entire set of particles with fixed angle a, particles meeting the condition k_N = -k_A cos 2a possess the weakest critical field H₀ = k_A I_s sin 2a.

[19] Analysis of equilibrium magnetic moment states in grains with k_A 0, k_N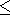 0 and k_A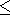 0, k_N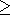 0 [Afremov and Belokon, 1979] shows that equilibrium orientations of the magnetic moment are determined (??) in these cases in the same way as at k_A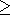 0, k_N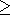 0 whereas, in a magnetic field directed along such an effective easy axis, an irreversible change in the magnetic moment takes place upon reaching the critical field

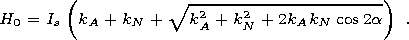(9)

[20] With k_A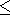 0, k_N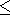 0, the effective easy axis coincides with the intersection of "easy" planes specified by the anisotropy of form and the natural crystalline anisotropy. The orientation of the grain magnetic moment changes irreversibly upon reaching the critical field [Afremov and Belokon, 1979]

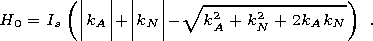(10)

The study of nonspherical particles under uniaxial compression [Afremov and Belokon, 1980a, 1980b] showed that the magnetic moment of a grain is oriented along an effective axis whose position and the effective constant of anisotropy are determined by anisotropy of the crystalline, form and stress types. If the external field is applied along the effective axis and makes an angle b with the axis of the crystalline anisotropy, the position of the effective axis and the critical field of the grain magnetic moment remagnetization depend on the above types of anisotropy as follows:

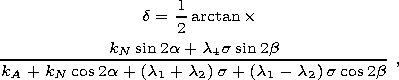(11)

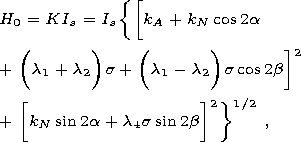(12)

where l_i are magnetostriction constants of a uniaxial crystal and s denotes uniaxial stresses. If the stresses are perpendicular to the plane ( k_A, k_N ), we have

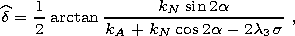(13)

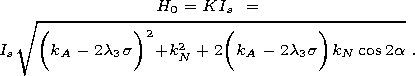(14)

As in the case of two types of anisotropy, the critical field can behave nonmonotonically with variations in the applied stresses. With the stresses oriented parallel to the plane ( k_A, k_N ), the critical field reaches the minimum value H_{0 min} = k_AI_s sin(2a - y₀) at

[k_A + (l₁ + l₂)s + (l₁ - l₂) s cos 2b ]² + l₄s sin 2b]²

= - k_N cos(2a - y₀),

where

If the stresses are perpendicular to the plane ( k_A, k_N ), the critical field attains the minimum value H₀ = k_NI_s sin 2a at k_A-2l₃s = -k_N cos 2a.

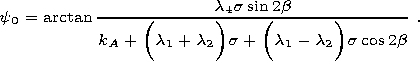[21] Summarizing, we can note the following.

[22] (1) The grain elongation and uniaxial stresses can change significantly the magnetic state of a particle.

[23] (2) The orientation of the effective easy axis and the critical field of an irreversible change in the magnetic moment of a grain are basically dependent on the mutual orientations of the uniaxial stresses and the axes of the crystalline and form anisotropies, as well as on the signs of s, k_A and k_N.

[24] (3) The application of any external force in the absence of a magnetic field can lead to the destruction of remanent magnetization.

Figure 1

3.2. Magnetic States of Two-Phase Particles

[25] It is known that chemical processes (such as oxidation or decomposition of a solid solution) in a magnetically ordered grain can lead to the formation of phases of different compositions and, as a result, an inhomogeneous distribution of magnetic moments. The simplest model of coexisting phases of different compositions is a particle consisting of two crystallographically uniaxial, homogeneously magnetized ferromagnetic phases and represented by a parallelepiped of a base a² and a height qa (Figure 1). Ferromagnetic regions (phases) are characterized by the following parameters: I_s1 and I_s2, spontaneous magnetizations; k₁ and k₂, dimensionless constants of crystalline anisotropy; and 1- e and e, relative volumes of the first and second phases, respectively. For simplicity, we assume that the vectors I_s1 and I_s2 lie in the plane x0z and the crystalline anisotropy axes of both ferromagnetic phases are parallel to the 0z axis. The particle is in an external magnetic field H directed along the 0z axis.

[26] In our analysis, we neglect the magnetoelastic interphase interaction, which can be more or less valid only in the case of a strongly disordered distribution of magnetic atoms in the boundary layer.

3.2.1. Equilibrium grain states in an external magnetic field.

Analysis of the free energy of a grain [Afremov and Belokon, 1996a, 1996b] shows that, in the accepted approximation (in the absence of an external magnetic field), a two-phase particle can exist in one of the following states:

[27] first ( ) state: the magnetic moments of both phases are parallel and directed along the 0z axis;

[28] second ( ) state: the magnetizations of the phases are antiparallel, with the magnetic moment of the first phase m₁ being directed along the 0z axis;

[29] third ( ) state: the magnetic moments of the phases are parallel and opposite in direction to the 0z axis; and

[30] fourth ( ) state: the magnetic moments of the phases are antiparallel, with the first phase being magnetized in the direction opposite to the 0z axis.

[31] If the magnetostatic interaction between the phases prevails over the exchange interaction, N₂₁ = N₂₁-A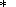 > 0 ( N_ik are the demagnetizing coefficients, A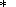 = 2A_in/da I_s1I_s2, A_in is the exchange constant, and d is the width of the interphase transition zone having the same order of magnitude as the lattice parameter), then the first and third states are metastable because the free energy of the grain F = N₂₁I_s1I_s2 in these states is higher than the free energy in the second and fourth states F = -N₂₁I_s1I_s2. The second and fourth states are metastable if N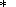₂₁ < 0.

3.2.2. Equilibrium states of a grain in an external magnetic field.

The transitions, for example, from the third to the second or the fourth states are associated with a rotation of the magnetic moment of one of the phases, and the transition fro the third to the first states is associated with a rotation of the total moment of a grain.

[32] Analysis of the grain free energy shows that the third-to-second state transition occurs in the field [Afremov and Panov, 1996a, 1996b]

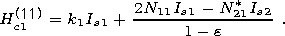(15)

Similar calculations yield the following critical fields:

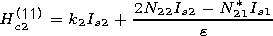(16)

for the third-to-fourth state transition,

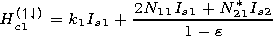(17)

for the fourth-to-first state transition,

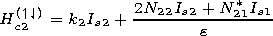(18)

for the second-to-first state transition,

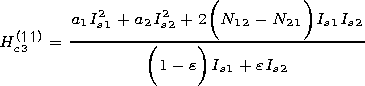(19)

for the third-to-first state transition, and

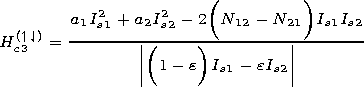(20)

for the second-to-fourth state transition.

3.2.3. The temperature effect on magnetic states of heterogeneous particles.

[33] The above approach is applicable only to the study of magnetic states at T = 0. If T 0, the role of thermal fluctuations increases with decreasing size of particles, and an ensemble of ferromagnetic particles becomes superparamagnetic: its behavior is similar to that of a paramagnetic gas. A distinction is that, depending on the height of the potential barrier between equilibrium states, the magnetic moment of a particle can exist for a certain time t in one of the states.

[34] Because of the small volume of particles, one may expect that, due to thermal fluctuations of magnetic moments of phases, transitions from one equilibrium state into another can be realized in a field H that is smaller than any of the critical fields (15)-(20).

[35] The reorientation of the magnetic moment of a phase is determined by the height of the potential barrier E_ik separating the i th and k th states. The frequency of the i-k state transition is expressed as

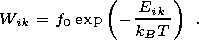(21)

Here f₀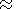 approx 10⁷-10¹⁰ s ^-1 is the characteristic frequency of "attempts" to overcome the potential barrier, k_B is the Boltzmann constant, and E_ik = F_{ik max} - F_{ik min} where F_{ik min} is the free energy of the i th equilibrium state characterizing the particle before the transition and F_{ik max} is the maximum free energy separating the i th and k th states.

[36] If the transition probability from one state to another is known, four equations of "motion" can be constructed for the vector of states:

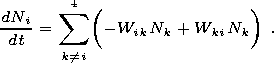(22)

Considering the normalization condition N₁+N₂+N₃+N₄ = 1, these equations can be reduced to the form

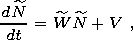(23)

where

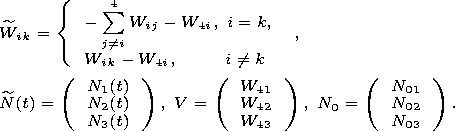(24)

The solution of (23) can be conveniently represented with the use of a matrix exponential:

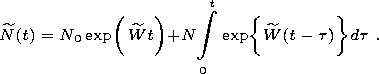(25)

With the known vector of the initial state

n₀ = {N₀₁, N₀₂, N₀₃, N₀₄},

relations (15)-(25) completely determine not only the magnetic state population but also the magnetization of the ensemble of two-phase particles [Afremov and Panov, 1998a, 1998b].