Magnetic properties of single-domain particles and the rock remanence

2. Interaction Between Particles, Phase Transitions, and Spontaneous Magnetization

[4] The interaction between particles randomly scattered in the grain volume or between grains randomly distributed in a nonmagnetic matrix can be conveniently analyzed in terms of the distribution function of random fields used for the first time by Chandrasekhar [1943] (see also [Shcherbakov, 1979]). Such a function was calculated in [Belokon and Semkin, 1992, 1993] with reference to the spin exchange interaction in a lattice with impurity atoms or vacancies. The following three results obtained in these studies are significant for the description of magnetic properties of rock grains, whose lattice is strongly imperfect.

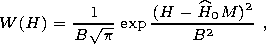
[5] (i) There exists a minimum concentration n₀ of interacting particles (a percolation limit) enabling the formation of spontaneous magnetization.

[6] (ii) The spontaneous magnetization and the Curie point depend on n (at n>n₀ ) and tend toward ultimate values of a "pure" ferromagnetic material.

[7] (iii) Active diffusion of particles should apparently lead to a local increase in the concentration to limits n > n₀, because the concentration phase transition is absent if diffusion is taken into account.

[8] These considerations imply that the Curie point T_c should change (rise) with an increase in the local concentration of (for example, during chemical reactions) and a chemical magnetization should form, as the Curie point rises from T_c < T to T_c > T [Belokon et al., 1995], where T is the temperature during which the reaction proceeds. A more general approximate approach to the estimation of the distribution function of random interaction fields is formulated in [Belokon and Nefedev, 2001, 2002], where the following conclusions were drawn.

[9] (a) The distribution density of random interaction fields has the form of a normal distribution:

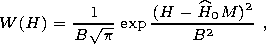(1)

where

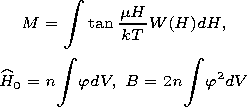(2)

n is the number of interacting particles in a unit volume, and j( r) is the interaction law.

[10] (b) The replacement of the exact distribution function ( 1/p^1/2)exp^-x² by a steplike function of the form

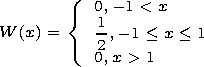(3)

leads to insignificant errors in calculations of mean values.

[11] (c) The system can experience phase transitions to either the spin glass state or the ferromagnetic state, depending on the concentration n and the interaction intensity. In particular, grains and their associations depleted in ferromagnetic atoms can have an ordering of the spin glass type, which is very important in studying viscous processes. If the projection H of the dipole-dipole interaction field in a system of single-domain grains is taken as the function j( r), we obtain the distribution function

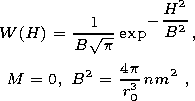(4)

where r₀ is the characteristic sizes of grains and m is the magnetic moment of a grain.

[12] However, we should note that the distribution function of the interaction field modulus |H| should be known in order to calculate the field a and b [Belokon, 1985]:

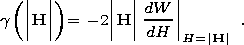(5)

[13] With a known function of distribution of particles over critical fields f(H_c), the density of particles in the Preisach-Neel diagram can be found:

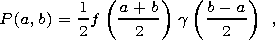(6)

enabling the calculation of any type of remanence [Belokon, 1985].

[14] Other properties of the behavior of single-domain particles related to their significant heterogeneity and the possible concurrent types of magnetic anisotropy are discussed below.