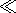 r0,
dr = dr th + dr ch + dr ph
r0,
dr = dr th + dr ch + dr ph V. D. Kotelkin
Mechanical-Mathematical Faculty of the Moscow State University
L. I. Lobkovsky
P. P. Shirshov Institute of Oceanology, RAS
Our approach [Lobkovsky and Kotelkin, 2004] is a synthesizing development of the well-known investigations of mantle convection. These are studies in which:
A new feature of our studies is the analysis of evolution of the mantle layer developing immediately from the post-accretionary state. This approach differs from many previous investigations in which the long-lasting initial stage of computations accounting for the relaxation of initial conditions was ignored due to an unrealistic formulation of the latter and convection regimes were either stationary or oscillating relative to a stationary state. Such convection patterns are undoubtedly important for the understanding of the convection process, and their analysis and systematization have not lost their significance.
However, modern computer technologies enable more sophisticated numerical experiments implementing full-scale modelling of the evolution process. Naturally, different initial states give rise to different paths of evolution, and the main problem is to discover the path consistent with the Earth's evolution. Examination of the entire evolutionary tree (rather, forest) of possible variants is capable of discouraging computermen. We could overcome this fundamental difficulty with the help of a 2-D mantle model specially developed for this approach and described in [Lobkovsky and Kotelkin, 2004]. Precisely the fast 2-D modelling, rather than prestigious but slow 3-D modelling, gives one a chance to choose the most realistic variant of the Earth's evolution from multiply calculated patterns of evolution developing from various initial states.
Fortunately, even test calculations revealed unstable equilibrium-state initial conditions leading to bursts of convection activity consistent with benchmark events of the Earth's history. The initial state was then updated using energy estimates obtained for the planetary accretion [Safronov, 1969; Vityazev, 1990]. Although these estimates are numerically somewhat different, they point to a precisely unstable hot post-accretionary state of the Earth's mantle.
A comprehensive series of experiments was conducted in order to enhance the activity bursts and improve the agreement between their duration and data of historical geology [Khain, 2001] by varying constitutive parameters of the model. As a result, a narrow range of values of the constitutive parameters was found in which well-pronounced peaks of geodynamic activity are observed; moreover, time moments of these peaks coincided remarkably well with formation datings of supercontinents [Lobkovsky and Kotelkin, 2004]. The smallness of the range of constitutive parameters within which the activity peaks are observed raises some doubts concerning the reality of this virtual variant, but these doubts are removed by the fact that the inferred optimal dimensionless values of the constitutive parameters are attained with real (dimensional) experimental data for the Earth's mantle.
Visualization and examination of detailed temporal behavior of thermochemical structures corresponding to the activity peaks have led to the discovery of mantle overturns [Lobkovsky and Kotelkin, 2004]. It was found out that simultaneous bursts of thermal and chemical components of the process enhance each other and lead to a resonance growth of single-stage circulation in the entire mantle, resulting in an immense exchange of material between the upper and lower mantle. Such crustal growth episodes, that occurred during the evolution of the Earth have been reliably fixed by geochemists from data on Nd-Sr isotopic compositions, trace elements and noble gas budgets, and Th/U ratio [Stein and Hoffmann, 1994].
It is clear that mantle overturns discovered with the help of 2-D modelling are spatial structures and their authentic configuration can be determined solely in terms of the 3-D modelling approach. A pertinent 3-D algorithm has been developed, adjusted, and tested. This paper presents the first results of 3-D modelling of thermochemical evolution from an unstable hot initial state of a spherical mantle layer.
Mantle material is regarded as an inertialess viscous fluid whose density inhomogeneities are described in the Boussinesq approximation,
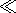 r0,
dr = dr th + dr ch + dr ph
r0,
dr = dr th + dr ch + dr ph representing the sum of thermal, chemical and phase variations.
The material model consists of the incompressibility condition and equations of motion and heat and mass transfer; in the Boussinesq approximation, this model is described by the following equations in dimensionless variables:
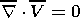 |
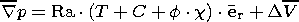 |
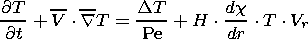 |
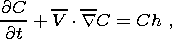 |
where the sought-for functions V, p, T and C are velocity, dynamic pressure, temperature and concentration, respectively; Ra and Pe are the Rayleigh and Peclet numbers; and the parameters f and H and the Heaviside function c(r - r ph) characterize the density jump, the thermal effect and the position of a phase transition. The source term Ch accounting for the generation of heavy and light fractions is specified below at the finite difference stage of the model realization.
A change in the position of the phase transition surface taken into account in
the equation of motion is controlled by
p-T conditions, from which the
argument of the Heaviside function
r ph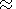 r0
ph - G
r0
ph - G (T ph - T0 ph) is found in the hydrostatic
approximation. However, assuming that the displacement
r ph - r0 ph and the tilt
G of the phase boundary are small, they are neglected
in the calculation of phase
heat generation in the heat conduction equation (this means that the phase
boundary is fixed and spherical and the normal velocity coincides with the
radial component
V r).
(T ph - T0 ph) is found in the hydrostatic
approximation. However, assuming that the displacement
r ph - r0 ph and the tilt
G of the phase boundary are small, they are neglected
in the calculation of phase
heat generation in the heat conduction equation (this means that the phase
boundary is fixed and spherical and the normal velocity coincides with the
radial component
V r).
Boundary conditions are formulated in the traditional form:
where t is the tangential stress.
Initial distributions of temperature and concentration should also be specified in order to examine evolution of the mantle layer. An averaged initial temperature was set in the form
 (r
- 1)].
(r
- 1)]. With A = 16, this formula yields a temperature distribution close to the estimate obtained in [Vityazev, 1990].
The numerical realization of the project included a finite difference
approximation of differential equations of the model on a uniform mesh in
Cartesian coordinates. The spherical layer was enclosed in a cube divided into
225
 225
225
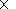 225 cells in the calculations described below.
An approximation of the
second order in spatial variables was used and the equations of heat and mass
transfer were integrated over time with second-order accuracy as well. The
boundary conditions were satisfied with first-order accuracy.
225 cells in the calculations described below.
An approximation of the
second order in spatial variables was used and the equations of heat and mass
transfer were integrated over time with second-order accuracy as well. The
boundary conditions were satisfied with first-order accuracy.
The force and the heat generation associated with the phase transition were converted to the unperturbed position of the phase boundary r0 ph = 7/8 and were approximated by one mesh layer (the jump dc/dr was spread over the mesh spacing).
Generation of the heavy and light material was modelled by analyzing, at each time iteration, the situation at mesh nodes located at a certain depth. In solving the problem of light fraction generation, the temperature at mantle nodes adjacent to the core is analyzed and, if the current temperature exceeds the melting point T melt, the value C light is ascribed the concentration at this node. As regards the generation of eclogite at mantle nodes located at the eclogitization depth (80-100 km), the radial velocity of material is analyzed and, if the material sinks, the C ecl is ascribed to its concentration. This modelling variant is justified in the case of the Earth because kinetics is a faster process compared to the slow stage of reactant supply limiting physicochemical transformations. At all other mesh nodes, the concentration is determined by the mass transfer equation with a vanishing source term Ch.
Small initial disturbances bringing the mantle out of the unstable equilibrium state were modelled by a random distribution of mantle density perturbations. No eclogites are present at the initial time moment. The initial distributions of temperature and concentration are shown in the first video frame.
Results presented in our work were obtained with the following values of parameters:
According to the similarity criteria
these values correspond to the following characteristic values of physical quantities:
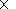 106 m, k
= 10-6 m2 s-1,
106 m, k
= 10-6 m2 s-1,
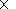 10-5 (o)-1,
cp = 1.25
10-5 (o)-1,
cp = 1.25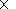 103
J (kg
103
J (kg o)-1,
o)-1,
 1022
kg (m
1022
kg (m s)-1, g
= -4.4 MPa (o)-1.
s)-1, g
= -4.4 MPa (o)-1.

|
| Figure 1 |
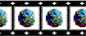
|
| Animation 1 |
As seen from Animation 1, the geodynamic process starting from an unstable initial state attains a nearly cubic pattern of whole-mantle convection with vigorous hot plumes rising from interiors of the planet toward the surface and with eight heavy avalanches penetrating the mantle at triple junctions of convective cells: this is the first overturn in the Earth's history. At this stage, the velocity reaches its maximum value (40 cm yr-1 ) and the layer rapidly assumes a stable state. This stage is followed by an epoch of slow small-scale Archean evolution that is diagnosed well by a quasi-homogeneous network of collisional boundaries (colored blue) on the outer surfaces of the layer. The annular cross section and the inner hemisphere projections show a gradual cooling of the upper mantle and heating of the lower mantle. At a time moment when critical thermochemical partitioning between the upper and lower mantle is attained, the motion is dramatically reorganized, giving rise to a well-pronounced post-Archean mantle overturn that involves one descending flow in the region of the equatorial plane two ascending superplumes at the poles. A system of plumes in the upper mantle is observed in the equatorial cross section in the part of the layer opposite to the sink. As is evident from the outer projections, the post-Archean overturn (the second in the history of the Earth) forms a qualitatively different, global system of rare collisional belts; i.e. large lithospheric plates form on the planet.
A new mantle overturn develops 700 Myr later; this time, a funnel-shaped sink of heavy upper mantle material forms in another place of the equator and a powerful superplume (along with the polar superplumes) is observed in contrast to a few isolated plumes in the part of the layer opposite to the sink. Thus, this overturn leads to the opening of three oceans and a reorganization of the system of outer collisional belts.
The formation and the whole subsequent evolution of equatorial sinks can be clearly traced in the annular cross section of the mantle layer, and the overturn-related spreading of heavy material over the Earth's core is well observable in the projection of the inner radial cross section of the layer. In particular, the initially symmetric front of spreading heavy material (colored blue) is seen to lose stability and assume a broken shape, and well-observed chaotically branching structures (inner collisional boundaries colored red) mark the motion of light material driven from the core surface.
The fourth and fifth overturns display qualitatively similar evolutionary patterns, but the amplitudes and lifetimes of event vary, and the activity peaks seen in Figure 1 become shorter and smoother, whereas each new overturn shortens periods of low geodynamic activity separating these peaks. Note that during the fifth overturn, when a concentrated funnel-shaped sink is displaced from the equatorial plane, the outer projection displays more adequately vast horizontal movements of material and the reorganization of the plate system in the lithospheric shell of the planet.
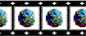
|
| Animation 2 |
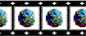
|
| Animation 3 |
Before analyzing our numerical results, we remind the reader the idealized stationary conditions under which these results were obtained: the Earth's core does not cool, chemical resources of eclogitization and differentiation of the mantle are inexhaustible, and the thicknesses of the mantle and its upper and lower parts are invariable. Even under these fixed conditions, the hot initial state defined with terrestrial values of constitutive parameters is sufficient to yield the remarkable phenomenon of a resonant evolutionary process.
Long epochs of gradual evolution are interrupted by mantle overturns radically changing the state of the mantle. The mantle overturns, changing the face of the planet, are combinations of a superavalanche and superplumes that occur simultaneously and increase material velocities by many times. Elucidation of the origin of the observed events is a problem of basic significance. Within the framework of purely thermal convection, such an origin is the barrier role of the endothermic phase transition separating the upper and lower mantle.
Our model opens new possibilities for activation of the geodynamic process. Cooling of the mantle enhances the role of density inhomogeneities of chemical origin whose values remain constant in the model studied. First, chemical processes enhance the nonlinear character of motions, now accelerating thermal convection, now decelerating it; second, they have a significant effect on the intermittent behavior of mantle convection, facilitating the overcoming of the 670-km phase barrier; and third, they produce their own recurrent local-scale activity bursts in both upper and lower mantle. These properties of the chemical component in our model (weakly expressed in the experiment illustrated in Figure 1) can be clearly observed if extreme values are artificially ascribed to the chemical heterogeneity amplitudes C ecl and C light.
In light of the above considerations, an abrupt increase in geodynamic activity during a mantle overturn can be accounted for by a nonlinear interaction (in particular, via the hydrodynamic stress field) of concurrent thermal and chemical components of the convective process. A wide spectrum of transformations induced by developed convection in liquid media is capable of producing, for a time, a unified global (whole-mantle in every sense) convective configuration. In practice, an important factor prerequisite for this phenomenon to occur is a concentrated primary impetus that can ensure an unstable post-accretionary state of the planet.
It is clear that the energy of such powerful global phenomena as overturns is sufficient for assembling supercontinents and opening oceans, making the appearance of the planet asymmetric; and contrariwise, it is difficult to find other mechanisms of such transformations. Thus, the numerical experiment presented in this paper provides the best explanation of the Wilson cycles. Our model results were brought into agreement with the duration of Wilson cycles (700-900 Myr) by fitting model values of the Rayleigh number (due to uncertainties in the effective viscosity coefficient). Therefore, we do not pretend to have obtained Wilson cycles but associate with them the inferred virtual cycles. It is remarkable, however, that convective velocity scales, also controlled by the Rayleigh number, assume real values (1-12 cm yr -1 ).
The amplitude of overturns and the time interval between them decrease with each next global cycle. Cooling of the mantle leads to disintegration of global overturns into smaller (continental-scale) breaks of the phase barrier [Lobkovsky and Kotelkin, 2004] that can be conveniently referred to as avalanches. We associate such regional-scale breaks with the Bertrand geologic cycles (170 Myr long). Within the framework of our model, it is also natural to assume that the Bertrand cycles are controlled by the differentiation of mantle material at the boundary of the iron core, and the Stille cycles (35 Myr) are controlled by the chemical partitioning of the mantle at its boundary with the crust and the subsequent eclogitization of mantle material.
Fukao Y., S. Maruyama, M. Obayashi, and H. Inoue (1994), Geologic implication of the whole mantle P -wave tomography, J. Geol. Soc. Japan, 100(1), 4-23.
Keondzhyan, V. P., and A. S. Monin (1980), On the concentration convection in the Earth's mantle, Doklady AN SSSR (in Russian), 253(1), 78-81.
Khain, V. E. (2001), Large-scale cyclicity, its possible origins, and a general trend of the Earth's tectonic history, in Fundamental Problems of General Tectonics (in Russian), pp. 403-424, Nauchnyi Mir, Moscow.
Kobozev, A. V., and V. P. Myasnikov (1987), A three-dimensional evolutionary model of the inner structure of planets, Doklady AN SSSR (in Russian), 296(3), 561-565.
Lobkovsky, L. I., and V. D. Kotelkin (2004), Numerical analysis of geodynamic evolution of the Earth based on a thermochemical model of the mantle convection, Russian J. Earth Sci., 6(1), 1-10.
Machetel, F., and P. Weber (1991), Intermittent layered convection in a model mantle with an endothermic phase change at 670 km, Nature, 350, 55-57.
Maruyama, S. (1994), Plume tectonics, J. Geol. Soc. Japan, 100(1), 24-49.
Monin, A. S., D. G. Seidov, O. G. Sorokhtin, and Yu. O. Sorokhtin (1987a), Numerical simulation of mantle convection, Doklady AN SSSR (in Russian), 294(1), 58-63.
Monin, A. S., D. G. Seidov, O. G. Sorokhtin, and Yu. O. Sorokhtin (1987b), Numerical experiments on mantle convection patterns, Doklady AN SSSR (in Russian), 295(5), 1080-1083.
Myasnikov, V. P., and E. G. Markaryan (1977), A hydrodynamic model of the Earth's evolution, Doklady AN SSSR (in Russian), 237(5), 1055-1058.
Myasnikov, V. P., and V. D. Savushkin (1978), Application of the perturbation method to hydrodynamic modeling of the Earth's evolution, Doklady AN SSSR (in Russian), 238(5), 1083-1086.
Safronov, V. S. (1969), Evolution of the Protoplanetary Cloud and Formation of the Earth and Planets (in Russian), 244 p., Nauka, Moscow.
Solheim, L., and W. Peltier (1994), Avalanche effects in phase transition modulated thermal convection: A model of Earth's mantle, J. Geophys. Res., 99(B4), 6997-7018.
Stein, M., and A. W. Hofmann (1994), Mantle plumes and episodic crustal growth, Nature, 372, 63-68.
Tackley, P., D. Stevenson, G. Glatzmaier, and G. Schubert (1993), Effects of an endothermic phase transition at 670 km depth in a spherical model of convection in the Earth's mantle, Nature, 361, 699-704.
Vityazev, A. V. (1990), Early evolution of the Earth, Zemlya i Vselennaya (in Russian), (2), 18-24.