E. L. Afraimovich1, E. I. Astafieva1, M. B. Gokhberg2, V. M. Lapshin2, V. E. Permyakova2, G. M. Steblov2, and S. L. Shalimov2
1 Institute of Solar and Terrestrial Physics (ISTP), Irkutsk, Russia
2 Institute of Physics of the Earth, Russian Academy of Sciences,
Moscow
The ionospheric effects produced by seismic activity attracted geophysicists since a few dozens of years ago [Buchachenko et al., 1996; Gokhberg et al., 1990; Ondoh, 1999; Pertsev and Shalimov, 1996]. This was caused by the acute need of the timely prediction of large earthquakes that cause numerous destructions and many hundreds of human deaths for a year. In this respect the study of the ionosphere state before large earthquakes is one of the most important tasks of modern geophysics and radiophysics.
At the present time many experimental facts prove the existence of electromagnetic and plasma anomalies, such as the disturbed parameters of various fields and plasma, generated in the atmosphere and ionosphere hours, days, or weeks before the time of an earthquake. Convincing data are available for quasisteady electric fields in the earth and ionospheric plasma, for the disturbances of the basic parameters of the E - and F -regions in ionospheric plasma [Alimov et al., 1989; Liperovskii et al., 1990; Ondoh, 1999], omit changes in the plasma ion composition and temperature and for variations of high-energy particle fluxes in the upper ionosphere [Parrot, 1994].
During the last decade several satellite experiments discovered new phenomena in the ionosphere and magnetosphere, that had preceded the earthquakes. In particular, these are the anomalous increase of electromagnetic radiation in the ranges of ultralow, extremely low, and very low frequencies, recorded during the space missions of the "Interkosmos-18 and -19'', "Oreol-3'', "Kosmos-1809'', "Interkosmos-24'', and some other spacecrafts [Buchachenko et al., 1996]. The existence of extremely low-frequency radiation of seismic origin in the ionosphere was proved by the results of the statistical analyses of satellite data recorded for hundreds of earthquakes [Parrot, 1994]. The experience of predicting Kamchatka earthquakes based on the measurements of very low-frequency electromagnetic radiation has been reported by Druzhin [[2002].
However, in spite of the numerous observations, there is still no generally accepted view that would allow one to interpret the observations of the ionosphere in seismically active regions, in spite of the fact that there are plenty of hypotheses. It should be noted that ionospheric heterogeneities and effects that are associated with them also remain after earthquakes; heterogeneities are recorded both in the neutral and also in the ionized components of the ionosphere, the spacial sizes of the disturbances being significant.
There are still no reliable technologies for predicting earthquakes by using the radiophysical monitoring of ionospheric processes. The insufficient sensitivity, low space and time resolution, the small number of respective radio-wave propagation paths, used to monitor radio-signal parameters, and the lack of global continuous measurements, characteristic of conventional means for radio sounding, preclude the solution of this problem.
New hopes in the study of the seismic and ionospheric interaction have been associated recently with the development of a global positioning system (GPS) and with the creation on this basis of widely branching permanently operating global and regional networks of GPS stations, including at least 1000 sites by the beginning of 2002, the data of which are delivered to the Internet system [Davies and Hartmann, 1997; Klobuchar, 1997]. At the present time the potential of this network is growing substantially at the expense of using compatible, multichannel, two-frequency receivers capable of receiving signals from the similar Russian GLONASS navigation system [Klobuchar, 1997]. Moreover, investigators can also use the conventional software which allows one to unify the primary processing of the GPS-GLONASS data.
One of the most important constituents of the global GPS network is the International GPS Service (IGS) which is widely used to monitor geodynamic processes with previously unprecedented accuracy of crustal deformation displacements. Simultaneously many efforts are given to develop methods for the diagnostics and monitoring of ionospheric processes, including those caused by seismic and ionospheric relationship.
It is obvious that the reliability of determining the basic characteristics of the seismic and ionospheric interaction calls for a large number of GPS stations, which is especially important for seismically active regions.
The dense network of the GPS sites, the data of which are available in the Internet has been developed in the seismically active zone of California, USA. The operation of more than 300 GPS sites, recording up to 5-8 IGS GPS signals provides the unprecedental space resolution (up to 2000 IGS rays-GPS receiver, line-of-site, LOS). This allows the development of a system for the continuous monitoring of seismic and ionospheric effects in this region. This network is already intensively used to investigate ionospheric disturbances of various types [Afraimovich et al., 2003, 2004b; Calais et al., 2003].
Another more powerful network, known as GEONET which includes 1000 GPS detectors, is used in Japan [Saito et al., 2001; Tsugawa et al., 2003]. However, until the present time the data of this network are not available for free use in the Internet network.
The Kamchatka regional network of stationary sites recording GPS signals (KAMNET) has been operating continuously since 1996 in the seismically active zone in the Kamchatka Peninsula. It had been designed for geodynamic investigations [Levin et al., 2002]. This network covered a "white spot'' in the global GPS network. The data of this network can be used to study seismo-ionospheric effects.
Hence, the experimental basis of GPS monitoring in the main seismically active regions has been created. Many papers were published for detecting acoustic shock waves generated during earthquakes using GPS data [Afraimovich et al., 2001b, 2001c, 2001d; Calais and Minster, 1995; Calais et al., 1998b], and also generated by large industrial explosions [Calais et al., 1998a; Fitzgerald, 1997]. However, the results of these studies cannot be used directly for solving the problem at hand.
No answer has been yet found for the omit possibility of discovering earthquake precursors during the transionospheric sounding using GPS signals under the conditions of quiet and magnetically disturbed ionosphere. In general this concerns the entire complex of seismo-ionospheric relationship. The purposeful search for earthquake precursors using GPS data has just been initiated. There are still a few publications directly devoted to this problem [Astafieva et al., 2002].
The aim of this paper is to analyze the potential possibilities of GPS monitoring during the detection of potential earthquake precursors using the Hector Mine earthquake of October 16, 1999, in California as an example.
The choice of this event was based on the fact that during the time of this fairly large earthquake (M=7.1) a dense network of land-based GPS recording units was operating, which provided a fairly high spacial resolution.
Section 2 presents the general characteristics of the 16.10.1999 experiment. Sections 3 and 4 provide the detailed analysis of variations in the total energy content (TEC) during the sufficiently long period of time including the day of the earthquake (October 13 to 18, 1999) for two basic types of the known seismo-ionospheric effects:
(1) quasi-regular variations of the ionosphere parameters;
(2) generation of internal gravity waves (IGW).
The aim of Section 5 is to discuss the prospects of detecting small-scale ionospheric heterogeneities, supposedly arising during the period of earthquake preparation, using the results of the special measurements of the magnitude and phase scintillations of the GPS signals.
The reviews of literature available and the description of the methods used are given separately in each pertinent section of this paper. It should be noted that the physical mechanisms of the seismic and ionospheric effects concerned are not discussed in this paper.

|
| Figure 1 |
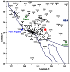
 3 km. The position of the epicenter is shown
in the
schematic map of the California region (Figure 1).
3 km. The position of the epicenter is shown
in the
schematic map of the California region (Figure 1).
We analyzed the seismic, geomagnetic, and ionospheric data available for this region for period of October, 13-18, 1999 (286th to 291st days) four days before and two days after the earthquake.

|
| Figure 2 |
The data for the Dst and Kp geomagnetic indexes for October 13-18, 1999, were obtained at the WDC Site. The value of the Kp index varied form 2 to 4 and was 5 in October 15, 1999. The Dst index varied from 20 to 60 nT with the maximum deviation of up to 70 nT a day before the earthquake (Figure 2a). This allows one to rank this time interval as a period of moderate magnetic activity.
To analyze the local geomagnetic situation in California we also used the data of the nearest magnetic variation measurement sites: FRN (37.08o N, 240.28o E) and TUC (32.17o N; 249.27o E). The locations of these sites are shown by crosses in Figure 1; the analysis of these data is given in Section 4.2.
The state of the ionosphere in the epicenter region was estimated using the data recorded by the GPS and the nearest Point Arguello ionospheric measurement station (32.17o N; 249.27o E), the data of which are provided at the [SPIDR] Site; the position of this station is shown by a rhomb in Figure 1.
The positions of the GPS stations are shown by bold-type dots in Figure 1. Due to space limit only the names of some sites are given. For the same reason the coordinates of the sites are not given; their exact parameters can be found in the [SOPAC] Site. We processed the data from about 125 sites.
In this paper we used the primary data of the global GPS network in the RINEX format (Site [SOPAC]), and also the secondary data for the absolute values of the vertical total electron content (TEC), I0, in the IONEX format, plotted using the GIM technology at the EMRG Laboratory ([IONEX] Site).
In addition, an attempt was made to discover, using the GPS data, the potential variations of the daily TEC data and variations in the TEC data caused by the propagation of Internal Gravity Waves (IGW) which can be generated in the earthquake preparation region, as follows from the hypothesis discussed here in Section 4.
Some authors (e.g., [Alimov et al., 1989; Liperovskii et al., 1990; Ondoh, 1999]) reported the quasiregular disturbances of the ionospheric E - and F -regions parameters in active seismic regions, including changes in the ion composition, plasma temperature, and the fluxes of high-energy particles in the upper ionosphere [Parrot, 1994], which preceded the earthquakes.
For instance,
Ondoh [1999]
reported a disturbance in the diurnal variation of the critical
f0F2 frequency
and in the height
h F variations before
the earthquake of magnitude 7.8 that occurred near
Hokkaido on July 12, 1993, 3 nights before and 3 nights after the
earthquake. The
f0F2 values decrease
below the average monthly median for this period of time, whereas the height
h
F variations before
the earthquake of magnitude 7.8 that occurred near
Hokkaido on July 12, 1993, 3 nights before and 3 nights after the
earthquake. The
f0F2 values decrease
below the average monthly median for this period of time, whereas the height
h F increased three
nights
before and decreased three nights after the earthquake. This period was devoid of
any solar flares or
geomagnetic disturbances and the local geomagnetic conditions were quiet. Therefore,
these variations can
be classified as seismoionospheric manifestations. However, the relative deviations
of these values from the
median ones were not higher than 20%, this making us not quite sure in this conclusion.
F increased three
nights
before and decreased three nights after the earthquake. This period was devoid of
any solar flares or
geomagnetic disturbances and the local geomagnetic conditions were quiet. Therefore,
these variations can
be classified as seismoionospheric manifestations. However, the relative deviations
of these values from the
median ones were not higher than 20%, this making us not quite sure in this conclusion.
We analyzed the data recorded by the Point Arguello ionosphere measurement station (32.17o N; 249.27o E) located in California. Figure 2b presents variations in the critical frequency of the f0F2 layer (unfortunately, there are no data for the day preceding the Hector Mine earthquake). Our analysis of the f0F2 variations did not reveal any notable variations in the daily f0F2 behavior similar to those reported by Ondoh [1999]. The daily f0F2 variation agrees well with the normal trend with a maximum in the vicinity of 14 LT (the local time scale for the 240o E longitude is given at the bottom of Figure 2). Neither did we find any specific behavior of the critical frequency variations recorded for the Es sporadic layer using the data of the Point Arguello ionospheric measurement omit, which might have been expected before the earthquake (as reported, for example, by Kolokolov et al., 1992).
To study quasiregular variations in the ionosphere using GPS data we used a new technology for plotting the global maps of the absolute "vertical'' TEC I0 value using the data of the International IGS-GPS network (Global Ionospheric Maps (GIM) technology). These map with a two-hour resolution can be found at the IONEX Site.
Note, that one of the problems arising when Global Ionospheric Maps are used to study TEC variations is 3-D interpolation used to make these maps. The random distribution of GPS receivers over the globe and a need for getting TEC data distributed over a uniform network in order to plot global maps results in the different quality of data in various regions. Another problem is associated with the fact that the TEC maps provided in the Internet have a two-hour resolution, which precludes the quantitative analysis of the TEC dynamics.
Figure 2d shows variations of the absolute vertical TEC I0(t) values obtained from the IONEX data of the EMRG Laboratory for the coordinates of 35o N and 245o E; the average I0(t) values correspond to the position of the column centers, and the RMS value, to their vertical size. In our study we used the TEC unit equal to 1016 m-2 which is commonly used in the literature.
One can see that the diurnal variation of I0(t) agrees with the normal one and correlates well with the diurnal variation of the f0F2 critical frequency (see Figures 2b and 2d). It should be noted that even if there were any disturbances in the TEC diurnal variation before the earthquake, they would have hardly been recorded because of the low potential and real accuracy of reconstructing I0(t) in terms of the GIM technology, represented by RMS error series in Figure 2d.
Thus it can be concluded that the quasiregular variations of the ionosphere parameters are controlled in this case by the local time and geomagnetic situation.
Some authors [Gokhberg and Shalimov, 2000; Gokhberg et al., 1996; Pertsev and Shalimov, 1996; Pilipenko et al., 2001; Shalimov, 1992] discussed models for omit internal gravity wave (IGW) generation in the region of a future earthquake omit as a consequence of the activization of lithosphere-ionosphere interaction. These atmospheric waves produce, as they propagate to the ionosphere, plasma disturbances sufficient to cause plasma instability which results in the origin of ionospheric heterogeneities of different scales. It has been proved theoretically and experimentally that long-period internal gravity waves can initiate the development of plasma bubbles or regions of low-density plasma (because of Reileigh-Taylor instability in the equatorial ionosphere and Perkins instability in the middle-latitude ionosphere) [Kelley, 1989]. At the same time distinct plasma heterogeneities, such as, the boundaries of the bubbles, can act as sources producing extremely low- and very low-frequency waves which are recorded by the spacecrafts [Larkina et al., 1983]. Later, the neutral component begins to move upward as a result of the development of Reileigh-Taylor and Perkins instabilities, the formation of plasma depleted regions, and the subsequent heating of the neutrals. This upward movement of the neutral component results in the growth of the plasma density above the F layer maximum, because it would prevent the plasma to "flow'' into the region of high recombination [Ivanov-Kholodnyi and Mikhailov, 1980].
To conclude, internal gravity waves can be taken as the main attributes of the lithosphere-ionosphere relations in seismically active regions. This seems to be even more natural taking into account the fact that the stratification of the atmosphere promotes the intensification of the neutral component disturbances arising in the vicinity of the Earth surface. The presence of acoustic (infrasound) disturbances has not been proved by direct observations in earthquake-prone regions. At the same time, it is in these regions that favorable conditions exist for the predominant generation of internal gravity waves (IGW).
Internal gravity waves (IGW) manifest themselves in the ionosphere as travelling ionospheric disturbances (TID) which are usually detected by various radiophysical tools. TIDs are usually classified as large- and medium-size disturbances, differing in their horizontal phase velocity which is higher or lower than the sound velocity in the lower thermosphere (roughly 300 m s -1 ) and in their periods of 0.5-3.0 hours and 15-60 minutes, respectively [Hines, 1960; Hocke et al., 1996; Oliver et al., 1997].
Medium-scale TIDs are recorded primarily in the day time and are usually associated with internal gravity waves (IGW) which are generated in the lower atmosphere. Large-scale TIDs predominate during the night hours and are closely associated with geomagnetic and aurora activities [Hunsucker, 1982]. It is known that internal gravity waves of natural origin can be produced not only by earthquakes but also by other natural phenomena, such as, magnetic storms, aurora-related phenomena, weather fronts, tropospheric turbulence, jet flows, solar terminator, and volcanic eruptions [Hocke et al., 1996; Oliver et al., 1997; Somsikov, 1995]. Internal gravity waves (IGW) can be generated also by artificial effects, such as, man-made explosions, heating by high radio radiation, launching of heavy rockets, and chemical discharges from space vehicles.
As a consequence, the observed pattern of an electron concentration disturbance is essentially the total interference wave field of internal gravity waves of different origins. For this reason, the discovery of internal gravity waves, potentially generated in the epicenter at the stage of earthquake preparation, is a fairly hard task.
Its solution requires the use of the maximum complete set of indications distinguishing between the background internal gravity waves (IGW) and the gravity waves generated in the epicenter region. These indications may include the geometry of the source (this source being almost a point source compared with the aurora IGW source or with the terminator), the characteristics of the IGW vector, IGW spectral and dispersion characteristics (variation of the velocity and direction of propagation vs. period), to name but a few.
The identification of the internal gravity waves of seismic origin during the detection of a respective moving ionospheric disturbance (TID) is a difficult task, the versions of its solution depending on weather the respective TID was located in the near or far zone of the source. The relationship between the far zone radius R0 of the IGW source and the linear size L of the region where the ionospheric IGW response of internal gravity waves (IGW) are distributed with the synphase interval Dj=p/4 has the form
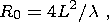 | (1) |
where l is the IGW length.
The Dj=p/4 phase shift of the signals recorded in different subionosphere sites, where these signals will be taken to be in equiphase condition, and the wave front to be flat, corresponds to the time interval of T /8. For the average TID value T = 2000 s [Hocke et al., 1996; Oliver et al., 1997] this interval is 250 s, the value exceeding the error of this method, controlled by the 30-second GPS measurements.
In the case of the Hector Mine earthquake, using the average values L = 500 km and l = 400 km (with the IGW velocity of about 200 m s-1 ), the boundary of the far zone of the TID source is controlled by the radius R0 = 2500 km, that is, far beyond the dense GPS network in California. The horizontal distances of the recording sites from the earthquake epicenter are less than R0, the epicenter itself being located inside the region of the GPS sites distribution (see Figure 1). Consequently, the IGW ionospheric responses can be recorded in the near zone of the earthquake epicenter, which calls for the use of a spherical wave model. Where the analysis of the experimental data is able to locate the source of spherical waves and to determine its coordinates, we can discriminate between the IGW from this source and the waves associated with aurora activity.
The getting of this information was facilitated by the availability of the dense networks of GPS receiving sites. This called for the use of the modern methods of space-time data processing based on the concept of phase-locked antenna grids [Afraimovich, 2000; Afraimovich et al., 2002a].
As a first step, we will limit ourselves to the analysis of merely the spectral characteristics of TEC disturbances, average for the California network of GPS sites (see Section 4.4).
The main volume of information about the structure and dynamics of ionospheric disturbances during the transionospheric sounding by GPS signals is contained in the variations of the "oblique'' total electron content Is(t), found from the results of measuring the phase delay of GPS signals using two working frequencies: f1 =1575.42 MHz and f2 = 1227.60 MHz [Hofmann-Wellenhof et al., 1992]:
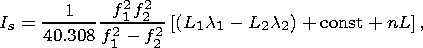 | (2) |
where L1l1 and L2l2 are the increments of the radio signal phase path, caused by the delay of the phase in the ionosphere (m); L1 and L2 are the numbers of the full phase rotations; l1 and l2 are the wavelengths (m) for frequencies f1 and f2; const is some unknown initial phase route (m); nL is the error of phase route determination (m).
The phase is measured in the GPS system with a high accuracy for which the error in determining TEC with 30-second averaging intervals is not higher than 1014 m-2, even though the initial TEC value remains unknown [Hofmann-Wellenhof et al., 1992]. This allows one to detect ionization heterogeneities and wave processes in the ionosphere in a wide range of the values of amplitudes (up to 10-4 of the daily TEC variation) and periods (from days to 5 min). Where a group delay is measured, one can estimate the absolute TEC value although with a much lower accuracy.
In order to eliminate uncertainties in localizing the IGW ionospheric response caused by the integral character of the TEC value, we can assume that the TEC value is formed at the point where the ray of vision onto IGS intersects with the IGS plane at the height hd of the maximum ionization region F of the ionosphere, which has the major contribution to the TEC formation.
When choosing the hd value one should take into the consideration the fact that the decline of the electron concentration with the height above the peak of the F2 layer proceeds significantly more slowly than below the maximum. Since the variation of the concentrations with the height is actually a "weight function'' of the TEC response to a wave disturbance [Afraimovich et al., 1992], it is reasonable to replace hd by a value that exceeds the true height of the layer, h max, by a value of about 100 km (the h max value itself varying over the range of 250-350 km depending on the time of the day and on some geophysical factors which can be accounted for if necessary). As the first approximation, we can assume that it is at this altitude that the ionospheric response of IGW is recorded in the TEC variations.
The magnitude dI of the TEC disturbance, caused by the IGW propagation, experiences a high aspect-angle variation because of the integral character of trans-ionospheric sounding. The maximum dI amplitude corresponds to wave disturbances, the K vector of which is perpendicular to the direction of r to IGS [Afraimovich et al., 1992; Mercier, 1996]. In order to reconstruct the maximum dI amplitude, one has to use information available for the angles of the IGS arrival and for the TID wave vector [Afraimovich et al., 1998]. The relative magnitude of this dI/I response is controlled by the I background value for which one can use the absolute "vertical'' TEC value, I0; this information can be obtained from IONEX, namely from TEC maps in the Internet [Mannucci et al., 1998].
The most reliable results of estimating TID parameters can be obtained for the high angles of the ray site qs(t) in IGS, because the sphericity effects in this case become sufficiently small. In our study all results were obtained for the angles larger than 30o. In this case, however, the range of IGW periods, detected from the GPS data, is limited from above by the value of 60-90 min, because the critical duration of the continuous phase measurements of the chosen IGS signals does not exceed 3-4 hours for the local angles larger than 30o.
It is practically impossible to use the absolute vertical I0 value in the IONEX format to monitor TID data because of the low accuracy of the I0 reconstruction and the low resolution in time (see Section 3).
The primary data in this study were the series of the "oblique'' TEC Is(t) values, and also the series of the azimuth as(t) values and the angle of the site of the qs(t) ray in the IGS, calculated using the CONVTEC Program developed at the Institute of Physics of the Earth, which transforms the standard GPS RINEX files standard for the GPS RINEX System. Continuous Is(t) measurement series with lengths of not less than 2.3 hours were chosen to determine the TID characteristics.
The TEC disturbance magnitudes were normalized using the transformation of the "inclined'' TEC into its equivalent vertical value [Klobuchar, 1986]
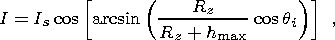 | (3) |
where Rz is the radius of the Earth; h max is the height of the maximum of ionospheric layer F2. The variations of the regular ionosphere, as well as the trends introduced by the satellite movement, are removed using a procedure for removing a trend with a time window suitable for a particular experiment
|
| Figure 3 |

|
| Figure 4 |
RMS error of the TEC variations was calculated for each dI(t) series, as long as 2-3 hours, filtered over the above-mentioned period ranges. These values were then averaged over all of the data series obtained for each site of the California network and for each IGS time interval (about 800 series for a given hour interval). 132 time intervals were processed for the six days with a time shift of 1 hour (22 intervals per day).
Figure 4c, shows the columns of the RMS A(t) variations of the total electron content dI(t) in the period range of 32-128 minutes. Indicated in the figure are the A and B time intervals for which TEC variations, measured at Site AZU1, are presented in Figure 3. Similar relationships are presented in Figures 3d and e, for the periods of 10-25 minutes B(t) and 2-10 minutes C(t), respectively. The local time scale is given below for the 240o E longitude. The vertical line marks the time of the main shock.
It should be noted that the A(t) and B(t) diurnal variations are identical. Figure 3 shows that the magnitude of the TEC variations in the day time (A interval) is considerably larger than in the night time (B interval). The C(t) relationships, responsible for smaller heterogeneities (Figure 4e), differ markedly from the variations typical of the medium-size heterogeneities. The highest RMS values of the C(t) variations were observed in the early morning rather than in the local mid-day time.
The averaging over the whole site network and IGS sites confirms this regular relationship. This is associated mainly with the normal daily TID intensity variations in the poorly disturbed ionosphere, when maximum TEC variations are observed during the local midday TEC variations [Afraimovich et al., 1999; Davies, 1980].
However, it is well known that the TEC variation magnitude is controlled not only by the local time, but also by changes in the magnetic field intensity. This is illustrated in Figure 4a, which shows the H(t) variation of the horizontal component of the geomagnetic field for the FRN magnetic variation site (37.08oN; 240.28oE). The H(t) variations for the nearest site of the INTERMAGNET TUC net (32.17o N; 249.27o E) are fairly similar to the data of the FRN site. For this reason they are not presented graphically here.
The comparison of the dH(t) variations, filtered from the H(t) data series in the period range of 32-128 minutes (Figure 4b), with a relationship for TEC variations over a period range of 32-128 minutes, average for the Californian network of GPS RMS A(t) TEC variations in the range of 32-128 minutes, showed that there was no correlation between these relationships.
However, there is good correlation between the inverted - H(t) relationship, smoothed using a three-hour window (plotted in Figure 4c, as a thick line), and RMS A(t) variations of TEC dI(t) in the period range of 32-128 minutes. This specific feature could be explained by the fact that the clearly expressed daily relationship is characteristic not only of the TEC variation magnitude, but also of the strength of the quiet magnetic field of the Earth. However, the geomagnetic activity during the time period concerned was not quiet but moderate (see Section 2 and Figure 2).
Therefore the observed correlation seems to demonstrate a closer relationship between the magnetic field variation and the TEC variations of the IGW period range, compared to those proposed earlier.
The data reported by Afraimovich et al. [2001a, 2003] for the mid-latitude ionospheric response to geomagnetic disturbances suggest their decisive role in the formation of the TEC variation spectrum. These authors proved that the sudden onsets of magnetic storms had been accompanied by a negative TEC disturbance throughout the diurnal side lasting about 20 minutes, which lagged 3-10 minutes behind the sudden onset and moved from the day to the night side with a velocity of 10-20 km s -1 [Afraimovich et al., 2003].
The growth of the geomagnetic disturbance level was accompanied by the growth of the magnitude of the middle-latitude TEC variations in the IGW period range, this growth correlating with changes in the AE index variations (with the maximum correlation coefficient of 0.7) and in the Dst time derivative (with the correlation coefficient of - 0.9), and lags behind the maximum value of the Dst derivative and the AE index by about two hours. As the auroral oval widens as far as the middle latitudes, the region with the well developed middle-size TEC structure grows wider, too [Afraimovich et al., 2001a]. This agrees with the view that the periods of geomagnetic disturbance are dominated by TID disturbances which are generated in auroral regions and move toward the equator with a velocity of about 300-400 m s-1 [Hunsucker, 1982].
To conclude, the dominant geomagnetic control of the entire spectrum of ionospheric disturbances can serve as a serious obstacle in discovering potential seismo-ionospheric effects at the background of even moderate magnetic storms, if no specific means of recording ionospheric disturbances of seismic origin are found.
Our analysis has shown that the discovery of internal gravity waves (IGW), generated in the region of a future earthquake epicenter, using merely spectral characteristics (variations in the magnitudes of TEC variations in the IGW period range) seems to be hardly possible. Therefore the next step is to use the modern methods of the space-time processing of the data.
One of these methods is based on the concept of phased antenna grids [Afraimovich, 2000; Afraimovich et al., 2002a; Calais et al., 2003]. The second approach is to use the method of statistically optimal signal detection [Kushnir et al., 1990]. Finally, the third approach is to discover smaller-scale ionospheric heterogeneities produced by the IGW dissipation in the ionosphere [Kelley, 1989]. Below we will discuss the two latter potential techniques.
The specific problem of locating TEC variation anomalies is associated with the fact that the detected signal need be treated as the realization of a random process, the spectral density of which is unknown. At the same time the spectral density of random noise which masks the signal can be estimated preliminarily and, hence, can be treated as a known one. We detected anomalies using a statistically optimal wide-band detector after the periodic fluctuations were removed using the procedure of rejector filtering. A similar detector was described by Kushnir et al. [1990]. This detector is based on the Bayes optimum rule used to verify statistical hypotheses for the characteristics of a scalar z(t) data series observed in a sliding [z(t), z(t+T)] time window. The simple hypothesis H0 implies that the process observed in the [z(t), z(t+T)] window is a random process with a known spectral density, which is verified relative to a more complex alternative that the H1 values observed in the [z(t), z(t+T)] window include a random signal with unknown spectral density. The detection algorithm must include a procedure for estimating the spectral density of a scalar random process. The estimation is performed by way of deriving an autoregression (AR) model [Box and Jenkins, 1970].
The statistical detector filters the data using a recursive filter based on the previously estimated coefficients of the AR model. After this procedure the initial problem of signal detection reduces to the problem of detecting a random process segment with unknown spectral density against the background of white noise. The process of signal detection is based on the comparison of the likelihood ratio for the H0 and H1 hypotheses with a threshold value, the excess of which proves the existence of a signal. Since the signal detection is performed in a sliding window, the detector statistics is a time series, the length of which coincides with the length of the initial series diminished by a value equal to the T window length.

|
| Figure 5 |

|
| Figure 6 |
This time interval was chosen because, as mentioned above, the ionosphere was moderately disturbed. The periods of magnetic disturbances (associated with auroral electrojet intensification and with the heating of the neutral component of the ionosphere) usually lasted 30 minutes to 3 hours. The ionospheric disturbances in the range of 10 to 20 minutes might have been associated with the nonlinear processes of energy transfer from some disturbances of larger scale or with the inferred IGW effect from the seismic source.

|
| Figure 7 |
On the other hand, assuming that there is an IGW source in the range of 10-20 minutes from the epicenter of an impending earthquake, we can expect the arrival of a maximum signal caused by the arrival of internal gravity waves from the earthquake preparation zone at the bull and apex stations located at distances of 1.5o to 2o from the epicenter.
Note that the distribution of the signal maxima and minima can be interpreted as the propagation of a large scale wave, yet the origin of this wave calls for further research.
Concluding this chapter we would note an extremely high signal recorded in October 18-19 (Figure 6), that is, two days after the earthquake. This signal did not correlate with the growth of magnetic activity, either, being absent at the northernmost Gabb and Dyer sites (see also Figures 7 and 4a, where magnetic activity decreased in this time period). At the same time, the fairly intensive (M~4.5) aftershocks of October 18 (Figure 4e) might affect the ionosphere by means of the effect of internal gravity waves. Generally, the disturbed region of the ionosphere propagated eastward (Figure 6).
To sum up, the method of an optimum detector allows one to get additional information for the ionospheric disturbances which in this case corresponded to the earthquake time and do not correlate with the growth of geomagnetic activity. It is obvious that this subject calls for a further study.
Kushida and Kushida [[2002] discovered anomalous time variations in the intensity of VLF radio waves (108 MHz) propagating from distant radio stations 4-8 days before the earthquakes that occurred in Japan. These variations were classified into several types of anomalies which were used to locate the epicenter and estimate the magnitude of the impending earthquake.
The most probable physical explanation of these anomalies was offered by Pilipenko et al. [[2001]. Large internal gravity waves that are generated in a seismically active region are believed to be the main factor responsible for the origin of ionospheric disturbances, especially in the Es sporadic layer. This layer can be considered as a source of free energy to generate small-scale ionospheric heterogeneities in the ionospheric plasma. These heterogeneities may cause the VLF wave backscattering.
How can these heterogeneities be discovered using the GPS data? Indeed, the formation of small-scale heterogeneities, causing the scattering of VLF waves [E and Lyu, 1982] (the size of the first Fresnel zone being 600-800 m), implies the intensification of heterogeneities with the growing size of the first zone for GPS signals (in the 150-200-meter range with F being 250-300 m).
In the case of the GPS system, the solution of the navigation problem is based on the measurements of the group and phase delays of the signal, proportional to the TEC values measured along the ray from the source to the receiver, the signal magnitude being measured only for estimating the quality of the data and, hence, being auxiliary. It is only recently that special GPS detectors were manufactured, which allow one to measure the magnitude of the signal with a discretization frequency necessary to record scintillations (below 50 Hz) [Kintner et al., 2001; Ledvina et al., 2002].
Using a receiver of this kind, high GPS signal scintillations were recorded not only in the equatorial zone [Kintner et al., 2001], but also in a middle-latitude area during the moderate magnetic storm of September 25-26, 2001 [Ledvina et al., 2002]. Kintner et al. [[2001] provided a direct proof for a connection between the high amplitude fading of a signal at the main GPS frequency, f1, and the breaking of this signal accompaniment in the time interval when the signal level droped below the noise level; these fadings of the signal were caused by the dissipation at small heterogeneities in the equatorial zone.
Ledvina et al. [[2002] were the first to observe intensive mid-latitude variations in the magnitudes of L1 GPS signals at the latitudes corresponding to the northeast of the USA. This disturbance caused intensive magnitude scintillations ( > 20 dB, the scintillation index being S4=0.8 ) of a decimeter range, which are not characteristic of these latitudes. The parallel TEC measurements showed distinct density gradients (about 30 TECU/deg) and the presence of distinctly expressed irregular structures [Ledvina et al., 2002].
Afraimovich et al. [2004] demonstrated that the failures observed in the GPS system positioning might have been associated with the emergence of high small-scale heterogeneities which cause GPS radiosignal dissipation.
The study of scintillations in the ionosphere is one of the methods for sounding ionospheric irregularities, mainly in the E and F regions [Krein, 1977; E and Lyu, 1982]. The scintillations observed at different frequencies were studied in detail in equatorial and auroral regions of the Earth [Aarons, 1997; Aarons et al., 1996, 1999; E and Lyu, 1982]. It is believed that in contrast to equatorial and auroral regions the mid-latitude regions do not show any large concentration gradients, or intensive electric fields necessary for the development of plasma instabilities which lead to the formation of electron concentration heterogeneities responsible for scintillation formation.
Nevertheless, the experiments carried out in Japan as far back as 1982 at a mid-latitude site with the coordinates of 34o N, 131o E yielded the SI values varying from 2 to 10 dB in the GPS frequency range [Karasawa et al., 1985]. The abnormal fluctuations recorded during 13 months of observation originated mainly during the night time and lasted 5 seconds to 2 minutes.
On the other hand, the indirect confirmation of the hypothesis for the intensive development of a small-scale heterogeneous structure of the ionosphere during the period of earthquake preparation was provided by the results of measuring variations in the Doppler frequency displacement (DFD) of the radio signal reflected from the ionosphere in Ashkhabad [Ovezgeldyev et al., 1988]. The sudden broadening of the spectrum of a signal reflected from the ionosphere during a few dozens of seconds can be used as an indicator of the effect of infrasound noise on the ionosphere and as a precursor of gravity waves produced by earthquakes [Nagorskii, 1979].
Ovezgeldyev et al. [1988] described the results of their observations during an earthquake preparation (a few tens of minutes before the events). The analysis of their experimental data allowed the authors to come to the following conclusions. The preparation periods of some earthquakes (46 events) were marked by the substantial broadening of the DFD spectrum (averaged to 0.73 Hz) and by a significant growth of the DFD dispersion (7-8 times compared to the quiet moments) 10 to 70 minutes before the earthquakes. In the case of many earthquakes the broadening of the spectrum and the growth of the DFD dispersion began a few dozens of minutes before the earthquake and ended just prior to the earthquake onset.
To sum up, one of the methods of monitoring the processes that accompany earthquake preparation can be based on the recording of the magnitude and phase oscillations of GPS signals. In fact, this is a GPS version of monitoring the Kushida effect [Kushida and Kushida, 2002], the only difference being the use of decimeter waves instead of VLF ones.
1. The aim of this paper was to analyze the potential possibility of GPS monitoring for detecting the potential precursors of earthquakes, using the Hector Mine earthquake omit occurred on October 16, 1999, in California, as an example. The choice of this event was dictated by the fact that a dense network of land-based GPS sites was operating at the time of this fairly large earthquake ( M =7.1).
2. Reported in this paper is the detailed analysis of the total electron content over a sufficiently long time interval, including the day of the earthquake (October 13 to 18, 1999), following a somewhat conventional, though useful classification of the main types of the known seismic ionospheric effects: the quasiregular variation of ionospheric parameters and the generation of internal gravity waves.
3. However, the analysis of the TEC variations in the IGW period range suggests that the observed TEC variations seem to be controlled by the local time and even by moderate geomagnetic activity and are not associated with any of the expected processes that accompany the process of earthquake preparation. Further refinement needs data processing.
4. At the same time there are definite prospects for recording the processes of earthquake preparation by detecting small-scale ionospheric heterogeneities which are supposed to arise in the course of earthquake preparation, using the results of the special measurements of GPS signal amplitude and phase scintillations.
Aarons, J., M. Mendillo, E. Kudeki, et al. (1996), GPS phase fluctuations in the equatorial region during the MISETA 1994 campaign, J. Geophys. Res., 101(A12), 26,851-26,861.
Aarons, J. (1997), Global positioning system phase fluctuations at auroral latitudes, J. Geophys. Res., 102(A8), 17,219-17,231.
Aarons, J., and B. Lin (1999), Development of high-latitude phase fluctuations during the January 10, April 10-11, and May 15, 1997 magnetic storms, J. Atmos. Sol. Terr. Phys., 61, 309-327.
Afraimovich, E. L. (2000), The GPS global detection of the ionospheric response to solar flares, Radio Sci., 35(6), 1417-1424.
Afraimovich, E. L., and O. S. Lesyuta (2003), Instantaneous response of mid-latitude ionosphere to the sudden onsets of high magnetic storms, Space Res., 41(2), 120-128.
Afraimovich, E. L., A. I. Terekhov, M. Yu. Udodov, and S. V. Fridman (1992), Refraction distortions of transionospheric radio signals caused by changes in a regular ionosphere and by travelling ionospheric disturbances, J. Atmos. Sol. Terr. Phys., 54, 1013-1020.
Afraimovich, E. L., K. S. Palamartchuk, and N. P. Perevalova (1998), GPS radio interferometry of travelling ionospheric disturbances, J. Atmos. Sol. Terr. Phys., 60, 1205-1223.
Afraimovich, E. L., O. N. Boitman, A. D. Kalikhman, T. G. Pirog, and E. I. Zhovty (1999), Dynamics and anisotropy of travelling ionospheric disturbances as deduced from transionospheric sounding data, Radio Sci., 34, 477-487.
Afraimovich, E. L., E. A. Kosogorov, O. S. Lesyuta, A. F. Yakovets, and I. I. Ushakov (2001a), Geomagnetic control of the spectrum of travelling ionospheric disturbances based on data from a global GPS network, Annales Geophysical, 19(7), 723-731.
Afraimovich, E. L., E. A. Kosogorov, Perevalova, and A. V. Plotnikov (2001b), Comparison of the TEC response of the shock-acoustic waves generated during rocket launchings, by earthquakes, and explosions, Proc. Intern. Beacon Satellite Symposium, June 4-6, pp. 373-377, Boston College, Institute for Scientific Research, Chestnut Hill, MA, USA.
Afraimovich, E. L., N. P. Perevalova, A. V. Plotnikov, and A. M. Uralov (2001c), Shock-acoustic waves generated by earthquakes, Annales Geophysical, 19(7), 395-409.
Afraimovich, E. L., E. A. Kosogorov, A. V. Plotnikov, and A. M. Uralov (2001d), Acoustic shock waves generated by earthquakes, Physics of the Earth, (6), 16-28.
Afraimovich, E. L., V. V. Kiryushkin, and N. P. Perevalova (2002a), The estimation of ionosphere disturbance characteristics in the near zone of an earthquake epicenter, Radio Engineering and Electronics, 47(7), 822-830.
Afraimovich, E. L., E. A. Kosogorov, and A. V. Plotnikov (2002b), Acoustic shock waves generated by rocket launchings and earthquakes, Space Res., 40(3), 383-393.
Afraimovich, E. L., N. P. Perevalova, and S. V. Voyeikov (2003), Travelling wave packets of total electron content disturbances as deduced from global GPS network data, J. Atmos. Sol. Terr. Phys., 65(11-13), 1245-1262.
Afraimovich, E. L., E. I. Astafieva, O. I. Berngardt, V. V. Demiyanov, et al. (2004a), Mid-latitude GPS signal scintillations and malfunctions of GPS functioning at the boundary of an auroral oval, Izv. Vuzov, Radiophizika, in press.
Afraimovich, E. L., E. I. Astafieva, and S. V. Voyeikov (2004b), Isolated ionospheric disturbances as deduced from global GPS network, Annales Geophysical, 22, 47-62.
Alimov, O. A., M. B. Gokhberg, E. V. Liperovskaya, et al. (1989), Abrupt density declines in the Es sporadic layer in the ionosphere as precursors of earthquakes, Doklady AN SSSR, 305(6), 1335-1339.
Astafieva, E. I., E. L. Afraimovich, and A. V. Plotnikov (2002), Search for earthquake precursors in the total electron content of the ionosphere from global GPS data, Proc. XX All-Russia Conference on Radio Wave Propagation, pp. 90-91, Nizhnii Novgorod.
Box, D., and G. Jenkins (1974), Analysis of Time Series, Prediction and Control, 38 pp., Mir, Moscow.
Buchachenko, A. L., V. N. Oraevskii, O. A. Pokhotelov, et al. (1996), Ionospheric precursors of earthquakes, Adv. Phys., 166(9), 1023-1029.
Calais, E., and J. B. Minster (1995), GPS detection of ionospheric perturbations following the January 1994 Northridge earthquake, Geophys. Res. Lett., (22), 1045-1048.
Calais, E., J. B. Minster, M. A. Hofton, and M. A. H. Hedlin (1998a), Ionospheric signature of surface mine blasts from Global Positioning System measurements, Geophys. J. Int., 132, 191-202.
Calais, E., J. B. Minster, and J. Bernard (1998b), GPS, earthquake, ionosphere, and space shuttle, Phys. Earth Planet. Inter., (105), 167-181.
Calais, E, J. S. Haase, and J. B. Minster (2003), Detection of ionospheric perturbations using dense GPS arrays in Southern California, Geophys. Res. Lett., 30(12), 1628, doi:10.1029/2003GL017708.
Davies, K. (1980), Recent progress in satellite radio beacon studies with particular emphasis on the ATS-6 radio beacon experiment, Space Sci. Rev., 25(4), 357-430.
Davies, K., and G. K. Hartmann (1997), Studying the ionosphere with the Global Positioning System, Radio Sci., 32(4), 1695-1703.
Druzhin, G. I. (2002), Experience of predicting earthquakes in Kamchatka from monitoring very low frequency radiation, Volcanology and Seismology, (6), 51-62.
E, Gundze, and Zhaohan Lyu (1982), Radiowave scintillation in the ionosphere, TIIER, 70(4), 5-45.
EQINFO: Preliminary report of the 10/16/1999 M=7.1 Hector Mine, California Earthquake, http://pasadena.wr.usgs. gov/hector/hector-srl.html.
Fitzgerald, T. J. (1997), Observations of total electron content perturbations on GPS signals caused by a ground level explosion, J. Atmos. Sol. Terr. Phys., (59), 829-834.
Gokhberg, M. B., and S. L. Shalimov (2000), The lithosphere and ionosphere relationship and its modeling, Russian J. Earth Sci., 2(2).
Gokhberg, M. B., V. A. Pilipenko, O. A. Pokhotelov, and S. Partasarati (1990), Acoustic disturbance from an underground nuclear explosion as a source of electrostatic turbulence in the magnetosphere, Proc. USSR Academy of Science, 313(3), 568-574.
Gohkberg, M. B., A. K. Nekrasov, and S. L. Shalimov (1996), The effect of unstable greenhouse gas seepage in earthquake-prone regions on the ionosphere, Physics of the Earth, (8), 52-55.
Hines, C. O. (1960), Internal atmospheric gravity waves at ionospheric heights, Can. J. Phys., 38(8), 1441-1481.
Ho, C. M., V. A. Iijima, X. P. Lindqwister, et al. (1998), Ionospheric total electron content perturbations monitored by the GPS global network during two northern hemisphere winter storms, J. Geophys. Res., 103, 26,409-26,420.
Hocke, K., and K. Schlegel (1996), A review of atmospheric gravity waves and travelling ionospheric disturbances: 1982-1995, Annales Geophysical, 14, 917-940.
Hofmann-Wellenhof, B., H. Lichtenegger, and J. Collins (1992), Global Positioning System: Theory and Practice, p. 327, Wien, New York, Springer-Verlag.
Hunsucker, R. D. (1982), Atmospheric gravity waves generated in the high-latitude ionosphere: A review, Rev. Geophys., 20, 293-315.
IONEX: ftp://caddisa.gs f c.nasa.gov/pub/gps/products/ionex
INTERMAGNET: International Real-Time Magnetic Observatory Network, CD of Definitive Geomagnetic Data of 2000, France, 2003: http://www.intermagnet.org
Ivanov-Kholodnyi, G. S., and A. V. Mikhailov (1980), Determinate Approach to Ionospheric Process Prediction, 42 pp., Gidrometoeizdat, Leningrad.
Kashchenko, N. M., S. P. Kshevetskii, A. V. Matsievskii, and M. A. Nikitin (1990), Resonance generation of ionospheric bubbles by internal gravity waves, Geomagnetism and Aeronomy, 30, 446-451.
Karasawa, Y., K. Yasukawa, and M. Yamada (1985), Ionospheric oscillation measurements at 1.5 GHz in mid-latitude region, Radio Sci., 20(3), 643-651.
Kelley, M. C. (1989), The Earth's Ionosphere, in Plasma Physics and Electrodynamics, pp. 485, Academic Publ. Comp., California.
Kintner, P. M., H. Kil, and E. de Paula (2001), Fading time scales associated with GPS signals and potential consequences, Radio Sci., 36(4), 731-743.
Klobuchar, J.A. (1986), Ionospheric time-delay algorithm for single-frequency GPS users, IEEE Trans. Aerosp. Electron. Syst. AES, 23(3), 325-331.
Klobuchar, J. A. (1997), Real-Time Ionospheric Science: The new reality, Radio Sci., 32, 1943-1952.
Kolokolov, L. E., E. V. Liperovskaya, V. A. Liperovskii, et al. (1992), Pronounced spreadings of the sporadic E layers in the middle-latitude ionosphere during earthquake preparation, Physics of the Earth, (7), 101-109.
Krein, R. K. (1977), Radio signal scintillation in the ionosphere, TIIER, 65(2), 5-29.
Kushida, Y. and R. Kushida (2002), Possibility of earthquake forecast by radio observations in the VHF band, J. Atmospheric Electricity, 22(33), 239-255.
Kushnir, A. F., V. M. Laoshin, V. I. Pinsky, and J. Fyen (1990), Statistically optimal detection using small array data, Bull. Seismol. Soc. Am., 80(80), 1934-1950.
Larkina, V. I., A. V. Nalivaiko, N. I. Gershenzon, M. B. Gokhberg, et al. (1983), The "Interkosmos-19'' satellite observation of VLF radiation associated with seismic activity, Geomagnetism and Aeronomy, 23(5), 842-846.
Ledvina, B. M., J. J. Makeda, and P. M. Kintner (2002), First observations of intense GPS L1 amplitude scintillations at midlatitude, Geophys. Res. Lett., 29(14), doi:10.1029/2002GL014770.
Levin, V. E., E. I. Gordeev, V. F. Bakhtiarov, and M. Kasahara (2002), Preliminary results of GPS monitoring in Kamchatka and Komandorskie Islands, Volcanology and Seismology, (1), 3-11.
Linkov, E. M., L. N. Petrova, and D. D. Zuroshvili (1989), Seismogravitational oscillations of the Earth and related atmospheric disturbances, Doklady AN SSSR, 306(2), 314-317.
Liperovskii, V. A., O. A. Alimov, S. L. Shalimov, et al. (1990), The study of the ionospheric F -region before earthquakes, Physics of the Earth, (12), 77-85.
Mannucci, A. J., C. M. Ho, U. J. Lindqwister, et al. (1998), A global mapping technique for GPS-derived ionospheric TEC measurements, Radio Sci., 33, 565-582.
Mercier, C. (1996), Some characteristics of atmospheric gravity waves observed by radio-interferometry, Annales Geophysical, (14), 42-58.
Nagorskii, P. M. (1979), The impact of infrasound noise from minor earthquakes on the spectrum of the radio signal reflected from the ionosphere, Geomagnetism and Aeronomy, 19(1), 68-72.
Oliver, W. L., Y. Otsuka, M. Sato, T. Takami, and S. Fukao (1997), Climatology of F-region gravity wave propagation over the middle and upper atmosphere radar, J. Geophys. Res., 102, 14,449-14,512.
Ondoh, T. (1999), Seismo-ionospheric effects, in Atmospheric and Ionospheric Electromagnetic Phenomena Associated with Earthquakes, edited by M. Hayakawa, pp. 789-803, Tokyo.
Ovezgeldyev, O. G., M. Goshdzhanov, M. B. Mukhanov, et al. (1988), Ionospheric effects of earthquakes proved by Dopler measurements, Izv. AN TSSR, (1), 17-25.
Parrot, M. (1994), Statistical study of ELF/VLF emissions recorded by a low-altitude satellite during seismic events, J. Geophys. Res., 99(12), 23,339-23,347.
Pertsev, N. N., and S. L. Shalimov (1996), Generation of atmospheric gravitational waves in a region of active earthquakes and their effects on the ionosphere, Geomagnetism and Aeronomy, 36, 111-118.
Pilipenko, V., S. Shalimov, S. Uyeda, and H. Tanaka (2001), Possible mechanism of the over-horizon reception of FM radio waves during earthquake preparation period, Proceedings of the Japan Academy, 77(7), ser. B, 125-130.
Pogoreltsev, A. I., and N. N. Pertsev (1995), The effect of phonon wind on the structural formation of acoustic-gravity waves in the thermosphere, Izv. Rus. Akad. Nauk, Physics of the Atmosphere and Ocean, 31(6), 755-760.
Saito, A. M., M. Nishimura, M. Yamamoto, et al. (2001), Traveling ionospheric disturbances detected in the FRONT campaign, Geophys, Res. Lett., (28), 689-692.
Shalimov, S. L. (1992), Lithosphere-ionosphere relationship: A new way to predict earthquakes?, Intern. Geosci. Newsmag. Episodes, 15(4), 252-254.
Somsikov, V. M. (1995), On the mechanism of the formation of atmospheric inhomogeneities in the solar terminator region, J. Atmos. Terr. Phys., (57), 75-83.
SOPAC: Scripps Orbit and Permanent Array Center's website: http://sopac.ucsd.edu/cgi-bin/dbDataByDate.cgi
SPIDR: Space Physics Interactive Data Resource: http://spidr.ngdc.noaa.gov/spidr/index.html
Tsugawa, T., A. Saito, Y. Otsuka, and M. Yamamoto (2003), Damping of large-scale traveling ionospheric disturbances detected with GPS networks during a magnetic storm, J. Geophys. Res., 108(A3), 1127, doi:10.1029/2002JA009433.
USGS: United States Geological Survey's website: http://wwwneic.cr.usgs.gov/neis/bulletin/
Voitov, G. I., and I. P. Dobrovolskii (1994), Chemical and carbon isotope variations of natural gas flows in earthquake-prone regions, Physics of the Earth, (3), 20-31.
WDC: WDC Data, models and other facilities: http://www.wdc.rl.ac.uk/cgi-bin/wdcc1/secure/wdcdata
Wilson, B. D., A. J. Mannucci, and C. D. Edwards (1995), Subdaily northern hemisphere maps using the IGS GPS network, Radio Sci., 30, 639-648.