S. V. Starchenko
Institute of Terrestrial Magnetism, Ionosphere, and Radiowave Propagation, Russian Academy of Sciences, Troitsk, Moscow oblast
Convection in deep interiors of planets [Stevenson et al., 1983] and their natural satellites [Kuskov and Kronrod, 1998] can be due to both thermal and gravitational effects [Loper, 1978]. Only at a certain evolutionary stage of a planet (satellite), can compositional convection, largely controlled by gravitational differentiation of its composition, arise somewhere in its deep liquid interiors. Very vigorous compositional convection should take place, for example, due to the differentiation of the Earth's core into liquid and solid phases. As was described for the first time by Braginsky [Braginsky and Roberts, 1995], such convection is associated with the floating-up of an excessive lighter component from the boundary with a slowly growing inner solid core, a heavier component being precipitated onto this boundary from the contracting outer liquid core.
The growth rate of the Earth's solid core can be estimated by dividing the present-day radius of the core by its age (1-3 Ga), which yields a value of ~10-11 m s-1. The relations governing this rate and the conditions favoring the occurrence of compositional convection have not been explored as yet. Moreover, of the best of our knowledge, even basic criteria of similarity have not been developed for compositional convection in a rapidly and almost rigidly rotating planetary spherical layer [Starchenko, 2000]. Only a few widely known studies (e.g. see [Glatzmaier and Roberts, 1997; Starchenko and Jones, 2002]) were devoted to the direct numerical modeling of magnetic effects due to thermal and compositional convection. The assumptions underlying these studies are so unrealistic and their model time intervals are so limited that their results are by no means usable for developing the theory of compositional convection in a rotating spherical liquid layer.
The goal of this paper is the development of the general theory, as well as its experimental simulation basis, for gravitational differentiation and the related compositional convection in a rapidly and nearly rigidly rotating spherical liquid layer in deep interiors of planets and natural satellites.
The simplest mathematical model describing the main features inherent in the gravitational differentiation of deep interiors of planets and natural satellites is proposed in the second section of this paper. The spherical liquid layer under consideration is assumed to be an adiabatic state with no thermal convection. Moreover, for simplicity, the buoyancy acceleration that can arise in such a layer is assumed to be directed strictly along the radius.
In the third section, it is shown that, given a stationary density determined from seismic observations or evolutionary models, the initial equations for the gravitational potential, pressure, and concentration of the lighter component have a basic analytical solution. This basic solution completely defines the global growth rate of the solid inner sphere and the intensity of the possible compositional convection. Main hydrostatic effects and similarity criteria associated with this slow growth of the solid sphere modeling the inner core of a planet or a natural satellite are described theoretically.
In the fourth section, the convective instability and similarity criteria are considered for compositional convection in a rotating layer. Comparison between chemical and thermal convection patterns made it possible to utilize some results derived for thermal convection. On the other hand, unique effects inherent in compositional convection are established. The main effect is the formation of a concentration boundary layer controlling the freezing-out behavior of the liquid at the surface of the inner sphere. Specific features of this behavior can result in the asymmetry of the Earth's rigid core. The presence of the concentration layer and the effect of rapid rotation can raise significantly the excitation threshold of compositional convection as compared with thermal convection. As a result, the magnetohydrodynamic system driven by the compositional convection is likely to be in the laminar state in the Earth, near the generation threshold in Mercury and beyond the generation threshold in Venus and Mars.
In the final, fifth section, main conclusions are formulated and a project of an experimental installation for the laboratory simulation of gravitational differentiation of deep planetary interiors is discussed.
A simplified mathematical model, discussed below, is primarily developed to reconstruct main effects of the gravitational differentiation in deep liquid interiors of terrestrial planets (Mercury, Venus, the Earth, and Mars), because the dependence of their evolution on gravitational differentiation raises no doubts [Stevenson et al., 1983]. Moreover, the model proposed here is applicable to large natural satellites similar in internal structure to terrestrial planets (for example, the Moon, the Jupiter's satellites Ganymede, Europa, and Callisto [Kuskov and Kronrod, 1998], and other similar satellites of giant planets). Finally, this model can have some implications for Neptune, Uranus, Saturn, and Jupiter, if gravitational differentiation played a substantial role in the formation of inner rigid cores in these planets.
To pinpoint main effects of gravitational differentiation, we address an idealized body in which the following conditions are valid.
(i) The spherical liquid layer under consideration is in the adiabatic state without thermal convection. This condition can be valid even in the Earth's core, where it is still not evident that the adiabatic gradient exceeds the value required for excitation of thermal convection.
(ii) Gravitational differentiation proceeds in the spherical liquid layer (the liquid core) consisting of heavy and light components. The heavy component forms a slowly growing (billions of years in the Earth) inner solid core.
(iii) The buoyancy acceleration is assumed to be strictly radial in a reference frame rotating together with the outer boundary of the liquid core, because the centrifugal acceleration is appreciably smaller than the gravitational acceleration in deep interiors of planets and satellites.
If the mass fraction of the light component (or admixture) x is referred to as the concentration, basic equations describing the simplified model of gravitational differentiation proposed here are (e.g. see [Braginsky and Roberts, 1995; Loper, 1978; Starchenko, 2001])
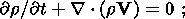 | (1a) |
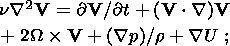 | (1b) |
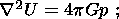 | (1c) |
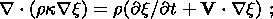 | (1d) |
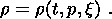 | (1e) |
Here the reference frame rotates at a fixed angular velocity
W close to that of
the rotating outer boundary of the liquid core at
r=r o,
r is density,
t is
time,
The boundary conditions for the velocity in (1a) and (1b) are controlled by the
structure of the outer and inner ( r=r i ) boundaries of the liquid core. At
rigid boundaries in liquid cores of terrestrial planets, these conditions can be
written as
Relation (2b) and the dynamic equation for the relative angular velocity of the
inner rigid boundary, derived from (1a) and (1b), make the system of equations
complete. The gravitation equation (1c) is complemented by the continuity
conditions imposed on the gravitational potential
U and its gradients
In the case of terrestrial planets, equations (1d) and (1e) are complemented by
the outer condition of impermeability, inner condition of diffusion and phase
transition condition at the inner liquid/solid interface:
Here,
r=Ri
The important parameter
St, introduced in (4b), physically means a
characteristic frequency of the thermogravitational differentiation of the core
of a planet (or a satellite) into liquid and solid components. The numerical
value of (4b) specifies, in a natural way, the age (~1/
St ) of the Earth's rigid
core that amounts to about one billion of years.
Thus, at times significantly shorter than 1/
|St|, all of the model relations
presented in this section can be reliably used in the study of gravitational
differentiation. Moreover, with an accuracy sufficient for the model considered,
we can assume below that all external parameters in (4) and (3b, 3c) are constant
in time and space.
In order to successfully solve system (1)-(3), we should specify an initial
condition as simple as possible. In what follows, this state is referred to a
basic state, and all related values have the index "0".
An optimal approach is to choose such a basic state that has a
given stationary radial distribution of density
r0(r) satisfying the model of
internal structure of a planet (satellite)
in a certain epoch. In order to model the basic state of the
Earth's liquid core in the modern epoch, it is natural to take the
density distribution from the PREM seismic model
[Dziewonski and Anderson, 1981].
Ancient epochs can be modeled, for example, with the use of the model proposed in
[Loper, 1978],
which describes the entire differentiation process of the Earth's core
into its solid and liquid parts.
The basic stationary, spherically symmetric density
r0(r) should satisfy
equation of state (1e) with an adequate accuracy over the time interval of the
epoch considered. Evidently, the radial density distribution in the Earth's core
would change by a value on the order of 10% over about one billion years.
Therefore, the characteristic time required for a significant change in the
density is about ten billion years. Accordingly, if an accuracy of the order of
1% is taken for the description of the basic state, the duration of the model
epoch for the Earth will not exceed a value on the order of 100 Myr.
The continuity equation (1a) will be satisfied for the basic state if no
convection is present,
V0=0. The remaining three equations in (1) are
simplified and have the form
Starting from the center, equation (5a) can be easily integrated with respect to
The substitution of this solution into (5b) immediately provides the stationary
pressure gradient.
The general solution of the diffusion equation (5c) satisfying boundary
conditions (3) can be conveniently expressed through the rate of the
concentration increase
x, which is constant in the epoch modeled, and
the
derivative
x
Hence, using (3b) and (3c), we obtain an estimate for the growth rate of
the
solid sphere (~10-11 m s-1 in the Earth):
which is independent of the diffusion coefficient
k.
If the liquid spherical layer cools, its entropy decreases with time and we have
St>0, as in (4b). In this case, the growth rate of the inner
solid sphere (8)
is positive and the concentration gradient is negative, i.e.
x
where
x
The stationary difference of concentration across the liquid layer
Dx or the
relative concentration difference of density is determined by the integration of
(7b):
Given the molecular diffusion coefficient
k
As seen from (9) and (7a), the quantity
Dx
Let the density, gravitational potential, pressure and concentration be
represented as sums of basic (see above) and relatively small convective
components:
r0+r,
U0+U,
p0+p and
x0+x,
respectively. Then,
taking into account equations (5)-(7), describing the initial state, can be
rewritten in the following, "convective'' form:
The quantities
r
Using (10e) and (5)-(7), the bracketed terms in (11b) and (11c) can be
transformed into a form advantageous for their further effective application.
First, we write separately the buoyancy acceleration from (11b):
The bracketed term in (11c) can then be transformed to the form
It is evident from this relation and from (9) that the value (12b) is
Dx times smaller
than the first term on the left-hand side of (11c),
which is usually minimal in a larger part of the liquid layer. Hence, since
Dx
Finally, introducing the effective pressure
P
Here,
g0(r)
The system of 8th order (13) is complemented by six boundary conditions (2) for
the vector
Here,
r i = r i0 + r i t
is the radius of the solid sphere, linearly varying with time;
r i = const is determined in (8); and
r i0 = const is the initial radius at the time
moment
t = 0, when the system under consideration is adequately described by
the spherically symmetric basic state (see the preceding section). The remaining
parameters in (14b) are determined in (3b, 3c) and (4a, 4c).
Boundary condition (14b) differs essentially from all boundary
conditions known studies of thermal convection, which is usually
examined in the Boussinesq approximation
(e.g. see [Braginsky and Roberts, 1995;
Starchenko, 2000]).
Due to (14b), compositional convection inevitably
involves the presence of a specific inner boundary layer that
controls the freezing dynamics of liquid at the boundary of the
inner sphere. Since the convection inevitably becomes asymmetric
after a sufficiently long time interval, the shape of the inner
core should eventually deviate, on a significant level, from a
spherically symmetric shape. This provides a fairly simple
explanation to the asymmetry of the Earth's inner core established
from seismological data.
The thickness of the unique concentration layer
Dr = kXr o/(Fr i V
which amounts to ~10-7 for the value
V
As distinct from the widely known Boussinesq convection, the compositional
convection under study involves a similarity criterion for (13a) characterizing
the stratification of density:
This effect, albeit small in the Earth's core ( d
Unlike (15) and (16), many other numbers characterizing similarity criteria of
compositional convection are either analogous to or coincide with well-known
numbers of thermal convection. Thus, rapid and nearly rigid rotation of liquid
interiors of a planet (or a satellite) is characterized, respectively, by the
Ekman number
E and the Rossby number
e:
It is evident from this definition that these numbers are the same for
both
thermal and compositional convection. The lower bound
e
The lower bound
E
To estimate numerically the intensity of compositional convection sources, we
determine rotational ( E
where
g
To initiate convection, it is necessary that
C exceed a certain critical value
C cr. In the case of thermal convection, if
R exceeds the critical Rayleigh
number
R cr
The system is at the convection excitation threshold if the time derivatives of
the relative concentration and velocity are close to zero in (13b, 13c):
|x-1
Given the relative thickness
d
Presently, the intensity of compositional convection is close
to its maximum, as
is evident from Figure 2. On the contrary, in the distant past, when the Earth's
solid core was small enough, compositional convection was not so intense. There
even existed a critical radius of the solid core starting from which the
convection was excited. The convection will start attenuating beginning from a
certain time moment in future and will stop at the second critical radius, when
the thickness of the liquid layer becomes too small, as is seen from Figure 2. It
is quite probable that presently the radius of the radius of the solid core
exceeds the second critical value in Mars and has not attained the first
critical value in Venus. This is a likely reason why these planets do not have
own significant magnetic fields. Even if compositional convection exists in the
interiors of Mercury, its intensity is nearly critical because the own magnetic
field of the planet is very weak and irregular.
Our project of an experimental installation is largely similar to that described
in
[Sumita and Olson, 1999]
and already used for modeling thermal convection. Therefore, below we do
not go into technical detail but focus on significant distinctions from the
model proposed in
[Sumita and Olson, 1999]
that are beneficial to the effective use of the
installation proposed here primarily for modeling compositional convection and the
related differential rotation. Evidently, this installation is also applicable
to the modeling of thermal and combined convection in deep interiors of planets.
An important element of the experimental installation is a
light and transparent
cap that has the shape of a thin disk and bounds the liquid layer surface from
above (see Figure 3).
The cap both retains the inner hemisphere at the center and
prevents the free surface from buckling due to the rapid rotation. The cap
material should make its viscous coupling with the layer liquid as small as
possible. At the cap boundaries with the hemispheres, it is advantageous to
place light bearings rigidly connected with the hemispheres. Then, the angular
rotation velocity of the cap can be used for estimating the average angular
velocity of the spherical layer.
Note that the laboratory field of the centrifugal and gravitational buoyancy is
opposite in direction to the planetary field modeled. Therefore, in order to
reproduce real effects, the laboratory gradients of temperature and
concentration should be opposite to counterparts in planets. Thus, the radius of
the inner hemisphere, colder than the outer one, should decrease in the
laboratory experiment in order to adequately model hydrodynamic effects
associated with growing hotter solid cores of planets.
Now we estimate the angular velocities of the hemispheres providing the best fit
of the spherically symmetric (radial) field of gravitational buoyancy and the
slightly differential rotation of a liquid core.
The angular velocity of the outer hemisphere is fixed in the
laboratory
experiment (i.e.
W = const in Figure 3) in order to model the rotation of the
outer planetary mantle, whose moment of inertia is much larger than that of the
liquid layer. This value of
W and the gravitational acceleration
g = 9.8 m s-2 determine the equipotential lines of the acceleration field
modeling the gravitation in the interiors of planets
and natural satellites in
the rotating reference frame ( r, q, j )
shown in Figure 3.
The closer the
equipotential lines (21) to the contours
r = const, the better the reproduction
of the radial gravitational field of a planet. An adequate reproduction of this
field is particularly important, because all of the main processes controlling
the compositional convection occur tight here. In this respect, the main line of
family (21) that is tangent to the line
r=r i at
z=r cos q=r i
and
ensures such a reproduction is determined by the criterion of closeness to
r = const
reducing to the minimization of the area bounded by these lines and the
axis
s=r sin q. It is easy to prove that
the absolute minimum of this area is
attained at an angular velocity close to the value
Hence, we obtain that, for example, at
r i = 0.35 m the outer hemisphere should
make one revolution per second for the best possible reproduction of the radial
field of concentration buoyancy near the solid core of a planet.
The angular velocity of the inner hemisphere ( W + w i in Figure 3) should
be
slightly different from that of the outer hemisphere in order to model a
slightly differential rotation in planetary cores. Thus, the reproduction of the
differential rotation in the Earth's core requires that the condition
0
To sum up, we present the main results of this work.
(1) Under assumptions natural for terrestrial planets, a fully analytical
description is obtained for basic hydrostatic effects that control slow growth
of an inner solid core in a planet, gravitational stratification of the liquid
core and the associated sources of compositional convection.
(2) A system of equations governing the virtually unexplored compositional
convection is derived. Main similarity criteria the observance of which is a
prerequisite for successful laboratory simulation of such planetary convection
are substantiated.
(3) New similarity criteria, discovered in this study, characterize the initial
concentration contrast ( Dx
(4) The study showed for the first time that the excitation threshold of
compositional convection should be considerably higher than that of thermal
convection. Therefore, convection in deep interiors of planets and natural
satellites can be nearly laminar in spite of very large values of the
concentration number
C(
(5) The observed planetary magnetic fields yield evidence that a system driven
by compositional convection can be in a laminar regime in the Earth, near the
excitation threshold in Mercury and beyond the excitation threshold in Venus and
Mars.
Braginsky, S. I., and P. H. Roberts, Equations governing convection in the
Earth's core and the geodynamo, Geophys. Astrophys. Fluid Dynamics, 79, 1-97,
1995.
Busse, F. H., Thermal instabilities in rapidly rotating system, J. Fluid Mech.,
44, 441-460, 1970.
Dziewonski, A. M., and D. L. Anderson, Preliminary reference Earth model,
Phys. Earth Planet. Inter., 25, 297-356, 1981.
Glatzmaier, G. A., and P. H. Roberts, Simulating the geodynamo, Contemporary
Physics, 38, (4), 269-288, 1997.
Jones, C. A., A. M. Soward, and A. I. Mussa, The onset of thermal convection
in rapidly rotating sphere, J. Fluid Mech., 405, 157-159, 2000.
Kuskov, O. L., and V. A. Kronrod, Internal structure models of the Jupiter's
satellites Ganymede, Europa and Callisto (in Russian), Astron. Vestnik, 32,
(1), 49-57, 1998.
Lister, J. R., and B. A. Buffett, The strength and efficiency of thermal
and compositional convection in the geodynamo, Phys. Earth Planet. Inter., 91,
17-30, 1995.
Loper, D. E., The gravitationally powered dynamo, Geophys. J. R. Astron. Soc.,
54, 389-404, 1978.
Starchenko, S. V., Supercritical magneto-convection in rapidly rotating
planetary cores, Phys. Earth Planet. Inter., 117, (1-4), 225-235,
2000.
Starchenko, S. V., Anelastic planetary magnetohydrodynamics, NATO Science Series
II: Mathematics, Physics and Chemistry, 26, 217-224, 2001.
Starchenko, S. V., and C. A. Jones, Typical velocities and magnetic field
strengths in planetary interiors, Icarus, 157, 426-435, 2002.
Stevenson, D. J., S. Tilman, and G. Schubert, Magnetism and thermal
evolution of the terrestrial planets, Icarus, 54, 466-489, 1983.
Sumita, I., and P. Olson, A laboratory model for convection in Earth's core
driven by thermally heterogeneous mantle, Science, 286, 1547-1549,
1999.
Wijs, G. A., et al., The viscosity of liquid iron at the physical
conditions of the Earth's core, Nature, 392, 805-807, 1998.
 10-11 m3/(kg cm2 )
is the gravitation constant, and
k is the kinematic diffusion
coefficient of the light admixture. System (1) consists of the continuity (1a),
hydrodynamic (Navier-Stokes) (1b), gravitation (1c), and diffusion (1d)
equations and the equation of state (1e); the latter involves condition (i),
which formally implies that the specific entropy
S is uniform (
10-11 m3/(kg cm2 )
is the gravitation constant, and
k is the kinematic diffusion
coefficient of the light admixture. System (1) consists of the continuity (1a),
hydrodynamic (Navier-Stokes) (1b), gravitation (1c), and diffusion (1d)
equations and the equation of state (1e); the latter involves condition (i),
which formally implies that the specific entropy
S is uniform (  S = 0 ) and
depends only on time:
S = S(t).
S = 0 ) and
depends only on time:
S = S(t). 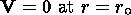
(2a) 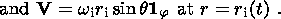
(2b) 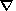 U.
U. 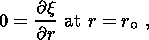
(3a) 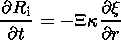
(3b) 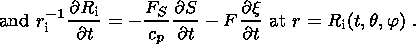
(3c) 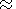 ri
describes a spherically slightly asymmetric surface of
the solid core;
X is the boundary ratio of the density of the
liquid layer to
the density jump at the surface of the solid sphere, providing a change in the
concentration of the light admixture in the liquid;
cp is the specific heat at
constant pressure; and
FS and
F are positive factors controlling the
thermodynamics of freezing and crystallization of the outer liquid core at the
solid core surface. Taking into account the estimates presented in
[Braginsky and Roberts, 1995;
Lister and Buffett, 1995;
Loper, 1978;
Starchenko and Jones, 2002]
for the Earth's core, we have
ri
describes a spherically slightly asymmetric surface of
the solid core;
X is the boundary ratio of the density of the
liquid layer to
the density jump at the surface of the solid sphere, providing a change in the
concentration of the light admixture in the liquid;
cp is the specific heat at
constant pressure; and
FS and
F are positive factors controlling the
thermodynamics of freezing and crystallization of the outer liquid core at the
solid core surface. Taking into account the estimates presented in
[Braginsky and Roberts, 1995;
Lister and Buffett, 1995;
Loper, 1978;
Starchenko and Jones, 2002]
for the Earth's core, we have
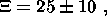
(4a) 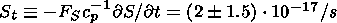
(4b) 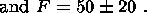
(4c) 3. Basic Hydrostatic State
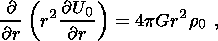
(5a) 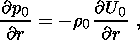
(5b) 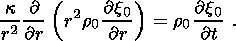
(5c) 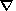 U0 = (
U0 = ( U0/
U0/ r)
1r, because the basic density is specified everywhere
throughout the epoch under consideration:
r)
1r, because the basic density is specified everywhere
throughout the epoch under consideration:
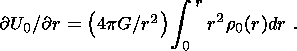
(6)  ,
which depends on the radius
r alone. Using the value
x00, which
is constant in the given epoch and is determined by the equation of state (1e),
this general solution for the initial concentration is written in the form
,
which depends on the radius
r alone. Using the value
x00, which
is constant in the given epoch and is determined by the equation of state (1e),
this general solution for the initial concentration is written in the form
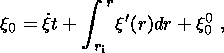
(7a) 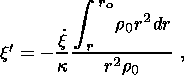
(7b) 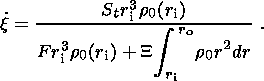
(7c) 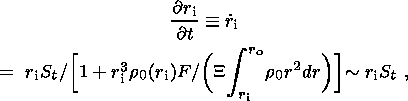
(8)  <0
in (7b). The
corresponding basic hydrostatic state described by the stationary quantities
r0,
<0
in (7b). The
corresponding basic hydrostatic state described by the stationary quantities
r0,  U0,
U0,  p0,
x
p0,
x (r)
and
x = const is generally unstable.
Therefore, given a positive growth rate of the inner sphere, even very small deviations
from such a
basic state with cooling can excite convection (for details, see below). Vice
versa, if the liquid in the layer is heated,
St<0, the inner radius of the
layer decreases and the basic state (5)-(8) is stable with respect to any
arbitrarily small perturbations.
(r)
and
x = const is generally unstable.
Therefore, given a positive growth rate of the inner sphere, even very small deviations
from such a
basic state with cooling can excite convection (for details, see below). Vice
versa, if the liquid in the layer is heated,
St<0, the inner radius of the
layer decreases and the basic state (5)-(8) is stable with respect to any
arbitrarily small perturbations.
Basic state (7) and its energy characteristics
[Lister and Buffett, 1995;
Starchenko and Jones, 2002]
are fully determined by the time derivative of concentration (7c). Considering that
the density in
liquid cores of terrestrial planets varies insignificantly
( Dr0/r0
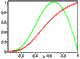
Figure 1
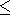 10%),
this
derivative can be approximated, within a reasonable accuracy, by the value
10%),
this
derivative can be approximated, within a reasonable accuracy, by the value
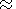 (St/F)/[1
+ (X/F)(x-3 - 1)/3],
(St/F)/[1
+ (X/F)(x-3 - 1)/3],  r i/ro
is the ratio of the inner radius to the outer radius. Figure 1
plots the function
1/[1 + (X/F)(x-3 - 1)/3]
for the Earth, and very similar behavior of this function
should be expected for the other terrestrial planets. Thus, the specific energy
density of gravitational differentiation, which is directly
proportional to
(7c), is negligibly small for
x
r i/ro
is the ratio of the inner radius to the outer radius. Figure 1
plots the function
1/[1 + (X/F)(x-3 - 1)/3]
for the Earth, and very similar behavior of this function
should be expected for the other terrestrial planets. Thus, the specific energy
density of gravitational differentiation, which is directly
proportional to
(7c), is negligibly small for
x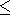 0.1 and subsequently starts rising. The
total
energy of gravitational differentiation is found through multiplying (7c) by the
volume of the liquid layer and vanishes at
x = 1, as is seen from Figure 1.
0.1 and subsequently starts rising. The
total
energy of gravitational differentiation is found through multiplying (7c) by the
volume of the liquid layer and vanishes at
x = 1, as is seen from Figure 1.
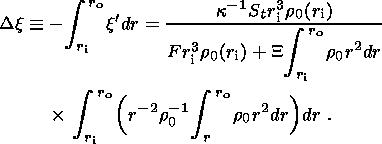
(9) 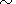 10-5 m2 s-1
generally accepted for
the Earth's liquid core, the value (9) is on the order of 10-1 in the modern
epoch.
10-5 m2 s-1
generally accepted for
the Earth's liquid core, the value (9) is on the order of 10-1 in the modern
epoch.
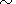 x0 is actually a characteristic
of
the light admixture concentration. In the modern epoch, the same estimate of the
order of 10
-1 was independently obtained for this concentration in the Earth in
[Braginsky and Roberts, 1995;
Lister and Buffett, 1995;
Loper, 1978;
Starchenko and Jones, 2002].
Therefore, all of the values and estimates used in this paper are self-consistent.
x0 is actually a characteristic
of
the light admixture concentration. In the modern epoch, the same estimate of the
order of 10
-1 was independently obtained for this concentration in the Earth in
[Braginsky and Roberts, 1995;
Lister and Buffett, 1995;
Loper, 1978;
Starchenko and Jones, 2002].
Therefore, all of the values and estimates used in this paper are self-consistent.
4. Descripition of the Gravitational Convection
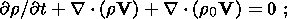
(10a) 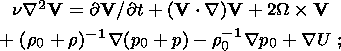
(10b) 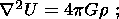
(10c) 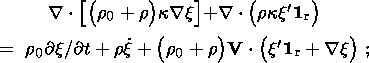
(10d) 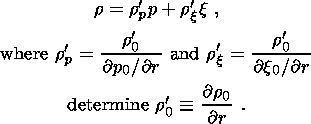
(10e)  p,
and
r
p,
and
r x(r) in (10e) are functions defined through
the basic density
r0(r). In addition, we used relations
derived for planets
from numerical and laboratory simulations:
r0
x(r) in (10e) are functions defined through
the basic density
r0(r). In addition, we used relations
derived for planets
from numerical and laboratory simulations:
r0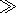 |r|, |p0|
|r|, |p0|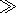 |p| and
x0
|p| and
x0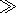 |x|. Based on
these relations and the estimate
|
|x|. Based on
these relations and the estimate
|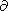 /
/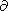 t|
t| | V
| V 
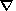 |, typical of convection, the exact
equations (10a)-(10c) can be reduced to a simplified system:
|, typical of convection, the exact
equations (10a)-(10c) can be reduced to a simplified system:
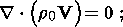
(11a) 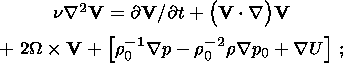
(11b) 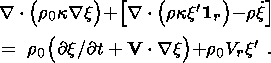
(11c) 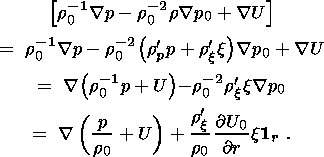
(12b) 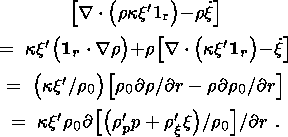
(12b)  1 in the case studied, the contribution of (12b) to (11c) can be neglected
in
the models considered here.
1 in the case studied, the contribution of (12b) to (11c) can be neglected
in
the models considered here.
 r-10
p+U from (12a), we obtain
the simplest convective system of equations
r-10
p+U from (12a), we obtain
the simplest convective system of equations
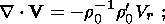
(13a) 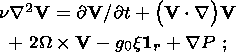
(13b) 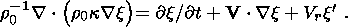
(13c)  -(r
-(r x/r0)
x/r0)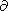 U0/
U0/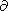 r is the gravitational
acceleration determined from (6) and (10e),
which is responsible for the concentration buoyancy. This acceleration is
directly proportional to ordinary gravitational acceleration
r is the gravitational
acceleration determined from (6) and (10e),
which is responsible for the concentration buoyancy. This acceleration is
directly proportional to ordinary gravitational acceleration
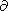 U0/
U0/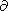 r, with the
proportionality factor
r
r, with the
proportionality factor
r x/r0
amounting to ~0.6 in the Earth
[Braginsky and Roberts, 1995].
The convection intensity is controlled by the product of
g0 and the stationary concentration
gradient
-x
x/r0
amounting to ~0.6 in the Earth
[Braginsky and Roberts, 1995].
The convection intensity is controlled by the product of
g0 and the stationary concentration
gradient
-x given by (7).
given by (7).
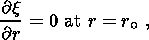
(14a) 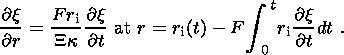
(14b) 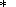 ) is estimated by balancing typical values and
using as a characteristic time the ratio of the
outer size
r o of the system to the characteristic velocity
V
) is estimated by balancing typical values and
using as a characteristic time the ratio of the
outer size
r o of the system to the characteristic velocity
V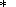 . The
corresponding similarity criterion is described by the number
. The
corresponding similarity criterion is described by the number
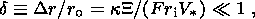
(15) 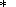 = 10-4 m s-1,
molecular diffusion and
the parameters considered above.
= 10-4 m s-1,
molecular diffusion and
the parameters considered above.
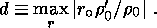
(16) 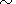 10-1 )
[Dziewonski and Anderson, 1981],
can be significant for convection and magnetism
[Braginsky and Roberts, 1995;
Starchenko, 2001].
10-1 )
[Dziewonski and Anderson, 1981],
can be significant for convection and magnetism
[Braginsky and Roberts, 1995;
Starchenko, 2001].
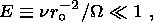
(17a) 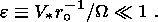
(17b) 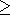 10-6
for the Rossby
number is determined reasonably well from long-term geomagnetic and present-day
seismic observations
[Glatzmaier and Roberts, 1997].
10-6
for the Rossby
number is determined reasonably well from long-term geomagnetic and present-day
seismic observations
[Glatzmaier and Roberts, 1997].
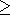 10-15 for the Ekman number is
determined from the iron
value of the molecular viscosity
n
10-15 for the Ekman number is
determined from the iron
value of the molecular viscosity
n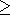 10-6 m2 s-1,
obtained under conditions
typical of the Earth's liquid core
[Wijs et al., 1998].
If the actual value of viscosity is close to this lower bound, the relative thickness
of the
Ekman viscous boundary layer
E1/2
10-6 m2 s-1,
obtained under conditions
typical of the Earth's liquid core
[Wijs et al., 1998].
If the actual value of viscosity is close to this lower bound, the relative thickness
of the
Ekman viscous boundary layer
E1/2 10-7 virtually
coincides with the thickness of the concentration
layer
d from (15). As demonstrated below, such a coincidence
is unlikely to be
accidental. Then, setting
E1/2 equal to
d, we obtain a simple estimate for
the concentration velocity:
10-7 virtually
coincides with the thickness of the concentration
layer
d from (15). As demonstrated below, such a coincidence
is unlikely to be
accidental. Then, setting
E1/2 equal to
d, we obtain a simple estimate for
the concentration velocity:
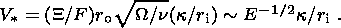
(18)
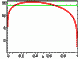
Figure 2
 1 ) concentration number
C. To do this, we utilize
the rotational Rayleigh number
R known in thermal convection (e.g. see
[Starchenko, 2000]).
Replacing in the
R definition the thermal density drop
aDT by
the
analogous value
Dx from (9),
we obtain
1 ) concentration number
C. To do this, we utilize
the rotational Rayleigh number
R known in thermal convection (e.g. see
[Starchenko, 2000]).
Replacing in the
R definition the thermal density drop
aDT by
the
analogous value
Dx from (9),
we obtain
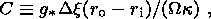
(19) 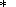 is the characteristic gravitational
acceleration and the layer
thickness
r o-r i is used as the characteristic size.
Concentration number
(19) is fairly large ( C
is the characteristic gravitational
acceleration and the layer
thickness
r o-r i is used as the characteristic size.
Concentration number
(19) is fairly large ( C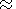 2
2 1015 )
if the following values, typical of the
contemporary liquid core of the Earth are accepted:
Dx
1015 )
if the following values, typical of the
contemporary liquid core of the Earth are accepted:
Dx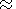 10-1,
k
10-1,
k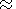 10-5 m2 s-1,
W=7
10-5 m2 s-1,
W=7 10-5 s
-1,
r o-r i=2
10-5 s
-1,
r o-r i=2 106
m
and
g
106
m
and
g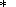
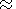 7 m s-2. The
C value is plotted in Figure 2 as a function of the
relative radius of the inner solid core
x
7 m s-2. The
C value is plotted in Figure 2 as a function of the
relative radius of the inner solid core
x r i/ro.
r i/ro. 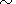 E-1/3
E-1/3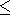 105, sharply asymmetric convection with periods
t
105, sharply asymmetric convection with periods
t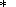
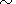 E2/3 r2 o/n
arises
[Busse, 1970;
Jones et al., 2000].
In the Earth's core, this corresponds to the typical velocity
V
E2/3 r2 o/n
arises
[Busse, 1970;
Jones et al., 2000].
In the Earth's core, this corresponds to the typical velocity
V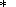 =r o/t
=r o/t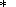
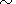 10-3 m s-1.
If the preferable excitation of convection of the same type
were possible in the concentration system considered here, this would lead to
the formation of an overly narrow concentration boundary layer ( d
10-3 m s-1.
If the preferable excitation of convection of the same type
were possible in the concentration system considered here, this would lead to
the formation of an overly narrow concentration boundary layer ( d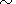 10-8 )
in
accordance with (15). We show that the existence of even much wider layer would
require an incomparably larger value of the critical number and an essentially
different convection pattern.
10-8 )
in
accordance with (15). We show that the existence of even much wider layer would
require an incomparably larger value of the critical number and an essentially
different convection pattern.
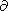 x/
x/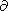 t|
t|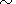 0 and
|V-1
0 and
|V-1 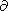 V/
V/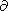 t|
t|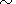 0.
In this case on the strength of (2b), the radial velocity in the
concentration boundary layer (15) has a characteristic value of about
dV
0.
In this case on the strength of (2b), the radial velocity in the
concentration boundary layer (15) has a characteristic value of about
dV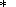 .
The characteristic values
|Vr x
.
The characteristic values
|Vr x |
|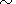 dV
dV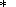 Dx/r
o and
g
Dx/r
o and
g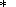 x
x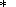 of the "generating'' terms in (13b, 13c) should
be
close to the respective values
kx
of the "generating'' terms in (13b, 13c) should
be
close to the respective values
kx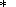 /(r od)2
and
n(dV
/(r od)2
and
n(dV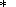 )/(r od)2
for the diffusive and viscous terms hindering the generation. According to definition
(19), this
yields at
r o
)/(r od)2
for the diffusive and viscous terms hindering the generation. According to definition
(19), this
yields at
r o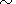 (r o-ri)
an estimate for the largest possible value of the
critical concentration number, expressed through the thickness of the
concentration boundary layer:
(r o-ri)
an estimate for the largest possible value of the
critical concentration number, expressed through the thickness of the
concentration boundary layer:
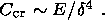
(20) 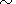 10-7
typical of the Earth and
E = d2,
we obtain
C cr
10-7
typical of the Earth and
E = d2,
we obtain
C cr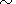 1014, which is
only a little smaller than the contemporary
concentration number
C according to Figure 2. Therefore, compositional convection
can be laminar. This is an entirely new fact, because previously, by analogy
with asymmetric thermal convection
[Braginsky and Roberts, 1995;
Lister and Buffett, 1995;
Starchenko, 2000],
such chemical (or gravitational) convection was always supposed to have an essentially
nonlinear, turbulent and
complicated pattern. The structure of compositional convection should also be
simpler than that of thermal convection, because it is controlled by a more
symmetric concentration boundary layer, which should be related to well-studied
viscous boundary layers.
1014, which is
only a little smaller than the contemporary
concentration number
C according to Figure 2. Therefore, compositional convection
can be laminar. This is an entirely new fact, because previously, by analogy
with asymmetric thermal convection
[Braginsky and Roberts, 1995;
Lister and Buffett, 1995;
Starchenko, 2000],
such chemical (or gravitational) convection was always supposed to have an essentially
nonlinear, turbulent and
complicated pattern. The structure of compositional convection should also be
simpler than that of thermal convection, because it is controlled by a more
symmetric concentration boundary layer, which should be related to well-studied
viscous boundary layers.
5. Project of an Experiment and Conclusions
Figure 3 schematically illustrates the layout of the experimental
installation
modeling the heat-and-mass transfer under conditions typical of planetary deep
interiors. We replaced spheres by hemispheres for the following reasons. First,
the combined centrifugal and gravitational field is capable of reproducing the
equatorial symmetry of the planetary gravitational field, whereas spheres
virtually cannot ensure such a symmetry of this buoyancy field under laboratory
conditions. Second, the central hemisphere can actually float, like a solid
planetary core at the center of the spherical liquid layer. Finally, the use of
hemispheres instead of spheres considerably facilitates effective monitoring and
needed measurements.
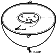
Figure 3
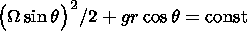
(21) 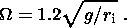
(22) 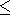 w i/W
w i/W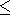 10-5 be valid
[Glatzmaier and Roberts, 1997].
The measurement of such small differences between angular
velocities will require high-precision instrumentation such as layer-scanning
laser illumination and interferometers.
10-5 be valid
[Glatzmaier and Roberts, 1997].
The measurement of such small differences between angular
velocities will require high-precision instrumentation such as layer-scanning
laser illumination and interferometers.
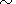 0.1 for the Earth), the compressibility of the
liquid core ( d
0.1 for the Earth), the compressibility of the
liquid core ( d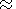 0.1 for the Earth) and the relative
thickness of a
concentration boundary layer ( d
0.1 for the Earth) and the relative
thickness of a
concentration boundary layer ( d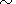 10-7
for the Earth) that, controlling the
liquid freezing process, can also determine the asymmetry of the planetary solid
core.
10-7
for the Earth) that, controlling the
liquid freezing process, can also determine the asymmetry of the planetary solid
core.
 1015 in the Earth), which
is similar to the
rotational Rayleigh number
R.
1015 in the Earth), which
is similar to the
rotational Rayleigh number
R. Acknowledgments
I am grateful to Prof. V. P. Trubitsyn for helpful comments beneficial
to the
improvement of this work. I also thank professors F. H. Busse, A. M. Soward
and
C. A. Jones for fruitful discussions that contributed to the development
of main
ideas underlying this study. The work was supported by INTAS grant no. 99-00348
and by the Russian Foundation for Basic Research, project nos. 03-05-64656 and
02-05-64888.
References
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.1.3) on January 20, 2004.