Russian Journal of Earth Sciences
Vol. 5, No. 4, August 2003
Methods and results of application of the neutron diffractometry
in the
Earth sciences: A Review
A. N. Nikitin and T. I. Ivankina
Frank Laboratory of Neutron Physics, Joint Institute of
Nuclear Research, Dubna, Moscow Region
Contents
Abstract
Fundamental advantages of the neutron methods, that are based on the phenomenal
properties of the neutron allow to extend the number of problems to be resolved in
the solid-state
physics, in geology and in geophysics, are analyzed in detail. A definition is given
in the review
to the crystallographic textures and emphasis was placed on the fact that the preferred
orientation
of the crystal lattices of the rock forming minerals as one of the main factors that
controls the
rock anisotropy, is an inherited property, acquired as a result of magmatism and
metamorphism
and other processes that governed the Earth's lithosphere formation. New results
of investigation
of the rock textural regularities and hence peculiarities of physical properties,
such as behavior
and anisotropy of the elastic wave velocities at high hydrostatic pressures, piezoelectric
properties of some rocks as well as magnetic and thermal properties, are described.
The review
shows examples of application of the neutronography data along with other physical
and
petrophysical methods used to resolve fundamental problems in geology and in geophysics,
such
as reconstruction of the deformations and strains in the lithosphere and studies
of the
metamorphic, geodynamic and evolutionary processes addressed to data on structures
of the
deep-seated samples (xenoliths, amphibolites and gneiss taken from superdeep boreholes).
Results of investigation of abnormal properties of some rocks which appear at a high
temperature and pressure and possibilities of their application for the physics of
destruction and
for development of the earthquake models are discussed.
Introduction
The neutrons came into use in different spheres of natural sciences as well as in
the Earth
sciences shortly after they were discovered.
Differences of minerals and rocks as regards the
g -ray properties, activation characteristics
of their nuclei and peculiar features of interaction with the neutron radiation,
make a physical
basis of the nuclear geophysics methods and serve as a prerequisite for creation
of new methods
for investigation of a composition of the geological materials and the mining and
geological
objects
[Nuclear geophysics, 1961].
In 1936 Heveshi and Levi proposed a nuclear physics method for determining the
substance composition, that was based on activation of the atomic nuclei and on investigation
of
the radioactive radiation occurring due to a variation of the nuclonic composition
or of the
energy state of the nuclei.
The neutron activation analysis has gained a wide acceptance in the world and it
serves for
identification and for a quantitative assessment of the amount of different elements
in the
samples of minerals, ores, soils in water and in air. The activation analysis is
most effectively
used in determining content of noble less-common metals and non-ferrous metals, when
ores
and their after-products having a complicated chemical composition are analyzed
[Activation analysis..., 1967;
Neutron-activation analysis, 1966;
Steinnes, 1977;
Vaganov, 1981].
Pontecorvo, one of the closest collaborators of Fermi in the Roman University, after
his
arrival to the USA, where he became a Head of the geological department, proposed
and
introduced into practice in 1940 a new and an effective method of the oil and gas
prospecting - a
neutron logging
[Pontecorvo, 1941].
At the present time, geological services in many countries make a wide use of different
modifications of the neutron logging: a neutron
g -ray logging, a neutron-neutron logging, a
neutron logging on thermal and fast neutrons, a pulsed neutron logging.
The neutron logging based on the neutron-flux density measurements in a well even
now
is used for the geophysical investigation of the exploratory and production wells,
for
distinguishing the ore seams and for finding out their content of the neutron strong
absorbing
elements, for a lithologic separation and correlation of sections
[Flerov, 1960].
Studies of different types of the neutron scattering in the condensed matter aimed
at
investigation of their structure are given a general term - neutronography
[Nozik et al., 1979;
Ozerov, 1997].
Problems that are solved with the use of the neutronography are similar in many
respects to those that are solved with the help of a well developed and a more readily
X-ray
diffraction. The use of neutrons, however, brings radically new possibilities, that
are quite unique
at times and that are beyond the rich of the X-ray beams.
Fundamental advantages of the neutron methods, that are based on the phenomenal
properties of the neutron allow to extend the number of problems to be resolved in
the condensed
matter physics.
Length of the thermal neutron wave corresponds to typical interatomic distances in
solid
bodies. This feature of the thermal neutrons makes it possible to investigate the
structure and
texture of solid bodies, minerals and the mineral associations and their variations
due to an
external influence.
Progress in the structural and magnetic neutron diffraction, in the neutron spectroscopy
and reflectometry are well known. Application of the scattering neutrons helped to
resolve many
fundamental and applied problems in the physics of the condensed matter in chemistry,
biology,
medicine and in the materials science and in the Earth sciences
[Aksenov, 2000].
A new approach to the neutron diffraction texture analysis that is used along with
some
other physical methods for investigation of the geological properties of materials
for the purpose
of resolving fundamental problems in geology and geophysics has appeared in the last
decade
[Sobolev and Nikitin, 2001].
This review covers major achievements in the Earth sciences that were attained with
the
use of the neutron diffraction analysis.
I. Textures of Geological Materials and the Neutron
Diffraction
Texture Analysis
1.1. Crystallographic Textures and Shape of Rocks
A term "texture'' is widely used in geology. The same term can be met in the
metallophysics and in the material science. As to geologists, they traditionally
understand that
textures mean a wide class of terrestrial formations, for example, geological objects
of different
scale ordered in a different way and ordered heterogeneities, that have certain elements
of
symmetry. According to the scale, different ranks of texture are distinguished, which
differ in
the spatial characteristics and in the time of formation. Thus, layers of a concentrically
anisotropic structure of the Earth's crust are the most large-scale textural elements
of lithosphere.
These form a sedimentary-volcanogenic, granite-metamorphic and other layers. Alternation
of
strata textures (made up of packets, layers) connected with alternation of rocks
of different
genesis are well represented in the crystalline masses. The systems of small fractures,
hierarchy
of parallel cracks, columnar structures like the basalt organs etc. are less frequently
occur.
Two major types of textures can be distinguished in the minerals forming the rocks.
These
are a crystallographic texture and a mechanical texture (or the shape texture).
Crystallographic texture.
The crystallographic texture means a preferred orientation of the crystal lattice
of
monocrystals (grains) that form a polycrystalline material. The rocks represent single-phase
or
multiphase polycrystalline aggregates, whose preferred grain orientation is formed
during
crystallization, plastic deformation, recrystallization, creep,
b-a transitions,
sedimentation etc.
[Skrotzki, 1994].
Crystallization. The grains growing in the material during crystallization
of the substance
in the melt or in the solution acquire a preferred orientation. Type of the texture,
which is
formed during crystallization is governed by the geometric and crystallographic selection
laws.
The crystallographic selection brings the polycrystal to a state with a minimal internal
energy as
a result of a preferred growth in a direction of the crystallographic axes with the
most dense
packing of atoms. When the geometric selection is employed, origination of the texture
formation is controlled by a preferred orientation of nuclei in the substratum and
a
crystallographic direction with the maximum growth rate.
Deformation. In case of a plastic deformation of the polycrystalline materials,
preferred
orientation of crystallites
[Skrotzki, 1994;
Wenk, 1985]
takes place due to an intercrystalline
dislocation gliding
[Honicomb, 1972;
Sachs, 1928;
Taylor, 1938].
Thus, for example, while the
deformation is going on with only one slip system taking part, a single monocrystal
reorients into
position when glide plane is perpendicular to the direction of the maximum compression
and the
glide is parallel to the direction of extension. If a polycrystal having a chaotic
orientation of
grains is deformed by gliding inside each grain so that no breaks occur at the boundaries,
then
the change of shape of any grain must agree with the change of shape of the neighbouring
grains
and with the shape of the entire body as a whole. If the grain possesses five independent
slip
systems, this grain may suffer a general modification of the shape during the glide.
All grains
must follow this condition (Mises condition) so that the polycrystal would be capable
of
withstanding great plastic variations of the shape. When deformation of the polycrystal
is taking
place by way of gliding the individual grains become constrained by their neighbours
and
various rotations of the crystalline lattices are taking place in these grains. A
relative role of
rotation of the lattice may be assessed, if to assume that each grain of the polycrystal
undergoes a
similar low deformation so that deformation of the whole body is uniform. The rotational
component of the plastic deformation of each grain dictates physically appearance
of a portion
of grains (greater or smaller portion) of the volume of the polycrystal having close
orientations.
Recrystallization. Recrystallization as a physical process causing modifications
of the
structure and texture of rocks at different evolution stages can be assigned to a
various
metamorphic reactions. Formation and modification of the recrystallization textures
takes place
when the deformed geomaterial is heated or cooled down (or during deformation) and
caused by
replacement of the initial grains with a distorted lattice by new ones having a more
developed
structure. It should be noted that the mineral composition may change sometimes,
while structure
must remain unchanged or, vice versa, with the unchanged mineral composition the
size, shape
and orientation of crystallites change. Primary, cumulative, secondary and dynamic
recrystallization are recognized
[Kocks et al., 1998;
Wasserman and Greven, 1969;
Wenk, 1985].
A combination of acting recrystallization mechanisms depends upon a great number
of
parameters, including pressure, temperature, strain rate, deformation path, grain
size and a fluid
content. A properly established recrystallization mechanism based on the investigation
of the
structure and texture of the deformed rock is an essential part of the deformation
history
[White, 1977].
Shape texture.
The shape texture is interpreted as the oriented component parts with an anisotropic
outer
shape. Mechanical textures in metals, for example, are formed by crystallites having
an
extended or a fibrous shape
[Nikitin, 2000;
Wasserman and Greven, 1969].
The shape texture the rocks is created by parallel layers, streakiness of the mineral
associations,
oriented cracking and microcracking, grains of extended shape, flat and acicular
defects, oriented
intergranular boundaries
[Kocks et al., 1998;
Tectonophysics..., 1971;
Volarovich, 1972].
The value of the rock anisotropy properties depends on concentration and
configuration of pores. With all variety of the rocks the main are two types of pores
[Volarovich et al., 1974]:
- volumetric pores - their sizes are the same in all directions;
- slit-like pores (as well as microcracks) - size in one direction is several orders
greater
than in other directions.
The experimental observations have shown existence of the ordered systems of
spheroidal and needle-shaped microcracks in the rock samples
[Hadley, 1976;
Kranz, 1983].
Formation of the oriented crack hierarchies in the rocks at different scale levels
has been
studied in detail and it has general patterns that are accounted for by the existent
theories of
crack formation. The crack systems observed in nature are complicated and varied.
When the
samples are tested for compression either tensile cracks (surfaces are parallel to
the compression
axis) or shear cracks at an angle to the compression axis appear. In the first case
behavior of the
rock corresponds more to a simple compression, while in the second case it corresponds
to a
triaxial compression at a low hydrostatic pressure.
The Griffith theory
[Griffith, 1924]
is one of the early crack formation theories. Today the
mechanics and physics of rock fracture has quite a powerful instrument which was
developed by
A. N. Stavrogin
[Stavrogin, 1969],
L. M. Kachanov
[Kachanov, 1961],
S. N. Zhurkov
[Zhurkov, 1968],
E. I. Shemyakin
[Shemyakin, 1999],
G. I. Barenblatt
[Barenblatt et al., 1966],
G. P. Cherepanov
[Cherepanov, 1967],
J. R. Rais [1982]
and by others. Any material in reality has cracks
which vary in size, form and orientation. It means that tensile stresses are developed
at the ends
of some cracks even at a simple compression. The growth of favorably oriented cracks
and their
preferred orientation are due to such (induced) tensile stresses. There is evidence
that at a simple
compression cracks grow along the curved surfaces until they become parallel to the
compression axis.
Different pattern of preffered orientation in the continental crust confirm that
one of the
most important types of mechanical behavior, which appeared in the rock, in the folded
zones
connected especially, is a flow in a solid state. Some of these textures observed
in nature are
similar to textures obtained during experiment. The rocks are to capable to the conneced
flow,
evidently, at any combination of physical conditions which occur in lithosphere.
A more sophisticated models, which describe shape textures were appeared along with
development of a theory of elasticity of microheterogenous anisotropic media, based
on a
random field theory. The author
[Salganik, 1973]
has analyzed a problem related to
determination of effective characteristics of a body with the shape texture, which
considers
influence of a stress strain upon development of cracks. This was done theoretically
in the
frames of mechanics of a heterogenous continuum. More attention was concentrated
in another
work for statement and general analysis of the kinetic equation for the distribution
function of
variables, that specify form, location and orientation of the cracks in the configurational
space
[Petrov et al., 1970].
The problem related to connection of a random distributed cracks with
effective parameters of the elastic medium was analyzed in the work mentioned here
[Chekin, 1970].
Having used the approach of Eshelby as the basis for solving the problem of a solitary
ellipsoid inclusion in an infinite matrix and a generalized singular approximation
(GSA), authors
[Kalinin and Bayuk, 1994]
made a proposal to solve the problem of determination an
elastic anisotropy of the medium with the oriented penetrated cracks of an arbitrary
form and
concentration. An isotropic matrix penetrated by a system of the oriented cracks
as hollow
ellipsoids, was the model of the medium.
However, a model of origination of the shape texture in the quartz-bearing rock was
proposed even earlier
[Nikitin and Arkhipov, 1992].
First of all, influence of a thermally initiated
polymorphic transformation on the process of transition of the medium from the isotropic
state
into the anisotropic one was considered in this model; secondly, a coexistence of
three
components of quartz with different anomalous properties in the material was admitted
in the
model. It was shown that a microstructure ellipsoidal elements oriented in parallel
to large axes,
thus transferring the rock into an anisotropic state, appear in the micro-plasticity
zones, formed
due to a
b-a transition
under of non-equiaxial mechanical stresses. A tensor of the rock elastic
characteristics was also calculated.
There is a clear concept in geophysics now that the crystallographic texture and
shape
texture are central factors that control anisotropy of rocks
[Aleksandrov and Prodaivoda, 2000;
Bayuk et al., 1982;
Babuska and Cara, 1991;
Karato, 1987;
Kocks et al., 1998].
The less symmetry of crystals forming the rock is and the more contrast their own
anisotropy is the greater becomes influence of the crystallographic texture on anisotropy
of the
physical properties. The elastic properties of materials (elastic constants first
of all) and magnetic
properties of ferromagnetics are mainly controlled by the texture. The textures of
materials,
which are formed by crystallites having a non-cubic lattice, cause the anisotropy
of heat
conductivity, thermal expansion, electric conductivity and other characteristics.
1.2. Investigation of Rocks by Optical Methods, Electron
and X-ray Diffractions
Optic method for measuring the preferred orientation of grains in the rock.
As early as at the beginning of the twentieth century the optic methods for
investigation of the preferred orientation of minerals in the rock were started to
use. These are widely employed even now in the field laboratories, in the
geological expeditions and in the universities to determine the crystallographic
texture of rock samples and give some other supplementary information on the
sample mineralogy.
The fact that the useful information is limited to data about orientation of the
optic axes of
the grains arranged on the thin section only is the major disadvantage of the optic
methods. The
maximum shine method, the universal stage method and the photometric method are the
main
optic methods used for determination of preferred orientation.
Maximum shine method. The maximum shine method is based on a different speed
of
etching of various crystallographic planes. Orientation of individual grains of the
polycrystalline
rock is judged by way of analyzing angles of reflection of the light beam by the
known faces
revealed by etching [
hkl ] or the form and arrangement of the etching pits with the help of an
electron microscope or an optic goniometer.
Photometric method. The photometric method is based on interference of the
polarized
light beams passing through a crystal. The interference colors of a crystal change
if it is rotated
with respect relative to a polarizer and analyzer of the polarized microscope.
The intensity profile depending on orientation of the thin section is calculated
for a set of
grains, which is then compared with a profile obtained by a photometer. These profiles
are
decomposed into a certain number of profiles, each of them corresponding to a c-axis
orientation. These orientations may be represented on the pole figures. This method
which was
proposed by G. P. Price [1973],
belongs to integrated methods as it does not present a relation
of the c-axis orientation with orientation of single grain.
The computer-integrated polarization microscopy combines the Price method with image
processing
[Heilbronner and Pauli, 1993].
When viewing the thin section through crossed
plarizers and inserted gypsum lambda plate, it is possible to observe the change
of interference
color (orientation image). Different grains have different color depending on properties
of a
double refraction of the mineral, orientation of the c-axis and on thickness of the
section. For
example, on the thin section 20-30
m m thick in thick quartz grains taking into account
its rather
weak double refraction will display different shades of blue, yellow and the 1st
order red.
If polarizers are N-S and W-E oriented, then the quartz grain with the c-axis parallel
to the
north-south direction (azimuth
j = 0o, inclination
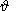 = 0o) displays red color of the
1st order.
During clockwise rotation the interference colors change:
j = 45o - blue,
j = 90o - red,
j = 135o - yellow,
j = 180o - red. During the complete
revolution this sequence repeated twice. The
increase of inclination angle and shifts of the c-axis reduce the color contrast
the blue and yellow
towards the red color of the 1st order up to an extreme case, when the c-axis becomes
perpendicular to a plane of the thin part of the section (at
= 0o) displays red color of the
1st order.
During clockwise rotation the interference colors change:
j = 45o - blue,
j = 90o - red,
j = 135o - yellow,
j = 180o - red. During the complete
revolution this sequence repeated twice. The
increase of inclination angle and shifts of the c-axis reduce the color contrast
the blue and yellow
towards the red color of the 1st order up to an extreme case, when the c-axis becomes
perpendicular to a plane of the thin part of the section (at
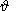 = 90o the grain shows the red
color
irrespective of angle
j ).
= 90o the grain shows the red
color
irrespective of angle
j ).
If the c-axis of the quartz grain is aligned on all the possible directions, then
having
recorded the observed interference colors on an equal area projection, we obtain
an interference
color stereogram (ICS). Let us note that this stereogram can be obtained by calculation
from the
interference spectrum for each position of ( j, 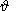 )
on a stereographic net. The ICS can be
considered as the color maps, which correlate the specific colors with orientation
of the c-axes.
)
on a stereographic net. The ICS can be
considered as the color maps, which correlate the specific colors with orientation
of the c-axes.
Due to a symmetry of the quartz crystal, however, relation between color an orientation
is
not unambiguous. Usually in practice the microscope stage is rotated to obtain supplementary
information about orientation of the grain. A sequence of colors should be established
for any
given initial position. Further, the rotation required for coincidence with the red
color of the 1st
order, fixes the azimuth
j, and the color contrast intensity between the
yellow and blue zones
determines the angle of inclination
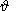 . The problem of definition the signs is resolved
by
inclining the section relative to the microscope stage. Thus, orientation of the
c-axis is defined
unambiguously.
. The problem of definition the signs is resolved
by
inclining the section relative to the microscope stage. Thus, orientation of the
c-axis is defined
unambiguously.
Universal stage method. The described above methods of investigation of the
optical
properties of crystals are developed applicable to the polarizing microscope with
a stage rotating
around one axis i.e. the microscope axis.
E. S. Fedorov developed a new method in principle at the end of the XIX
century and he
named it as U-stage or theodolite method
[Fedorov, 1893].
Analysis of crystals by this method is
done on a special (Fedorov) stage, which is fixed on a conventional stage of the
polarizing
microscope. The Fedorov stage has several axes allowing to take the object under
investigation
from a position perpendicular to the microscope azis and to rotate it in different
space directions.
Measurement of the rock grains orientations on the U-stage is based on the anisotropic
optic properties of crystals. The properties depend on crystal symmetry and may be
described
by the optic indicatrix with its principal axes
na, nb,
ng.
In the case crystals of trigonal, tetragonal and hexagonal crystal symmetry one optical
axis exists and coincides with the main symmetry axes of crystal. In the uniaxial
minerals
(quartz, calcite) the c-axis is the single "optical'' direction which can be measured.
Two or more
crystallographic directions must be determined in addition to the c-axis to obtain
a complete
orientation. The optical method is not helpful for the purpose in the case of quartz.
Triclinic, monoclinic and orthorhombic minerals posses two optic axes. Orientation
of the
optic indicatrix relative to the crystallographic axes is more complicated than in
the uniaxial
case. It depends on the symmetry of the crystal and on a chemical composition of
the mineral. In
orthorhombic minerals (olivine, for example), the optic indicatrix axes are parallel
to the main
crystallographic directions, and, hence, a complete orientation can be determined
directly from
the measurements of indicatrix.
In monoclinic minerals (hornblende) the indicatrix axis deviates from the crystallographic
c-axis by different angles depending upon the composition of the mineral under investigation.
Therefore, a supplementary information is required for an unambiguous definition
of the
orientation of crystal. For triclinic minerals like plagioclase, none of the main
crystallographic
directions can be defined directly from the indicatrix. Its relative positions change
in dependence
on the mineral composition
[Benn and Mainprice, 1989;
Kruhl, 1987].
Therefore, to determine a
complete orientation of the low-symmetric minerals orientation of at least one crystallographic
plane must be measured in addition to the indicatrix axes.
A procedure for determining the preferred orientation of minerals in the rock samples
was
developed by B. Sander
[Sander, 1923].
Electron diffraction.
The use of the scanning electron microscope (SEM) for determination of the preferred
orientation of grains is a rather new method and, therefore, it is not very widespread.
The
electronic channeling (EC) and the electronic backscattering diffraction (EBSD) methods
are
distinguished. Fundamentals of the SEM method are described in detail in the work
of
[Holt et al., 1974].
As a result of the electronic channeling unique configuration of lines and bands,
which
characterize orientation of the crystallite at the point of beam incidence, is obtained.
The EC technique
[Lloyd, 1994]
is based on the fact that a small portion of backscattered electrons
originated from the "channeling'' of incident electrons between the lattice planes.
To maximize
the emission signal due to a partilinear set of atomic planes, the angle of incidence
between the
electronic beam and the planes must change by at 2
Q during the scanning process. Moreover,
the beam must be collimated because changes in emission can be observed only when
a great
part of electrons move in the same direction. The EC image recorded by electron microscope
is
a point diffraction pattern, which can be considered as a practically non-distorted
projection of
a reciprocal lattice plane.
Electronic back-scattering Kikuchi patterns create a geometrically equivalent images.
EBSD form when a stationary beam strikes an inclined sample so that the incident
beam has
relatively low angles of incidence (~10-30o). An optimum spatial resolution
of the EBSD method
is 0.1-1.5
m m that is better than for the EC method (1-10
m m). However, the sample is
inclined and this causes anisotropy of resolution. The angular range of EBSD is ~40-80o,
unlike
the EC ~20-25o. The large range of EBSD helps to index the reflexes.
Analysis of the EC pattern is based on comparison of a pattern obtained on a sample
with
the so-called "ECP maps'' (electronic challenging pattern) made up of individual
EC events.
These maps contain the mineral lines pattern and can be represented on a spherical
surface or as
on to projection on to plane. In order to determine the mineral grain orientation
the sample
picture, which is a small section of the whole pattern brought into unequivocal coincidence
with
the pattern on the ECP map. The lines are indexed and orientation of the grain relative
to the
coordinate system of the sample is found with the help of necessary rotations. The
patterns can
be compared visually, but computer-aided indexing and plotting of fabric diagrams
for each
crystallographic direction is done in practice
[Schmidt and Olesen, 1989].
An orientation imaging microscopy method (OIM)
[Adams et al., 1993]
is an automated analysis of the electronic backscattering pattern for orientation
mesurements. The sample is fixed
on the microscope stage for a two-dimensional positioning. The EBS pattern is observed
on the
screen with the a high-resolution camera-recorder, fixed by computer and orientation
of the
crystal is determined automatically. While the sample is analyzed the stage is shifted
to a new
position and pattern of another grain is recorded. Thus, the sample surface is scanned
on a
regular grid with the selected step size. A practicable rate is about 3000 measurements
per hour
thus allowing to obtain statistically reliable data in a short period of time. To
date the ORM
method is restricted by monophase materials. The use of this method might be connected
with
resolving also specific problems related to local investigations such as determination
of the
recrystallization nuclei orientation etc.
X-ray method.
Measurement of the pole figures with the X-rays is based on diffraction when radiation
of
given range is scattered on the atoms of crystalline lattice. The scattering originates
from induced
oscillations of the atom electrons under the influence of the electromagnetic field
of the X-ray
incident wave. The X-ray diffraction is widely applied to crystals because the order
of the
interatomic distances in a crystal is the same as order of the X-ray wave length.
Two waves
reflected from the similar lattice planes with the distance dhkl is characterized
by a path
difference
D. If
Dnl ( l - the radiation wavelength,
n - the integer value),
then the interfering waves completely delete each other.
Intensity is observed only if
D=nl.
Connection between
l, dhkl and angle
q, between the
incident beam and the reflecting lattice can be determined from purely geometrical
relationship
(Bragg's law). By keeping
l constant and changing
q, it is possible to record a complete
X-ray
diffraction pattern, if the crystal is in a reflecting position for all lattice planes.
The X-ray experiment is done in the following way. The sample is placed in the center
of
circle of the goniometer circle. The incident beam falls on the sample at an angle
q, the reflected
beam can be seen at an angle
2q with respect to the primary beam. This condition
is fulfilled, if
the focusing circle intersects the goniometer circle at the collimator and receiving
slit position
and contacts the sample surface as well. The dispersion vector corresponds to a normal
to the
lattice plane ( hkl ), which is in a reflecting position.
During measurement of pole figures the
q is set to the correct value of the desired Bragg
reflection ( hkl ) and remains constant. The spatial orientation of the sample is
changed
systematically and the intensity
Ir of the reflected beam is measured for each position. The
reflected intensity is proportional to the scattering volume part of the volume
Vhkl, if the the size
of grains in the sample is not uniform, it is also proportional to a number of the
reflecting
crystallites
Nhkl.
Sample positioning is made with the help of the Euler cradle by rotating the sample
about
two perpendicular axes. Two X-ray experiment conditions are recognized:
1) back reflection mode (the scattered beam is observed at the same side of
the sample);
2) transmission mode (the scattered beam passes through the sample).
Advantages and disadvantages of indicatrd X-ray experimental mode are as follows.
The
texture of the polycrystalline material is a statistical ensemble of crystallites,
so to obtain a
meaningful mode a statistically representative number of crystallites or grains is
required. It is
necessary to have 104 up to 105 grains to get reproducible pole figures.
The known properties of
the X-rays, namely a strong absorption by the material and a small diameter of the
beam limits
their use for small and thin samples and for the fine-grained material with the grain
size below
10-20
m m. These limitations of the method permit to
investigate the sample surface only as the
X-rays penetrate the sample just from few to several micrometers. The X-rays measure
the local
texture on the sample surface. It is possible to get only incomplete pole figures
because of the
high orientation dependent absorption and limitations by defocusing (broadening of
peaks due to
different cross sections of the reflected beam) of the Bragg reflection, when a flat
sample is
inclined. This disadvantage might be overcome partially by a precise scanning equipment,
e.g.
a combination of measurements in transmittion and reflection geometry as well as
sophisticated
data analysis. Usually the X-ray diffraction is limited to monomineral rocks of orthorhombic
or
higher crystal symmetry.
A comparative analysis of texture measurements of the carbonate rock samples, performed
by the X-ray and the neutron diffraction methods, was made in the work by
[Wenk et al., 1984].
The authors
[Ullemeyer et al., 2000]
made a comparison of texture determination of two-phase
muscovite-quartzite sample with four different methods used in the geological sciences:
optical
U-stage, electron backscattering diffraction, X-ray back reflection texture goniometry
and time-of-flight
neutron diffraction. The work discusses advantages and disadvantages of these methods
in investigation of geological materials.
1.3. Measurement of Pole Figures by Neutron Diffraction.
Main Advantages of the Neutron Diffraction Texture Analysis
The major task of the texture analysis lies in obtaining information about the distribution
of
crystallite orientations in the sample under investigation. Preferred orientations
are visually
represented by pole figures. A graphic representation of the distribution function
Phkl of normal
poles to one specific crystallographic plane ( hkl ) is also often referred to as a pole figures. The
function
Phkl proper is called the pole figure. Stereographic projection
is usually used for
graphic representation of the function. The function
Phkl is the probability of coinciding the
normal to ( hkl ) plane with different directions in the sample.
The normal to the ( hkl ) plane in respect to the sample coordinate system is specified by
the polar angle
F and azimuth
g, where
g=(F-p).
Thus, the distribution
function
Phkl is represented as
Phkl (F, g).
Any function which depends on the direction can be
expanded in a
series in spherical functions
kml. The function
Phkl is expanded in the symmetric spherical
functions
kml with
the symmetry of the sample.
Phkl (F, g)
is presented as
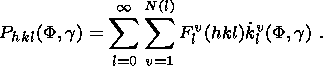 | (1) |
In practice the infinite series (1) is replaced by a finite sum, breaking at a certain
l=lmax.
The expansion coefficients are expressed in terms of the experimentally pole figure
as
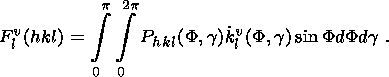 | (2) |
Measurements of pole figures are by neutron diffraction are carried out on sphere
or
more frequently on cubic samples. While texture samples with polished surfaces or
thin sections
are necessary for X-ray diffraction, no special preparation for neutron measurements
is needed.
Furthermore, neutron diffraction allows to measure complete pole figurers.
Modern texture diffractometer equipped with the position-sensitive or multidetector
system
[Schäfer, 2002]
permits to measure several pole figures simultaneously. Moreover, the
special profile analysis is applied to separation of overlapping Bragg reflections
on the spectra
[Ullemeyer et al., 2000].

|
|
Figure 1
|
The textured polycrystal sample, practically at its any position with respect to
the neutron
beam, has groups of crystallites arranged in the way that the Bragg condition is
fulfilled. In order
to determine the orientational dependence of the intensity of the given reflex ( hkl ), it is necessary
to rotate the sample with respect to the incident beam. A special texture goniometer
is used for
this purpose. An individual diffraction spectrum corresponds to each sample position.
Determiing the integral intensity of one reflex from this
spectrum we obtain a value of the pole
density for one point corresponding to angles
Q and
j on the pole figure. Because one can
calculate the pole densities at the same point for different pole figures determining
intergrated
intensities of these Bragg reflections (Figure 1).
The pole figures are indexed after the reflexes caused by
the scattering of a given wave
length from the crystallographic planes with same parameter of the lattice
d (Figure 1).
Theoretical spectra, calculated with the structure parameters of crystals by Bragg
diffraction
law, are used for indexing the spectral maxima. To find the pole density the integral
intensity of
reflexes with identical indices (each diffraction peak is approximated by a normal
distribution) is
to be determined. For calculation of the pole density background values are determined
over
reflex interval. Corrections to be reflectivity of the interplanar spacing sensitivity
of detectors
etc are introduced. As a result, figures form the data arrays the pole densities
and may be
visualized on a stereographic projection.
The main advantages of neutron scattering application for texture analysis of geological
material:
(1) high statistical representation (thousands of grains compared with hundreds
of grains,
measured by optic microscope);
(2) investigation of volume textures rather than local (surface) textures by
X-ray
diffraction;
(3) study of both coarse-grained and fine-grained natural materials;
(4) texture analysis of low-symmetry minerals;
(5) investigation of multiphase rocks, permitting a texture analysis of individual
mineral
components, that is not possible for other diffraction methods and for direct methods
of the
texture analysis;
(6) investigation of the texture evolution of samples placed in chambers at
the high
pressure and temperature, that is not possible both for other diffraction methods
and for direct
methods of the texture analysis.
The quantitative texture analysis using neutrons is applied now to monomineral and
multiphase geological materials
[Chateigner et al., 1999;
Lobanov et al., 2002].
The application of a new Riveld technique combined to ODF calculation will be method
of choice in
polycrystalline diffraction-data evaluation. The main targets are to obtain the orientation
distribution in the case of low-symmetry compounds and to analysis the crystal structure
in the
presence of strong texture.
Several attempts were made to combine structure, texture and stress/strain analysis
using
neutron diffraction. R.-H. Wenk
[Wenk et al., 1994]
proposed a method using the whole
diffraction spectrum rather than extracted peak intensities by combining the quantitative
texture
analysis with the Rietweld crystallographic method. The feasibility of the Ritweld
texture
analysis are demonstrated with neutron time-of-flight data of experimentally deformed
calcite
[Lutterotti et al., 1997].
It was possible to obtain a quantitative information on texture, crystal
structure, microstructure and residual stresses on the basis of incomplete pole figures
and from
regions of the diffraction spectrum containing the overlapping peaks. Neutron diffraction
has the
potential to investigate evolution of microstructures, including the dehydration,
phase transition,
structural changes in the minerals as well as stresses/strain using experimental
and measuring
complexes such as SKAT-CUC and EPSILON-MSD (Dubna, Russia) or HIPPO (Los Alamos,
USA).
1.4. Quantitative Texture Analysis
Mathematically the crystallographic texture is described in terms of the orienrarion
distribution function (ODF)
[Bunge, 1982;
Matthies, 1979;
Matthies et al., 1988;
Viglin, 1960].
However, ODF cannot be obtained directly from the experiment. It is possible to measure
only
its integral projections, pole figures (PF), which represent intensities of the diffraction
reflections
from certain crystallographic planes of crystallites. The main task of the quantitative
texture
analysis is the ODF computation from a finite number of experimental number of PFs.
Methods
of Roe-Bunge
[Bunge, 1965;
Roe, 1965]
and the ODF approximations by standard functions
[Bukharova and Savelova, 1993;
Nikolaev et al., 1992;
Savelova, 1984;
Savelova and Bukharova, 1996]
are most widely employed to resolve this task.
The relative orientation of crystallographic axes of crystallites in the polycrystalline
material can be determined by rotation of
g. If to assume that the orthogonal coordinate system
KA (laboratory coordinate system) is connected with the
sample under investigation and the
orthogonal coordinate system
KiB (crystallite coordinate system) is
connected with the
crystalline lattice of the
i -th crystallite, then orientation of
g defines the rotation that transforms
the coordinate system
KA into
KiB. This rotation is set by three Euler
angles
{j, 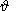 , y} and belongs to a rotation group of a three-dimensional
Euclidean space
SO (3).
, y} and belongs to a rotation group of a three-dimensional
Euclidean space
SO (3).
The ODF
f(g) defines a volumetric part of crystallites of the material whose
crystallographic coordinate system is turned with regard to the laboratory system
through angles
j ,
,
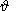
 and
y
and
y ,
lying inside a solid angle
dg,
which represents an invariant measure on group
SO (3):
,
lying inside a solid angle
dg,
which represents an invariant measure on group
SO (3):
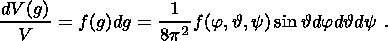 | (3) |
The integral of this function on a certain domain
u is interpreted as a probability to find a
random orientation
g in this domain.
If a certain crystallographic plane with the normal is selected in the system then
the PF
Phi( y) determines a volumetric
part of crystallites, for which different directions
y of the coordinate system
KA are in the infinitesimal volume with the normal
hi directions to the
i -th crystallographic plane of crystallite. Let us note that directions
y and
- y, as well as
directions
hi and
- hi, are indistinguishable physically in the experiment
and, consequently, the
relevant PF become indistinguishable. Then probability that volume
v of the randomly oriented
crystallites in the sample will have a direction
hi is
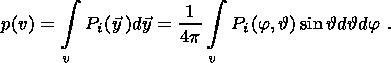 | (4) |
Here,
j and
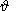 - spherical coordinates of the vector
y. The ODF
f(g) and PF
Pi( y) are bound together by an integral relation:
- spherical coordinates of the vector
y. The ODF
f(g) and PF
Pi( y) are bound together by an integral relation:
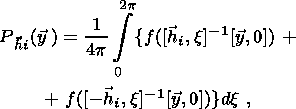 | (5) |
where
[ y, 0]={j, 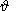 ,
0} - rotation in
SO (3),
[ hi, x]-1
- rotation reverse to
[ hi, x].
,
0} - rotation in
SO (3),
[ hi, x]-1
- rotation reverse to
[ hi, x].
Thus, solution of the task of restoration of ODF from PF mathematically is in finding
f(g), satisfying the system of the integral equations (3), from the
finite set obtained from the PF
experiment
Phi( y).
A method for calculation of ODF proposed in the work of
[Bunge, 1965;
Roe, 1965]
has received a wide recognition. This method consists in presentation of ODF as a
series of
generalized spherical harmonics and the pole figures as a series of spherical harmonics.
In this
case for ODF
f(g), the following expansion in series of generalized spherical harmonics
Tlmn(g) is right:
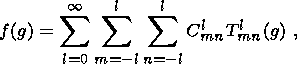 | (6) |
where coefficients of the ODF expansion in series are found in the following way
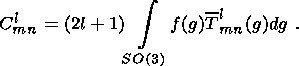 | (7) |
Here and further the complex-conjugate functions are marked with a bar.
The PF can be presented as an expansion in series of spherical harmonics
Yml( y):
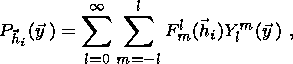 | (8) |
where
Flm( hi) - expansion
coefficients. The integral relation (5) and expansion in series (6)
give the following formula, which expresses the PF through the ODF expansion coefficients
Clmn:
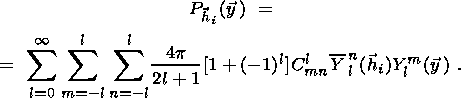 | (9) |
Relations (8) and (9) in the Roe-Bunge method are considered systems of the algebraic
equations for the unknown
Clmn, which are usually found by the least-squares
method. A priori
information about symmetry of the crystallite and the sample (number of unknowns
reduces)
and about sharpness of the texture (preliminary information about the expansion length
(6) of
truncated series) is used for an unambiguous determination of these coefficients.
Let us note, that it follows from the relation (9) that the pole figures do not depend
on
the odd component of ODF. Therefore, knowledge even all theoretically possible PF
can present
information only about the expansion coefficients of the even component of the ODF.
Thus, the
ODF cannot be determined unambiguously, in principle, from PFs
[Matthies, 1979].
A number of methods has been developed recently, which with some additional
assumptions about the ODF, permit to find a unique solution to the ODF reconstruction
problem
from PFs by introducing a priori constrains about the ODF structure. The ODF approximation
by normal distribution on group belongs to these methods. In this case, the ODF might
be
presented as a linear combination of normal distribution on group
SO (3)
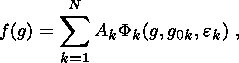 | (10) |
where
Ak - positive coefficients (weight),
Fk (g, g0k,
ek) - normal distribution with
maxima at the
point
g0k, ek
- scattering parameters (analogs of dispersion). These parameters are found using
the comparison of the theoretical PFs from ODF of form (8) with the experimental
PFs, for
example, with the help the least-squares method.
One of the first proposed approximations of ODF with a normal distribution is in
the
work of
[Bunge, 1982].
This distribution was obtained by analogy with the known Gaussian
distribution on a straight line.
However, ODF construction on the basis of a central limit theorem of the probability
theory of is a more rigorous approach. This approach exactly was employed in the
work by
[Savelova, 1984;
Savelova and Bukharova, 1996],
where circular and non-circular normal
distribution, so-called central normal distribution, is analyzed. The central normal
distribution is
given by:
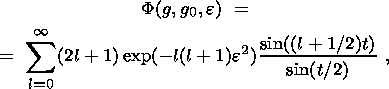 | (11) |
where
cos t=(Tr (g-10 g)-1)/2.
The PF responding to this distribution are written as
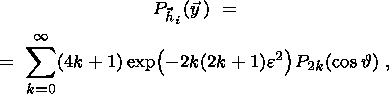 | (12) |
where
P2k ( cos  )
- normalized Legendre
polynomials, and
cos
)
- normalized Legendre
polynomials, and
cos =( hi
=( hi g0 y).
Functions (11) and (12) can be approximated by more simple
expressions:
g0 y).
Functions (11) and (12) can be approximated by more simple
expressions:
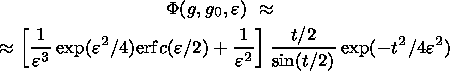 | (13) |
for ODF and
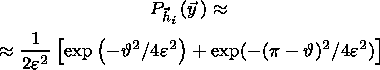 | (14) |
for PF. Representations (11) and (12) were used in the work by
[Bukharova and Savelova, 1993;
Helming, 1993;
Nikolaev et al., 1992]
for polycrystalline materials of different symmetry.
A component method
[Helming and Eschner, 1990],
which is applicable to crystals of any
symmetry is rather frequently used for a quantitative texture analysis. It is important
to note, that
this method permits to make the texture analysis of two and more mineral phases
simultaneously.
1.5. Neutron Spectrometers for Investigation of Textures,
Stresses and Properties of
Geological Materials in the World Research Centers
The neutron texture diffractometers are capable of functioning
in the same way as the X-ray
diffractometers on a constant wave length on stationary reactors or they may use
a time-of-flight
method on the pulse reactors and accelerators. The main parameters of the experimental
assemblies used in different research centers for investigation of textures of the
polycrystalline
and the geological materials are presented in Table 1.
Diffractometers on steady-state neutron sources.
The simplest diffractometer situated at a thermal beam tube of a steady-state reactor
matches a conventional four-cirdle diffractometer equipped with the Euler cradle
as a
goniometer and single-county tube, i.e. it is an instrument for investigation of
structure of
monocrystals. Measurements of sample-orientation-dependent intensities are made with
the of a
detector, positioned stationary position in the peak maximum, i.e. a step scanning
is performed
on an equal-area grid of the pole figure. The TEX-2 at the research reactor FRG-1
in GKSS,
which is dedicated to texture analysis (predominantly of high-symmetry materials)
[Brokmeier et al., 1998]
belong to this type of diffractometer. In the case of the instrument with single
detector, pole figures, needed for restoration of the ODF, are measured one after
another, which
is a time-consuming procedure.
Instruments equipped with a system of the
position-sensitive detectors are very effective for the
texture analysis of the geological materials. The biaxial
spectrometer D1B and the powder diffractometer D20, which are
functioning in the Laue-Langevin Institute (Grenoble, France), are
suitable for texture measurements.
The D1B spectrometer at the high-flux source ILL in Grenoble
[Wenk et al., 1986]
was the first instrument for the texture
investigation of the low-symmetric plagioclase. The D1B
spectrometer has a system of replaceable monochromators and a
movable multidetector module. The spectrometer is outfitted with a
special cryostat to perform experiments over a wide temperature
range.
The diffractometer D20 is characterized by a linearly bent position-sensitive detector
system as well as a wide operation wavelength-range.
The texture diffractometer SV7-b mounted on the neutron beam in the experimental
hall of
the research reactor FRJ-2 operates in the Jülich
(Germany) Research Center.
The instrument is equipped with various monochromators crystalline coatings that
make
possible obtaining the wave length ranging from 0.9 up to 2.3 Å. The use of special ( l /2)-filters,
which suppress the higher order noise, permits to improve the experimental pole figures
that are
recorded during investigation of the geological materials.
The texture diffractometer is supplied with position-sensitive scintillation detector
of the
JULIOS-type mounted on the free-rotating platform. It is capable of covering an angle
of
D2Q=50o.
The detector has also the replacement Euler cradles that permit making measurements
on the
sample, both under normal conditions and under low temperatures, by placing the cradle
inside
a helium cryostat.
Owing to the position-sensitive detector the SV7b diffractometer is used as a working
instrument for investigation of rocks mainly
[Ghildiyal et al., 1999;
Jansen et al., 1992;
Will et al., 1990].
Diffractometers at pulse neutron sources.
The fact that the thermal neutron reactor impulse has a continuous spectrum, the
thermal
neutron velocity is low and there is a possibility of making the neutron energy analysis
(or the
wave length) in the time of flight (or TOF experiment) may be considered as the feature
dictating the procedure and scheme of the diffraction experiment on the pulsed sources.
The texture diffractometer - SKAT
[Ullemeyer et al., 1998]
functions on the IBR-2 pulsed reactor (JINR, Dubna, Russia). Its detector system,
containing nineteen
detectors, is arranged on a mounting ring 2 m in diameter, which is axially
symmetrical with respect to the neutron beam.
The resulting time-of-flight path (distance between the moderator and detector) is
103.8 m. The
detectors can be fixed at any position of the angular interval
2p, covered by the detector ring.
The scattering angle is the same for all detectors ( 2q=90o ). The sample to
be investigated is
placed in the center of the ring and is rotated in the goniometer, which accepts
of the apparatus
up to 30 kg mass, around the horizontal
Z axis arranged at angle of
45o to the incident neutron beam.
The SKAT spectrometer has advantages as compared with other similar instruments:
- Diffraction peaks corresponding to a specific
dhkl value, are recorded by all detectors in the
same position (time-of-flight channels) in all diffraction spectra obtained from
the
measured sample. Therefore, there is no need to introduce corrections which depend
on the
scattering angle and the wave length;
- since the angular range of the detector set up is
180o, it is sufficient a single sample
revolution on a goniometer to measure the complete the pole figure;
- important is that various systems such as heaters, high-pressure chambers,
devices
creating electrical and magnetic fields, etc. can be placed around the sample in
the center at
the SKAT detector ring.
The main advantage of TOF diffractometers and SKAT included is in a possibility to
record different pole figures in simultaneously in a reasonable time. This is especially
important
for making the texture measurements of the low-symmetry and multiphase geological
materials
[Feldmann et al., 1991;
Ivankina et al., 1999b].
A high-resolution neutron spectrometer NSHR
[Walther et al., 1993b]
which was used for the texture measurements starting from 1998 is arranged on the
same beam at the IBR-2
pulsed reactor in Dubna. Presently a upgrading is going on the NSHR diffractometer
as it is
necessary to extend the texture measurements of the geological samples.
The ROTAX instrument installed at the ISIS pulsed spallation source in the Rutherford-
Appleton laboratory (Great Britain) has been operated for several years as a multipurpose
powder and texture diffractometer outfitted with position-sensitive JULIOS detectors.
Functioning as an angle-dispersive TOF diffractometer with the time-of-flight path
of about 15
m permits to use the polychromatic neutron spectrum effectively. It should be noted
that,
combination of a white beam TOF method and the use of the linear detector pursue
two goals
simultaneously: 1) to reduce the number of rotations of the sample during scanning
of the pole
figure, 2) to measure simultaneously a great number of the pole figures with
different ( hkl ).
The texture analysis using TOF method and two-dimensional detector system was made
at the LANSCE pulse neutron source in Los Alamos (USA) and IPNS of the Argonne National
laboratory (USA). Various pole figures are scanned due to different positions of
the sample on
diffractometers, which were originally designed for diffraction on monocrystals and
supplemented with a goniometer and two-dimensional detectors.
A HPPO (High Pressure - Preferred Orientation) diffractometer for measurement of
the
preferred orientation at high pressure was actually put into operation in Los Alamos
[Bennett et al., 1999].
The high-intensity TOF diffractometer has a short time-of-flight path (9 m)
and it will
be used mainly for investigations at high pressure and for the texture measurements.
It exhibits a
new three-dimensional arrangement of the detector banks with 1400 helium tubes located
on five
conic rings corresponding to a position at angles of
2Q = 10o, 20o,
40o,
90o and 150o. The measured
interplanar spacing ranges from 0.5 to 9.0 Å.
A conventional three-axial goniometer using with
the Kappa geometry was used for standard texture measurements. A device for changing
position
of the sample (32 positions) permits to make the texture analysis of a multiphase
sample in a
fast way and this is important for systematic investigations of large groups of the
geological
samples.
The systems surrounding the sample are made specially to study the samples at a wide
range of temperature (4K
Along with the study of the texture changes in materials at different thermodynamic
parameters, structures of the substance, internal stresses, magnetic properties of
different
materials etc. are also studied on the diffractometer. Spallation in a wide pressure
and
temperature range will make it possible to conduct
in situ dynamic measurements of chemical
reactions, deformations and recrystallization processes.
The study and determination of the crystallographic textures in the research center
of the
Argonne National laboratory (USA) is done with the help of the general purpose powder
diffractometer (GPPD) at the intensive pulse neutron source (IPNS). Design of the
instrument
and different component facilities allow to solve a rather wide spectrum of material
science
problems. A moving multidetector system of the diffractometer assists to study with
a rather high
accuracy the structural parameters, microstresses and textures of materials. There
is also
possible to carry out experiments with heaters and high-pressure chambers. An extensive
biological shielding and the relatively remote location of the instrument allows
to work even
with highly radioactive samples.
Till today, information regarding possibilities of neutron diffraction in the texture
analysis
of rocks is not so widespread among geologists and geophysicists. The reason is in
a limited
number of neutron diffractometers and in a restricted time for measurement, especially
if a large
collection of samples is to be analyzed. Further efforts are necessary to propagate
technology
acquired by crystallographers and materials technologists over many years in the
field of the
quantitative texture and strain/stress analysis and its application in geosciences.
II. Textures and Physical Properties of Rocks and Meteorites
2.1. Textures and Elastic Properties of Rocks at High Hydrostatic
Pressures
As has been already mentioned in chapter 1.1., anisotropy of the rocks is dictated
by the
conditions, which were established at different depths, and by structure of the rocks,
for
example, by the crystallographic texture. Formation of the crystallographic texture,
in its turn, is
connected with certain physical processes in the lithosphere, such as plastic deformation,
creep,
recrystallization etc.
Ivankina et al., [1999a]
have started a complex investigation of factors, which
influence the elastic anisotropy of the mantle rocks at different hydrostatic pressures.
The
neutron diffraction texture analysis by the NSHR diffractometer and ultrasonic measurement
of
the longitudinal wave velocities on spherical samples were employed for the purpose.
Later
these studies were continued with the SKAT
[Nikitin et al., 2001a].
Some results obtained with the SKAT diffractometer for some samples of xenoliths
and
dunites taken from different regions of Europe. The samples tested were mainly single-phase
rocks formed by forsterite (olivine). Specific data about composition, samples locations
and
origin of the samples are in the paper
[Nikitin et al., 2001a].

|
|
Figure 2
|
A quantitative texture analysis of the samples was made on
the basis of neutron-diffraction
measurements of the xenoliths and dunites samples and of a set of experimental pole
figures.
Using ODF the pole figures for the main crystallographic planes (100), (010) and
(001) were
calculated (Figure 2),
which describe the preffered orientations connected with the extreme
directions of the elastic wave velocities in the olivine crystal.
The preffered orientations of planes (100) in samples 9721, 9722 (Ivrea zone, Italy),
BQ4
(Albania) and NA5N (Norway) are represented as belts with well expressed maxima distributed
along the belts. A rather compact maximum with a high pole density is observed on
the (010)
pole figure. The pole figures (001) are characterized by a complicated configuration
of isolines
with several overlapping maxima.
Quite different pattern is observed in the xenolith samples OLIV1 and OLIV2 (Canary
Islands). High intensity compact maxima on the (100) pole figures are typical for
texture of these
samples, while orientation of the (010) and (001) base planes originates or has a
tendency to
originate of belts with a pronounced pole density maximum.
Texture of olivine in xenoliths SEM1 and ZB1 ( Z elezny Brod, Czech Republic) is less
sharp then in xenolithes from the Canary Islands, thus affecting values of the maximum
pole
density on the pole figures and it is more fuzzy, though pole figures of samples
display thr
similar configuration of isolines.
The quantitative information about texture in terms of ODF, restored from the diffraction
data, allowed to simulate of the elastic wave velocity in the polycrystalline olivine
samples
having a crystallographic texture
[Nikitin et al., 2001a].
This simulation implied the calculation of
elastic stiffness tensor of polycrystalline sample by the known averaging methods
based on the
ODF and elastic modules of the olivine monocrystal as well as construction of the
stereoplots
reflecting spatial distribution of velocities on P-wave in the sphere. Tabulated
values of
components of the olivine elastic constant tensor are taken from
[Simmons and Wang, 1971].

|
|
Figure 3
|
The computed maps of isolines of the spatial distribution
of the P-wave velocities in the
coordinate system corresponding to the position of the sample in the diffraction
experiment are
shown on Figure 3.
Velocities of the longitudinal elastic waves at different confining pressures were
measure
for the same samples by the ultrasonic method
[Pros, 1977].
The method is, that emissin and
reception of the ultrasonic pulses is effected by two piezoacoustic transducers having
a point
contact with the same surface, in different directions along the diameter of the
spherical sample.
The electroacoustic transducers move in the plane passing through the axis of rotation.
The
proposed system permits to measure the elastic impulse travel time in any direction
and to
calculate velocities. When the sample rotates discretely at a step of
15o one obtain a set of 150
points, which are marked stereographic grid related to the coordinate system of the
spherical
sample. It should be noted, that orientation maps of the elastic P-wave velocity
and pole figures
from the diffraction experiment are constructed in the same coordinate system.
Velocities of the longitudinal elastic wave were measured in a cyclic way: first,
at the
atmospheric pressure; then at the pressures of 10, 20, 50, 100, 200, 400 MPa
and in the reverse
order with exactly the same values on the load scale
[Ivankina et al., 1999b;
Locajicek et al., 1999;
Nikitin et al., 2001a].
Maximum and minimum velocities of the longitudinal waves as
well as anisotropy factors,
which were calculated by the following formula, are given in Table 2
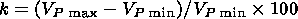 | (15) |

|
|
Figure 4
|
It is seen from Table 2 that the investigated samples at the atmospheric pressure
are
characterized by a high anisotropy of the P-wave velocities. The anisotropy factor
of samples
9721 and 9722 practically does not change along with increasing pressure. Such behavior
of
samples is confirmed by the dependence of the anisotropy factors of the P-wave velocities
k upon hydrostatic pressure (Figure 4). The elastic anisotropy of various samples
differs significantly
with the hydrostatic pressure rise. Dunite samples 9721, 9722 and BQ4 form one group
whose
anisotropy factors do not change practically with the pressure increasing, and xenolith
samples
SEM1 and ZB1 demonstrate decrease of the anisotropy
k at pressures up to 100 MPa followed
by its monotonous increasing.

|
|
Figure 5
|
Figure 5 shows maps of the P-wave velocity isolines, constructed
from experimental
data, obtained at 0.1, 100 and 400 MPa for the same samples which reflect a spatial
variations
of the elastic anisotropy with pressure increasing. Dunite samples 9721 and 9722
have stable
patterns of the P-wave velocity distribution throughout the hydrostatic pressure
range. For
sample BQ4 configuration isolines changes with the increasing of pressure, directions
of the
velocity maximum and minimum (to a greater extent) on the stereographic projection
are
shifted, but the pattern basically stabilizes. The counter maps of the samples ZB1
and SEM1
(Figure 5)
show no regular distribution at atmospheric pressure. With the pressure rise the
isolines
acquire a more perfect and symmetric configuration. Positions of the velocity maxima
and
minima are shifted and in case of sample ZB1 they are switched. With a further pressure
rise
from 100 up to 400 MPa the spatial distribution of velocities become more smooth.
The model distributions
Vp (Figure 3) obtained from the ultrasonic experiment
at 400 MPa
(Figure 5).
This fact provides evidence that elastic anisotropy of these rocks at high pressure
is
mainly controlled by the crystallographic olivine texture. Nevertheless, some difference
in the
model and experimental patterns concern the maximum and minimum velocities and elastic
anisotropy
k. Only one factor having influence on the elastic anisotropy of the bulk
sample of
dunite or xenolith - crystallographic texture was taken into consideration in simulation
of the P-wave
velocity distribution. Evidently, influence of the form texture (presence of the
oriented
cracks, intergranular boundaries etc.) or vice versa, presence of the random oriented
defects even
at a high uniform pressure might cause of anisotropy increasing, induced mainly by
the
crystallographic texture, as well as its decreasing.
2.2. Textures and Piezoelectric Properties of Rocks

|
|
Figure 6
|
The volumetric piezoelectric effect in rock occur if, in addition
to preferred orientations
of the electric axes of crystals, these axes have orientational polarity (Figure 6).
The first statement about existence of piezoelectric properties of rocks appeared
in the
work of M. P. Volarovich and E. I. Parkhomenko
[Volarovich and Parkhomenko, 1954].
The nature of the piezoelectric effect of polycrystals (rocks in particular) was
explained on the basis
of the piezoelectric texture theory which was developed by A. V. Shubnikov
[Shubnikov, 1946].
The first prove of the piezoelectric effect of rocks was the change of sign of the
polarized
charge at the change of the loading sign which was typical for the piezoelectric
crystals only.
Tests of polycrystalline rocks as well as single crystals of quartz by applying
compression and extension alternatively show the change of the charge sign. Upon
excitation of
the piezoelectric effect by ultrasound phase change of e sample mechanical oscillation
into
p the same change of phase of electrical oscillations
is observed.
Additional evidence for piezoelectric nature of the effect is establishing of the
inverse
piezoelectric effect which was observed when the rock sample was used as an ultrasonic
emitter;
ultrasonic oscillations were recorded when electric signal was applied to the sample.
Authors
[Nikitin and Parkhomenko, 1982;
Nikitin et al., 1981]
have developed an experimental procedure to determine the texture induced piezoelectric
effect in polycrystals. The
procedure is based on the fact that piezoelectric materials possess a regular (dictated
by
symmetry of piezoelectric properties of material) distribution of polarization charge
density over
the sample surface under the static loading (or dynamic excitation). The comparison
of
experimentally measured angular dependencies of the effect in the samples with theoretical
cross-sections of the indicative surfaces permits to ascertain the texture-induced
piezoelectric
effect and to determine the symmetry type of piezoelectric properties.

|
|
Figure 7
|
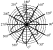
Studies containing quite new information about textures of
piezoelectrically active
samples appeared in recent years by using neutron diffraction that presents the most
comprehensive information regarding large polycrystalline samples. A sample of the
veined
quartz showing a high piezoelectric activity was analyzed in the work of
[Ivankina et al., 1991;
Walther et al., 1990].
The pole figures were measured for this sample by the time-of-flight
method on the neutron spectrometer NSHR (JINR, Dubna). The symmetry of the pole figures
was either of the sixth or third order (Figure 7).
|
|
Figure 8
|
Afterwards, angular dependencies of the piezoelectric field
(Figure 8)
were recorded by an
electrometric method using point movable electrode at ultrasonic excitation of the
sample
[Nikitin et al., 1981].
The analysis of the neutron diffraction and electrometric measurements
allowed to conclude that distribution of the pole density lines on the pole figures
is in a good
agreement with the structure and properties of the piezoelectric field of the sample.
The experimental data presented convincingly demonstrated the piezoelectric activity
of rock as
a result of its specific texture.
Some geophysicists did not accept explanation of the piezoelectric effect in rocks
based on
theory of A. V. Shubnikov. The research workers
[Tuck et al., 1977]
tried to interpret the piezoelectric properties of rocks due to presence of large
grains without
non compensated electrical charge or due to a statistic effect. J. Bishop was
the first
[Bishop, 1981]
who confirmed by experiments on the volume representative cubic samples the existence
of piezoelectric effect
due to textural features of rocks formed by minerals with piezoelectric properties.
Using the supplementary experimental studies the authors
[Ghomshei and Templeton, 1989]
examined the piezoelectric data obtained on the cubic veined quartz samples taken
from
different points of the veined surface; the results of the neutron diffraction investigation
of the
same samples were also used. Measurements of piezoelectric effect of the veined quartz
have
clearly confirmed its structural origin; the measured value was greater than the
expected
statistical effect. The texture measurements by the neutron diffraction revealed
a regular
preferred orientation of the a-axes of quartz which determines the piezoelectric
effect of the bulk
rock sample.
Explanation of physical mechanisms and processes, which lead to formation of rocks
possessing piezoelectric properties in the earth's crust under natural conditions,
is an important
and, evidently, finally unsolved problem. Three inferences were put forward about
a physical
mechanisms of the formation of piezoelectric active rocks with textures in the
[Nikitin, 1996;
Nikitin and Ivankina, 1995].
The first is related to the origination of piezoelectric properties
in the growth textures due to a phenomenal feature of quartz, namely anisotropy of
the single
quartz growth rate along the electric axes direction. Another scenario suggests that
preferred
orientations were originated in the
b -quartz under various deformation conditions
(shear or
triaxial loading) as a result of the high-temperature plastic deformation in quartz
[Walther et al., 1993a].
With temperature continuing to fall below
573o at the
b-a phase
transition to polycrystalline quartz aggregate decome piezoelectrically active. Finally,
the author
[Nikitin, 1996]
has made a supposition that piezoelectric activity of the sedimentary rock is
possible, for example, under a long-term stationary electric field within ancient
basin or due to a
source causing self-polarization of the settling piezoelectric active particles.
2.3. Textures and Magnetic Properties
All the rockforming minerals may be divided into diamagnetics, paramagnetics and
ferromagnetics. The anisotropy of magnetic susceptibility (AMS) of the bulk rock
sample is a
superposition of magnetization vectors of all the mineral components of the rock.
The degree of
anisotropy is determined by the anisotropic properties of the rock-forming minerals
[Hrouda, 1982],
shape of grains
[Uyeda et al., 1963]
and crystallographic texture of the mineral phases
[Hrouda et al., 1985].
The anisotropy of magnetic susceptibility (AMS) of material relates the magnitude
applied external magnetic field
H with the induced magnetization
M of the material by
 | (16) |
where
kij - proportionality factor which is the second-rank tensor.
The bulk susceptibility
k (k = (kmax + kmin + k
int)/3, which is determined as an arithmetic mean of the three main axes
kmax, kmin and
kint of the AMS ellipsoid, is a parameter used to represent AMS.
Parameters which are usually used to establish the AMS differ from those used for
measurement of the pole figures by diffraction methods or by some other non-magnetic
methods.
The so-called orientation tensor is employed to compare the AMS method with other
non-magnetic
methods. The main problem is in converting the magnetic susceptibility tensor into
the
orientation tensor for rocks whose magnetic anisotropy is conditioned by minerals
with the
uniaxial magnetic anisotropy (phylosilicates, hematite, pyrrhotite)
[Hrouda and Schulmann, 1990].
The method of determining the orientation tensor from the AMS is possible, provided
the
following conditions are fulfilled:
- AMS of the rock exists only due to identical minerals with a known uniaxial grain
anisotropy;
- grains of this mineral are identical in size;
- grains do not interact with magnetic fields of their own.
Consequently, the method cannot be used to determine the orientation tensor of the
rocks,
with the AMS conditioned by magnetite, as its grains reveal usually a triaxial anisotropy
(because of the grain shape effect) and the grain anisotropy extent varies from grain
to grain in
accordance with the shape variation. The method is more applicable to rocks with
the AMS
conditioned by pyrrhotite, hematite, mica or chlorite, as a magnetocrystalline anisotropy,
which
does not depend on the mineral shape and remains constant from grain to grain, is
observed in
these minerals
[Uyeda et al., 1963].
One of the most important problems of the structural geology is related to the magnetic
susceptibility source, i.e. with establishing the quantitative relation of the magnetic
structure to
the rock structure. The anisotropy of magnetic susceptibility (AMS) of the bulk rock
sample
increases notably due to presence of minerals such as magnetite, pyrrhotite or hematite.
Typical
values of the magnetic susceptibility of such ferromagnetic materials are of the
order of 5-6
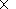 10-3 SI
volume unit. Magnetite is a mineral where the AMS depends mainly on the grain shape.
The
AMS of other ferrite minerals is controlled by the crystalline lattice type.
10-3 SI
volume unit. Magnetite is a mineral where the AMS depends mainly on the grain shape.
The
AMS of other ferrite minerals is controlled by the crystalline lattice type.
Simulation of the c-axes pole figures of the hematite rock was conducted and the
relevant
AMS-diagrams were calculated to establish interrelation between the hematite texture
and its
magnetic structure
[Siemens et al., 2000].
It turned out that quite different pictures of the
preferred orientation of the hematite c-axes are characterized by the identical magnetic
parameters. Consequently, knowledge of the AMS anisotropy of the texturized samples
does not
allow to judge the type of their crystallographic texture. Further a comparison was
made in the
paper between the experimentally measured anisotropy of the magnetic susceptibility,
hematite
pole figures assured by neutron diffraction and theoretical AMS data obtained on
the basis of the
texture analysis. The conclusion speaks about necessity to supplement a low cost
AMS
investigation method with the results of more accurate neutron diffraction or X-ray
measurements on the same geological samples so as to obtain a more comprehensive
and quality
knowledge of the magnetic properties of the texturized rocks.
The majority of the rockforming minerals are paramagnetics and diamagnetics. The
magnetic susceptibility value of the diamagnetic minerals is 1
 10-4 SI volume unit; in case
of the paramagnetic minerals this value is negative
- 1
10-4 SI volume unit; in case
of the paramagnetic minerals this value is negative
- 1
 10-5 SI volume unit.
10-5 SI volume unit.
It has been found by
Rochette, [1987]
that the crystallographic texture of the
paramagnetic minerals for rocks possessing a weak anisotropy of magnetic susceptibility
may
contribute considerably into anisotropy of magnetic properties of the bulk sample.
The texture
based calculations of the AMS were made in the paper
[Siegesmund et al., 1995],
where a quantitative relation was found between the preferred orientations of mica
and the magnetic
structure of different types of the mica-bearing rock (orthogneiss, granulite, mylonite).
A magnetic texture of the volcanic lava in the Kazbegi region (North Caucasus) has
analyzed in the paper by
[Asanidze et al., 2001].
The data cited indicate to the fact that on the
one hand the magnetic texture was formed when the lava was still moving, on the other
hand, the
NRM appeared when the stream became hard and its temperature was decreased below
the
Curie point of the magnetic minerals.
The above studies have shown that the multiphase rocks have a common problem caused
by interaction and interosculation of structures of different mineral components.
The problem
may resolved in a simple way by a selection of samples where only one mineral is
the carrier of
the AMS. However, identification of this mineral presents certain problems with other
minerals
ignored. Thus, a small quantity of neglected magnetite, which exists in numerous
types of rock,
may influence upon the investigation results. To solve this problem the samples must
be
analyzed with the altering magnetic fields to separate anisotropic components obtained
from
individual minerals. However, nothing has been mentioned in literature about such
AMS
experiments with the multiphase rocks. The problem of finding the preferred orientations
of the
main rockforming minerals with a subsequent simulation of the AMS data can be resolved
with
success using of the neutron diffraction texture analysis.
Beside of quartz and feldspar, calcite is the most essential rockforming mineral
showing
diamagnetic properties. It was shown in investigation
[de Wall et al., 2000]
that value and direction of the AMS-ellipsoid principle axes may be calculated with
a good accuracy on the
basis of the neutron diffraction measurements of the coarse-grained marble (Dubna,
Russia).
Certain difference between the calculated AMS an results of the experimental measurement
of
the magnetic susceptibility of the same samples may be due to lack of possibility
of accounting
for the grain size and grain shape during AMS simulating.
2.4. Textures and Thermal Properties of Rocks
The textures of the polycrystalline materials, formed by crystallites with a non-cubic
lattice, cause anisotropy of the thermal properties, especially thermal conductivity
and thermal
volume expansion.
The thermal conductivity of rocks belong to the main parameters which are required
for
determination of the geothermal fields. Thus, the thermal conductivity and temperature
gradient
values are used for estimation of the heat flow density in the interior of the Earth.
The thermal
conductivity of rocks in the Earth's crust depends on pressure, temperature, mineral
composition
and on the type and the fluid saturation degree.
The experimental results with the paragneiss sample extracted from the core of the
superdeeep borehole KTB may serve as an example of investigation of the texture influence
on
the thermal conductivity anisotropy
[Siegesmund, 1994].
The thermal conductivity values were
obtained for three mutually perpendicular directions at a room temperature and at
a pressure rise
up to 60 MPa. To estimate the contribution of each paragneiss mineral component
(quartz,
plagioclase and muscovite) to the meaning anisotropy of the measured thermal conductivity
was compared with the similar values of the mineral components which were calculated
by
averaging methods. The thermal conductivity of a compacted (without cracks) polycrystalline
aggregate under dry conditions depends on the thermal conductivity of the single
crystal, on the
crystallographic preferred orientation and on the volume fraction of the constituent
minerals.
The interaction of the texture-dependent thermal conductivity of quartz, mica and
plagioclase
demonstrates a complicated nature of the rock thermal conductivity. It turned out,
that
superposition of the quartz and mica textures with almost isotropic plagioclase produces
a
strong anisotropy of thermal conductivity (about 32%). The thermal conductivity data
obtained
at the time of drilling the superdeep borehole KTB support the results of simulation.
It should be noted that representation of results obtained in the work
[Siegesmund, 1994]
is insufficient. The measured quartz texture is described as weak, though the density
on the
(0001) pole figure is not given. As to sharpness of the mica texture one has only
to guess. The
numeric results on a spatial distribution of the coefficient of thermal conductivity
l, calculated
on the basis of data quartz and mica textures, are not available. Moreover, the up-to-date
methods of simulation of the physical properties permit to obtain the pattern of
the spatial
distribution of the texture-dependent property of bulk sample, are also not available
in the work
cited.
If the quantitative texture analysis of the rock samples was made in detail, computation
of
the coefficient of thermal expansion
a is possible according to the ODF data and the
a value of
single crystal. Similar simulation allows to estimate the correlation of the crystallographic
texture with the type of the thermal expansion coefficient tensor. The works about
influence of
the crystallographic texture on the thermal expansion of the natural marble samples
are well known
[Leiss and Weiss, 2000;
Siegesmund et al., 1997, 2000].
Marble as a building material has been used for over 2000 years. Buildings and other
structures made of marble are subject to a mechanical (thermal expansion/contraction
cycles)
and to a chemical weathering. These processes taken together lead to a considerable
rock
distribution. The degradation depends not only on the climatic conditions, but also
on the
mineralogical, chemical features and fabric of the rock. It has been also shown,
that the thermal
expansion of marble depends on the type and degree of the preferred orientation of
the strongly
anisotropic calcite grains
[Siegesmund et al., 1997].
Besides of the crystallographic texture the following factors influence on the thermal
properties of marble: defects of the rock fabric, grain size, grain size distribution,
grain shape,
geometry of the grain boundaries and other features of the shape texture. The marble
samples
from the Carrara, analyzed in the work by
[Widhalm et al., 1996],
have revealed a strong anisotropy of the thermal expansion, although the crystallographic
texture of these samples is not
well developed and sharp. The anisotropy of this marble is due to a strong grain
anisotropy and
to orientation of the grain boundaries.
It was confirmed by
Leiss and Weiss, [[2000]
that the spatial distribution of
the thermal expansion is controlled mainly by the texture. This was done with the
Carrara marble
samples using model calculation of the thermal expansion coefficients on the basis
of the
restored ODF. At the same time, disagreement between values of the model thermal
expansion
coefficients calculated from the crystallographic texture only and those measured
experimentally
is a result of influence of the other structural parameters and shape texture. On
this basis the
authors came to a conclusion that correlation between the crystallographic textures
and thermal
properties is not sufficient for understanding of degradation mechanismsation of
marble.
Samples of calcite-bearing rocks (similar to marble) frequently reveal a strong preferred
orientation of grains. Calcite is characterized sufficiently ductile behavior as
compared with
other minerals, therefore, the calcite-bearing rocks are a good model for the rock
deformation
experiments. The abnormal behavior of physical properties of marble caused by an
external
loading and temperatures was discovered by the authors
[Ivankina et al., 1998, 2001].
The experiments were conducted with the help of the TOF-diffractometer SKAT
equiooed with a high temperature chamber for the uniaxial compression (Dubna, Russia).
There
is a possibility to calculate from the diffraction spectra, microdeformation and
thermal
characteristics of calcite at different temperatures in the course of a mechanical
loading or
heating.
Anisotropy of the calcite thermal expansion coefficient shows itself in the difference
of the
tensor components in terms of value and sign. It is notable that only calcite and
otavite have
negative thermal expansion coefficients, while the other carbonates possess only
positive thermal
expansion coefficients.
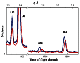
|
|
Figure 9
|
Displacements of the Bragg fabrics different in their value
were observed on the diffraction
patterns due to anisotropy of calcite at the temperature rise (Figure 9). The
greatest displacement
was recorded at the (0006) peak. It made 1.79
 10
-2 Å within the temperature
range of 20 to 220o C
that corresponded to a relative lattice deformation
Dd/d=6.20
10
-2 Å within the temperature
range of 20 to 220o C
that corresponded to a relative lattice deformation
Dd/d=6.20 10-3. The time-of-flight
diffraction spectra measured at different temperatures permitted
the spatial distribution of the
thermal expansion coefficient
a to be calculated on the basis of displacements
and relative lattice
deformations of different planes of calcite lattice. A spatial distribution of
a has an axial
10-3. The time-of-flight
diffraction spectra measured at different temperatures permitted
the spatial distribution of the
thermal expansion coefficient
a to be calculated on the basis of displacements
and relative lattice
deformations of different planes of calcite lattice. A spatial distribution of
a has an axial
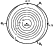
|
|
Figure 10
|
symmetry (Figure 10).
The maximum value of the main component of tensor
amax=28.25 10-6 K
-1.
Since the principle axis of the tensor coincides practically with the direction of
the normal to
the (0006) plane, difference between the minimum value of the main component of tensor
amin=-4.75
10-6 K
-1.
Since the principle axis of the tensor coincides practically with the direction of
the normal to
the (0006) plane, difference between the minimum value of the main component of tensor
amin=-4.75 10-6 K
-1 and intermediate
aint=-6.17
10-6 K
-1 and intermediate
aint=-6.17 10-6 K
-1 indicates
the experimental error which was about 5% as a result of calculation.
10-6 K
-1 indicates
the experimental error which was about 5% as a result of calculation.
2.5. Investigation of the Structure, Texture and Properties
of Meteorites
Shortly after an iron meteorite has fallen near Sterlitamak in Baskiria its fragments
were
subjected to a texture analysis
[Helming et al., 1991].
The pole figures measured presented
information about the deformation texture, which most probably occurred when a strongly
heated meteorite hit upon the Earth's surface.
The study on detection of tracks of the fast heavy nuclei was another investigation
with
the use of the neutron diffractometry aimed at determination of texture in meteorites
was
conducted in JINR (Dubna). Setting of this task is related to one of the fundamental
scientific
directions in the nuclear physics - seeking of the transuranium elements ( Z>114 ) in the primary
space substance. The work in the frame of the problem is underway for detection and
analysis of
the radiation tracks in olivines of meteorites. It is shown in papers
[Silk and Barnes, 1959;
Young, 1958]
that the natural and synthetic ionic and covalent crystals have the property of
recording and keeping the microscopic defects of structure which occur therein when
heavy
charged particles are passing through. The main parameters in the track analysis
are geometric
characteristics of tracks. The neutron diffraction texture analysis of such objects
can give a
justified conclusion about their plastic deformation and, thereby, to estimate truth
of the track
analysis results. It was found on the basis of the texture analysis of the piecies
of Maryalahti and
Eagle Station meteorites by the pole figures that there were no deformation texture
in the olivine
component of the samples
[Nikitin et al., 1999].
Interpretation of data, based on the known
physical mechanisms of the deformation texture development in olivinites, gave grounds
to
make a conclusion about a good preservation of tracks in the olivine crystals which
originated
upon decay of the uranium group nuclei.
The neutral diffractometry was used for investigation of the meteorite fragments
with the
object of finding the twinning and the orientation relationships of different phases.
The
orientation of crystallites in meteorites is observed in the process of cooling after
the phase
transitions or after a mechanical twinning caused by shock events. The microstructure
of three
nickel-iron meteorites, two hexahedrons from Walker Country (Alabama) and Coahuila
(Mexico) and one octahedron from Gibeon (Namibia) was analyzed on the basis of pole
figures
with a very narrow scanning net, comprising 7651 different orientations of the sample
[Höfler et al., 1988].
The pole figures of the BCC-kamacite (t.i. body-centered
a -Fe with less than 6% of Ni
by weight). Two types of the pole density maxima with a different intensity were
observed. The
volume content of twins is about 6% and 8% for samples from Walker Country and Coahuila
respectively. This was found from the intensity relation of the single crystal and
the twin.
Whereas the Coahuila meteorite is characterized by a symmetric maximum of the pole
density,
the Walker Country sample has a more asymmetric shape with several fuzzy extensions.
This
speaks about presence of several small pieces of kamacite with a weak distinction
of orientation
which was formed because of breakage inside the meteorite sample.
The octahedron from Gibeon was analyzed for the orientation relationships of taenite
( g -Fe with 30% of Ni by weight) and kamacite. The
taenite pole figures have shown that the taenite
rims possess a
g -phase orientation of the parent crystal. The
kamacite pole figures are
characterized by groups and belts having several intensive maxima. Orientation of
the kamacite
plates and the taenite rims is close to the Nishiyama-Wassermann relationships of
({110}a||{111}g ),
< 001 > a|| < -110 > g.
An alternative case is observed in the
kamacite crystals that can be explained by influence of deformation during the crystal
growth.
The examples of the neutron investigation of the meteorite substance point to the
fact
that a conceptual, long-term and a complex program for application of the neutron
diffraction
analysis to this field of science does not exist. Evidently, enhancement of the use
of the neutron
physics methods in cosmology might be implemented, provided the co-operation of the
Russian
and international experts on the structure and evolution of the solar system, on
meteorites and on
the neutron physics is established.
III. Use of Data on the Rock Textures in Resolving
the Problems of
Geology and Geophysics
3.1. Investigation of Metamorphic, Geodynamic and Evolutionary
Processes from Data on
Textures of Multiphase and Deep-Seated Samples
The study of structure, regularities of rocks at different levels is the fundamental
problem
of geology. One of the main tasks in the frame of this direction is the study of
regularities and
mechanisms of generation of the rock shape and crystallographic textures during magmatic,
tectonic and metamorphic processes under the thermodynamic conditions in the lithosphere.
Investigation of relations between features of the textures of different mineral
phases of
rocks and the physical-chemical mechanisms of metamorphism and other evolution processes,
will permit to approach the understanding of phenomena, that, on one hand, modify
composition, properties, state of the rocks, and on the other hand, they ensure a
striking
preservation some of their properties. The essential progress in the solution of
similar tasks was
as a result of an active application of the neutron diffraction texture analysis
in different
countries, used together with other physical and petrophysical methods
[Sobolev and Nikitin, 2001].
Till today the texture analysis of the rocks was conducted mainly on the monomineral
rocks, despite the fact that the rock is a multiphase formation, as a rule
[Mainprice and Nicolas, 1989].
The results of the neutron diffraction texture analysis of the multiphase rock (granulites
from the Low Austria) described in the paper by
[Ullemeyer and Weber, 1999],
allow the textures of some rockforming minerals (for example, quartz and biotite)
to be treated as
indicators of typical stages of the deformation history of granulites. Thus, for
example, the
predominant orientation of quartz obtained does not fit a usial coordinate system
of the sample,
which is usually connected with the schistosity directions (or "foliation-lineation'')
and with the
geographic coordinates. Similar deviations in the spatial orientation may be used
for estimation
of the direction of the large-scale horizontal shear component, which is known from
the
geological literature as the "transpressive shear vector.''
|
|
Figure 11
|
This section covers results of the complex investigation
of textures of amphibolites and
gneiss is taken from the Kola superdeep bore-hole (the depth of 8.5 to 11.5 km)
and their
analogues taken from the surface of the Pechenega geological structure. At the same
time an
attempt was made to trace the sequence of the metamorphic processes that caused the
transformation of textures. The samples taken from the depth and the surface (two
samples of
gneiss, two samples of amphibolite) exhibit identical mineral (Figure 11) and
chemical composition
and the mineral density.

|
|
Figure 12
|
Measurements of texture were made by the neutron texture
diffractometer SKAT at the
pulse reactor IBR-2. Figure 12 shows the time-of-flight diffraction spectrum of sample
K9002
gneiss. The texture analysis of such multiphase materials, composed of the low-symmetry
minerals, is not trivial as the spectra show a great number of the Bragg reflections
from
different crystallographic planes, some of which being overlapped. Nevertheless,
a sufficient
number of the experimental pole figures of plagioclase, quartz and biotite (in the
case of gneiss)
and the pole figures of the hornblende, plagioclase and quartz (in the case of amphibolites)
was
retrieved from the diffraction data.
From the set of experimental pole figures the orientation distribution functions
(ODF)
were restored for the mineral phases dominating in terms of percentage and on their
basis
calculations were made of the pole figures of the main crystallographic planes (100),
(010) and
(001) for the hornblende, plagioclase and biotite and planes (0001), (11-20) for
quartz. The
texture analysis results indicate to presence of a well developed textures of the
main rockforming
minerals.

|
|
Figure 13
|
The analysis of the texture found in the hornblende (Figure 13) permits
the assumption to be
made about existence of two stages in formation of the preffered orientations of
this mineral
component in amphibolites. Strongly correlating maxima of the main crystallographic
planes
(001), (010) and (100) are the inherent features of the first stage, whereas the
second stage is
expressed in girdle distribution of the pole density which is most clearly becomes
apparent on
the (010) PF.
The preffered orientation of the first type, was generated, evidently, at the earlier
stage
of the rock formation and is governed by a mechanism of the plastic deformation of
the
hornblende grains in the direction [001] on the planes (100). This slip system in
the hornblende
was found experimentally at 600-750o C and at the hydrostatic pressure
of 10 kbar. The next
stage of evolution of texture which produced the orientation girdles on the PF might
be induced,
for example, by recrystallization mechanisms.

|
|
Figure 14
|
The fact that the preffered orientation of plagioclase (Figure 14)
is more weak as compared
with the hornblende texture can be explained by its greater texture to the deformation
and
metamorphism processes. It is of interest, that a tendency to form the preffered
orientations with
a strong maximum in the center of the PF is seen on the (100) PF of all the samples.
But together
with other pole figures, having the girdle with the weak broaden peaks, the plagioclase
texture
cannot be treated only as a result of the plastic deformation by a dislocation slip.
|
|
Figure 15
|
The fact that the (001) pinacoid planes of plagioclase in the gneiss and amphibolite
samples retained their spatial preferred orientation (Figures 14, 15), may indicate in favor of a single
orientation mechanism, which generated the plagioclase textures and acted during
the geological
epoch. The twinning under the plastic deformation conditions could most likely become
such a
mechanism. The subsequent metamorphic changes in the rock under influence of the
changing
pressure and temperature parameters could transform greatly the plagioclase texture
without any
destruction and having retained "memory'' about the original stage of texture formation
as
identical orientation patterns on the (001) pole figures.
A mutual orientation of different mineral phases in the rocks
different by the mineral
composition might also, evidently, influence upon the progress of the mineral texture
transformation. The interaction of the plagioclase with the hornblende, which is
the main
amphibolite rockforming mineral and which retained a strong prefferd orientation,
has resulted in
violation and even destruction of the original orientation much greater in amphibolites
(Figure 14)
than in gneisses (Figure 15) and this reflects on the (001) pole figures. The
fact that the plagioclase
pole figures have no pronounced regular orientations may also indicate to a strong
recrystallization processes which have taken place during of evolution of the Archean
amphibolite rocks, that had more influence on the plagioclase than on the hornblende.
|
|
Figure 16
|
As there is a wide variety of the quartz textures, both in
amphibolites and in gneisses
(Figure 16),
it is very difficult to interpret the mechanisms and conditions of their generation.
Nevertheless, the texture analysis of quartz as a mineral component of the multiphase
rock, has a
lot of supplementary information regarding nature of the metamorphic processes, which
influence upon evolution of the rock under investigation. There is a notion that
the first (axial)
type of the quartz texture observed on the PF may be formed during the plastic deformation
under a plane strain deformation conditions, and the second type of orientation (unimodal)
indicates to its formation by the simple shear.
A wide variety of the quartz textures, occupying an insignificant volume in the
amphibolite samples, may be a result of a great diversity of the genetic processes
in quartz, its
polymorphism, a greater yielding to various metamorphic mechanisms. The latter transform
the
"relic'' textures of quartz which appeared at the stage of generation of the amphibolite
rock in the
way that they can completely or partially be overlapped by a latter texture or, on
the contrary,
can be eroded during the cooling of the rock as a result of the phase transition
and different types
of twinning.
The following facts were brought to light as a result of investigation of an elastic
anisotropy of the amphibolite spherical samples at high hydrostatic pressures with
the use
ultrasonic sounding
[Nikitin et al., 2001b].
The anisotropy factor falls down in the pressure range
of 0.1 up to 400 MPa for different samples from 2 to 6 times. This fact can
be explained by a
disintegration of the rock due to a decompression and a sharp cooling of the sample
taken to the
surface. The elastic wave velocity distribution throughout the range of pressures
that reflect the
nature of anisotropy, do not change practically and are caused by the hornblende
texture. Taking
into consideration the fact found earlier that the crystallographic textures of the
hornblende of
amphibolites taken from different depth and from the surface are practically identical,
it is
possible to state that the hornblende texture assigns a space-time coordinate system
of the crust
of the given geological region that remains unchanged for a long geological period.
This creates
conditions for application of the method of reconstruction of the paleotectonic stress/strain
state
from data on textures and seismic anisotropy of the amphibolite-containing blocks.
3.2. Reconstruction of Paleotectonic Stresses of the Ultrabasic
Blocks from Data on
Textures of Rocks and Seismic Anisotropy
It is known now, that majority of ultrabasic rocks belong to a spinel abyssal facies
and do not
show significant difference in chemical composition
[Genshaft, 1974;
Genshaft et al., 1978;
Grachev and Dobrzhinetskaya, 1987;
Lutz, 1974, 1975].
The xenolith ellipsoidal, elongated-angular and disk-shaped samples occur, as a rule,
on the surface
[Grachev et al., 1985].
The maximum size of xenolites (over a long axis) reach sometimes 70 cm
[Grachev and Dobrzhinetskaya, 1987;
Grachev et al., 1985].
It is well known from the laboratory experiments conducted by different authors on
deforming the olivine polycrystals at different temperatures and pressures, that
the texture
formation takes place within the temperature range of (600-900o C), (900-1300o
C),
(1300-1600o C) by different slip systems. Comparison of the PF of the
"reference'' samples with the PF
measured on the samples under investigation, permits to assess the depth where the
deformation
and texture formation processes were taken place and to appraise the thermodynamic
parameters
at the relevant depths from data of the neutron diffraction texture analysis. Experiments
of
different authors have shown that that the magmatic melt, which carries the xenoliths
upwards,
does not exert any significant influence upon their internal structure and texture
[Dal Negro et al., 1984;
Eales and March, 1983;
Fodor et al., 1977;
Grachev and Dobrzhinetskaya, 1987;
Grachev et al., 1985].
Many researchers adhere to a position that the external shape of xenoliths is
predetermined by the tectonic processes in the upper mantle and the texture type
is
predetermined by the acted stress fields
[Drubetskoi and Grachev, 1987;
Kiselev et al., 1987;
Polyakov, 1987].
Importance of this information lies in the fact that it gives grounds to use a complex
of
experimental data obtained as a result of the neutron diffraction texture analysis
and an
ultrasonic spatial detection determination of the maximum and minimum velocity of
the
longitudinal elastic waves to reconstruct a paleotectonic stress/strain state of
blocks of the
Earth's lithosphere. The experimental data on the relation of the olivine crystallographic
textures
and mechanical stress tensor, obtained from the laboratory deformation of the olivine
samples at
high pressures and temperatures and from the analysis of the grain orientations and
of the
external forms of xenoliths, can be put into the basis of the reconstruction.
It has been found that the [001] main crystallographic axes of the deformed olivines
are
oriented as a rule, parallel to elongation of xenoliths. [010] axes are oriented
parallel to the
maximum compression. Arrangement of [100] axes has a general tendency to be oriented
parallel to the axis of the maximum xenolith extension.
It is well known the results of experiments on deformation of the synthetic dunite
samples
under the uniaxial compression at 1250-1300o C and at 130-140 MPa
pressure of
[Nikolas et al., 1973].
At the same time, the preferred orientation of olivine is so, that [010] is also
oriented
along the axis of compression and axes [100] and [001] are oriented in the plane
perpendicular
to compression axis.

|
|
Figure 17
|
It has been found from a large series of samples
[Nikitin et al., 2001a],
that the coordinate system of the pole figures, measured by neutron diffraction,
is connected with
the coordinate system of the elastic tensor (with the direction of the maximum and
minimum velocity of the
elastic waves) of the sample. This means, that directions of principle axis of the
strain tensor can
be found in the coordinate system of the elastic tensor of the anisotropic sample
as is shown in
Figure 17.
Likewise the amphibolites, which outcropped from lower levels of the crust, whose
the
relic texture of the hornblende is retained and it controls the elastic anisotropy
of amphibolites, it
becomes evident, that the type of olivines texture practically did not change in
the dunites which
had exhumated from the mantle. Consequently, the seismic anisotropy of blocks has
also
underwent some insignificant changes. This permits to use an up-to-date DSS in a
complex with
a complete texture analysis of the outcropped olivine-bearing dunites.
Thus, the reconstruction of the paleotectonic stressed-strain state in the lithosphere
block
which contains dunites presumes as follows:
1. Assessment of depths of samples of the olivine-bearing rock, which outcropped
in different
regions, by a complex of methods, the neutron texture analysis included.
2. Dating of samples.
3. Directional determination of the main axes of the elastic tensor on the spherical
samples using
of ultrasonic sounding.
4. Determination of the spatial orientation of the sample on the basis of data
of the laboratory
ultrasonic measurements and of the orientation of the main vectors of the seismic
waves in the
amphibolite or dunite block which is established by the deep seismic sounding (DSS).
5. Establishing orientation of the main axes of the strain (or stress) tensor
in the coordinate
system of the tensor of the elastic properties of the sample using of the texture
data obtained by
the neutron diffractometry.
3.3. Reconstruction of Orientation of Main Axes of Strain/Stress
Tensor Based on Modeling
the Texture Formation
The relation between types of the crystallographic textures of rocks and type of
the
mechanical stress tensor has been investigated experimentally
[Kern, 1977]
and theoretically
[Nikitin and Ivankina, 1986;
Sobolev and Demin, 1980].
The works mentioned above became a basis for the method of reconstruction of the
paleotectonic stress-strain state in blocks of lithosphere, which influenced upon
the texture
formation of the quartz-bearing rocks, and afterwards texture was preserved
[Nikitin et al., 1991].
The modified Taylor model, which permits to obtain the pole figures in the coordinate
system of the principal axes of the strain tensor for the given material, has been
used as the basis
for modeling of texture formation.
To texture formation simulation
[Kurtasov, 1993]
the following deformation conditions
should be specified: temperature, strain-rate tensor components, the resulting strain
and number
of crystallites on the basis of which the model ODF will be restored; parameters
of material
should be also specified: slip systems, their critical shear stresses, activation
energy, symmetry
of the crystalline lattice.
Let us consider an example of modeling the texture formation in the quartz polycrystalline
material, which deforms at a temperature exceeding
a-b transition
in quarts.
The action of the slip systems (0001)
< 1120> and
{ 1101}<1120> (basic and pyramidal
sliding planes) was taken into consideration in modeling of the high-temperature
deformation of
quartz. Aside of the above, a considerable number of other slip systems is also observed
in
quarts. It was supposed that the critical shear stresses at high temperatures (over
500o C) in these
systems exceeds considerably the critical shear stresses in the easy slip systems.
Modeling of the axial compression in quartz gives an axial texture with a maximum
near
the axis of compression on the (0001) pole figure. The crystallographic directions
lying in the
base plane tend to turn towards the tension direction. The sharpness of the basis
texture increases
monotonously with the increasing of deformation degree.
The texture simulation at a pure shear was studied for the deformation 10-6 1/sec rate, and
in this case the deformation was modeled for a group consisting of 800 crystallites
with the
initial random orientations.
At a low and medium deformation degree an intermediate texture is formed, the (0001)
poles turn to the plane perpendicular to the axis of elongation and (1010) poles
of the planes
turn to the axis of elongation. With further deformation the basic plane poles turn
to the axis of
compression and ( 1010 ) poles continue to rotate to the axis of elongation. A single-component
texture
(0001)<1010> with a distinctive hexagonal symmetry of the pole figures.
To cite an example of reconstruction of the paleodeformation for sets of the veined
quartz
samples taken from one of the quartz-ore gold deposits. The samples were taken orientically
with
respect to geological references. This permitted to bring the coordinate systems
of the pole
figures into agreement with the coordinate system of the sampling points.

|
|
Figure 18
|
The pole figures of both sets of samples were measured on
the diffractometer NSHR
(Dubna, Russia). Figure 18a shows two of the nine experimentally measured PF
(11-20) and
(11-22). The pole figures have no belts which are common for the texture at the axial
deformation.
This means that all the principal deformations of the sample differ and symmetry
of the pole
figures in the principal axes of the stationary deformation must be rhombic. Consequently,
one
transformation must symmetrize all the pole figures obtained.
Figure 18b
shows the pole figures after rotation, which minimizes deviation of the pole figure
symmetry from the orthorhombic one. The high sharpness of peaks on the pole figures
can be
explained by the fact that the rock was subjected to a great plastic strain. The
additional X-ray
investigations of the crystalline structure of two samples from the selected set
have indicated to
presence of slipbands and this indicates to a considerable plastic strain. There
were no traces of
recrystallization.
Thus, from consideration of symmetry, it is possible to determine
the directions of the
principal axes of strain. To determine relative values of the principal strain the
experimental data
must be compares with results of the computer simulation. Figure 18c shows the pole figures
obtained by the pure shear simulation at 600o C and deformation 10-10 1/sec rate. The best
comparison of the model with experiment is ensured just at these parameters. A vertical
direction
on a stereographic projection corresponds to the principle tensile deformation; there
is no
deformation in the horizontal direction and the compression component acts perpendicularity
to
the projection plain. The similar position of the pole density maxima on the experimental
and
simulation pole figures can be noted. A quality similarity of the experimental data
with the
simulation data permit to interpret the paleodeformation of two samples of veined
quartz as a
pure shear deformation.
The conditions found correspond to the plastic flow of quartz in the solid-phase
hexagonal
modification through the channel of a narrow crack. Thus, interpretation of the experimental
data
of neutron diffraction textures analysis of the oriented samples by computer simulation
of the
plastic deformation permits to reconstruct the paleodeformation scheme of the rock.
IV. Earthquake Source Theory and Neutron Investigations
of
Microstrains, Microstresses, Polymorfous Transformations in
Minerals and Rocks in a Wide Range of Temperatures and Pressures
4.1. Neutron Diffraction Investigations of the Local and
Residual Strainns and Stresses of Rocks
Arrangement of extensive studies on the earthquake prediction required for a more
deep
knowledge of the physics of the earthquake preparation. Therefore, the laboratory
experiments
on the physics of materials fracture considering the bedding conditions and specific
properties
of the rocks have been considerably expanded in many research centres. A special
attention was
paid to processes of the microcrack and macrocrack formation at the shear fracture
and to the
accompanying physical and mechanical changes of properties of the materials.
Advances in the physics of fracture, and especially, a purposeful seismological laboratory
experiment permit even now to explane of the field work results and open up new possibilities
of
forecasting studies. The level of the theory of fracture formation and concept on
the seismic
source, up-to-date laboratory experiments and the field observations, as a whole,
permit to
develop the theory of the earthquake preparation
[Kasahara, 1985;
Rais, 1982].
To understand the physics of fracture formation of such heterogeneous and anisotropic
materials as rocks, it is necessary to consider the regularity of cracking, starting
from the
mineral crystalline lattices and breaking of the atomic bonding in the grain-boundary
material
[Sobolev et al., 2001].
Application of the neutron scattering permits to measure intracrystalline strains
and
stresses in the local volumes and to investigate a strain-stress state within the
sample in three
dimensions. The following most important features of the neutron diffraction method
should be
noted:
1. A great depth of scanning the material (up to 2-3 cm for steel and up
to 10 cm for
aluminium).
2. A high spatial resolution (up to 1-2 mm in any measuring-in).
3. Using time-of-flight method allows to determine the crystallographic anisotropy
of the
intracrystalline mechanical deformations simultaneously (for different ( hkl ) planes) and to
determine, by this way, anisotropy of the elastic and strength properties of the
material.
4. In case of a multiphase material (composites, ceramics, rocks) neutrons present
information
about distribution of stresses for each phase separately.
5. Usually the deformation corresponding to the internal stresses is of the
order of
Dd/d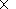 10-3-10-4,
therefore, a high resolution diffractometer is to be used for their measurement.
The shift
of the Bragg peak permits to determine strain lattice by an averaged measured volume.
The
information about microstresses (within one grain or several grains) can be obtained
from
broadening of the diffraction peaks.
10-3-10-4,
therefore, a high resolution diffractometer is to be used for their measurement.
The shift
of the Bragg peak permits to determine strain lattice by an averaged measured volume.
The
information about microstresses (within one grain or several grains) can be obtained
from
broadening of the diffraction peaks.
Advantages of the neutron diffraction method are so important that special diffractometers
were constructed in many up-to-date neutron centers in the last decade for the studying
the
intracrystalline stresses both on the steady-state reactors in Grenoble, Rzez and
Berlin, and at
the pulse neutron sources ISIS (Didcot, Chilton) and IBR-2 (Dubna).
Measurements of the intracrystalline stresses are based on determination of distance
d between the atomic planes of the crystalline lattice of the material under
investigation by a
position of the relevant Bragg peak on the spectrum. Deformation of the lattice under
stress leads
to shifting of the peak. The relative value of the shift (relative strain)
e=(d-d0)/d0,
where
d0 - interplanar spacing in the sample without internal mechanical
stresses, characterizes the
macroscopic lattice strain in the direction of the neutron scattering vector
Q which is
perpendicular to the ( hkl ) plane.
The diffractometer EPSILON, intended for investigation of the local intracrystalline
strain
and stresses has been functioning on the channel 7A of IBR-2 since 1997 in the Frank
LNP JINR
(Dubna, Russia). A good spectral resolution is attained on the spectrometer due to
a long time-of-flight
path (about 102 m). The EPSILON has two narrow diaphragm detectors, which are
arranged on opposite sides of the sample in the line perpendicular to the incident
neutron beam.
The incident beam is scattered on the interplanar bases of crystallites with the
Miller
indices ( hkl ) (in this case the Bragg law is to be fulfilled). Then, the beam
arrive at the detectors
where the neutron diffraction spectra are recorded.
The EPSILON neutron diffractometer has a miniature pressure device machine
EXSTRESS for loading of the cylindrical samples in the range of 1 up to 100 kN.
Thus, the
EPSILON can be used for measuring the residual deformations in the non-loaded samples
and
local intracrystalline strain inside the sample at different uniaxial external loads
(0.1 up to 1000 MPa).
Operation of the EPSILON diffractometer was tested on a cylindrical sample of the
Cretaceous sandstone, which was pressed through a steel tube for 20 hours after it
had been
extracted; this allowed to investigate the deformed and relaxed parts one the same
[Scheffzük et al., 1998].
For two mutually perpendicular radial directions of the cylinder the lattice spacing
are much smaller in the gripped volume than in the free volume. Despite the results
are not
interpreted finally, influence and importance of the texture in strain-stress behavior
of rocks is
obvious.
At present the EPSILON diffractometer is being updated. The purpose of this is
optimization of the neutron diffraction measurements to get a complete strain tensor.
The
updated Epsilon-MDS
[Walther et al., 2001]
comprises nine detectors arranged in a circle with
the angle of scattering for all the detectors is
2Q=90o. This means that all the
Bragg reflections
are arranged in a similar position on the diffraction patterns from each detector
and this is an
advantage of the new detector system. In this case a better spectral resolution of
3
 10-3 is
attained. The lattice strain in the diffraction experiment is measured in the direction
of the
scattering vector, which coincides with the bisector of angle between the incident
and scattered
neutron beams. By specifying this direction the polar coordinates
F and
Y, one obtains an
expression for the strain being measured
10-3 is
attained. The lattice strain in the diffraction experiment is measured in the direction
of the
scattering vector, which coincides with the bisector of angle between the incident
and scattered
neutron beams. By specifying this direction the polar coordinates
F and
Y, one obtains an
expression for the strain being measured
 | (17) |
This equation contains six unknowns. Measuring
dFY
for more than in six directions (with
respect to coordinate system of the sample), it is possible to determine the independent
components of the strain tensor
e, by solving a system of linear equations.
Measurement of strains at the other reactors are made with the help of a biaxial
powder
diffractometer equipped with large position-sensitive detectors and special sample
environment.
The diffractometer E3 at the BER-II reactor of the Hahn-Meitner Institute (Berlin)
as well as a
high-intensity variable resolution diffractometer 20 at ILL (Grenoble) belong to
this type of
instruments. These instruments are employed for analyzing the residual stresses in
the
constructional materials when the requirements in
Dd/d resolution are pronounced compared
to
the demand for the geological materials.
The best resolution can be obtained at the pulsed sources due to the time-of-flight
method. The ENGIN instrument for strain scanning is installed at the ISIS (Great
Britain)
spallation source and it functions according to the time-of-flight technique. It
is characterized by
a
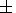 90o detector system, radial collimation
and by a possibility to measure the interplanar spacing
from 0.4 Å up to 3.3 Å. The
Dd/d resolution is of about 0,7%
on the 15 m time-of-flight path.
The gauge dimensions are 0.5
90o detector system, radial collimation
and by a possibility to measure the interplanar spacing
from 0.4 Å up to 3.3 Å. The
Dd/d resolution is of about 0,7%
on the 15 m time-of-flight path.
The gauge dimensions are 0.5
 25 mm with respect to the incident beam
in both dimensions and
1.5 mm in the scattered beam. The uniaxial loading permits to reach
25 mm with respect to the incident beam
in both dimensions and
1.5 mm in the scattered beam. The uniaxial loading permits to reach
 50 kN and it is mounted on
a position stage. Though this instrument is treated as the instrument for the engineering
investigations, it has been recently successfully used for the study of the polymineral
rocks.
Criteria for application of the instrument for investigation of the rocks may expand
considerably
due to improvement of the
Dd/d resolution and tostrain accuracy
at the new ENGIN-X beam line
with a 50 m time-of-flight path which is under construction.
50 kN and it is mounted on
a position stage. Though this instrument is treated as the instrument for the engineering
investigations, it has been recently successfully used for the study of the polymineral
rocks.
Criteria for application of the instrument for investigation of the rocks may expand
considerably
due to improvement of the
Dd/d resolution and tostrain accuracy
at the new ENGIN-X beam line
with a 50 m time-of-flight path which is under construction.
The strain partioning between the phase components in the polycrystalline calcite
+ halite
aggregates
[Rinaldi et al., 2001]
was studied on the basis of in situ deformation
experiments when the sample was subjected to different loads in the neutron beam
with the use
of the ENGIN equipment at ISIS. By determining variations in lattice parameters of
each phase
as a function of the applied load, an elastic strain of each phase was estimated
and, consequently,
its contribution into the total deformation. Measurements of calcite/halite have
revealed that the
limit of elasticity of halite is reached at the strain about of 3.50
 10
-4, and that the elastic strain
partioning between two phases is quite simple due to yelding of halite. With the
elastic strain of
calcite being more than 5.50
10
-4, and that the elastic strain
partioning between two phases is quite simple due to yelding of halite. With the
elastic strain of
calcite being more than 5.50
 10-4 the strain partioning between two phases tends to homogenous
elastic strain. Thus, the neutron diffraction strain measurements provide a possibility
to study the
elastic properties of phase components of polymineral materials and to determine
a relative
contribution of each phase into the strength properties of the rock.
10-4 the strain partioning between two phases tends to homogenous
elastic strain. Thus, the neutron diffraction strain measurements provide a possibility
to study the
elastic properties of phase components of polymineral materials and to determine
a relative
contribution of each phase into the strength properties of the rock.
4.2. Neutron Diffraction Investigation of the Rock Properties
at High Temperatures and
Under External Loads
Combination of the texture analysis and measurements of the residual and lattice
strain in
samples is the most promising direction in application of the neutron scattering
for investigation
of properties of the geological materials. Such measurements for solving the geophysical
problems become all the more important if they are conducted at different (high)
pressures,
temperatures and external loads.
The authors
[Ivankina et al., 2000]
show the first results of measurements of the calcite
lattice strain the marble, which were conducted in JINR (Dubna, Russia). The experiment
was
made on a special facility CUC (chamber for unaxial compression at high temperatures)
[Ivankina et al., 1998].
The CUC chamber is placed in the center of a mounting ring of the
SKAT spectrometer so that the sample subjected to heating compressing could be "seen''
by all
the nineteen detectors of the diffractometer simultaneously. The measuring is now
up to 650oC
and it is governed by the piston material and by permissible parameters of the temperature
piezotransducers which help to measure velocity of the ultrasonic longitudinal waves
during the
tests. A capability of changing temperature and loads (measurements of these parameters)
on the
sample directly in the neutron beam is an important feature of the design.
The neutron measurements of the lattice strain on the same marble sample under a
uniaxial compression only and under a simultaneous action of the uniaxial compression
and
temperature have shown the quite different lattice strains and stresses
[Ivankina et al., 2001].
The experimental results demonstrated the influence of temperature on behavior of
marble under load
and a principal importance of special thermoelastic properties of calcite.
The diffraction spectrum of marble was measured at the EPSILON at a room temperature
without load and then the diffraction spectra were measured in succession under external
stresses
of 25 MPa, 32 MPa and 77 MPa without heating the sample. The external
load increasing
caused the peak shift on the spectra. To direct compression in the sample, the lattice
strain of the
interplanar spacing (11-23), (10-14), (21-31) were measured and on this basis the
lattice stresses
were calculated on assumption that deformation under all external loads obeys the
Hooke's law.
The same marble sample was used for measurements of the lattice strain at the
simultaneous effects of temperature and mechanical load atn the experimental complex
SKAR-TKOS.
This experiment is described in detail in the paper
[Ivankina et al., 2001].
The time-of-flight neutron diffraction spectra were recorded at different loads and
temperatures; the relative deformations of the interplanar spacing of the crystalline
lattices and
thermal expansion coefficients were also determined. Forces on the pistons were measured
along
with recording of the diffraction spectra at the same temperatures. The macrostresses
which
increased as a result of thermal expansion of the sample was determined on the basis
of the
calibration dependence. The lattice stresses have been calculated for those temperatures
at which
the same external stresses were determined at the EPSILON (without heating).

|
|
Figure 19
|
Figure 19 shows the lattice stressed
slattice in the marble sample versus
external compression
load
smacro curves, calculated at temperatures
of 120o C, 220o C and at a room temperature for
three crystallographic directions (11-23), (10-14) and (21-31).
The lattice stresses calculated for three external compression stresses
- 25,
- 32 and
- 77 MPa
at a room temperature differ between each other depending on the crystallographic
direction and in all cases they are less than the external stresses applied to the
sample.
This can
be explained by the fact that marble is a porous rock and that at small loads the
deformation of
material is composed of the linear crystalline component of the sample and of the
nonlinear
component of the porous space.
At a simultaneous action of the mechanical load and temperature the picture is quite
different. The lattice stresses for the same crystallographic directions (11-23),
(10-14), (21-31)
differ greatly and they exceed considerably the stresses applied to the sample. This
difference
increases with the temperature rise
[Ivankina et al., 2001].
From comparison of results of the two experiments (Figure 19) one
can see that the lattice
stresses depend on the crystallographic directions: they take maximum values in the
(10-14)
direction, middle values in the (21-31) direction and minimum values in the (11-23)
direction.
The lattice stress in the (10-14) lattice direction at a temperature of 220o
C and at the
compression stress
- 32 MPa reaches the value of 162.4 MPa, that is comparable with the
compressive strength of marble (the ultimate compression strength
sc for different marbles is
in
the range of 180 to 300 MPa). The stress
slattice in the (11-23) direction
changes it sign at 220o C
with the increasing of the compression load and temperature and in the (10-14) direction
sign
changes of lattice stress occurs at a much lower temperature of 120o C.
This means that
crystallites in these lattice directions deform by tension and not by compression,
beginning from
the above indicated temperatures.
The change of sign of the lattice stresses at a continuous increasing of the external
compression and temperature can be explained by different signs of components of
the thermal
expansion tensor. At a simultaneous effect of the mechanical load, which deforms
the sample by
compression, and increasing temperature the role of the latter dominates. This means
that
deformation with a "plus'' sign for some crystallographic directions is dictated
by thermal
expansion. As may be seen from the experiment, the tensile deformation opposing to
the external
compression develops in crystallites.
Stresses capable of initiating development of microcracking must correspond to great
strains of crystallites, which are constrained inside the sample.
Reasons and conditions under which development of great local and lattice stresses
in the
rock (marble) were discussed in the paper by
[Sobolev and Nikitin, 2001].
Because there are no of rocks without of destruction as shown in these tests, it
can be assumed that those great lattice
stresses, which were calculated on the basis of the measured microstrains inside
the material. In
our case great lattice strains did not cause the stresses which were calculated according
to the
Hooke's law because of a considerable concentration of pores. The texture did not
play a
decisive role here because the neutron diffraction texture analysis of the sample
has revealed a
very weak texture.
The physical properties of the heterogenous, texturized, polycrystalline materials,
which
the rocks belong to, become apparent in different ways of the macro and micro scale
levels.
Consequently, the lattice stresses, calculated from strains measured by the neutron
diffraction
have reached the compression strength but the sample did not show any cracking after
the test
was completed.
4.3. Neutron Diffraction Investigation of Structure and
Polymorphic Transformations in
Minerals and Ice
In most cases neutron diffraction investigation is used as a for more precisevly
determing
and obtaining supplementary data about structures which were previously examined
by X-rays.
Frequently the investigation is carried out with X-ray analysis in parallel and thus,
information
about cell, symmetry and arrangement of majority of atoms are already available.
Capability of
neutrons to penetrate deeply into the substance permits to investigate the crystalline
structure at
different temperatures, pressures and other external actions which along with the
high resolution
of the neutron flux give opportunities to the researchers that were not available
earlier. A great
advantage of the neutron diffraction investigation over X-ray analysis is more precise
determination position of the light atoms in the presence the heavy atoms.
Another advantage of the neutron diffraction investigation is the possibility to
investigate
structures containing atoms with close atomic numbers which are almost indistinguishable
by X-ray.
Compounds with Ni, Fe, Co etc. may serve as an example. Amplitudes of scattering
b for
such atoms or any isotopes differ widely to determine individual positions of these
atoms.
Difference in b for isotopes of the given element permits to state the problems on
investigation
of distribution and ordering of the isotope nuclei in crystalline structures.
Neutron diffraction has an explicit advantage for determining the crystallographic
structures and transient processes in single crystals placed in various chambers.
The pecularities
of interaction of neutrons with the substance determines a typical round of experiments
on
single crystals
[Artioli, 2002]:
determination of position of light atoms and geometry of
hydrogen bonding (silica-alumina zeolites); investigation of cations partitioning
between the
crystallographic positions in minerals (albite, natrolite), what is important for
understanding the
physics and chemistry of the mineral generation.
Several examples of neutron investigations of the mineral and polymorphic formations
at
different pressures and at high and low temperatures can be cited
[Dove, 2002].
The work of
[Keen and Dove, 1998],
conducted at ISIS neutron source on observation of structure of the
silicate polymorphous states HP-tridymite,
b -crystabolite,
a -crystabolite,
b -quartz,
a -quartz at different
temperatures can be related to this type of investigations. The temperature and pressure
influence
on the structural changes, on the order-disorder phase transitions, in particular,
is studied by
powder diffraction
[Pavese, 2002].
The experiment on calcite
[Dove and Powell, 1989]
is this type of example, when order-disorder transition at 1260 K, accompanied
by change of space
group from
R 4c into
R 3m was observed. The work by
[Dove et al., 2000]
is dedicated to study of crystobolite structure at high pressure, which, as it turned
out, corresponded to a
distorted structure of high-temperature cubic
b -phase.
Of great interest are investigations conducted by a team of the French scientists
in the
Laue-Langevin Institute (Grenoble), early in the 80s
[Berge et al., 1984;
Dolino et al., 1983, 1984a, 1984b].
Results on the Bragg scattering of neutrons obtained in the work by
[Dolino et al., 1983]
conducted on a natural quartz
sample of the D10 diffractometer. When quartz was cooled from the
b -phase a weak increasing
diffuse scattering was observed around the (301) Bragg's peak, and then at a temperature
of
T(b a)+1.5 K this scattering became anisotropic and
two symmetric satellite peaks appeared,
whose intensity was rising in a linear mode along with the change of temperature.
Intensity of
satellites increased sharply at a temperature of the phase transition
T(b
a)+1.5 K this scattering became anisotropic and
two symmetric satellite peaks appeared,
whose intensity was rising in a linear mode along with the change of temperature.
Intensity of
satellites increased sharply at a temperature of the phase transition
T(b a) that corresponded to
the II kind transition. In this case appearance of an intermediate phase in the temperature
range
1.3 K over
T(b
a) that corresponded to
the II kind transition. In this case appearance of an intermediate phase in the temperature
range
1.3 K over
T(b a) was confirmed by a measurement of sample heat capacity.
The accuracy of
the neutron diffraction experiment, however, did not allow to state whether the satellite
peaks
appear exactly at a temperature of
T(b
a) was confirmed by a measurement of sample heat capacity.
The accuracy of
the neutron diffraction experiment, however, did not allow to state whether the satellite
peaks
appear exactly at a temperature of
T(b a) or this is some other anomaly.
a) or this is some other anomaly.
Subsequently the same authors fulfilled a more precise experiment (with stabilization
temperature of 0.02 K), presented in the paper
[Dolino et al., 1984b],
which is included into a cycle of articles, where results obtained from the neutron
elastic scattering
method are compared with the results of the electron-microscopy investigation. The
neutron
measurements were made on a volume quartz sample (up to several cm
3 ) and were accompanied
by a continuous measurements of thermal expansion. It was confirmed as a result of
experiments
that the
a-b quartz transformation
occurs with formation of an incommensurate phase, which
exists in a small temperature range of 1 to 2 K. The
b -quartz transition into the incommensurate
phase is continuous, the incommensurate phase -
a -quartz is the I kind transition. Noted was
also an increasing of intensity of the diffuse scattering of neutrons near the phase
transition
point. This result is in agreement with the Landau theory regarding the crystals
suffering the II
kind phase transition.
An unusual behavior of
a -quartz at high pressures has become an object
of the
experimental investigation
[Kingma et al., 1993]
with the use of a synchroton X-ray diffraction.
The test was conducted on the powder samples and on the natural quartz samples under
a static
compression. It has been found that with the increasing of pressure up to 21 GPa,
a crystallite-crystallite
metastable transition, which is observed during amorphisation in quartz. This
transition was considered as an intermediate phase in amorphisation by analogy with
the
incommensurate phase at a high-temperature
a-b transition
in quartz.
Of interest are experiments on the study of the phase transitions in molecular hydrogen
and
methane for the physics of planets. Investigation of the molecular H2 and of other molecular
systems - H2O, NH3, H2S, CH4
presents a great interest at superhigh pressures, when density of
the substance is sufficiently high that the chemical bond-site can change in thede
system. It is
assumed that at a very high pressures the molecular hydrogen H2 transforms into a metallic state
and H2O ice changes into a simple oxide with the same length of the hydrogen
bonds H-O.
Currently much attention was paid to a search of this modification of ice. These
compounds are
the main components of the crust of other planets, of Uranus and Neptune especially.
Therefore,
the structure investigations of these substances are important for understanding
the change in
interatomic relations at high densities of the substance and for the study of the
structure and
processes taking place on other planets.
The equation of the state of molecular deuterium D
2 was investigated at the DISC
diffractometer on a steady-state reactor IR-8 (RSC KI, Moscow) at pressures up to
310 kbar. The
experiments were made on the single crystalline samples with the use of magnetic
anvils. At a
compression D2 remains in the initial lattice and is close to ideal and depends but
slightly from pressure
[Glazkov et al., 1988].
The equation of state obtained differs rather greatly from of the
theoretical calculations. This testifies that estimations given by theory for pressure
at which
metallization of hydrogen takes place are far from actual values.
At present 12 modifications of ice are known and its structure was thoroughly investigated
at pressures up to 3 GPa
[Whalley et al., 1968].
However, information about the ice structure at
higher pressures was coming from the neutron diffraction measurements of the O-O
space changes
[Hemley et al., 1987]
and the empirical relations between the change of O-O and O-H
space obtained from investigation of different compounds at a normal pressure.
The texture investigation of the substance of the Moon, consisting mainly of the
rock and
ice mixture, is needed to establish its planetary history. Understanding of behavior
of ice at high
pressures and low temperatures is essential for any kind of the geological or geophysical
interpretation.
The texture of polycrystalline ice II high pressure (polymorph modification of solid
form
of water, which is stable approximately between 200 and 500 MPa and below 238 K,
rhombohedral crystal structure), which was obtained in the low-temperature experiments
at high
pressure and uniaxial compression, was studied at temperature of 77 K
[Bennett et al., 1994].
The pole figures of two deuterated samples (one was synthesized at a hydrostatic
pressure and
was shortened to 50% at 225 K, the other was obtained without hydrostatic pressure
and was
shortened by 7% at 195 K), calculated on the ODF basis show that the a-axes
align in the
direction of compression. In the polymorphous modification of the low-pressure ice
I, which
was deformed at low temperature, c-axes are oriented parallel to the direction of
compression
[Kocks et al., 1998].
It was proved by the experiments conducted at the ILL that texture in the
sample of non-deuterated ice can be measured and the ODF restored, even at a strong
incoherent
scattering of
H.
Conclusion
Many fundamental researches in various fields of geology and modern geophysics do
not
dispense now without application of neutron diffraction analysis to study of structure,
texture
and properties of geological materials as well as in simulation of the geodynamic
effects
especially at low and high temperatures and under hydrostatic and nonequiaxial pressures.
The Russian scientists from the JINR collaborating with the scientific centers of
Germany
(Institute of geology and dynamics of lithosphere of the Göttingen
University, Center of
geological investigations in Potsdam, Institute of the geological investigations
of the Kristian-Albrecht
University in Kiel) conduct systematic investigations in frames of a joint program.
A joint investigations of the physical nature of seismic anisotropy and on physics
of the
rocks fracturing are developing with the Geophysical Institute and with the Institute
of the rock
structure and mechanics of the Czech Academy of Sciences, the United Institute of
physics of
the Earth, RAS.
The number of neutron sources will be reduced early in this century as reactors whose
service life has been depleted will be taken out of service. The IBR-2 reactor at
the JINR will be
in a long outage in 2007 because of its rehabilitation. Therefore, a productive application
of
neutron diffraction for solving the problems of geology and geophysics should be
based on
improvement of efficiency and information density of experiments which are to be
selected and
conducted for the most important fundamental and applied problems of the Earth's
sciences.
The following may be place in the category of these problems:
- Classification of types of rock textures of the crust and upper mantle of the
Earth with the
purpose of clarifying knowledge about structure of lithosphere, nature of the seismic
anisotropy
and the geomechanical stability of the continental crust.
- Search of anomalous behavior the geological materials during the microstructure
transformations under the changing thermal conditions and mechanical stress fields.
- Investigation of the phase transition kineticks in different minerals and rocks
at high
thermodynamic parameters.
- Study of changes in physical properties of rocks under temperatures, mechanical
stresses
and radioactive radiation as well as of regularities of interaction of shape textures
and
crystallographic textures, which influence upon directions of movement of fluids
in the crust,
with the aim of selecting optimum materials for construction of the radioactive and
chemical
wastes storages and for estimation of risk of storing the wastes at a great depth.
- Investigation of regularities of distribution of local stresses in the texturized
rock in a
wide range of temperatures and mechanical stresses from the point of view of the
earthquake
source theory.
- Ascertainment of regularities, physical mechanisms and a chronological sequence
of the
deformation and metamorphic processes in lithosphere from a complex of geophysical,
geochemical and neutron diffraction data.
References
Activation analysis of rocks and of other objects, Collect. of articles,
Fan, Tashkent, 1967.
Adams, B. L., S. I. Wright, and K. Kunze, Orientation imaging: the emergence
of a new
microscope, Metall. Trans, 24A, 819-831, 1993.
Aksenov, V. L., Neutron physics on the threshold of the XXI century, Physics
of elementary particles and E1 (nuclei), 31, (issue 6) 1303-1342, 2000.
Aleksandrov, K. S., and G. P. Prodaivoda, Anisotropy of elastic properties of
minerals and rocks,
354 pp., Izd-vo Sib. Branch RAS, Novosibirsk, 2000.
Artioli, G., Single-crystal neutron diffraction, Eur. J. Mineral., 14, 233-239,
2002.
Asanidze, B. Z., A. V. Lomidsze, and D. M. Pechersky, Spatial orientation
of magnetic testure of
volcanic lava in Kazbegi region, Transactions of the international conference
"Physical/ chemical and petrophysical investigations in sciences about the Earth'',
pp. 7-8, Moscow, 2001.
Babuska, V., and M. Cara, Seismic anisotropy in the Earth, 217 pp.,
Kluwer Academic Publishens Dordrecht/Boston/London, 1991.
Barenblatt, G. I., et al., Kinetics of crack propagation, Eng. mag., MTT,
part 1 and 2, no. 5-6, 1966.
Bayuk, E. I., M. P. Volarovich, and F. M. Levitova, Elastic anisotropy
of rocks at high pressures,
169 pp., Nauka, Moscow, 1982.
Benn, K., and D. Mainprice, An interactive program for determination of plagioclase
crystal
axes orientations from the U-stage measurements: an aid for petrofabric studies,
Computers and Geosciences, 12, 1127-1142, 1989.
Bennett, K., H.-R. Wenk, C. S. Choi, S. F. Trevino, W. B. Durham,
and L. A. Stern, Texture
measurement at 77 K of deformed D
2 O ice II polycrystals: a study by neutron diffraction, in
Textures of geological materials, (edited by Bunge H.-J., Siegesmund S.,
Skrotski W. and
Weber K.), pp. 251-260, DGM special publication, 1994.
Bennett, K., R. B. von Dreele, and H.-R. Wenk, "HIPPO'', a new high intensity
neutron
diffractometer for characterization of bulk materials, in "Proc. ICOTOM-12'',
J. A. Szpunar,
Ed., NRC Research Press, Ottawa, Canada, vol. 1, pp.129-134, 1999.
Berge, B., G. Dolino, et al., Incommensurate phase of quartz: II. Brillouin scattering
studies, J. Physique, 45, 715-724, 1984.
Bishop, J. R., Piezoelectric effects in quartz-rich rocks, Tectonophysics, 77,
297-321, 1981.
Brokmeier, H.-G., U. Zink, R. Schnieber, and B. Witassek, TEX-2, Texture
analysis at GFSS
Research Center, Mat. Sci. Forum, 273-275, 277-282, 1998.
Bukharova, T. I., and T. I. Savelova, Application of normal distribution on
SO(3) and S
2 for
orientation distribution function approximation, Textures and Microstructures,
21, 161-176, 1993.
Bunge, H. J., Zur dartstelling allgemeiner texturen, Z. Metalkunde, 56, (2),
872-874, 1965.
Bunge, H. J., Texture analysis in material science, Mathematical methods,
330 pp., Butterworth, London. 1982.
Chateigner, D., H.-R. Wenk, and M. Pernet, Orientation distributions of low
symmetry polyphase
materials using neutron diffraction data: Application to a rock composed of quartz,
biotite
and feldspar, Textures and Microstructures, 33, 35-43, 1999.
Chekin, B. S., Effective parameters of elastic medium with random distributed cracks,
Izvestia Acad. Sci. USSR, Fizika Zemli, (4), 13-21, 1970.
Cherepanov, G. P., Propagation of cracks in continuum, PMN, 31, (3), 1967.
Dal Negro, A., S. Carbonin, C. Domeneghetti, G. M. Molin, A. Gundari,
and E. M. Picciril, Crystal
chemistry and evolution of the clynopyroxene in a suite of high-pressure ultramafic
nodules
from Newer Volcanics, Australia, Contribs, Mineral. and Petrol, 86, 221-229,
1984.
De Wall, H., M. Bestmann, and K. Ullemeyer, Anisotropy of diamagnetic susceptibility
in Thassos
marlbe: A comparison between measured and modelled data, J. Struct. Gel., 22,
1761-1771, 2000.
Dolino, G., J. P. Bachheimer, and C. M. E. Zeyen, Observation of an
intermediate phase near the
b-a transition
of quartz by heat capacity and neutron scattering measurements, Solid state comm,
45, (3), 295-299, 1983.
Dolino, G., B. Berge, et al., Incommensurate phase of quartz: I, Elastic neutron
scattering, J. Physique, 45, 361-371, 1984a.
Dolino, G., J. P. Bachheimer, et al., Incommensurate phase of quartz: III, Study
of the
coexistence state between the incommensurate and the
a -phases by neutron scattering and
electron microscopy, J. Physique, 45, 901-912, 1984b.
Dove, M. T., and B. M. Powell, Neutron diffraction study of the tricritical orientational
order/disorder phase transition in calcite at 1260 K, Phys. Chem. Minerals,
16, 503-507, 1989.
Dove, M. T., and M. S. Craig, Crystal structure of the high pressure monoclinic phase-II
of
cristobalite SiO
2, Min. Mag., 64, 569-576, 2000.
Dove, M. T., An introduction to the use of neutron scattering methods in mineral
sciences,
Eur. J. Mineral., 14, 203-224, 2002.
Drubetskoi, E. P., and A. F. Grachev, Basalts and ultrabasic xenolites of the Baikal
rift zone,
Isotopy of helium and argon. Deep xenolites and lithosphere structure, pp. 54-63,
Nauka, Moscow, 1987.
Eales, H. V., and J. S. March, Al/Cr ratios of coexisting pyroxenes and spinellides
in some
ultramafic rocks, Chem. Geol., 38, 57-74, 1983.
Fedorov, E. S., Theodolite method in geology and in petrography, 1893.
Feldmann, K., M. Betzl, W. Kleinsteuber, and K. Walther, Neutron time-of-flight
texture analysis,
Textures and Microstructures, 14-18, 59-64, 1991.
Flerov, G. N., Application of nuclear physics methods for exploration and development
of the
oil and gas fields, Radioisotopes in the Physical Sciences and Industry, Press.
Conf. Sept., Vol I, pp. 117-122, Vienna, IAEA, 1960.
Fodor, R. V., K. Keil, and G. R. Bauer, Contributions to the mineral chemistry
of Hawaiian rocks,
V, Composition and origin of ultramafic nodules and megacrysts in a Rhyodacite from
Oahu,
Hawaiian Islands, Pacif. Sci., 31, 211-222, 1977.
Genshaft, Yu. S., Experimental simulation of mineral composition of lowermost
strata of crust and of upper mantle, pp. 32-45, Nauka, Moscow, 1974.
Genshaft, Yu. S., V. A. Ermakov, and A. Ya. Saltykovsky, Construction of
regional physico-chemical
models of underground processes and of the earth crust and upper mantle structure,
Izv. Acad. Sci. USSR, Fizika Zemli, (9), 91-110, 1978.
Ghildiyal, H., E. Jansen, and A. Kirfel, Volume texture of deformed quartzite
observed with U-stage
and neutron diffractometry, Textures and Nicrostructures, 31, 239-248, 1999.
Ghomshei, M. M., and T. L. Templeton, Piezoelectric and a-axes fabric along a quartz
vein,
Phys. of the Earth and Planet. Int., 55, 374-386, 1989.
Glazkov, V. P., S. P. Besedin, I. N. Goncharenko, A. V. Irodova,
I. N. Makarenko, V. A. Somenkov,
S. M. Stishov, and S. Sh. Shilshtein, Letters to Zh. ET,
47, 661, 1988.
Grachev, A. F., V. V. Nikolaichik, and V. P. Trubytsin, About nature of
regular form and ultrabasic
xenolithes in basalts and regilarities of their size distribution, Dokl. Acad.
Sci. USSR, 285, (6), 1433-1435, 1985.
Grachev, A. D., and L. F. Dobrzhinetskaya, Structural anisotropy of the mantle
xenolithes from neogenic vulcanites of the Central Europe and its importance for
interpretation of the azimuthal seismic anisotropy of lithosphere. Deep xenolites
and lithosphere structure,
pp. 178-193, Nauka, Moscow, 1987.
Griffith, The theory of rupture, Proc. I Internat. Congr. Appl. Mech. Delff,
1924.
Hadley, K., Comparison of calculated and observed crack densities and seismic velocities
of
westerbi granite, J. Geophys. Res., 81, (20), 3484-3494, 1976.
Heilbronner, P., and C. Pauli, Interated spatial and orientation analysis of quartz
c-axes by
computer-aided microscopy, J. Struct. Geol., 15, 369-382, 1993.
Helming, K., Method of geometric approximation for a texture analysis of rocks,
Fizika Zemli, (3), 73-82, 1993.
Helming, K., and T. Eschner, A new approach to texture analysis of multiphase materials
using
a texture component model, Crystalline Research Technology, 25, K203-K208,
1990.
Helming, K., A. N. Nikitin, and K. Walther, Neutron texture investigation of
a meteor, Textures and Microstructures, 14-18, 279-283, 1991.
Hemley, R. J., A. P. Jephcoat, H. K. Mao, C. S. Zha, L. W. Finger,
and D. E. Cox, Nature, 330,737, 1987.
Hofler, S., G. Will, and H.-M. Hamm, Neutron diffraction pole figure measurements
on iron
meteorites, Earth Planet. Sci. Lett., 90, 1-10, 1988.
Holt, D. B., M. D. Muir, P. R. Grant, and I. M. Boswarva,
Quantitative scanning electron microscopy, Academic Press, New York, 1974.
Honikomb, R., Plastic deformation of metals, 408 pp., Mir, Moscow, 1972.
Hrouda, F., Magnetic anisotropy of rocks and its application in geology and geophysics,
Geophys. Surv., 5, 37-82, 1982.
Hrouda, F., H. Siemes, N. Herres, and C. Hehhig-Michaeli, The relationship
between the
magnetic anisotropy and the c-axis fabric in a massive hematite ore, J. Geophys.,
56, 174-182, 1985.
Hrouda, F., and K. Schulmann, Conversion of the magnetic susceptibility tensor into
the
orientation tensor in some rocks, Physics of the Earth and Planetary Interiors,
63, 71-77, 1990.
Jansen, E. M., H. Siemes, P. Merz, W. Schäfer,
G. Will, and M. Dahms, Determination of preferred
orientation of pyrite in a chalcopyrite ore by means of neutron diffraction,
Textures and Microstructures, 19, 203-210, 1992.
Ivankina, T. I., A. N. Nikitin, W. Voitus, and K. Walther, Texture analysis
and investigation of
piezoelectric properties of natural quartz, Textures and Microstructures, 14-18,
421-429, 1991.
Ivankina, T. I, A. N. Nikitin, K. Ullemeyer, et al., Investigation of structure
and texture
transformation processes in rocks, Schriftenr. f. Geowiss, (6), 49-56, 1998.
Ivankina, T. I., A. N. Nikitin, T. Locajicek, Z. Pros, et al., Textures
and
elastic anisotropies of amphibolites from the Kola borehole, Proceedings of the
Twelfth International Conference on Textures of Materials, vol. 2, pp. 1587-1592,
Montreal, Canada, 1999a.
Ivankina, T. I., K. Klima, T. Lokaichek, A. Nikitin, and Z. Pros,
Investigation of anisotropy of
the olivine xenolite with the help of acoustic waves and neutron diffraction,
Fizika Zemli, (5), 29-39, 1999b.
Ivankina, T. I., A. N. Nikitin, A. S. Telepnev, et al., Textures and physical
properties of marbles
deformed at 20-250o C, High Pressure Research, 17, 335-346, 2000.
Ivankina, T. I., A. N. Nikitin, A. S. Telepnev, K. Ullemeyer, G. A. Efimova,
C. M. Kireenkova,
G. A. Sobolev, V. A. Sukhoparov, and K. Walther, Influence
of temperature and a long mechanical
stress on deformation, thermal and texture characteristics of marble, Fizika
Zemli, (1), 50-65, 2001.
Kalinin, V. A., and I. O. Bayuk, Elastic anisotropy of the medium with oriented system
of cracks
with arbitrary shape and concentration, Doklad RAS, 338, (3), 1994.
Kachanov, A. N., About the crack growth kinetics, PMN, 25, (iss. 3), 1961.
Karato, S.-I., Seismic anisotropy due to lattice preferred orientation of minerals:
Kinematic or
dynamic? High-Pressure Research in Mineral Physics, pp. 455-471, Orlando.
FL: Academic Press, 1987.
Kasahara, K., Earthquake mechanics, 263 pp., Mir, Moscow, 1985.
Keen, D. A., and M. T. Dove, Local Structures of silica polymorphs, The Rutherford
Appleton Laboratory ISIS Facility Annual Report 1997-1998, pp. 44-45, 1998.
Kern, H., Preferred orientation of experimentally deformed limestone marble, quartzite
and
rock salt at different temperatures and states of stress, Tectonophysics, 39,
(1-3), 103-120, 1977.
Kingma, K. J., R. J. Hemley, Ho-kwang Mao, and D. R. Veblen, New high-pressure
transformation
in
a -quartz, Phys. Review Lett., 70, (25),
3927-3930, 1993.
Kiselev, A. I., V. G. Semenova, L. V. Solov'eva, S. V. Rasskazov,
and B. M. Vladimirov, Deep
xenolites in basalts of the Baikal rift zone and Tokin stanovik, Deep xenolites
and lithosphere structure, pp. 64-72, Nauka, Moscow, 1987.
Kocks, U. F., C. N. Tomé, and H.-R. Wenk,
Texture and anisotropy, Cambridge university press, 676 p., 1998.
Kostrov, B. V., Mechanics of the tectonic earthquake, Nauka, Moscow, 1975.
Kranz, R. I., Microcracks in Rocks, A. Review, Tectonophys., 100, (1-3),
449-480, 1983.
Kruhl, J. H., Computer-assisted determination and presentation of crystallographic
orientations
of plagioclase on the basis of universal-stage measurements, N. Jb. Miner. Abh.,
157, 185-206, 1987.
Kurtasov, S. F., Procedure of simulation of deformation textures, Factory laboratory,
59, (11), 31-34, 1993.
Leiss, B., and T. Weiss, Fabric anisotropy and its influence on physical weathering
of different
types of Carrara marbles, Journal of Structural Geology, 22, 1737-1745, 2000.
Lloyd, G. E., An appreciation of the SEM electron channeling technique for petrofabric
and
microstructural analysis of geological materials, in Textures of geological materials
(edited
by Bunge H.-J., Siegesmund S., Skrotski W. and Weber K.), pp. 93-126,
DGM special publication, 1994.
Locajicek, T., Z. Pros, K. Klima, et al., Laboratory investigation of elastic
anisotropy and
texture of rocks from Kola Super Deep Borehole SG-3, International Conference "Textures
and Physical Properties of Rocks'', Gottinger arbeiten zur geologie und palaontologie,
Gottingen, vol. 2, p. 114, 1999.
Lobanov, K. V., V. I. Kazansky, A. V. Kuznetsov, A. V. Zharikov,
A. N. Nikitin, T. I. Ivankina,
and N. V. Zamyatina, Comparison of the Archean rocks from the Kola super
deep bore hole and
their analogues from the surface by results of the structural-petrological, petrophysical
and
neutron diffraction investigations, Petrologia, (1), 30-45, 2002.
Lutterotti, L., S. Matthies, H.-R. Wenk, et al., Combined texture
and structure analysis of deformed limestone from time-of-flight neutron diffraction
spectra,
J. Appl. Phys., 81, 594-599, 1997.
Lutz, B. G., Petrology of deep zones of the continental crust and upper mantle,
304 pp., Nauka, Moscow, 1974.
Lutz, B. G., Chemical composition of the continental crust and upper mantle of
the Earth, 167 pp., Nauka, Moscow, 1975.
Mainprice, D., and A. Nicolas, Development of shape and lattice preferred orientations:
application to the seismic anisotropy of the lower crust, J. Struct. Geol., 11,
175-189, 1989.
Matthies, S., On the reproducibility of the orientation function of texture samples
from pole
figures (Ghost phenomena), Phys. Stat. Sol. (b), 92, K135-K137, 1979.
Matthies, S., G. W. Vinel, and K. Helming, Standart distribution in texture
analysis, Berlin. Acad. Verlag, vol. 1-3, 1987-1988, 1989.
Neutron-activation analysis, Coll. of articles, "Zinatne'', Riga, 1966.
Nikitin, A. N., Formation of piezoelectric textures in quartz-bearing rocks,
Fizika Zemli, (10), 15-21, 1996.
Nikitin, A. N., Anisotropy and textures of materials, Course of lectures,
Izd.. MGUMGY, 260 pp., 2000.
Nikitin, A. N., and I. K. Arkhipov, Simulation of texture formation in quartz-bearing
rocks at phase
transition temperature, Fizika Zemli, (12), 29-40, 1992.
Nikitin, A. N., and T. I. Ivankina, About connection of piezoelectric textures of
quartz with the
stressed state type, Izv. Acad. Sci. USSR, Fizika Zemli, (3), 48-57, 1986.
Nikitin, A. N., and T. I. Ivankina, On the possible mechanisms of the formation of
piezoelectric
active rocks with crystallographic textures, Textures and Microstructures, 25,
33-43, 1995.
Nikitin, A. N., and E. I. Parkhomenko, Piezoelectric textures of quartz-bearing rocks
and their
symmetric properties, Izv. Acad. Sci. USSR, Fizika Zemli, (2), 30-39, 1982.
Nikitin, A. N., et al., Measurement of angular dependences of piezoeffect in piezoactive
samples, Izv. Acad. Sci. USSR, Fizika Zemli, (12), 36-44, 1981.
Nikitin, A. N., T. I. Ivankina, and A. B. Uspenskaya, About one method
of reconstruction of
peleotectonic stresses within the tectonic block, DAS USSR, 318, (1), 168-171,
1991.
Nikitin, A. N., V. P. Perelygin, and D. E. Burylichev, Neutron diffraction
investigation of damages
in tracks of fast heavy nuclei in meteorites, Izvestia, Tulgosuniversitet. Ser.
Fizika, Iss. 2, 3-17, 1999.
Nikitin, A. N., T. I. Ivankina, D. E. Burylichev, K. Klima, T. Lokaichek,
and Z. Pros, Anisotropy and
texture of olivine-bearing mantle rocks at high pressures, Fizila Zemli,
(1), 64-78, 2001a.
Nikitin, A. N., T. I. Ivankina, K. Ullemeyer, et al., Texture controlled elastic
anisotropy of
amphibolites from the Kola superdeep borehole SG-3 at high pressure, Fizika Zemli,
(1), 41-49, 2001b.
Nicolas, A., F. Boudier, and A. M. Boullier, Mechanisms of flow in naturally
and experimentally
deformed peridotites, Amer. J. Sci., 273, 853-876, 1973.
Nikolayev, D. I., T. I. Savyolova, and K. Feldman, Approximation of the orientation
distribution of
grains in polycrystalline samples by means of Gaussian, Textures and Microstructures,
19, 9-27, 1992.
Nozik, Yu. Z., R. P. Ozerov, and K. Hennig, Neutrons and a solid body, Structural
neutronography, Vol. 1, 343 pp., Atomizdat, Moscow, 1979.
Nuclear geophysics, Coll. of articles, 560 pp., Mir, Moscow, 1964.
Ozerov, R. P., History, development and trends of neutronography, Poverhnoct',
(7), 8-19, 1997.
Pavese, A., Neutron powder diffraction and Rietveld analysis; application to crystal-chemical
studies of minerals at non-ambient conditions, Eur. J. Mineral., 14, 241-249,
2002.
Petrov, V. A., V. I. Vladimirov, and A. N. Orlov, A kinetic approach to
fracture of solids,
Phys. Stat. Sol., 42, p. 197, 1970.
Polyakov, A. I., About composition of the anomalous mantle of continental rift zones
of
Baikal and Eastern Africa, Deep xenolites and lithosphere structure, pp. 31-44,
Nauka, Moscow, 1987.
Pontecorvo, B., Neutron well logging - a new geological method based on nuclear physics,
Oil and Gas Journal, 40, 32-33, 1941.
Price, G. P., The photometric method in microstructural analysis, Am. J. Sci.,
273, 523-537, 1973.
Pros, Z., Investigation of anisotropy of elastic properties of rocks on spherical
samples at high
hydrostatic pressures, High pressure and temperature studies of physical properties
of rocks and minerals, 56 pp., Naukova Dumka, Kiev, 1977.
Rais, J. R., Earthquake focus mechanics, 217 pp., Mir, Moscow, 1982.
Rinaldi, R., G. Artioli, M. D. Dove, et al., Neutron scattering
in mineral science, earth science, and related fields with the European spallation
source
(ESS), in "Scientific Trends in Condensed Matter Research and Instrumentation
Opportunities at ESS'', Richter D., Ed., pp. 91-106, Progress Report
ESS/SAC/Report 1/01,
Forschungszentrum Julich, 2001.
Roe, R. J., Description of crystallite in polycrystalline materials, General solution
of pole
figures inversion, J. Appl. Phys., 36, (6), 2024-2031, 1965.
Rochette, P., J. Struct. Geol., 9, 1015, 1987.
Sachs, G., Zur Ableitung einer Fliessbedingung, Z. Ver. Dtsch. Ing., 72,
734-736, 1928.
Salganik, R. L., Mechanics of bodies with many cracks, Izvestia Acad. Sci. USSR,
MTT, 4, 149-158, 1973.
Sander, B., Zur Petrographisch-tektonischen Analyse, Jahrb. Geol. Bundes Anstalt.,
A23, 215, 1923.
Savelova, T. I., Functions of grain distribution by orientation and their Gaussian
approximations, Factory laboratory, 50, (5), 48-52, 1984.
Savelova, T. I., and T. I. Bukharova, Presentation of group of SU(2) and their
application. MIFI, Moscow, 1996.
Schäfer, W., Neutron diffraction applied
to geological texture and stress analysis, Eur. J. Miner., 14, 263-289, 2002.
Schäfer, W., E. Jansen, R. Skowronek,
et al., Setup and use of the ROTAX instrument at ISIS as angle-dispersive
neutron powder and texture diffractometer, Nucl. Instrum. Methods in Physics
Research A., 364, 179-185, 1995.
Scheffzük, Ch., A. Frischbutter, and K. Walther,
Intracrystalline strain measurements with time-of-flight
diffraction: Application to a Cretaceous sandstone from the Elbzone (Germany),
Schr. f. Geowiss., (6), 39-48, 1998.
Schmidt, N.-H., and N. O. Olesen, Canadian Miner., 27, 15-27,
1989.
Shemyakin, E. I., Synthetic theory of strength, Physical mezomechanics, 2,
(6), 63-69, 1999.
Shubnikov, A. V., Piezoelectric textures, 99 pp., Izd. Acad. Sci. USSR,
M-L, 1946.
Siegesmund, S., Fabric-controlled anisotropy of elastic, magnetic and thermal properties
of
rocks, in Textures of geological materials (edited by Bunge H.-J., Siegesmund S.,
Skrotski W. and Weber K.), pp. 353-379, DGM special publication, 1994.
Siegesmund, S., K. Ullemeyer, and M. Dahms, Control of rock magnetic fabrics
by mica preferred
orientation: a quantitative approach, J. Struc. Geol., 17, 1601-1613, 1995.
Siegesmund, S., A. Vollbrecht, K. Ullemeyer, T. Weiss, and R. Sobott,
Application of geological
fabric analysis for the characterization of natural building stones - case study
Kauffung
marble, International Journal for Restoration of Buildings and Monuments, 3,
269-292, 1997.
Siegesmund, S., K. Ullemeyer, T. Weiss, and E. K. Tschegg, Physical
weathering of marbles
caused by anisotropic thermal expansion, International Journal of Earth Sciences,
89, 170-182, 2000.
Siemens, H., H. Schaeben, C. A. Rosiere, and H. Quade, Crystallographic
and magnetic preferred
orientation of hematite in banded iron ores, J. Struc. Geol., 22, 1747-1759,
2000.
Silk, E. C., and R. S. Barnes, Examination of fission fragment track with an electron
microscope,
Phil. Mag., 4, 970-971, 1959.
Simmons, G., and H. Wang, Single crystal elastic constants and calculated aggregate
properties: a handbook, Cambridge, Massachusetts, 370 p., 1971.
Skrotzki, W., Mechanisms of texture development in rocks, Textures of geological
materials,
Informationsgesellschaft, Verlag, pp. 167-186, 1994.
Sobolev, G. A., Fundamentals of the earthquake forecast, 312 pp., Nauka,
Moscow, 1993.
Sobolev, G. A., and V. N. Demin, Mechanoelectric phenomena in the Earth,
215 pp., Nauka, Moscow, 1980.
Sobolev, G. A., and A. N. Nikitin, Neutronography in geophysics, Physics of elementary
particles and of atomic nucleus, 32, (6), 1359-1404, 2001.
Sobolev, G. A., A. N. Nikitin, T. I. Savelova, and V. B. Yakovlev,
Experimentally-theoretic
approach to investigation of micro- and macroproperties and state of rocks (feasible
direction
of development of the earthquake focus models), Fizika Zemli, (1), 6-15,
2001.
Stavrogin, A. N., Investigation of limiting states and deformations of rocks,
Izvestia Acad. Sci. USSR. Fizika Zemli, (12). 1969.
Steinnes, E., Epithermal neutron activation analysis of geological material,
Activation analysis in geochemistry and cosmochemistry (Brunfelt A. O.,
Steinnes E., eds.), Universitetsforlaget,
pp. 113-128, Oslo, 1977.
Taylor, G. I., Plastic strain in metals, J. Inst. Met., 62, 307-324, 1938.
Tectonophysics and mechanical properties of rocks, 195 pp., Nauka, Moscow,
1971.
Tuck, G., F. D. Stacy, and K. A. Starkey, A search for the piezoelectric
effect in quartz-bearing
rocks, Tectonophysics, 39, T17-T11, 1977.
Ullemeyer, K., and K. Weber, Lattice preferred orientation as an indicator of a complex
deformation history of rocks, Textures and Microstructures, 33, 45-60, 1999.
Ullemeyer, K., P. Spalthoff, J. Heinitz J., et al., The SKAT
texture diffractometer at the pulsed reactor IBR-2 at Dubna: experimental layout
and first
measurements, Nucl. Instrument Meth. Phys. Res. A, 412, (1), 1998.
Ullemeyer, K., G. Braun, M. Dahms, et al., Texture
analysis of a muscovite-bearing quartzite: a comparison of some currently used techniques,
Journal of Structural Geology, 22, 1541-1557, 2000.
Uyeda, S., M. D. Fuller, J. C. Belshe, and R. W. Girdler, Anisotropy
of magnetic susceptibility
of rocks and minerals, J. Geophys. Res., 68, 279-291, 1963.
Vaganov, P. A., Neutron-activation investigation of geochemical associations
of rare elements,
Nauka, Moscow, 1981.
Viglin, A. S., Quantitative measure of texture of polycrystalline materials Texture
function,
FTT, 2, (10), 2463-2476, 1960.
Volarovich, M. P., Mechanical properties of rocks at high pressures and their connection
with
porosity, Present-day problems of the rock mechanics, 250 pp., Leningrad.
1972.
Volarovich, M. P., E. I. Bayuk, A. I. Levykin, and I. S. Tomashevskaya,
Physico-mechanical properties of rocks and minerals at high pressures and temperatures,
222 pp., Nauka, Moscow, 1974.
Volarovich, M. P., and E. I. Parkhomenko, Piezoelectric effect of rocks, Dokl.
Acad. Sci. USSR, 90, (2), 239-242, 1954.
Walther, K., A. N. Nikitin, V. Foitus, and T. I. Ivankina, Neutron
diffraction investigation of texture
properties of quartz rocks, Izv. USSR Acad. of Sci., Fizika Zemli, (11),
78-84, 1990.
Walther, K., S. F. Kurtasov, A. N. Nikitin, and E. G. Torina,
Simulation of deformation textures in
high-temperature quartz, Fizika Zemli, (6), 45-48, 1993a.
Walther, K., N. N. Isakov, A. N. Nikitin, K. Ullemeyer,
and Y. Hainitz, Investigations of texture
structure of geological materials by diffraction method with the help of the high
resolution
neutron spectrometer in the Frank Neutron physics laboratory of UINI, Fizika
Zemli, (6), 37-44, 1993b.
Whalley, E., D. W. Davidson, and J. B. R. Health, J. Chem. Phys.,
48, 2362, 1968.
Walther, K., A. Frischbutter, and Ch. Scheffzük,
Modernisation of the time-of-flight
diffractometer EPSILON for strain measurements on geological samples, II German-Russian
User Meeting "Condensed Matter Physics with Neutrons at IBR-2'', pp. 6-12,
Dubna, April 21-25, 2001.
Wasserman, G., and I. Greven, Textures of metallic materials, 653 pp.,
Metallurgia, Moscow, 1969.
Wenk, H.-R., Preferred orientation in deformed metals and rocks: An introduction
to modern texture analysis, 610 pp., FL: Academic Press, Orlando. 1985.
Wenk, H.-R., H. Kern, W. Schaefer, and G. Will G, Comparison of neutron
and X-ray diffraction
in texture analysis of deformed carbonate rocks, J. Struct. Geol., 6, 687-692,
1984.
Wenk, H.-R., H. J. Bunge, E. Jansen, and J. Pannetier, Preferred orientation
of plagioclase - Neutron
diffraction and U-stage data, Tectonophysics, 126, 271-284, 1986.
Wenk, H.-R., S. Matthies, and L. Lutterotti, Texture analysis from diffraction
spectra, Materials Science Forum, 157-162, pp. 473-480, 1994.
White, H., Geological significance of recovery and recrystallization processes in
quartz,
Tectonophysics, 39, 143-170, 1977.
Widhalm, C., E. Tshegg, and W. Eppensteiner, Anisotropic thermal expansion causes
deformation
of marble cladding, Journal of Performance of Constructed Facilities, ASCE, 10,
5-10, 1996.
Will, G., P. Merz, W. Schafer, and M. Dahms, Application of position sensitive
detectors for
neutron diffraction textute analysis of hematite ore, Advanced in X-ray Analysis,
33, 277-283, 1990.
Young, D., Etching of radiation damage in litium fluorid, Nature, 182, 357-377,
1958.
Zhurkov, S. N., Kinetic concept of strength of solid bodies, Vestnik Acad. Sci.
USSR, (3), 1968.
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.1.3) on November 22, 2003.
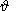 = 0o) displays red color of the
1st order.
During clockwise rotation the interference colors change:
j = 45o - blue,
j = 90o - red,
j = 135o - yellow,
j = 180o - red. During the complete
revolution this sequence repeated twice. The
increase of inclination angle and shifts of the c-axis reduce the color contrast
the blue and yellow
towards the red color of the 1st order up to an extreme case, when the c-axis becomes
perpendicular to a plane of the thin part of the section (at
= 0o) displays red color of the
1st order.
During clockwise rotation the interference colors change:
j = 45o - blue,
j = 90o - red,
j = 135o - yellow,
j = 180o - red. During the complete
revolution this sequence repeated twice. The
increase of inclination angle and shifts of the c-axis reduce the color contrast
the blue and yellow
towards the red color of the 1st order up to an extreme case, when the c-axis becomes
perpendicular to a plane of the thin part of the section (at
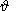 = 90o the grain shows the red
color
irrespective of angle
j ).
= 90o the grain shows the red
color
irrespective of angle
j ).

 ,
,
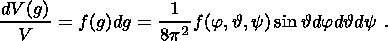
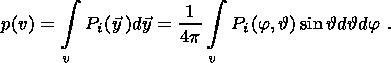
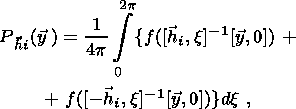
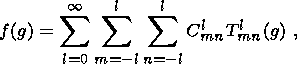
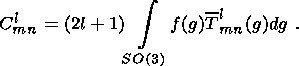
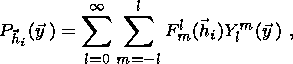
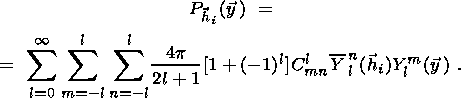
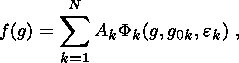
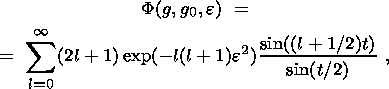
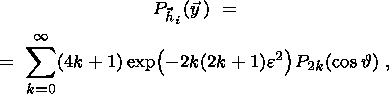
 g0 y).
Functions (11) and (12) can be approximated by more simple
expressions:
g0 y).
Functions (11) and (12) can be approximated by more simple
expressions:
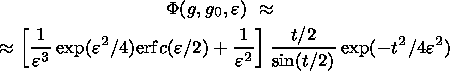
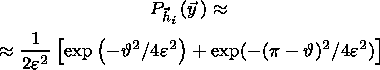


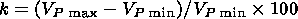





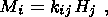
 10-3 SI
volume unit. Magnetite is a mineral where the AMS depends mainly on the grain shape.
The
AMS of other ferrite minerals is controlled by the crystalline lattice type.
10-3 SI
volume unit. Magnetite is a mineral where the AMS depends mainly on the grain shape.
The
AMS of other ferrite minerals is controlled by the crystalline lattice type.








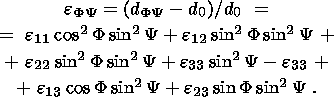
 90o detector system, radial collimation
and by a possibility to measure the interplanar spacing
from 0.4 Å up to 3.3 Å. The
Dd/d resolution is of about 0,7%
on the 15 m time-of-flight path.
The gauge dimensions are 0.5
90o detector system, radial collimation
and by a possibility to measure the interplanar spacing
from 0.4 Å up to 3.3 Å. The
Dd/d resolution is of about 0,7%
on the 15 m time-of-flight path.
The gauge dimensions are 0.5

 a)+1.5 K this scattering became anisotropic and
two symmetric satellite peaks appeared,
whose intensity was rising in a linear mode along with the change of temperature.
Intensity of
satellites increased sharply at a temperature of the phase transition
T(b
a)+1.5 K this scattering became anisotropic and
two symmetric satellite peaks appeared,
whose intensity was rising in a linear mode along with the change of temperature.
Intensity of
satellites increased sharply at a temperature of the phase transition
T(b