
A. A. Ariskin
Vernadsky Institute of Geochemistry and Analytical Chemistry, Russian Academy of Sciences
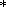 (up to ~18 wt.%) and TiO
2 (up to ~5.5 wt.%) with only minor variations in the SiO
2 contents (48 to 50 wt.%). Projection of the
compositions onto the
OLIV -
CPX -
QTZ diagram provides evidence that most of the Layered
Series crystallized on the
Ol -
Pl -
Cpx -oxide cotectic. Systematic differences between the
calculated residual liquid compositions for LZa/LZb and LZc to UZa (which are unlikely
to
reflect fractional crystallization) are within the accuracy of the COMAGMAT model,
but may
be also indicative of a late-stage process involving migration and re-equilibration
of interstitial
liquids. Estimated amounts of interstitial melts trapped in the Skaergaard "cumulates"
range
around 50 wt.%. Wager's compositions inferred from simple mass-balance were
found to lie
too far from the
Ol -
Pl -
Cpx boundary to represent a realistic approximation of the low-pressure
Skaergaard magma evolution. The main problem of genetic interpretations of the Skaergaard
intrusion is a strong misbalance between the parental compositions followed from
contact
rocks and the results of geochemical thermometry and that of the whole differentiated
body. It
is most apparent for TiO2 and P2O5 which are almost twice as high in the average intrusion
composition compared to the proposed parents. Moreover, the intrusion composition
has of 2-4 wt.%
less SiO2 and much more iron. One possible explanation is to assume the Skaergaard
magma came to the chamber with an amount of crystals ( Ol+Pl ) equilibrated with the
calculated parental liquid. However, even if some amount of "hidden" troctolitic
material
exists, it is unlikely that crystallization in a closed system could produce large
volumes of rocks
rich in Fe-Ti oxides without complementary more felsic differentiates.
(up to ~18 wt.%) and TiO
2 (up to ~5.5 wt.%) with only minor variations in the SiO
2 contents (48 to 50 wt.%). Projection of the
compositions onto the
OLIV -
CPX -
QTZ diagram provides evidence that most of the Layered
Series crystallized on the
Ol -
Pl -
Cpx -oxide cotectic. Systematic differences between the
calculated residual liquid compositions for LZa/LZb and LZc to UZa (which are unlikely
to
reflect fractional crystallization) are within the accuracy of the COMAGMAT model,
but may
be also indicative of a late-stage process involving migration and re-equilibration
of interstitial
liquids. Estimated amounts of interstitial melts trapped in the Skaergaard "cumulates"
range
around 50 wt.%. Wager's compositions inferred from simple mass-balance were
found to lie
too far from the
Ol -
Pl -
Cpx boundary to represent a realistic approximation of the low-pressure
Skaergaard magma evolution. The main problem of genetic interpretations of the Skaergaard
intrusion is a strong misbalance between the parental compositions followed from
contact
rocks and the results of geochemical thermometry and that of the whole differentiated
body. It
is most apparent for TiO2 and P2O5 which are almost twice as high in the average intrusion
composition compared to the proposed parents. Moreover, the intrusion composition
has of 2-4 wt.%
less SiO2 and much more iron. One possible explanation is to assume the Skaergaard
magma came to the chamber with an amount of crystals ( Ol+Pl ) equilibrated with the
calculated parental liquid. However, even if some amount of "hidden" troctolitic
material
exists, it is unlikely that crystallization in a closed system could produce large
volumes of rocks
rich in Fe-Ti oxides without complementary more felsic differentiates.

|
| Figure 1 |
Hunter and Sparks [1987]
used a modified version of Wager's calculations. They
emphasized that at 48.1 wt.% SiO2 in the sample
EG 4507 ( 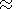 initial magma) the monotonous
silica depletion trend can not be consistent with the low SiO2 contents (44-46%) of the
observed "gabbroic assemblage"
Ol -
Pl -
Aug
initial magma) the monotonous
silica depletion trend can not be consistent with the low SiO2 contents (44-46%) of the
observed "gabbroic assemblage"
Ol -
Pl -
Aug Mt. Another discrepancy was that
the
composition at which the iron enrichment changed to silica enrichment did not coincide
with
the onset of Fe-Ti oxides crystallization in the rocks, which are known to appear
quite early in
the Skaergaard Layered Series
[McBirney, 1989;
Wager and Brown, 1967].
Following this reasoning,
Hunter and Sparks [1987]
argued that the evolution of the Skaergaard magma was
similar to that seen in differentiated tholeiitic lavas of Iceland and western Scotland.
These
speculations were supported by simple mass-balance calculations, including subtraction
of
specified amounts of the Skaergaard gabbroic components from the composition of chilled
gabbro
KT -39 assumed to present more accurate the estimate of the Skaergaard parental
magma
[Hoover, 1989].
The rhyolitic end-product was said to have been erupted without
leaving a trace in the presently exposed body of Skaergaard rocks. The geological
aspect of the
proposed interpretations found little support among petrologists who had worked on
the
intrusion and were familiar with the field relations
[Brooks and Nielsen, 1990;
McBirney and Naslund, 1990;
Morse, 1990].
They objected that Hunter and Sparks had forced the Skaergaard
liquids to follow the trend observed in volcanic rocks by assuming unrealistic volumetric
proportions and ignoring well-documented geologic evidence. This was the main reason
for
rejecting the revised direction of the Skaergaard magma fractionation, although the
phase
equilibria problems were left unresolved
[Ariskin, 1998;
Hunter and Sparks, 1990].
Mt. Another discrepancy was that
the
composition at which the iron enrichment changed to silica enrichment did not coincide
with
the onset of Fe-Ti oxides crystallization in the rocks, which are known to appear
quite early in
the Skaergaard Layered Series
[McBirney, 1989;
Wager and Brown, 1967].
Following this reasoning,
Hunter and Sparks [1987]
argued that the evolution of the Skaergaard magma was
similar to that seen in differentiated tholeiitic lavas of Iceland and western Scotland.
These
speculations were supported by simple mass-balance calculations, including subtraction
of
specified amounts of the Skaergaard gabbroic components from the composition of chilled
gabbro
KT -39 assumed to present more accurate the estimate of the Skaergaard parental
magma
[Hoover, 1989].
The rhyolitic end-product was said to have been erupted without
leaving a trace in the presently exposed body of Skaergaard rocks. The geological
aspect of the
proposed interpretations found little support among petrologists who had worked on
the
intrusion and were familiar with the field relations
[Brooks and Nielsen, 1990;
McBirney and Naslund, 1990;
Morse, 1990].
They objected that Hunter and Sparks had forced the Skaergaard
liquids to follow the trend observed in volcanic rocks by assuming unrealistic volumetric
proportions and ignoring well-documented geologic evidence. This was the main reason
for
rejecting the revised direction of the Skaergaard magma fractionation, although the
phase
equilibria problems were left unresolved
[Ariskin, 1998;
Hunter and Sparks, 1990].
An indirect way to define compositional evolution of the Skaergaard magma is to calculate perfect fractionation trajectories for a liquid thought to be parental to the whole intrusion. Recent calculations with the use of COMAGMAT-3.5 program including more accurate models for the simulation of Mt and Ilm crystallization [Ariskin and Barmina, 1999] confirme the conclusion [Ariskin et al., 1988; Toplis and Carroll, 1996] that in systems open with respect to oxygen Mt saturation leads to strongly decreasing iron and increasing silica contents of residual liquids, whereas closed systems crystallize lowered amounts of magnetite with a less pronounced iron depletion in the liquid. These simulations were conducted for two initial compositions - KT -39 [Hoover, 1989] and TM [Ariskin, 1999]. The latter is an average composition of six modeled melts assumed to be trapped in the most primitive rocks of the Marginal Border Series (Table 1). The phase equilibria calculations give evidence that both compositions are sub-cotectic ( Ol+Pl ), with KT -39 slightly oversaturated with Ol , whereas TM is closer to the Ol+Pl+Aug saturation. Liquid lines of descent representing the fractionation at 1 atm and QFM are plotted in Figure 1. Each of the initial compositions is shown by two evolutionary lines: the upper ones include calculations without any corrections in COMAGMAT-3.5, whereas the lower lines represent a corrected model, providing a maximally possible compositional shift based on the accuracy of the Mt - and Ilm -models. With these uncertainties [Ariskin, 1999] reached the following conclusions: (i) both parents exhibit only minor decrease in SiO 2 as compared to the proposed FeO-SiO 2 trend [Brooks and Nielsen, 1978, 1990; Wager and Brown, 1967]; (ii) all of the calculated trajectories indicate a well-defined inflection point, where the content of SiO 2 starts to increase due to the appearance of Mt; (iii) the maximum possible iron enrichment of residual melts is approximately 18 wt.% FeO for KT -39 and 20% for TM.
Another approach is based on the premise that the Skaergaard gabbros retained a certain amount of trapped or residual liquid within the matrix of cumulus crystals. According to the widely accepted interpretation of layered gabbros as mixtures of the primary minerals and melts, one can estimate the amount of this interstitial component from the bulk-rock concentrations of incompatible elements [e.g., Chalokwu and Grant, 1987; Henderson, 1970]. By melting a sample to a temperature slightly above to its solidus the interstitial liquid can be restored and analyzed. When this method was used to determine the composition of trapped liquid in rocks of the Layered Series [McBirney and Nakamura, 1973], at oxygen fugacities between the QFM and WM buffers and the temperatures lower 1150o C it yielded a series of compositions that follow the "Wager trend" with a steady increase in iron and no pronounced increase of silica [McBirney and Naslund, 1990]. In the FeO-SiO2 diagram this experimental trend corresponds well to that followed from some co-magmatic dike compositions (Figure 1).

|
| Figure 2 |
Utilizing the COMAGMAT-3.5 crystallization model and a modeling principle known as
"Geochemical thermometry" (Appendix A), the reconstruction of the intersitial
liquid
composition has been performed for six samples representing the least evolved part
of the
Marginal Border Series
[Ariskin, 1999].
Five of these samples were collected within 1 to 8.5 m of the intrusive contact
[Hoover, 1989],
whereas the sixth was the "chilled marginal gabbro"
EG 4507
[Wager and Brown, 1967].
Calculations of equilibrium crystallization at 1 atm
pressure, dry conditions and
QFM buffer indicated that the mineral crystallization temperatures
are correlated with the starting compositions, demonstrating a wide temperature field
of
Ol for
high-magnesia samples and an early crystallization of
Pl for a plagioclase-rich rock. Two
samples (including
EG 4507) showed sub-cotectic ( Pl+Ol ) relations in the range 1230-1250o
C.
In accordance with the sequence of crystallization, the calculated lines of descent
yielded an
obvious intersection in the range of 1175-1155oC (Figure 2). The temperature of 1165
 10oC was
accepted as representing the initial temperature of the Skaergaard parental magma.
The
average liquid composition representing this cluster of six evolutionary lines at
1165oC is given
in Table 1.
It is close to liquid compositions that
Hoover [1989]
obtained in his melting experiments with marginal rocks. In this paper, estimates
of major-element geochemistry for
"residual liquids" and primary mineral proportions for the LZ, MZ, and UZ rocks are
first
presented.
10oC was
accepted as representing the initial temperature of the Skaergaard parental magma.
The
average liquid composition representing this cluster of six evolutionary lines at
1165oC is given
in Table 1.
It is close to liquid compositions that
Hoover [1989]
obtained in his melting experiments with marginal rocks. In this paper, estimates
of major-element geochemistry for
"residual liquids" and primary mineral proportions for the LZ, MZ, and UZ rocks are
first
presented.

|
| Figure 3 |
These relations dictate the main minerals (olivine, plagioclase, augite, pigeonite, ilmenite, magnetite, and apatite) that should be included in any phase equilibria model used for the LS rocks. At present, the thermodynamic basis of COMAGMAT involves mineral-melt equilibria equations well calibrated only for the first six minerals [Ariskin and Barmina, 1999, 2000] and limits its application to LZa through UZa where apatite was not a primary phase.
Other limitations are imposed by the probable range of intensive parameters of the
crystallization. The fortuitous relations of the polymorphs of silica and Fe-rich
pyroxenes in the
Sandwich Horizon rocks allowed
Lindsley et al. [1969]
to show that that level crystallized at a
pressure of 600
 100 bars and a liquidus temperature of 970
100 bars and a liquidus temperature of 970
 20oC. Judging from the densities
of the overlying gabbros and basalts, this corresponds to a depth of about 2 km
for the
Sandwich Horizon and places LZa ~4.5 km and UZa ~3 km below the original
surface
[McBirney, 1996].
It indicates an initial pressure of ~1.3 kbar for the LZa and ~0.9 kbar
at the
boundary between MZ to UZ. For such low pressures COMAGMAT has been shown to
produce accurate phase equilibria calculations
[Ariskin, 1999;
Yang et al., 1996].
20oC. Judging from the densities
of the overlying gabbros and basalts, this corresponds to a depth of about 2 km
for the
Sandwich Horizon and places LZa ~4.5 km and UZa ~3 km below the original
surface
[McBirney, 1996].
It indicates an initial pressure of ~1.3 kbar for the LZa and ~0.9 kbar
at the
boundary between MZ to UZ. For such low pressures COMAGMAT has been shown to
produce accurate phase equilibria calculations
[Ariskin, 1999;
Yang et al., 1996].
Estimates of redox conditions during crystallization are based on mineral equilibria calculations, electrochemical measurements, and results of melting experiments. Thermodynamic calculations for quartz-fayalite-magnetite and magnetite-ilmenite equilibria indicate that the oxygen fugacity at the base of LZa was slightly above QFM [Frost and Lindsley, 1992; Morse et al., 1980; Williams, 1971] and declined towards MZ, followed by a sharp decrease at UZ which results in as much as QFM -2 at the Sandwich Horizon [Frost et al., 1988]. Although Fe-Ti oxides were shown not to have preserved their original magmatic compositions, these estimates are in fairly good aggreement with indirect evidence from experimental studies of phase relations of the natural rocks [McBirney and Naslund, 1990]. Measurements of intrinsic f O2 indicated values ranging from IW - WM [Sato and Valenza, 1980] to 0.5-1.5 units above the QFM buffer [Kersting et al., 1989].
Using the compositions of Ol - Pig - Mt - Ilm assemblages from the LZc, MZ, and UZa rocks, Williams [1971] calculated "frozen" equilibria temperatures of 1150-1050oC, with the highest values representing Lower Zone. This is in general agreement with both previous estimates for the SH (970oC) and those of melting experiments indicating temperatures of 1150-1002oC for partial melts that seem to represent differentiated (residual) liquids from the UZa to UZc [McBirney and Naslund, 1990]. Melting of the chilled gabbro KT -39 [Hoover, 1989] and results of geochemical thermometry of contact rocks [Ariskin, 1999] produced closed temperatures for the initial Ol - Pl cotectics of about 1165oC. Attempts to use temperature-sensitive oxide and two-pyroxene equilibria has resulted in under-estimations of the liquidus temperatures due to significant re-equilibration during subsolidus cooling [Jang and Naslund, 2001].

|
| Figure 4 |

|
| Figure 5 |
 UZa) and the Marginal Border Series (LZc
UZa) and the Marginal Border Series (LZc
 UZa
UZa
 ) demonstrate almost simultaneous
precipitation of ilmenite and magnetite, with
Ilm crystallized slightly earlier in the LS rocks as
33 compared to MBS. Note, also, that the MBS oxide-rich types seem to have lower-temperature
assemblages than those of the Layered Series at the same crystallinity. This latter
observation seems to support ideas that the LS has been formed from a liquid that
had already
crystallized on the wall.
) demonstrate almost simultaneous
precipitation of ilmenite and magnetite, with
Ilm crystallized slightly earlier in the LS rocks as
33 compared to MBS. Note, also, that the MBS oxide-rich types seem to have lower-temperature
assemblages than those of the Layered Series at the same crystallinity. This latter
observation seems to support ideas that the LS has been formed from a liquid that
had already
crystallized on the wall.
|
| Figure 6 |
 equivalents
corresponds well to the absence of olivine within these units (Figure 3), but
the relatively early
disappearance of the mineral obtained for the UZa and UZa
equivalents
corresponds well to the absence of olivine within these units (Figure 3), but
the relatively early
disappearance of the mineral obtained for the UZa and UZa
 average compositions (Figure 5) is
inconsistent with the petrographic character of these
Ol -bearing units. This must be considered
the most significant disagreement of the calculations with the natural observations.
In an
attempt to resolve the problem we performed an additional set of 20 calculations
simulating the
course of equilibrium crystallization at closed-to-oxygen conditions, using the average
LZa,
LZb, LZc, MZ, and UZa bulk-rock compositions.
These trajectories were calculated
at
P=1 kbar
and 0.1 wt.% H2O, with the initial Fe3+/(Fe3+ +Fe2+ )
ratios in the melt ranging from 0.10 to
0.25. Some of the results are shown in Figure 6. They include comparisons of the "closed"
modal
proportions with those obtained in the "open" ( QFM ) systems. The basic relations are
presented here as a function of the total crystallinity with the amount of the residual
liquid
given as the ordinate. Such a presentation allows one to visualize the changes in
phase
proportions between the minerals and melt, as equilibrium crystallization proceeded.
average compositions (Figure 5) is
inconsistent with the petrographic character of these
Ol -bearing units. This must be considered
the most significant disagreement of the calculations with the natural observations.
In an
attempt to resolve the problem we performed an additional set of 20 calculations
simulating the
course of equilibrium crystallization at closed-to-oxygen conditions, using the average
LZa,
LZb, LZc, MZ, and UZa bulk-rock compositions.
These trajectories were calculated
at
P=1 kbar
and 0.1 wt.% H2O, with the initial Fe3+/(Fe3+ +Fe2+ )
ratios in the melt ranging from 0.10 to
0.25. Some of the results are shown in Figure 6. They include comparisons of the "closed"
modal
proportions with those obtained in the "open" ( QFM ) systems. The basic relations are
presented here as a function of the total crystallinity with the amount of the residual
liquid
given as the ordinate. Such a presentation allows one to visualize the changes in
phase
proportions between the minerals and melt, as equilibrium crystallization proceeded.
The closed system calculations indicate olivine to be a stable
phase, at least up to a
crystallinity of 80%, with the LZc and UZa equivalents characterized by a significant
increase
in the modal
Ol proportion at late stages. This is certainly correlated with the decline
of
Pig stability relative to those observed in the
QFM buffered systems (Figures 5, 6). In fact, the
dissolution of
Ol is typical of both "open" and "closed" calculations that show an inflection
in
olivine proportions just after the appearance of magnetite (the later appearance
of
Pig reinforces the dissolution). It may indicate a peritectic reaction in
the iron-enriched basaltic
systems, such as:
Ol+l Aug (
Aug ( Pig) + Mt (
Pig) + Mt ( Ilm)
Ilm) Pl . The effects of
this reaction on phase
and chemical relations have commonly been observed in phase equilibria calculations
since the end of 1980's
[Ariskin and Barmina, 2000;
Ariskin et al., 1988].
Petrological signatures of similar peritectic relations are documented in the Skaergaard
rocks as thin rims
of olivine produced by reaction between pyroxene and Fe-Ti oxides
[McBirney, 1996].
As shown in Figure 6, the
Pig field is wider in UZa than it is in UZc. It is correlated with higher
average contents
of SiO2 (~43.1 against 41.1 wt.%), even though the Upper Series rocks
are richer in FeO
(~22.5 against 21.1 wt.%, Table 2). This may be explained by: (i) a higher
activity of SiO2 in
the residual liquid, or (ii) a greater amount of residual liquid in the UZa
rocks. Results of
geochemical thermometry given below support the first explanation, but it should
be noted that
the observed reappearance of
Ol in UZa was followed closely by the disappearance of Ca-poor
pyroxene at about the same level as the appearance of greater amounts of interstitial
granophyre
[McBirney, 1996].
Pl . The effects of
this reaction on phase
and chemical relations have commonly been observed in phase equilibria calculations
since the end of 1980's
[Ariskin and Barmina, 2000;
Ariskin et al., 1988].
Petrological signatures of similar peritectic relations are documented in the Skaergaard
rocks as thin rims
of olivine produced by reaction between pyroxene and Fe-Ti oxides
[McBirney, 1996].
As shown in Figure 6, the
Pig field is wider in UZa than it is in UZc. It is correlated with higher
average contents
of SiO2 (~43.1 against 41.1 wt.%), even though the Upper Series rocks
are richer in FeO
(~22.5 against 21.1 wt.%, Table 2). This may be explained by: (i) a higher
activity of SiO2 in
the residual liquid, or (ii) a greater amount of residual liquid in the UZa
rocks. Results of
geochemical thermometry given below support the first explanation, but it should
be noted that
the observed reappearance of
Ol in UZa was followed closely by the disappearance of Ca-poor
pyroxene at about the same level as the appearance of greater amounts of interstitial
granophyre
[McBirney, 1996].
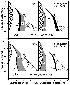
The results have an important bearing on the modal proportions of Fe-Ti oxides. The proportions of Mt calculated by COMAGMAT-3.65 in the systems closed to oxygen are two-thirds of those calculated at open conditions (Figure 6). This is not surprising, because of the effect has been demonstrated experimentally [Osborn, 1959; Presnall, 1966] and confirmed by phase equilibria calculations [Ariskin et al., 1988; Ghiorso and Carmichael, 1985; Toplis and Carroll, 1996]. A more informative approach is to analyze changes in the modal proportions of ilmenite. At closed conditions an increase in the Ilm proportion is observed, so that the bulk Ilm/Mt ratio shifts in favor of ilmenite (Figure 6). This suggests that closed-system crystallization more realistically reproduces the observed relations, since ilmenite is more abundant than magnetite in the Skaergaard rocks [McBirney, 1989]. The simultaneous crystallization of both oxides from the LZc and UZa melts may be explained from experimental results of Snyder et al. [1993]. These authors demonstrated that for a closed iron and titanium enriched system, Ilm precipitation results in the increase of Fe3+/(Fe3+ +Fe2+ ) in the melt, driving the liquid into the Mt stability field. Crystallization of magnetite has the opposite effect depleting the residual melt in Fe2O3 and lowering the relative f O2 value, so that the liquid is quickly driven into the Ilm field. The COMAGMAT calculations are also consistent with this observation (Figure 6).
|
| Figure 7 |
 contents. The rate of iron depletion
is less pronounced for
the case of the closed system owing to the lower proportion of magnetite crystallized
at closed
conditions. The amount of
Mt is limited chiefly by the bulk Fe3+/(Fe3+ +Fe2+ ) ratio of the initial
melt. In contrast, the calculations for
QFM -buffered conditions assume stepwise oxidation of
Fe2+ to Fe3+ in the melt as a result of a continual transfer of oxygen into the
crystallizing
assemblage.
contents. The rate of iron depletion
is less pronounced for
the case of the closed system owing to the lower proportion of magnetite crystallized
at closed
conditions. The amount of
Mt is limited chiefly by the bulk Fe3+/(Fe3+ +Fe2+ ) ratio of the initial
melt. In contrast, the calculations for
QFM -buffered conditions assume stepwise oxidation of
Fe2+ to Fe3+ in the melt as a result of a continual transfer of oxygen into the
crystallizing
assemblage.
I also draw attention to the percent melt shown next to the calculated trends (Figure 7). It is clear that the main objective of interest is in the range of 20 to 60% of the remaining liquid, which corresponds to the expected original modal proportions of cumulus grains (primocrysts) of 80 to 40 wt.%. For the case of the initial composition of LZc, one can see small but real differences of the iron contents of the melt at silica contents of 46 to 50 wt.% SiO2: 19-20 wt.% FeO at closed conditions and 17 to 18 wt.% at QFM. The simulations of UZa at QFM have a much wider range of liquids evolving towards somewhat unusual ferroandesitic compositions containing as much as 13 to 14 wt.% FeO at 60 wt.% SiO 2. Nevetheless, the UZa trend for closed conditions falls in a more realistic range of 47.5 to 52.5% SiO2 with 18 to 20% FeO. These results may indicate that our estimates of the differentiated liquid compositions could be best for the LZa and LZb rocks (where primocrysts of oxides are absent). If so, they could provide a good approximation for LZc (and possibly MZ) but yield an approximate composition for the UZa rocks, for which accurate estimates of the initial f O2 values and bulk Fe3+/(Fe3+ +Fe2+ ) ratios are necessary.
Thus, the preliminary calculations indicate complex relations between modal proportions of silicate and oxide minerals, residual liquid compositions, and redox conditions. In general, at relatively oxidizing conditions ( > QFM ) one would expect early precipitation and larger proportions of Mt resulting in the pronounced increase in the silica with a complementary depletion in FeO in the melt. Sharply increasing SiO 2 causes Ol dissolution to occur after the appearance of Ca-rich pyroxene and magnetite, owing to the peritectic reaction discussed above. This process is enhanced by the expansion of the Pig stability field resulting from the enrichment with SiO2 and moderation of the Mg/(Mg+Fe) ratio in the melt [Grove and Baker, 1984], leading to the disappearance of olivine at late stages. Under more reduced conditions Ilm may crystallize earlier than Mt, so that the increase in SiO2 comes relatively late. In this case the field of Pig decreases, whereas the olivine stability field increases (as the result of uncompleted Ol dissolution at the same amounts of residual liquid).
Under closed conditions, the Ol - Pig relations depend strongly on iron oxidation in the initial melt. At higher Fe3+/(Fe3+ +Fe2+ ) values, the Pig field is slightly increased because of the enrichment with SiO2 caused by earlier precipitation of magnetite. The decline of ferric iron is equivalent to melt reduction accompanied by the decrease in the Mt crystallization temperature and an expansion of the Ilm stability field (Figure 6). The general effect of closed conditions is shown to decrease the total amount of Fe-Ti oxides crystallized, so that the enrichment with SiO2 and depletion of iron becomes less pronounced (Figure 7). From the results of phase equilibria calculations one can conclude that only perfectly closed crystallization produces the predominance of Ilm over Mt observed in the LZc rocks, as well as the preservation of a part of primary Ol crystals within the Upper Zone. Note, however, the latter inference is based on the results obtained for relatively oxidized systems with a bulk Fe3+/(Fe3+ +Fe2+ )=0.15 (compare Figures 6 and 7). Judging from the liquidus temperatures (Figure 5), it corresponds to an oxygen partial pressure slightly below NNO. Thus, one should not exclude the possibility of more reduced conditions at which the liquid was depleted in SiO 2 so that Pig was not crystallized at the late stage, whereas Ol continued to crystallize in the Upper Zone.
Geochemical thermometry is a computer-based technique designed to extract initial temperature, interstitial liquid composition, primocryst mineral compositions and modal proportions, as "recorded" in the whole-rock chemistry [Frenkel et al., 1988a, 1988b]. This approach is based on interpretations of the results of phase equilibria calculations for igneous rocks and their "parents" using the COMAGMAT magma crystallization model [Ariskin, 1999], see Appendix A. Several varieties of geochemical thermometry have been proposed with the purpose to evaluate the original temperature, crystallinity and liquid composition for intrusive magmas at an initial stage corresponding to their emplacement into a magma chamber [Ariskin and Barmina, 2000]. Here the technique is applied to the Layered Series cumulates from of the Skaergaard intrusion.
A dataset of 65 bulk-rock compositions from the LZa ( n = 8), LZb (16), LZc (11), MZ (20), UZa (10) units have been selected to use in geochemical thermometry. The structural location and chemical characteristics of the samples are listed in Table 1 of McBirney [1998]. The only change is in the sample LB-238 moved from LZb to LZa. In addition, five average bulk-rock compositions of the principal units of the Layered Series and five average compositions of equivalent rocks of the Marginal Border Series were used (Table 2).
As was shown in the previous paragraph, the calculations for a system closed to O 2 seem to be more suitable if one tries to reproduce both the naturally observed modal mineral proportions and corresponding differentiated melt compositions. To conduct the closed system calculations for the Skaergaard rocks, I decided to use the bulk-rock FeO and Fe2O3 contents as a starting point for each of the above selected samples. This decision is based on the premise that most of the Skaergaard rocks are remarkably fresh and show little if any secondary oxidation. It allows one to assume that the phase equilibria simulations with the initial FeO and Fe2O3 contents may result in the intrinsic magmatic Fe3+/(Fe3+ +Fe2+ ) ratios in the residual liquids, providing a means of estimating redox conditions during differentiation.
To make sure that such calculations realistically reproduce both the original melt-mineral proportions and the residual liquid compositions we first calculated phase relations for 11 of the LZc rocks for which modal mineral proportions were available, see Table 3 of McBirney [1998]. Part of these data including those for Ilm and Mt is listed in Table 4. This tabulation also includes initial TiO2, FeO and Fe2O3 contents in the LZc rocks with the normative proportions of the oxides calculated on the assumption that Ilm and Mt are pure end-members (FeTiO3 and Fe3O4 ).
Results of phase equilibria calculations for the same LZc rocks are given in Table 4 in the form of modeled modal proportions at given amounts of crystallinity and chemical compositions (TiO2, FeO, Fe2O3 ) of the complementary residual liquids for each sample. The calculations for conditions of closed O2 were carried out at total pressure P=1 kbar and an assumed H2O content of 0.1 wt.% in all rocks. The results permit one to calculate total proportions of Fe-Ti oxides in the "computer simulated rocks" by summation of the liquidus mineral proportions at a given system crystallinity with the normative oxide proportion in the residual liquid weighted in accordance with the modal amount of this melt. These estimates are given in two lower strings of Table 4. Comparisons with the observed modal proportions indicate that COMAGMAT-3.65 closely reproduces the final amounts of ilmenite and Ti-magnetite for all but two samples, LC-417 and LC-465.
Using compositions of eight LZa rocks to estimate starting liquids, we have calculated
the course of equilibrium crystallization up to a total crystallinity of 75 to 85%.
These
calculations were conducted at the same conditions as for the LZc rocks, with crystal
increments
Ds = 1 mole
%. For 5 of the initial compositions with MgO
> 9.5 wt.%
(LA-36, -95, -237, -401, -770) a wider temperature range was obtained for
Ol, and
Pl was the second
mineral to crystallize, followed by
Aug and in some cases
Mt, and finally by
Pig:
Ol (1322 to
1258oC)
 Pl (1237 to 1193oC)
Pl (1237 to 1193oC)
 Aug
Aug Mt
(1140 to 1110oC)
Mt
(1140 to 1110oC)
 Pig (1125 to 1110oC).
Relatively early crystallization of plagioclase and pyroxene was observed for the
most calcium-rich
sample, LA-238:
Pl (1230oC)
Pig (1125 to 1110oC).
Relatively early crystallization of plagioclase and pyroxene was observed for the
most calcium-rich
sample, LA-238:
Pl (1230oC)
 Ol (1196oC)
Ol (1196oC)
 Aug (1181oC)
Aug (1181oC)
 Mt+Pig (1120-1110oC),
whereas the most silica-rich sample, LA-753 (51 wt.% SiO
2 ) indicated sub-cotectic
relations:
Ol+Pl (1210 to 1200oC)
Mt+Pig (1120-1110oC),
whereas the most silica-rich sample, LA-753 (51 wt.% SiO
2 ) indicated sub-cotectic
relations:
Ol+Pl (1210 to 1200oC)
 Aug (1153oC)
Aug (1153oC)
 Mt+Pig (1125 to 1115o
C).
Ilm was
found in minor amounts in three cases at the temperatures
< 1110oC. Only in the most titanium- and
iron-rich sample, LA-347, (5.8% TiO2 and 18.3%
FeO
Mt+Pig (1125 to 1115o
C).
Ilm was
found in minor amounts in three cases at the temperatures
< 1110oC. Only in the most titanium- and
iron-rich sample, LA-347, (5.8% TiO2 and 18.3%
FeO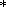 ) was
Mt the first mineral to
crystallize at 1190oC followed with
Pl (1140oC), pyroxenes and ilmenite at 1120-1110o
C.
) was
Mt the first mineral to
crystallize at 1190oC followed with
Pl (1140oC), pyroxenes and ilmenite at 1120-1110o
C.

|
| Figure 8 |
Initial mineral compositions. Calculated average
compositions of
Ol and
Pl for the six
samples at 1145oC are Fo74.9 1.5
and An66.3
1.5
and An66.3 1.9. The estimated An content in
plagioclase is in
excellent agreement with observed compositions (Figure 3), whereas the calculated
Ol composition is 7 mole % more magnesian. This difference cannot
be attributed to uncertainties
of the COMAGMAT model, which generally has an accuracy of about 1-2% Fo
[Ariskin and Barmina, 2000].
It is more likely to indicate re-equilibration of the initial olivine crystals with
an iron-enriched residual liquid constituting on average up to 50 wt.% of the
mineral-melt
assemblages (see below).
1.9. The estimated An content in
plagioclase is in
excellent agreement with observed compositions (Figure 3), whereas the calculated
Ol composition is 7 mole % more magnesian. This difference cannot
be attributed to uncertainties
of the COMAGMAT model, which generally has an accuracy of about 1-2% Fo
[Ariskin and Barmina, 2000].
It is more likely to indicate re-equilibration of the initial olivine crystals with
an iron-enriched residual liquid constituting on average up to 50 wt.% of the
mineral-melt
assemblages (see below).
Oxygen fugacity. Also shown in Figure 8 are the
T - log f O2 dependencies calculated for
each liquid line of descent as a function of the evolving Fe3+/Fe2+ ratio in the melt. These
calculations use the equation by
Sack et al. [1980]
rearranged to compute
log f O2 for a given
temperature and melt composition. As was shown by
Nikolaev et al. [1996],
such calculations have an accuracy of
 1 log unit. In ideally closed systems, the modeled
T - log f O2 trajectories
should intersect at the same temperature as the liquid compositions. In such a case,
an average
f O2 value calculated for different evolutionary lines could be considered
as an estimate of the
oxygen fugacity intrinsic to the initial mineral-melt equilibrium assemblage. For
the LZa molten
rocks these lines form a wide cluster of log
f O2 values (Figure 8) with an average of
-7.5
1 log unit. In ideally closed systems, the modeled
T - log f O2 trajectories
should intersect at the same temperature as the liquid compositions. In such a case,
an average
f O2 value calculated for different evolutionary lines could be considered
as an estimate of the
oxygen fugacity intrinsic to the initial mineral-melt equilibrium assemblage. For
the LZa molten
rocks these lines form a wide cluster of log
f O2 values (Figure 8) with an average of
-7.5 0.6 at 1145oC. This is about 1.5
log units above the
QFM buffer and is consistent with the
measurements of
Kersting et al. [1989].
Note that the standard deviations of 0.6
log units can
be attributed to both the accuracy of Sack's equation and to the analytical uncertainties
in the
bulk-rock FeO and Fe2O3 contents.
There is no reason to suspect that the COMAGMAT mass-balance
calculations for the
Ol+Pl field are incorrect
[Yang et al., 1996].
0.6 at 1145oC. This is about 1.5
log units above the
QFM buffer and is consistent with the
measurements of
Kersting et al. [1989].
Note that the standard deviations of 0.6
log units can
be attributed to both the accuracy of Sack's equation and to the analytical uncertainties
in the
bulk-rock FeO and Fe2O3 contents.
There is no reason to suspect that the COMAGMAT mass-balance
calculations for the
Ol+Pl field are incorrect
[Yang et al., 1996].
Three main crystallization sequences were found to be peculiar to the LZb rocks.
Four
trajectories (LB-104, 234, 600, and 724) indicate the order:
Ol (1370 to 1240oC)
 Pl (1220
to 1170oC)
Pl (1220
to 1170oC)
 Aug
Aug Mt
(1160 to 1110oC)
Mt
(1160 to 1110oC)
 Pig (below 1130oC); in five
cases (LB-68, 235,
269, 476, 655) augite appeared on the liquidus at temperatures of 1200 to 1170oC
simultaneously with or just after olivine, and in all seven samples plagioclase was
the first
crystallizing mineral (1250 to 1190oC) followed by
Ol and
Aug. These phase relations indicate
that
Ol and
Pl continued to be the main cotectic phases with Ca-rich pyroxene crystallizing
as
the third mineral. Ti-magnetite usually is the fourth, whereas
Pig and
Ilm were found only at
late stages at temperatures below ~1120oC and 1100oC, respectively.
These calculations are in
general agreement with petrological data indicating the change in the structural
position and
abundance of augite within the LZb horizon and do not contradict with a standard
interpretation that
Aug crystallized on a cotectic line with
Ol and
Pl [McBirney, 1989;
Wager and Brown, 1967].
Pig (below 1130oC); in five
cases (LB-68, 235,
269, 476, 655) augite appeared on the liquidus at temperatures of 1200 to 1170oC
simultaneously with or just after olivine, and in all seven samples plagioclase was
the first
crystallizing mineral (1250 to 1190oC) followed by
Ol and
Aug. These phase relations indicate
that
Ol and
Pl continued to be the main cotectic phases with Ca-rich pyroxene crystallizing
as
the third mineral. Ti-magnetite usually is the fourth, whereas
Pig and
Ilm were found only at
late stages at temperatures below ~1120oC and 1100oC, respectively.
These calculations are in
general agreement with petrological data indicating the change in the structural
position and
abundance of augite within the LZb horizon and do not contradict with a standard
interpretation that
Aug crystallized on a cotectic line with
Ol and
Pl [McBirney, 1989;
Wager and Brown, 1967].
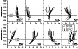
|
| Figure 9 |
 5oC: this could be accepted as the
final
equilibrium temperature at which melt was entrapped or ceased to infiltrate. The
average liquid
composition calculated for the LZb rocks at 1125oC (Table 3) is shown
in Figure 9
along with
compositions of
TM (MBS) and LZa. The liquid follows the same trend of evolution
charactered by an increase of FeO
5oC: this could be accepted as the
final
equilibrium temperature at which melt was entrapped or ceased to infiltrate. The
average liquid
composition calculated for the LZb rocks at 1125oC (Table 3) is shown
in Figure 9
along with
compositions of
TM (MBS) and LZa. The liquid follows the same trend of evolution
charactered by an increase of FeO
 at approximately constant silica contents.
at approximately constant silica contents.

|
| Figure 10 |
 2.1 ) is
slightly more calcic than the observed composition (Figure 3) but is within the accuracy of the
geothermometers used for
Pl -melt
[Ariskin, 1999].
Olivine (Fo
72.1
2.1 ) is
slightly more calcic than the observed composition (Figure 3) but is within the accuracy of the
geothermometers used for
Pl -melt
[Ariskin, 1999].
Olivine (Fo
72.1 2.1 ) becomes more ferrous
than in LZa rocks. These deviations clearly correlate with the decrease in the amount
of modal
Ol crystals in LZb rocks (Figure 10) and with the iron enrichment of the residual
liquid. It offers
indirect evidence of re-equilibration with liquids expelled from lower levels of
the Layered
Series. Modeled augites (Table 3) are also more magnesian than natural pyroxenes, although
these differences are not large (Figure 3). Again, this is consistent with earlier
observations
indicating insignificant of
Cpx re-equilibration in differentiated intrusions
[Barmina et al., 1989a].
Average proportions of interstitial material are estimated at 50
2.1 ) becomes more ferrous
than in LZa rocks. These deviations clearly correlate with the decrease in the amount
of modal
Ol crystals in LZb rocks (Figure 10) and with the iron enrichment of the residual
liquid. It offers
indirect evidence of re-equilibration with liquids expelled from lower levels of
the Layered
Series. Modeled augites (Table 3) are also more magnesian than natural pyroxenes, although
these differences are not large (Figure 3). Again, this is consistent with earlier
observations
indicating insignificant of
Cpx re-equilibration in differentiated intrusions
[Barmina et al., 1989a].
Average proportions of interstitial material are estimated at 50
 10 wt.%. The oxygen
fugacity was calculated to be similar to that of the LZa rocks with an average log
f O2 of
-7.4
10 wt.%. The oxygen
fugacity was calculated to be similar to that of the LZa rocks with an average log
f O2 of
-7.4 0.7.
0.7.
Compared to LZa and LZb, simulations for eleven LZc compositions show much more
diversity in the order of appearance of minerals on the liquidus. This is due to
the abundant
crystallization of oxides, so that for 6 samples (LC-306, 342, 465, 727, 746, and
928)
Ilm and
Mt are the first minerals to crystallize in the range of 1270 to 1170o
C. The order of
crystallization of silicate minerals for these samples is variable ( Ol Pl
Pl Aug + Pig or Ol
Aug + Pig or Ol Aug
+ Pig
Aug
+ Pig Pl ), however pyroxenes
never crystallized at temperatures above 1110oC. This
can be taken as the upper limit for the temperature controlling original mineral-melt
equilibria.
In three cases
Ol crystallized first (LC-67, 534, and 605) followed by
Pl, pyroxenes and
oxides. Sample LC-406 indicated over-saturation with plagioclase (1203oC), whereas LC-417
started with the cotectic assemblage
Ol+Pl (1157oC). These results support the notion that
Ilm and
Mt should be considered among the major primary phases of LZc
[Wager and Brown, 1967].
Pl ), however pyroxenes
never crystallized at temperatures above 1110oC. This
can be taken as the upper limit for the temperature controlling original mineral-melt
equilibria.
In three cases
Ol crystallized first (LC-67, 534, and 605) followed by
Pl, pyroxenes and
oxides. Sample LC-406 indicated over-saturation with plagioclase (1203oC), whereas LC-417
started with the cotectic assemblage
Ol+Pl (1157oC). These results support the notion that
Ilm and
Mt should be considered among the major primary phases of LZc
[Wager and Brown, 1967].
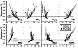
|
| Figure 11 |
 (Table 3). Both alumina and
magnesia continue to decrease, whereas a small increase in CaO is observed in the
LZc residual
liquids (Figure 11). The relative CaO enrichment is difficult
to interpret in terms of crystal
fractionation models involving simultaneous precipitation of
Pl and high-Ca pyroxene. Note,
however, the increase in calcium is certainly within the accuracy of the technique,
as indicated
by the
1s deviations for the CaO contents in the LZb
and LZc liquids (Table 3).
(Table 3). Both alumina and
magnesia continue to decrease, whereas a small increase in CaO is observed in the
LZc residual
liquids (Figure 11). The relative CaO enrichment is difficult
to interpret in terms of crystal
fractionation models involving simultaneous precipitation of
Pl and high-Ca pyroxene. Note,
however, the increase in calcium is certainly within the accuracy of the technique,
as indicated
by the
1s deviations for the CaO contents in the LZb
and LZc liquids (Table 3).
Mineral compositions of Ol, Pl, and pyroxenes equilibrated with the LZc residual liquid have the same tendency to have low amounts of the refractory components compared to the underlying mineral-melt assemblages (Table 3). Appearance of Pig crystallizing near 1100oC was observed only five times of the 11 samples, so that the question of its original primary nature in the LZc rocks is still open to question. The initial Ilm and Mt compositions are given in Table 3 in the form of the FeTiO3 and Fe2 TiO4 activities calculated using the equations of Stormer [1983]. These data indicate almost stoichiometric ilmenite and moderately titaniferous magnetite. This is consistent with a shift of the calculated f O2 values towards more reduced conditions close to the QFM buffer (Figure 11).
Twenty of the MZ samples analysed by McBirney [1998] were used in the phase equilibria calculations. Differences in the starting compositions and the extent of iron oxidation result in various crystallization sequences in which six minerals ( Ol, Pl, Aug, Pig, Ilm, Mt ) change or replace each other over small temperature intervals, often within the accuracy of the COMAGMAT model (10-15oC). Only their general features are described here. The most surprising result is that all Ol -free samples produce some amount of olivine at early and middle stages of crystallization. On average, the amount of olivine was 3 to 5 wt.% at 30% total crystallinity, but in some cases it was as much as 8 to 10 wt.% Ol. In eight samples Ol was the first mineral to crystallize at temperatures of 1190 to 1160oC (MZ-53, 55, 58, 61, 747, 824, 826, 831). However, at lower temperatures corresponding 50 to 70% crystals this olivine was completely dissolved by reaction with pyroxenes, oxides and melt. For the eight samples that contain the most TiO2 and iron (MZ-28, 172, 438, 603, 613, 729, 830, 901), Fe-Ti oxides crystallized first, followed by Ol, Pl, and pyroxenes. In four cases, the starting melts were slightly oversaturated with plagioclase at 1210 to 1160oC (MZ-99, 343, 530, 864). Note that in only two cases was Aug found at temperatures above 1105oC, whereas Pig always crystallized below 1100oC. It is important to note that in half of the samples pigeonite appeared at a total crystallinity of 20 to 40%. This may indicate that the mineral may have been among the primary crystallizing phases. In any case, a substantial amount of Pig was certainly formed at later stages by the peritectic replacement of olivine.
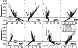
|
| Figure 12 |
Mineral compositions in Table 3 are weighted average values for
Ol, Pl, pyroxenes and
oxides at 1090oC. The modelled
Pl composition (An54.2 2.9 ) is close to the observed
plagioclase
composition of An51, while calculated pyroxenes and olivine relicts are again more magnesian.
Ilmenite became slightly richer in FeTiO3, whereas the activity of the ulvospinel component in
Ti-magnetite increased considerably ( Ulv72 in MZ versus
Ulv54 in LZc). At first view this seems
strange, because the calculated TiO2 in the melt was found to decrease somewhat. However, if
one considers the
T - log f O2 diagram (Figure 12), it is clear that within the MZ zone
the system
was evolving to more reduced conditions, slightly below
QFM (Table 3). This conclusion is in
excellent agreement with the previous thermodynamic and experimental estimates indicating
a
smooth
f O2 decline towards MZ, where redox conditions corresponded to about 0.5
log units below
QFM [Frost and Lindsley, 1992;
McBirney, 1996;
Morse et al., 1980;
Williams, 1971].
On the other hand, this somewhat surprising behavior may indicate that the initial
Fe2O3 and
FeO contents used in the closed system calculations really reflect both the total
amount of
oxides and Fe3+/Fe2+ ratios intrinsic to the MZ residual liquids. It supports the premise
that
most of the Skaergaard rocks have undergone insignificant secondary oxidation.
2.9 ) is close to the observed
plagioclase
composition of An51, while calculated pyroxenes and olivine relicts are again more magnesian.
Ilmenite became slightly richer in FeTiO3, whereas the activity of the ulvospinel component in
Ti-magnetite increased considerably ( Ulv72 in MZ versus
Ulv54 in LZc). At first view this seems
strange, because the calculated TiO2 in the melt was found to decrease somewhat. However, if
one considers the
T - log f O2 diagram (Figure 12), it is clear that within the MZ zone
the system
was evolving to more reduced conditions, slightly below
QFM (Table 3). This conclusion is in
excellent agreement with the previous thermodynamic and experimental estimates indicating
a
smooth
f O2 decline towards MZ, where redox conditions corresponded to about 0.5
log units below
QFM [Frost and Lindsley, 1992;
McBirney, 1996;
Morse et al., 1980;
Williams, 1971].
On the other hand, this somewhat surprising behavior may indicate that the initial
Fe2O3 and
FeO contents used in the closed system calculations really reflect both the total
amount of
oxides and Fe3+/Fe2+ ratios intrinsic to the MZ residual liquids. It supports the premise
that
most of the Skaergaard rocks have undergone insignificant secondary oxidation.
Phase equilibria calculations for ten LZa rocks produced
the lowest temperatures for
those parts of the Layered Series studied thus far. None of the assemblages had a
silicate
liquidus temperature above 1180oC. On average, the modeled sequences
are similar to those of
MZ (Figure 5),
starting from sub-cotectic ( Ol + Pl oxide) or compositions slightly
oversaturated with olivine (UA-102, 136, 199, 200, 300, 315, 614, 786). The two samples
with the highest FeO contents (UA-131 with 35 wt.% and UA-425 with 46 wt.%)
have a large
magnetite field and were excluded from further considerations because of strong deviations
of
their trends from those calculated for other samples. Both
pyroxenes crystallized almost
simultaneously at temperatures below 1100oC, with the
Pig crystallization interval slightly
decreased with respect to the MZ simulations. This resulted in an increase in the
modal
proportion of
Ol (Figure 10), but
Pig did not disappear completely (as can be seen in Figure 3) but
continued to be a primary phase. This corresponds observations of nature that
Pig continued
continued to present in many rocks in the lower half of UZa
[McBirney, pers. comm.].
oxide) or compositions slightly
oversaturated with olivine (UA-102, 136, 199, 200, 300, 315, 614, 786). The two samples
with the highest FeO contents (UA-131 with 35 wt.% and UA-425 with 46 wt.%)
have a large
magnetite field and were excluded from further considerations because of strong deviations
of
their trends from those calculated for other samples. Both
pyroxenes crystallized almost
simultaneously at temperatures below 1100oC, with the
Pig crystallization interval slightly
decreased with respect to the MZ simulations. This resulted in an increase in the
modal
proportion of
Ol (Figure 10), but
Pig did not disappear completely (as can be seen in Figure 3) but
continued to be a primary phase. This corresponds observations of nature that
Pig continued
continued to present in many rocks in the lower half of UZa
[McBirney, pers. comm.].
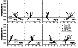
|
| Figure 13 |
Mineral compositions of the six-phase liquidus assemblage
calculated at 1085oC follow
the same trend of the depletion in the refractory components as in lower horizons
(Table 3).
The modeled plagioclase (An
48.0 3.1 ) is similar to the composition
of An
46 observed at the base
of UZa (Figure 3),
whereas the calculated
Ol (Fo52.5
3.1 ) is similar to the composition
of An
46 observed at the base
of UZa (Figure 3),
whereas the calculated
Ol (Fo52.5 2.5 ) is much more magnesian
than the
observed composition (Fo40 ). Both pyroxenes have higher
Fs/En ratios, although the modeled
augite is of 4 to 5 mole % richer in
Wo than the natural one. Although the ilmenite composition
remains unchanged, magnetite demonstrates a further increase in Fe2TiO4 (81.4
2.5 ) is much more magnesian
than the
observed composition (Fo40 ). Both pyroxenes have higher
Fs/En ratios, although the modeled
augite is of 4 to 5 mole % richer in
Wo than the natural one. Although the ilmenite composition
remains unchanged, magnetite demonstrates a further increase in Fe2TiO4 (81.4
 6.7 mole %
Ulv ).
6.7 mole %
Ulv ).
Geochemical thermometry for the Layered Series rocks produced
a probable range of the
"formation temperatures" that represent original intersitial material (Table 3). It spans
a range
of only 60oC between 1145
 10oC at LZa to 1085
10oC at LZa to 1085
 10oC at UZa. The observed values
correspond to other estimates based on other approaches
[Hoover, 1989;
Jang and Naslund, 2001;
McBirney and Naslund, 1990;
Williams, 1971].
The phase equilibria simulations also
define the range of oxygen fugacities intrinsic to the initial liquids. Our results
indicate a sharp
decline in
log f O2 values from 1 to 1.5 units above
QFM in LZa and LZb to
QFM and lower
oxygen fugacities starting from LZc. This is also in fairly good agreement with previous
estimates
[Frost and Lindsley, 1992;
Frost et al., 1988;
Kersting et al., 1989;
Lindsley et al., 1969;
Morse et al., 1980;
Williams, 1971].
10oC at UZa. The observed values
correspond to other estimates based on other approaches
[Hoover, 1989;
Jang and Naslund, 2001;
McBirney and Naslund, 1990;
Williams, 1971].
The phase equilibria simulations also
define the range of oxygen fugacities intrinsic to the initial liquids. Our results
indicate a sharp
decline in
log f O2 values from 1 to 1.5 units above
QFM in LZa and LZb to
QFM and lower
oxygen fugacities starting from LZc. This is also in fairly good agreement with previous
estimates
[Frost and Lindsley, 1992;
Frost et al., 1988;
Kersting et al., 1989;
Lindsley et al., 1969;
Morse et al., 1980;
Williams, 1971].
The main result of the geochemical thermometry is an estimate of the initial compositions of differentiated liquids (Table 3). The calculated liquids demonstrate strong enrichment in FeO (up to ~18 wt.%) and TiO2 (up to ~5.5 wt.%), consistent with the notion that the Skaergaard magma evolved in a manner typical of iron- and titanium-rich tholeiitic magmas [Brooks et al., 1991]. As Wager and Brown [1967] inferred from simple mass-balance considerations, there was essentially no silica depletion in the liquids from LZa through UZa. Phase equilibria calculations do, however, indicate a small increase in SiO 2 during formation of LZa. This agrees with the results of melting experiments for Ol - Pl assemblages in low-pressure tholeiitic systems [Grove and Baker, 1984]. The transition from the LZb ( Ol+Pl+Aug ) to LZc ( Ol+Pl+Aug + oxides) rocks is accompanied by a decrease in SiO2 as a result of continued crystallization of Ca-rich pyroxene, whereas the appearance of Mt and Ilm brings renewed silica enrichment.
It is interesting that this increase in SiO 2 is not as significant as it commonly is during crystallization of Fe-Ti oxides from tholeiitic magmas buffered for f O2 [Ariskin and Barmina, 1999, 2000]. It is certainly consistent with the absence or very small decrease in FeO (Table 3) that could be interpreted as evidence that the Skaergaard magma evolved as a system closed to oxygen [Osborn, 1959; Presnall, 1966; Toplis and Carroll, 1996]. Nevertheless, we draw attention to the fact that the decrease of f O2 within this temperature range is too sharp to be generated during simple closed-system crystallization. It moves us to conclude that the Skaergaard magma chamber has not been absolutely closed and could have been open to a reducing agent that was responsible for the change of oxygen fugacity during a middle-to-late stage of differentiation.
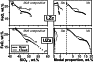
Another important factor bearing on the trend of differentiation is the modal proportions of primary mineral assemblages and residual (interstitial) liquids. Figure 10 summarizes the results of the geochemical thermometry calculations related to the original characteristics. The diagram to the right of the figure was constructed from average modal proportions calculated for each unit at the corresponding temperature (Table 3). The observed modal assemblages closely resemble the major calculated proportions of minerals for the main Skaergaard units. The only exception is probably over-estimated amounts of pigeonite in the UZa zone, although the mineral is known to present in small amounts there [McBirney, 1989; 1996]. Similarly, the modeled proportions of the evolving residual liquid through the LS section considered here was found to be about 50 wt.% (Figure 10). This may indicate that the compaction process was not efficient, at least at the early and middle stages of the Skaergaard magma differentiation. This conclusion is consistent with petrographic observations that adcumulus textures (expected to indicate a higher crystallinity) were widely observed at higher levels corresponding to UZb and UZc horizons [Wager and Brown, 1967]. Note, however, that the modal-proportion diagram in Figure 10 represents average values for the main units: in fact, the calculated amounts of intercumulus liquid differ for each particular rock, ranging from about 30% to 60% (as a residual porosity - Morse [1981]).
The most conspicuous contradiction of the results of geochemical thermometry is the obvious gap between LZa and LZb liquids and those of LZc through UZa (Table 3). It is seen in a small (~1 wt.%) return of CaO contents to higher and SiO 2 contents to lower values starting from the LZc liquid (Figures 11-13). The simplest explanation would be that the differences are due to uncertanties of the COMAGMAT program, because the gap is within the accuracy of the technique (compare the 1s deviations in Table 3). One could say that the COMAGMAT-3.65 model slightly under-estimates the crystallization temperature for Aug (Figure 5), so that later precipitation of the high-Ca pyroxene was modeled from more calcium rich liquids. Nevertheless, a nearly two-fold increase in TiO2 from LZb to LZc must also be explained because it would require at least 40 to 50% crystallization of the LZb melt. Thus, the observed gap may be an important genetic clue that should be examined more closely.
|
| Figure 14 |
First of all, note that Wager's classical trend is totally inconsistent with the standard low-pressure evolution of crystallizing tholeiitic magmas. With one exception, these points lie in the Ol - Pl field far from the experimentally defined Ol - Aug - Pl boundary, even though most of points should correspond to co-saturation with olivine and Ca-rich pyroxene. Only the last point is found to fall in the Ol - Pl - Aug - Pig field, but this is not surprising because the composition is similar to that of the Sandwich Horizon which is thought to represent an almost pure liquid that was the final product of differentiation [Wager and Brown, 1967]. It allows us to conclude that the trend of FeO versus SiO 2 calculated using inferred proportions of the main differentiated units of the Skaergaard intrusion (Figure 1) is actually artificial and does not provide a valid interpretation of all the major components of tholeiitic magmas. The only way it can be made to correspond to experimental data is to assume crystallization at elevated pressures where the CPX field is increased. In such a case, one should re-examine the previous pressure estimates of Lindsley et al. [1969] and assume that Aug crystallized as a primary mineral beginning from the LZa zone.
The experimentally determined compositions of McBirney and Naslund [1990] and the calculated compositions of residual liquids of Ariskin [1999]; this study] have a more realistic distribution in Figure 14. Most of the points are in the vicinity of the Ol - Aug boundary which spans a range of liquids in which the upper margin is shifted slightly towards CPX. This is consistent with the presence of augite as a primary liquidus mineral dominating the course of crystallization for the most of the Layered Series rocks. Note that the calculated TM, LZa, and LZb liquids are located very close to the curve with a trend directed straight towards the Pig field, whereas the LZc to UZa melts with more normative diopside are located above the Ol - Aug - Pig peritectic point. It is difficult to find a reasonable petrologic interpretation that can link the two slightly different series of residual liquids by simple crystal fractionation. The first one is most likely to reflect the early stages of differentiation along the normal trend of tholeiitic magmas as seen in volcanic suites [Ariskin et al., 1988; Hunter and Sparks, 1987; Toplis and Carroll, 1996]. The second trend may represent another type of chemical evolution that has only recently been suspected. Possible explanations include the possibility that the diopside normative and Ti-rich component was (i) a late stage residual liquid percolating upward through compacting crystals, (ii) an influx of the titanium and chlorine rich fluid at a middle-to-late stage [McBirney, in press], or (iii) some sort of compositional stratification in the main mass of magma. I think that any of the proposed mechanisms is linked with a more general Skaergaard problem concerning the absence of the mass-balance between probable parental magmas and the average Skaergaard intrusion composition.
If we assume the Skaergaard Layered Series was formed during a closed system process of crystal fractionation from a parental magma close in composition to the marginal gabbro or the calculated initial "trapped" melt (Table 1), one would expect the weighted average composition of the Layered Series and two Border Series to resemble that of the proposed parental magma. Because the original shape of the intrusion is unknown, it is very difficult to estimate reliable proportions between the LS, UBS, and MBS rocks. Nevertheless, there are reasons to consider the LS rock as constituting at least 40-50% of the intrusion rocks providing the main contribution to the whole-body composition [McBirney, pers. comm.].
The main feature of the Layered Series is the predominance
of magnetite- and ilmenite-rich
rocks that compose of about 70% of the observed section (Figure 10). These rocks contain
of 43 to 44 wt.% SiO
2, 5 to 6 wt.% TiO
2, and 22 to 23 wt.% FeO
 , so that the average
Layered Series composition must also be depleted in silica. The LS characteristics
used to
calculate a range of possible Skaergaard intrusion average compositions ( SIAC ), using varied
proportions of the UBS and MBS rocks. Some of the results for three different proportions
of
the LS, UBS, and MBS are listed in Table 5. For comparisons, two compositions representing
the chilled gabbro
KT -39 and our calculated initial "trapped" liquid (Table 1) are also included
into the table. Even a superficial view of the compositions reveals a strong misbalance
between
the parental compositions and that of the differentiated body. It is most apparent
for TiO2 and
P2O5 which are almost two fold higher in
SIAC as compared to the proposed parents.
Moreover, the intrusion composition has of 2-4 wt.% less SiO
2 and much more iron. The
observed discrepancy may be explained by the effects of closed- or open-system crystallization.
The "closed" interpretation includes two possibilities, one in which the bulk composition
of the
Layered Series has more SiO2 and less TiO2, FeO, and phosphorus than the exposed section.
This would imply a "Hidden Layered Series" with relatively silica-rich
Pl -
Opx rocks at depth
[Wager and Brown, 1967].
The second possible explanation postulates substantial amounts of
felsic differentiates almost completely removed by erosion
[Hunter and Sparks, 1987].
, so that the average
Layered Series composition must also be depleted in silica. The LS characteristics
used to
calculate a range of possible Skaergaard intrusion average compositions ( SIAC ), using varied
proportions of the UBS and MBS rocks. Some of the results for three different proportions
of
the LS, UBS, and MBS are listed in Table 5. For comparisons, two compositions representing
the chilled gabbro
KT -39 and our calculated initial "trapped" liquid (Table 1) are also included
into the table. Even a superficial view of the compositions reveals a strong misbalance
between
the parental compositions and that of the differentiated body. It is most apparent
for TiO2 and
P2O5 which are almost two fold higher in
SIAC as compared to the proposed parents.
Moreover, the intrusion composition has of 2-4 wt.% less SiO
2 and much more iron. The
observed discrepancy may be explained by the effects of closed- or open-system crystallization.
The "closed" interpretation includes two possibilities, one in which the bulk composition
of the
Layered Series has more SiO2 and less TiO2, FeO, and phosphorus than the exposed section.
This would imply a "Hidden Layered Series" with relatively silica-rich
Pl -
Opx rocks at depth
[Wager and Brown, 1967].
The second possible explanation postulates substantial amounts of
felsic differentiates almost completely removed by erosion
[Hunter and Sparks, 1987].
Results of our calculations indicate that the compositional difference between liquids "trapped" in marginal rocks ( TM ) and that of LZa is small (Tables 1 and 4, Figure 14). They are consistent with the observation that the composition of Pl at the base of the exposed Layered Series is similar to that in the uppermost part of the Upper Border Series (Figure 3). Thus, there are no reasons to assume a large volume of a "Hidden Layered Series", assuming, of course, that the initial Skaergaard magma was free of suspended crystals. If one suggests the Skaergaard magma came to the chamber with an amount of crystalline material ( Ol+Pl ) equilibrated with a liquid close to the TM composition [Ariskin, 1999], the existence of complementary troctolitic rocks is inevitable, despite of some geophysical data arguing against the huge Hidden Zone [Blank and Gettings, 1973; McBirney, 1975]. Even if some amount of hidden troctolitic material exists, however, it is unlikely that crystallization in a closed system could produce large volumes of rocks rich in Fe-Ti oxides without more felsic differentiates (see Figure 7 and Figures 11-13).
In recent years more attention has been given to open-system crystal fractionation in the Skaergaard magma chamber with a later influx of a fluid or melt that was very rich in iron and titanium. There is some evidence of this in the geological relations, trace-element distribution, and petrographic features [McBirney, 1995]. Thus, this alternative interpretation may be also attractive in the light of the calculated shift of the LZc to UZa residual liquids plotted in the OLIV - CPX - QTZ diagram (Figure 14). Note, however, that a postulated influx of iron-rich material is difficult to reconcile with the vast amounts of the fluid needed to alter the primary igneous rocks metasomatically, or with the recent geochemical evidences for differentiation under closed conditions [Jang and Naslund, 2001].
A specially calibrated version of the COMAGMAT program allowed
the author to define
the range of initial temperatures (1145 to 1085oC) and oxygen fugacities
(1-1.5
log units above
QFM to slightly below
QFM ) intrinsic to the original crystal mush from which the rocks from
LZa to UZa have been crystallized. In parallel, average major-element compositions
of residual
(interstitial) liquid were calculated for the same units (Table 3). The result demonstrates a
trend of continual enrichment of FeO
 (up to ~18 wt.%) and TiO
2 (up to ~5.5 wt.%) with only
minor variations in the SiO
2 contents (48 to 50 wt.%).
(up to ~18 wt.%) and TiO
2 (up to ~5.5 wt.%) with only
minor variations in the SiO
2 contents (48 to 50 wt.%).
Projection of the compositions onto the low-pressure OLIV - CPX - QTZ diagram (Figure 14) supports several lines of petrologic evidence that most of the Layered Series crystallized on an olivine-clinopyroxene cotectic (along with plagioclase and oxides). Wager's compositions, however, lie too far from the Ol - Aug boundary to represent a realistic approximation of the low-pressure Skaergaard magma evolution. The simple mass-balance approach that Wager [1960] proposed is not consistent with phase equilibria constraints.
Systematic differences observed between the calculated residual liquid compositions for LZa/LZb and LZc to UZa (which are unlikely to reflect fractional crystallization) are within the accuracy of the phase equilibria used in the model. If one examines the T - X diagrams in Figures 11-13, one is easily convinced that the liquid lines of descent at temperatures below 1100o C may be changed dramatically. For example, CaO contents in the calculated liquids may differ of 2 to 2.5 wt.% in a temperature range of 10oC. Nevertheless, we cannot exclude the possibility that the compositional differences discussed above could be the geochemical effects of a late-stage process involving migration and re-equilibration of interstitial liquids.
A remarkable feature of geochemical thermometry is its ability to estimate original modal proportions of the primary liquidus minerals and residual liquid. The results summarized in Figure 10 are in fairly good agreement with the observed mineralogical assemblages that define the main units of the Layered Series. Estimated amounts of interstitial melt range around 50 wt.%. I believe that estimate is correct for the rocks of LZa and LZb, but it may be underestimated by 10 to 20 wt.% for gabbros with abundant magnetite and ilmenite owing to a slightly over-estimated (up to 10oC) initial rock formation temperatures.
Finally, our interpretations of the results of phase equilibria modeling depend upon
the
accuracy of the COMAGMAT calculations. The problems we have outlined indicate that
even
careful calibrations giving a precision of
 10oC may be insufficient to give unambiguous
conclusions, especially when dealing with multi-phase assemblages
including 5-6 minerals plus
melt. This does not mean we are not confident of the utility of magma crystallization
models.
Despite the difficulties we have oulined, systematic phase equilibria modeling of
intrusive rocks
can be a controlling factor allowing petrologists to surmount the inadequacies of
other
techniques, such as mass-balance calculations. In the context of modeling the Skaergaard
rocks, the most serious need are experimental data on the melting relations of magnetite
and
ilmenite in assemblages spanning the unexplored range of Fe-Ti rich and silica depleted
compositions (Figure 4d). These data could be used in the future for more accurate
calibrations
of COMAGMAT and other magma crystallization models.
10oC may be insufficient to give unambiguous
conclusions, especially when dealing with multi-phase assemblages
including 5-6 minerals plus
melt. This does not mean we are not confident of the utility of magma crystallization
models.
Despite the difficulties we have oulined, systematic phase equilibria modeling of
intrusive rocks
can be a controlling factor allowing petrologists to surmount the inadequacies of
other
techniques, such as mass-balance calculations. In the context of modeling the Skaergaard
rocks, the most serious need are experimental data on the melting relations of magnetite
and
ilmenite in assemblages spanning the unexplored range of Fe-Ti rich and silica depleted
compositions (Figure 4d). These data could be used in the future for more accurate
calibrations
of COMAGMAT and other magma crystallization models.
This method is based on the premise that any crystal-liquid mush that produces a completely crystalline rock should pass through a stage when relative motions of solids and interstitial liquid have ceased, so that the system may be considered as closed. In this case, it is theoretically feasible to calculate all thermodynamic parameters for the initial system, using phase equilibria models designed for the calculation of equilibrium melting/crystallization relations in igneous rocks. Like the other methods, this approach entails certain assumptions as to the mechanisms of differentiation of intrusive rocks.
If crystals grew to sufficiently large sizes before settling to the floor, then the interstitial liquid would have approximately the same major- and trace-element concentrations as the liquid constituting the main part of convecting magma in which they were accumulated. This is also true if the crystals nucleated and grew in situ, with the residual liquid being exchanged by chemical diffusion with the main magma body. In both cases the average phase composition for the rock at any particular horizon may be given by the expression:
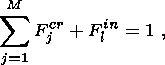 | (A.1) |
where
Fjcr and
Flin are initial modal proportions of
a particular mineral
j (1 j
j M ) and
interstitial liquid ( l ). The bulk chemical composition of such a crystal mush is expressed
as:
M ) and
interstitial liquid ( l ). The bulk chemical composition of such a crystal mush is expressed
as:
 | (A.2) |
where Cil(0) is the interstitial liquid composition, whereas Cij(0) should be attributed to average weighted contents of element i in mineral j accounting for a range of original compositions for each particular mineral.
The physical history of the formation of a rock from the crystal mush may be consistent with "closed" and "open" system evolution. The first situation means that cooling of the heterogeneous layer results in simple chilling (contact rocks), or interstitial crystallization with new minerals precipitated from the liquid matrix (orthocumulates). It is also possible that primary crystals undergo some amount of additional growth at the expense of the interstitial melt, followed by crystallization of the residual matrix. In all cases closed systems conserve the whole composition given by Equation (2), even though the compositions of individual primocrysts and interstitial material may change. The primary "trapped melt" temperature may be called by the formation temperature of the magmatic rock in the geochemical sense that the bulk rock composition did not change during further cooling. If so, Fjcr and Flin should be treated as initial or original modal proportions, with Cij(0) representing original mineral compositions [Ariskin and Barmina, 2000; Barmina et al., 1989a].
In "open" systems the original modal proportions may change by later growth or compaction of the crystals (increasing Fjcr ) and the accompanied exclusion of part of the initial interstitial liquid (decreasing Flin ). In addition, liquid percolation may give rise to a compositional re-equilibration of the initial primocrysts and migrating melts and significant modification of the initial bulk compositions, Cir. Nevertheless, in all of the open systems one can conceive of a stage when transport events cease. Beginning from this point, the percolating system is closed [Hunter, 1996], so that its whole chemistry defines the composition of the rock to be formed further in situ. It means that bulk modal and chemical compositions of the rocks produced during open system evolution can be also expressed by Equations (1, 2), but genetic interpretations of the values Fjcr, Flin, Cij(0), and Cil(0) must attribute them to one or more dynamic, probably late-stage, processes of reorganization.
If we assume the whole rock chemistry contains a record of the original rock formation parameters, there is the possibility of extracting such genetic information. Two main assumptions should be done to resolve the problem. The most important is that the liquid and crystals were in chemical equilibrium, with the formation temperature as an intensive parameter of the equilibrium. The second assumption is that there are samples having bulk compositions different from each other only due to variations of the modal proportions Fjcr and Flin, with the "trapped" liquid and temperature being the same.
If both assumptions are true, one can state that during equilibrium melting of samples having the same "formation temperature" the modeled liquid lines of descent will converge with falling temperature and intersect at a point in temperature-compositional space that represents the conditions under which the assemblage was formed [Frenkel et al., 1988a, 1988b]. Failure to find such an intersection would indicate the absence of the local thermodynamic equilibrium and a link between the values for Cij(0) and Cil(0). Thus, to decipher the genetic record of the rock it is necessary: (1) to select a group of samples for which one would expect the initial formation conditions to have been the same, (2) to conduct a series of physical or numeric equilibrium melting experiments for these samples, (3) to determine or calculate the chemical evolution of modeled liquids, (4) to construct T - X lines of this evolution for each sample and to identify the intersection point. In some aspects the approach is similar to the method of isotope geochronology in which an isochron is constructed by searching for an intersection point corresponding to the ages of the last isotopic equilibrium for both rocks and minerals [Ariskin and Barmina, 2000].
In practice, the method of geochemical thermometry is accomplished by means of the COMAGMAT phase equilibria model [Ariskin, 1999; Ariskin et al., 1993]. Although the program was primarily designed to simulate fractionation of basaltic magmas, it can also be used to calculate the course of equilibrium crystallization both for melts and cumulus rock compositions. Because equilibrium crystallization is reversible with respect to equilibrium melting, the construction of "melting" lines can be replaced with the crystallization trajectories for starting compositions identical to those of the rocks under consideration. Applying the method to natural assemblages, one should account for both analytical and computational uncertainties that yield formation temperatures with a determined error. As a rule, instead of an ideal intersection point (for a small number of modelled lines their convergence for each petrogenic oxide can be determined visually) one can see on the T - X diagrams a compact cluster of liquids lines of descent closing on one another in a range of 10-20o C that corresponds to the accuracy of the COMAGMAT model [Ariskin, 1999]. Our experience in the phase equilibria calculations for dolerites and diabases from differentiated sills [Barmina et al., 1989a, 1989b; Frenkel et al., 1989; Krivolutskaya et al., 2001], gabbros and troctolites from the Partridge River intrusion [Chalokwu et al., 1993, 1996] and large layered complexes [Ariskin et al., 2003; Barmina and Ariskin, 2002] has shown that the greater the contrast in compositions that are used, the more accurate the estimates of the trapped (interstitial) liquid temperature and composition that are obtained. This is confirmed by the results obtained for the rocks of the Skaergaard Marginal Border Series (Figure 2).
The results presented in this paper indicate that the determination of formation temperatures graphically, based on intersections of the modeled T - X trajectories (Figures 8-13), is somewhat subjective, because the approximate uncertainties of 10-15o C for this approach are close to the cited internal calibration accuracy of the COMAGMAT model. However, one must take into account the fact that the Layered Series rocks are differentiated. This imposes a set of important limitations on how one determines the original temperature and liquid composition for each sample: (1) the calcuated and observed "cumulus" mineral assemblage must correspond, (2) the modeled mineral compositions should be close (as much as possible) to those observed in selected rocks; and (3) melts entrapped in cumulates from higher levels of the Layered Series should represent lower temperature melts compared to those from underlying zones. Thus, the average values given in Table 4 were calculated for clusters of modeled T - X lines determined according to the petrologic restrictions given above. This does not allow one to specify strictly the accuracy of each calculated thermodynamic parameter, but provides an internally consistent approximation of T, log f O2, liquid component concentrations, mineral compositions, and original modal proportions.
The COMAGMAT programs rely upon mineral-melt equilibria geothermometers for olivine, plagioclase, augite, pigeonite, orthopyroxene, titaniferous magnetite, and ilmenite appropriate for a wide range of f O2 (from IW to NNO+1 buffers) and pressures from 1 atm to 10-15 kbar [Ariskin, 1999]. These semi-empirical dependencies were derived from a large dataset of experiments carried out mostly in tholeiitic systems covering compositions ranging from basalt to dacite. The general precision of phase equilibria calculations is about 10 to 15oC and 1 to 3 mol. % for each individual mineral. With such uncertainties, the use of mass-balance constraints in the COMAGMAT-3.5 model allows one to calculate equilibrium liquid compositions with an accuracy of 0.1 to 1 wt.%, which varies for different components and depends on the modal proportions between the melt and solids [Ariskin and Barmina, 1999, 2000].
A problem of application of COMAGMAT-3.5 to the Layered Series is the relatively low temperature mineral assemblages in LZc, MZ, and UZa rocks, ~1115-1080o C [McBirney, 1996]. In fact, the "silicate basis" of the COMAGMAT model was calibrated at higher temperatures of 1120-1350oC, with only a few points falling in the lower range. As a result, some calculations near 1100oC and below resulted in a shift of the modeled phase boundaries, e.g. producing an unrealistic enlargement of the Aug field at the expense of Pl and Pig. Moreover, calculated plagioclase compositions were found to be systematically more sodic and potassic than those observed in the natural assemblages. This forced me to reconsider and to modify the initial experimental dataset, drawing more attention to ferrobasaltic systems equilibrated in the vicinity of 1100oC.
To achieve this goal, we used the INFOREX experimental database
[Ariskin et al., 1996, 1997],
which now contains information from 290 melting experiment studies including over
10500 subliquidus runs. Searching the database for 1 atm experiments that resulted
in
saturation with
Pl, Ol, Aug, and
Pig oxides in the range 1050-1250o
C (run duration
oxides in the range 1050-1250o
C (run duration
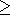 48 hours) yielded 270 experimental glass compositions
containing 7
48 hours) yielded 270 experimental glass compositions
containing 7
 FeO
FeO
 18 wt.%, 45
18 wt.%, 45
 SiO
2
SiO
2  60 wt.%,
and 2
60 wt.%,
and 2
 Na2 O+K
2 O
Na2 O+K
2 O
 5 wt.%. For most of the glasses (which are
classified as
ferrobasalts to ferrodacites - Figure 4), equilibrium mineral compositions have
been determined,
so that four subsets of 153 points for
Ol, 187 for
Pl, 125 for
Aug, and 43 for
Pig have been
formed. That mineral-melt information was processed in the manner of
Ariskin et al. [1993]
to develop a system of new mineral-melt geothermometers. The semi-empirical dependencies
have been incorporated into COMAGMAT and tested by solving the inverse temperature-compositional
problem, based on the initial dataset for each mineral. The new COMAGMAT
program (version 3.65) produced a small improvement in the temperature calculations
for
Pl,
Aug, and
Pig (as compared to COMAGMAT-3.5), although modeled plagioclase compositions
and phase relations between pyroxenes became more realistic. New olivine geothermometers
resulted in the temperatures and compositions similar to those obtained in the older
version and
were left unchanged. Thus, the new "ferrobasaltic" COMAGMAT-3.65 model was used for
phase equilibria calculations simulating equilibrium crystallization of the Skaergaard
rocks.
5 wt.%. For most of the glasses (which are
classified as
ferrobasalts to ferrodacites - Figure 4), equilibrium mineral compositions have
been determined,
so that four subsets of 153 points for
Ol, 187 for
Pl, 125 for
Aug, and 43 for
Pig have been
formed. That mineral-melt information was processed in the manner of
Ariskin et al. [1993]
to develop a system of new mineral-melt geothermometers. The semi-empirical dependencies
have been incorporated into COMAGMAT and tested by solving the inverse temperature-compositional
problem, based on the initial dataset for each mineral. The new COMAGMAT
program (version 3.65) produced a small improvement in the temperature calculations
for
Pl,
Aug, and
Pig (as compared to COMAGMAT-3.5), although modeled plagioclase compositions
and phase relations between pyroxenes became more realistic. New olivine geothermometers
resulted in the temperatures and compositions similar to those obtained in the older
version and
were left unchanged. Thus, the new "ferrobasaltic" COMAGMAT-3.65 model was used for
phase equilibria calculations simulating equilibrium crystallization of the Skaergaard
rocks.
Albarede, F., and A. Provost, Petrological and geochemical mass-balance equations: an algorithm for least square fitting and error analysis, Comput. Geosci., 3, 309-326, 1977.
Ariskin, A. A., Calculation of titanomagnetite stability on the liquidus of basalts and andesites with special reference to tholeiitic magma differentiation, Geochem. Intern., 36, (1), 15-23, 1998.
Ariskin, A. A., Phase equilibria modeling in igneous petrology: use of COMAGMAT model for simulating fractionation of ferro-basaltic magmas and the genesis of high-alumina basalt, J. Volcanol. Geotherm. Res., 90, 115-162, 1999.
Ariskin, A. A., and G. S. Barmina, An empirical model for the calculation of spinel-melt equilibrium in mafic igneous systems at atmospheric pressure: II, Fe-Ti oxides, Contrib. Mineral. Petrol., 134, 251-263, 1999.
Ariskin, A. A., and G. S. Barmina, Modeling phase equilibria at crystallization of basalt magmas (in Russian), 363 pp., Nauka/Nauka-Interperiodica, Moscow, 2000.
Ariskin, A. A., E. D. Konnikov, and E. V. Kislov, Modeling equilibrium crystallization for ultramafic rocks as applied to problems of the phase layering formation of the Dovyren pluton (Northern Baikal, Russia), Geochem. Intern., 2003 (in press).
Ariskin, A. A., G. S. Barmina, M. Ya. Frenkel, and A. A. Yaroshevsky, Simulating low-pressure tholeiite-magma fractional crystallization, Geochem. Intern., 25, (4), 21-37, 1988.
Ariskin, A. A., G. S. Barmina, S. S. Meshalkin, G. S. Nikolaev, and R. R. Almeev, INFOREX-3.0: A database on experimental phase equilibria in igneous rocks and synthetic systems, II, Data description and petrological applications, Comput. Geosci., 22, 1073-1082, 1996.
Ariskin, A. A., M. Ya. Frenkel, G. S. Barmina, and R. L. Nielsen, COMAGMAT: a Fortran program to model magma differentiation processes, Comput. Geosc., 19, 1155-1170, 1993.
Ariskin, A. A., S. S. Meshalkin, R. R. Almeev, G. S. Barmina, and G. S. Nikolaev, INFOREX information retrieval system: analysis and processing of experimental data on phase equilibria in igneous rocks, Petrology, 5, 28-36, 1997.
Barmina, G. S., and A. A. Ariskin, Estimation of chemical and phase characteristics for the initial magma of the Kiglapait troctolite intrusion, Labrador, Canada, Geochem. Intern., 40, (10), 972-983, 2002.
Barmina, G. S., A. A. Ariskin, E. V. Koptev-Dvornikov, and M. Ya. Frenkel, Estimates of the primary compositions of cumulate-minerals in differentiated traps, Geochem. Intern., 26, (3), 32-42, 1989a.
Barmina, G. S., A. A. Ariskin, and M. Ya. Frenkel, Petrochemical types and crystallization conditions of the Kronotsky Peninsula plagiodolerite (Eastern Kamchatka), Geochem. Intern., 26, (9), 24-37, 1989b.
Blank, H. R., and M. E. Gettings, Subsurface form and extent of the Skaergaard intrusion, East Greenland, Trans. Amer. Geophys. Union, 54, p. 507, 1973.
Brooks, C. K., and T. F. D. Nielsen, Early stages in the differentiation of the Skaergaard magma as revealed by a closely related suite of dike rocks, Lithos, 11, 1-14, 1978.
Brooks, C. K., and T. F. D. Nielsen, The differentiation of the Skaergaard intrusion, A discussian of Hunter and Sparks (Contrib Mineral Petrol 95: 451-461), Contrib. Mineral. Petrol., 104, 244-247, 1990.
Brooks, C. K., L. M. Larsen, and T. F. D. Nielsen, Importance of iron-rich tholeiitic magmas at divergent plate margins: a reappraisal, Geology, 19, 269-272, 1991.
Chalokwu, C. I., and N. K. Grant, Reequilibration of olivine with trapped liquid in the Duluth Complex, Minnesota, Geology, 15, 71-74, 1987.
Chalokwu, C. I., N. K. Grant, A. A. Ariskin, and G. S. Barmina, Simulation of primary phase relations and mineral compositions in the Partridge River intrusion, Duluth Complex, Minnesota: implications for the parent magma composition, Contrib. Mineral. Petrol., 114, 539-549, 1993.
Chalokwu, C. I., A. A. Ariskin, and E. V. Koptev-Dvornikov, Magma dynamics at the base of an evolving magma chamber: Incompatible element evidence from the Partridge River intrusion, Duluth Complex, Minnesota, USA, Geochim. Cosmochim. Acta, 60, 4997-5011, 1996.
Frenkel, M. Ya., A. A. Ariskin, G. S. Barmina, M. I. Korina, and E. V. Koptev-Dvornikov, Geochemical thermometry of magmatic rocks - principles and example, Geochem. Intern., 25, (6), 35-50, 1988a.
Frenkel, M. Ya., A. A. Yaroshevsky, A. A. Ariskin, G. S. Barmina, E. V. Koptev-Dvornikov, and B. S. Kireev, Dynamics of in situ differentiation of mafic magmas (in Russian), 216 pp., Nauka, Moscow, 1988b.
Frenkel, M. Ya., A. A. Yaroshevsky, A. A. Ariskin, G. S. Barmina, E. V. Koptev-Dvornikov, and B. S. Kireev, Convective-cumulative model simulating the formation process of stratified intrusions, in Magma-crust interactions and evolution, pp. 3-88, Theophrastus Publ. SA, Athens-Greece, 1989.
Frost, B. R., and D. H. Lindsley, Equilibria among Fe-Ti oxides, pyroxenes, olivine and quartz: Part II, Application, Amer. Miner., 77, 1004-1020, 1992.
Frost, B. R., D. H. Lindsley, and D. J. Anderson, Fe-Ti oxide-silicate equilibria: assemblages with fayalitic olivine, Amer. Miner., 73, 727-740, 1988.
Ghiorso, M. S., and I. S. E. Carmichael, Chemical mass transfer in magmatic processes II, Applications in equilibrium crystallization, fractionation and assimilation, Contrib. Mineral. Petrol., 90, 121-141, 1985.
Grove, T. L., Corrections to expressions for calculating mineral-components in "Origin of calc-alkaline series lavas at Medicine Lake volcano by fractionation, assimilation and mixing" and "Experimental petrology of normal MORB near the Kane Fracture Zone: 22o-25o N, mid-Atlantic ridge", Contrib. Mineral. Petrol., 114, 422-424, 1993.
Grove, T. L., and M. B. Baker, Phase equilibrium controls on the tholeiitic versus calc-alkaline differentiation trends, J. Geophys. Res., 89B, 3253-3274, 1984.
Henderson, P., The significance of the mesostasis of basic layered igneous rocks, J. Petrol., 11, 463-471, 1970.
Hoover, J. D., The chilled marginal gabbro and other contact rocks of the Skaergaard intrusion, J. Petrol., 30, 441-476, 1989.
Hunter, R. H., Texture development in cumulate rocks, in Layered intrusions, Elsevier Science B. V., Developments in Petrology, 15, 77-101, 1996.
4 Hunter, R. H., and R. S. J. Sparks, The differentiation of the Skaergaard intrusion, Contrib. Mineral. Petrol., 95, 451-461, 1987.
Hunter, R. H., and R. S. J. Sparks, The differentiation of the Skaergaard intrusion, Replies to A. R. McBirney and H. R. Naslund, to S. A. Morse, to C. K. Brooks and T. F. D. Nielsen, Contrib. Mineral. Petrol., 104, 248-254, 1990.
Jang, Y. D., and H. R. Naslund, Major and trace element composition of Skaergaard plagioclase; geochemical evidence for changes in magma dynamics during the final stage of crystallization of the Skaergaard intrusion, Contrib. Mineral. Petrol., 140, 441-457, 2001.
Kersting, A. B., R. J. Arculus, J. W. Delano, and D. Loureiro, Electrochemical measurements bearing on the oxidation state of the Skaergaard Layered Intrusion, Contrib. Mineral. Petrol., 102, 376-388, 1989.
Krivolutskaya, N. A., A. A. Ariskin, S. F. Sluzhenikin, and D. M. Turovtsev, Geochemical thermometry of the Talnakh intrusion: assessment of the melt composition and the crystallinity of the parental magma, Petrology, 9, 389-414, 2001.
Lindsley, D. H., G. M. Brown, and I. D. Muir, Conditions of the ferrowollastonite-ferrohedenbergite inversion in the Skaergaard intrusion, East Greenland, Miner. Soc. Amer. Spec. Publ., 2, 193-201, 1969.
McBirney, A. R., Differentiation of the Skaergaard intrusion, Nature, 253, 691-694, 1975.
McBirney, A. R., The Skaergaard Layered Series: I, Structure and average compositions, J. Petrol., 30, 363-397, 1989.
McBirney, A. R., Mechanism of differentiation in the Skaergaard intrusion, J. Geol. Soc. London, 152, 421-435, 1995.
McBirney, A. R., The Skaergaard Intrusion, in Layered intrusions, Elsevier Science B. V., Developments in Petrology, 15, 147-180, 1996.
McBirney, A. R., The Skaergaard Layered Series: Part V, Included trace elements, J. Petrol., 39, 255-276, 1998.
McBirney, A. R., and R. H. Hunter, The cumulate paradigm reconsidered, J. Geol., 103, 114-122, 1995.
McBirney, A. R., and Y. Nakamura, Immiscipibility in late-stage of the Skaergaard intrusion, Carnegie Inst. Wash. Yearb, 72, 348-352, 1973.
McBirney, A. R., and H. R. Naslund, The differentiation of the Skaergaard intrusion, A discussian of Hunter and Sparks (Contrib Mineral Petrol 95: 451-461), Contrib. Mineral. Petrol., 104, 235-240, 1990.
Morse, S. A., Kiglapait geochemistry IV: the major elements, Geochim. Cosmochim. Acta, 45, 461-479, 1981.
Morse, S. A., The differentiation of the Skaergaard intrusion, A discussian of Hunter and Sparks (Contrib Mineral Petrol 95: 451-461), Contrib. Mineral. Petrol., 104, 240-244, 1990.
Morse, S. A., D. H. Lindsley, and R. J. Williams, Concerning intensive parameters in the Skaergaard Intrusion, Amer. J. Sci., 280A, 159-170, 1980.
Nikolaev, G. S., A. A. Borisov, and A. A. Ariskin, New f O 2 -barometers for quenched glasses of various petrochemical series, Geochem. Intern., 34, (9), 753-756, 1996.
Osborn, E. F., Role of oxygen pressure in the crystallization and differentiation of basaltic magma, Amer. J. Sci., 257, 609-647, 1959.
Presnall, D. C., The join forsterite-diopside-iron oxide and its bearing on the crystallization of basaltic and ultramafic magmas, Amer. J. Sci., 264, 753-809, 1966.
Sack, R. O., I. S. E. Carmichael, M. Rivers, and M. S. Ghiorso, Ferric-ferrous equilibria in natural silicate liquids at 1 bar, Contrib. Mineral. Petrol., 75, 369-376, 1980.
Sato, M., and M. Valenza, Oxygen fugacities of the layered series of the Skaergaard intrusion, East Greenland, Amer. J. Sci., 280A, 134-158, 1980.
Snyder, D., I. S. E. Carmichael, and R. A. Wiebe, Experimental study of liquid evolution in a Fe-rich, layered mafic intrusion: constraints of the Fe-Ti oxide precipitation on the T-f O2 and T-c paths of tholeiitic magmas, Contrib. Mineral. Petrol., 113, 73-86, 1993.
Stormer J. C., Jr., The effects of recalculation on estimates of temperature and oxygen fugacity from analyses of multicomponent iron-titanium oxides, Amer. Miner., 68, 586-594, 1983.
Toplis, M. J., and M. R. Carroll, Differentiation of ferro-basaltic magmas under conditions open and closed to oxygen: implications for Skaergaard intrusion and other natural systems, J. Petrol., 37, 837-858, 1996.
Toplis, M. J., G. Libourel, and M. R. Carroll, The role of phosphorus in crystallization processes of basalt: an experimental study, Geochim. Cosmochim. Acta, 58, 797-810, 1994.
Tormey, D. R., T. L. Grove, and W. B. Bryan, Experimemtal petrology of normal MORB near the Kane Fracture Zone: 22o-25o N, mid-Atlantic ridge, Contrib. Mineral. Petrol., 96, 121-139, 1987.
Wager, L. R., The major element variation of the layered series of the Skaergaard intrusion and re-estimation of the average composition of the hidden layered series and of the successive residual magmas, J. Petrol., 1, 364-398, 1960.
Wager, L. R., and W. A. Deer, Geological investigations in East Greenland, Part III, The petrology of the Skaergaard intrusion, Kangerdlugssuaq, East Greenland, Meddelelser om Gronland, 105, 1-352, 1939.
Wager, L. R., and G. M. Brown, Layered Igneous Rocks, 558 p., Oliver and Boyd, Edinburgh, 1967.
Williams, R. J., Reaction constants in the system FeO-MgO-SiO 2 -O 2; intensive parameters in the Skaergaard intrusion, East Greenland, Amer. J. Sci., 271, 132-146, 1971.
Yang, H.-J., R. J. Kinzler, and T. L. Grove, Experiments and models of anhydrous, basaltic olivine-plagioclase-augite saturated melts from 0.001 to 10 kbar, Contrib. Mineral. Petrol., 124, 1-18, 1996.