V. S. Yakupov and S. V. Yakupov
Institute of Research in Space Physics and Aeronomy, Siberian Division of the Russian Academy of Sciences, Yakutsk, Russia
The geomagnetic field experiences both planetary and local time variations differing in periodicity and rate. Most difficult to study are slow variations of the field such as its westward drift, secular variations and decreases in its main (dipole) component. These difficulties are overcome by means of repeated magnetic surveys carried out over large time intervals. Generally they cannot resolve the detailed time-space structure of field variations that are still slow but faster than their types mentioned above. Of particular interest are comparatively slow variations of the geomagnetic field (more specifically, the magnetic flux through sufficiently large areas of the Earth's surface) in volcanic and rifting zones; such variations are related to the magma movement and thereby to the motion of the Curie point surface of magnetite (the most widespread ferromagnetic mineral in the crust). They can provide constraints on the state of dormant, active, extinct and embryonic volcanoes and are, in the long run, helpful for predicting volcanic eruptions and/or earthquakes. This prediction is particularly valuable because local variations in temperature and magnetic field intensity above a developing magma chamber undoubtedly antedate the related variation in the stress state of the overlying rocks giving rise to seismic events. The integral variations of the magnetic field above an active volcano and its vicinities are also interesting. Field variations in this case can be either fast or slow, due to the diversity of their origins: a change in the position of the Curie point surface under the volcano; volcanic ejection of a flow varying in density and velocity including rock fragments that carry remanent and inductive magnetization; flying rotating rocks fragments possessing a remanence (with an average magnetization possibly close to zero); possible presence of a deformable and moving magnetite Curie point surface in the ejecta cloud and fluctuations in the amount and distribution of the ejecta cooling below the Curie point above the volcano and in their magnetization if the material is heterogeneous; fall of magnetized volcanic products, fluctuations in the direction, velocity and density of their flux, and inhomogeneous spatial distribution of the latter; fluctuations in the flux velocity and density of ionized particles ejected by the volcano, ionization and recombination processes in the flux (in particular, outflow of ionized gases and cinder from the neck asymmetrical relative to the crater); lightning discharges in the ejecta cloud and other possible effects of electrification of particles during their detachment from a rock mass and due to mutual friction (prior to the shock wave resulting in the fracture of rocks with their possible ejection from the crater); electric discharges in a rock mass ("black lightning") increasing the electric field intensity to 10 7 V/m [Vorobyev, 1980]; enhancement of telluric currents due to changes in the electrical conductivity below and above the volcano; and so on. The study of processes activating the volcanic eruption and the eruption itself should be based on a combined approach using seismic, electrometric and magnetic methods and peripheral volcanic stations for assessing the space-time inhomogeneity of volcanic processes; filming for observation of airglow and evolution of the ejecta cloud; observation of space-time variations in the amplitude of the radar pulse reflected from various parts of this cloud and/or its attenuation in the cloud with the help of an aircraft with a high-precision positioning system; estimation of the temperature, electric charge and electric field intensity distribution in the cloud; and so on. However, all of the aforementioned phenomena are primarily due to the formation and development of the magma chamber; therefore, the observation of geomagnetic flux variations above the chamber is of primary importance.
Rapid variations in the magnetic flux through surface loops caused by lightning discharges and passage of meteorites were observed by Kalashnikov [1948], but these were relative measurements.
We propose an effective method for measuring the modulus of the magnetic flux through an arbitrary area of the Earth's surface. Let a closed loop with n coils of a preferably regular (but generally arbitrary) shape lie at a given time moment on a flat surface of the Earth (at moderate and high latitudes in both hemispheres where the vertical component contributes much to the geomagnetic field intensity). Then, the magnetic flux through the loop F is equal to nSB = nF0, where B is the average vertical component of the geomagnetic field induction within the loop of the area S, and F0 is the flux through one coil of the loop. We assume that the loop encompasses a volcano. Let the magnetic flux changes with time due to the varying magnetic induction and continuously changing (alternately decreasing and increasing) number of coils, with the loop remaining close. Then, an emf is induced in the multicoil closed contour of the loop:
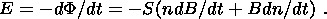 | (1) |
Since the rate of variation in the number of coils dn/dt can and must be maintained large and the magnetic induction variation rate dB/dt is either small or zero during the measurement period, the first (parenthesized) term in (1) can be neglected. Thus, the relation
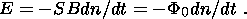 | (2) |
is valid with a reasonable (and controllable) accuracy. Hence, if the rate of variation in the number of coils is kept constant, the S value is known and E is measured, we find F0 = -E/Sdn/dt (the implementation of this idea has been developed by the authors and M. V. Yakupov). Monitoring of magnetic flux (and thereby field) variations using a single loop or a system of loops can be performed either continuously (e.g. in the case of active volcanoes) or in time intervals of the prescribed duration. In particular, monitoring of variations in the geomagnetic flux through volcanoes (regardless of the extent of their activity) must be conducted near large settlements or in densely populated areas (Vesuvius, the group of volcanoes near the town of Petropavlovsk-Kamchatski, and others). Among active volcanoes in Russia, of particular interest is apparently the Karymski Volcano in the Kamchatka Peninsula, whose activity has drastically increased in the last years (personal communication of S. A. Fedotov). A network of stations should be organized in active volcanic regions such as Iceland and Kamchatka for regular observations of geomagnetic flux variations. In areas where the Curie point surface occurs at depths not greater than ~2 km, its position can be determined using the technique of radar probing by magnetic field pulses [Yakupov and Yakupov, 2002]. Obviously, the method proposed for measuring the geomagnetic flux is equally applicable to its component produced by external sources of the magnetic field; their contribution can easily be eliminated because they operate over large areas and their monitoring is ensured by a network of observatories. In the equatorial region and adjacent areas where the horizontal component of the geomagnetic field prevails, the measuring loop should lie in the vertical or nearly vertical plane. For this purpose, it is possible to utilize natural and artificial relief forms striking E-W; narrow river valleys striking N-S, with upper parts of the loop fastened to bridges or special supports; and natural or artificial supports and structures, as well as relatively deep reservoirs including offshore areas.
In order to gain numerical estimates, we assume that the loop average
is 1 km
2, the average induction of the geomagnetic field is 0.5 Gs
(5
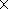 10
-5 A/m), and the alternating frequency is 100 Hz. Then,
according to (2) the induced emf is 5
10
-5 A/m), and the alternating frequency is 100 Hz. Then,
according to (2) the induced emf is 5
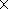 10
3 V if self-induction
is neglected. To estimate the possible effect of the self-induction,
we consider the differential equation determining the current strength
J in the closed part of the loop
[Tamm, 1956]
with the variable number of its
coils, resistivity
R = R0n and self-induction
L = L0n, where
R0 and
L0 are the resistivity and self-induction of one coil and
n is the number of coils in the circuit at a given time moment:
10
3 V if self-induction
is neglected. To estimate the possible effect of the self-induction,
we consider the differential equation determining the current strength
J in the closed part of the loop
[Tamm, 1956]
with the variable number of its
coils, resistivity
R = R0n and self-induction
L = L0n, where
R0 and
L0 are the resistivity and self-induction of one coil and
n is the number of coils in the circuit at a given time moment:
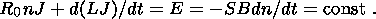 | (3) |
Let at any time moment the loop be a closed circuit with a number of coils n. We set
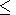 t
t 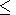 (n0 - 1)/v,
(n0 - 1)/v,
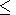 t
t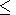 2 (n0
-1)/v.
2 (n0
-1)/v. We seek for a partial steady-state solution to (3) in the form J = E/R0n = J0/(1 + vt). Substituting it into (3), we obtain
This actually gives J = E/R0 (1 + vt) = J0/(1 + vt), and the self-induction emf values due to a change in the current strength and self-induction of the circuit cancel out and can be neglected. The complete solution of (3) should include, in addition to its partial solution, the general solution of the homogeneous equation
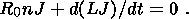 | (4) |
The solution
of (4) has the form
A exp(-B/t), where
A and
B are constants, and
therefore rapidly decreases with time, so that its contribution is
negligibly small in a steady-state regime. If
E can be reliably
measured starting from a value of 10 mV, a change in the vertical
component of the magnetic field
DZ can be determined starting from
10
-6 Oe (0.1
g ). We suppose that this change is due to
the
ascent of a magma chamber in the form of a vertical circular cylinder
with a radius
R. Let the Curie point surface be located at a depth
h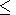 3R above the chamber. The vertical
component of the geomagnetic
field intensity above the center of the cylinder having a normal
magnetization
Jn is
-2pJn (1 - h/(R2
+ h2)1/2).
Taking logarithm of the increment
Dh = f(DZ/Z),
approximate calculations show that, given
h = 1 km,
the magnetic susceptibility
c = 10-4 and
Jn = cH = 10-6
3R above the chamber. The vertical
component of the geomagnetic
field intensity above the center of the cylinder having a normal
magnetization
Jn is
-2pJn (1 - h/(R2
+ h2)1/2).
Taking logarithm of the increment
Dh = f(DZ/Z),
approximate calculations show that, given
h = 1 km,
the magnetic susceptibility
c = 10-4 and
Jn = cH = 10-6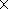 5
5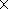 10-5,
a change of
Z by 0.1
g corresponds to a ~0.1-m shift of the
Curie point surface above the vertical cylinder modeling the magma
chamber. The actual value of this shift should apparently be
estimated at
10-5,
a change of
Z by 0.1
g corresponds to a ~0.1-m shift of the
Curie point surface above the vertical cylinder modeling the magma
chamber. The actual value of this shift should apparently be
estimated at
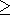 1 m, if one takes into account fast variations
and disturbances of the magnetic field, surface temperature
variations, difference between the real and model configurations
of the magma chamber, and so on.
1 m, if one takes into account fast variations
and disturbances of the magnetic field, surface temperature
variations, difference between the real and model configurations
of the magma chamber, and so on.
A method is proposed
for measuring the modulus (and its time variations) of the
geomagnetic flux through arbitrary areas of the Earth's surface.
Of particular interest are measurements of relatively slow flux
variations in active volcanic areas and rift zones, including
the monitoring of active volcanoes and assessment of processes
in dormant, extinct and embryonic volcanoes for predicting their
possible eruptions and associated seismic phenomena. Theoretical
estimates indicate that, if the magma chamber is modeled by a
vertical cylinder of radius
R, the detectable amount of the ascent
of the magnetite Curie point surface overlying the chamber at a
depth
h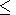 3R is ~0.1 m and more; the
real estimate should
apparently be raised to ~1 m.
3R is ~0.1 m and more; the
real estimate should
apparently be raised to ~1 m.
Kalashnikov, A. G., On a new method for studying weak variations in the geomagnetic field (in Russian), Izv. Akad. Nauk SSSR, Ser. Geogr. Geofiz., XII, (2), 137-146, 1948.
Tamm, I. E., Fundamentals of the Theory of Electricity (in Russian), GITTL, Moscow, 1956.
Vorobyev, A. A., Equilibrium and Energy Conversion in the Earth's Interiors (in Russian), Tomsk, 1980.
Yakupov, V. S., and S. V. Yakupov, Sounding of the Earth by magnetic field pulses (in Russian), Dokl. Ross. Akad. Nauk, 384, (6), 2002.