
A. V. Karakin
VNIIGeosystem, Moscow
Numerous studies [Fyfe et al., 1978; Grigoryev, 1971; Smith, 1968] provide evidence that the underground water forms a unified underground hydrosphere. Water (bound and free) in the crust is comparable in volume with ocean water and amounts to 4% of the crust volume. Such an amount of crustal water has a significant effect on all geological processes in the crust. One may naturally expect that the fluid effects are strongest in fractured, higher permeability layers, including waveguides. Therefore, the relevance of this problem is doubtless.

|
| Figure 1 |
Gutenberg [1959] supposed that seismic waveguides exist at asthenospheric depths. Afterward they were discovered in the upper mantle, lower crust and near the surface in rift zones. The low velocity zones were assumed to be related with the transition of the matter into amorphous state [Magnitsky, 1968] and with partial melting [Turcotte and Schubert, 1982]. This hypothesis suitable for the asthenosphere and consistent with its rheological properties was extended to the crust. However, temperatures in the crust (particularly in its upper part) are too low to account for the presence of melt inclusions throughout a large volume. Therefore, other hypotheses were also examined and majority of them related the waveguide properties to lithological distinctions of rocks (e.g. the presence of graphite-bearing rocks). The hypothesis on the lithological origin of waveguides encounters serious difficulties. One of the difficulties is the fact that the crust material is incessantly involved in upward and downward movements giving rise to folds and lithological unconformities, whereas waveguides occur, as a rule, horizontally at a fixed depth. This indicates that they are likely to be associated with the state, rather than composition, of the matter.
Comparison of seismic [Krasnopevtseva, 1978; Seismic Models..., 1980] and geoelectric [Vanyan, 1984; Vanyan and Shilovskii, 1983] data shows that low velocity and higher electrical conductivity zones often (but not always) coincide. The experimental data accumulated since the 1960s suggest that at depths not greater than 30 km these zones are most probably due to the presence in them of electrically conducting fluids [Vanyan, 1984]. The volume concentration of fluids in higher conductivity layers attains a few percent [Feldman, 1976; Vanyan and Shilovskii, 1983]. Furthermore, one cannot exclude a situation (most probable in the lower crust), when the fluid in the porous structure of waveguide is alternately represented by either melt or volatile (water) fluids, depending on the thermal regime.

|
| Figure 2 |
The picture is basically different in tectonically active regions, as is seen from Figures 2e, 2f. Figure 2e characterizes a 30-km thick continental crust under conditions of extension or shear (Basin and Range Province or San Andreas fault). The weakened brittle layer is at a depth of 10-15 km here. Given similar conditions and a crust stratified into granite and basite layers, two minimums appear at the bases of these layers (Figure 2f).
The weakened crustal zones fracture under strong shear deformations and develop into waveguides with fractured porous structure. This concludes the possible general description of the mechanism of waveguide formation. However, the generalized strength is too general and vague notion, and the actual fracture mechanism is more complex. Therefore, it is appropriate to consider other fracture schemes.

|
| Figure 3 |

|
| Figure 4 |
This concept implies that crustal waveguides are identified with the stick-slip faulting zone between the Forsch and Conrad boundaries. The dilatancy effect associated with the pore volume enlargement takes place in this zone. Also, listric faults widen and flatten out here as is evident from various geophysical observations. The dilatancy expansion gives rise to the vacuum effect of sucking a fluid [Nikolaevskii, 1990]. Note that this scheme is rather formal and very approximate. It does not account for changes in the direction and value of tectonic stresses, as well as effects of fluids and dynamics of layers. In particular, the scheme does not account for the fact that the structure of layers is largely dependent on their preceding state, implying that the structure and the properties of the crust are described by evolutionary geomechanical equations including state diagrams. Therefore, the Nikolaevskii scheme should be regarded as a starting hypothesis providing very general ideas.
The displacement of overlying layers along a waveguide can be effected through a mechanism similar to lubrication. This is consistent with the concept of tectonic stratification [Tectonic Stratification..., 1980] underlying the idea of two-stage plate tectonics [Lobkovskii, 1988]. In accordance with these schemes, the crust consists of layers strongly differing in viscosity. The upper, most rigid part of the crust is divided into microplates moving relative to one another similar to macroplates in the classical scheme of plate tectonics. The problem of driving tectonic forces responsible for the motion of the system as a whole is also solved within the framework of the latter. These forces produce intraplate deformations and displacements of upper layers relative to lower ones. The energy of global motion is converted into the energy of regional movements of microplates which can be intricate and involve several levels, because not only waveguides but also the lowermost layers of the crust, involved in the cataclastic flow, can be plastic.
The permeability of rocks (particularly in fault zones) is known to be rather high, and their strength is low in such zones. Therefore, on a geological time scale, fluids should have been inevitably expelled out of waveguides, cracks and pores would have been closed and the waveguides themselves would have disappeared. Simple estimates show that the lifetime of waveguides in the upper crust is on the order of 10 2 -10 4 years. There are no reasons to believe that waveguides exist only at present. Apparently, they have existed since the origination time of the continental crust. Then, a driving mechanism should exist which periodically sucks fluids back into the waveguide, thereby enhancing the fracturing of the latter.
The assumption on viscous rheology of some crustal layers is supported by geological and geophysical evidence and is consistent with the concept of the rheological [Nikolaevskii and Sharov, 1985] and tectonic [Peive, 1981] stratification, as well as with the concept of two-stage plate tectonics [Lobkovskii, 1988].

|
| Figure 5 |
The material of the lower layer can assume two states: dilatancy and compaction. The skeleton in the first state is elastic-brittle. The main factor controlling this regime is the Coulomb-Mohr law relating normal ( s ) and ultimate shear ( t ) stresses on a microlevel. When averaged and reduced to a macrolevel, this law is represented by certain relations connecting macroscopic quantities. Since the porous medium of waveguide is saturated, its stress state is defined by the Terzaghi principle, according to which the total stress tensor is divided into effective stresses sefij and pore pressure p:
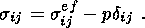 | (1.1) |
The Terzaghi principle states that the state of material is defined by the effective stress tensor, or more specifically, by its isotropic part. Another independent parameter of state is the porosity f. The higher the porosity, the more prone the porous structure skeleton to fracture.
The vertical force applied to the base of the elastic layer is constant in the thin-layer approximation; it is independent of the stress state of the two-layer system (in particular, it is independent of the dilatancy expansion in the lower layer) and is equal to the elementary column weight of the elastic layer. The deviatoric stresses at the waveguide depth being small compared to the rock pressure, the latter is constant at the waveguide top and changes with depth in accordance with the geostatic law. Only the pore pressure p and the isotropic component of the effective stress tensor sefkk experience significant variations. These quantities are interrelated via relation (1.1) and therefore the pore pressure may be taken as an independent controlling parameter p.
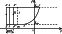
|
| Figure 6 |
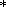 (f)
at which the skeleton structure
experience a qualitative change.
(f)
at which the skeleton structure
experience a qualitative change.
An elastoplastic dilatancy regime takes place at
pa < s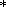 . It is
described by dilatancy equations which results from averaging
the formation process of cracks obeying each the Coulomb-Mohr
law. Due to shear loading under dilatancy mode conditions the
pore space expands, the pore pressure decreases, and the
waveguide sucks in fluids from both above and below. Faults
play the role of drainage channels. This process is known in
literature and has been repeatedly described as seismic (or
tectonic) injection or as a "seismic pump.'' The crack-pore
volume enlarges up to a maximum porosity value
f max at which
the porous structure skeleton fractures. The load is
transferred at this moment from skeleton to fluid, and the pore
pressure dramatically drops. At
pa > s
. It is
described by dilatancy equations which results from averaging
the formation process of cracks obeying each the Coulomb-Mohr
law. Due to shear loading under dilatancy mode conditions the
pore space expands, the pore pressure decreases, and the
waveguide sucks in fluids from both above and below. Faults
play the role of drainage channels. This process is known in
literature and has been repeatedly described as seismic (or
tectonic) injection or as a "seismic pump.'' The crack-pore
volume enlarges up to a maximum porosity value
f max at which
the porous structure skeleton fractures. The load is
transferred at this moment from skeleton to fluid, and the pore
pressure dramatically drops. At
pa > s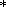 the pore pressure is so
high that the existence of a coherent skeleton is basically
impossible: the skeleton disintegrates into separate grains
that can move relative one another.
the pore pressure is so
high that the existence of a coherent skeleton is basically
impossible: the skeleton disintegrates into separate grains
that can move relative one another.
The waveguide material in this state is transformed into a porous-granular structure with a viscously deformable skeleton possessing both shear and bulk viscosities, and the deformation process is accompanied by fluid filtration. Such a medium is described by compaction (viscous consolidation) equations.
Drainage of the system in the compaction regime is very limited (because large cracks in outlet channels and faults are closed) and occurs through the low-permeability roof of the waveguide. Porosity in the compaction process decreases to its minimum value f = f min at which pores close. This is accompanied by resurrection of the skeleton from the nonviscous granular structure, the compaction regime is transformed into the elastic-plastic mode, and the cycle is further repeated.
I assume that the shear viscosity in compaction equations is constant and the bulk viscosity and hydraulic resistance (the inverse of permeability) are porosity dependent. Then, the compaction equations of motion are generally nonlinear. However, their solutions admit the principle of superposition of shear and volume deformations, i.e. these components of the solution can be treated independently of one another. Moreover, the volume deformations and filtration processes in the lower layer can be treated independently of the dynamics of the upper layer. The compaction phase duration is equal to the time required for pores to diminish under the action gravity from maximum to minimum sizes. This process determines the compaction phase time alone (and thereby the entire time interval of the wave motion) and does not affect the deformation mode of the two-layer system. The coupling of the upper and lower layers in the compaction phase affects shear deformations in the lower layer alone. Therefore, the elastic and viscous layers form a coherent system described by the Elsasser equation similar to the equation describing the two-layer asthenosphere-lithosphere system.
Thus, the pore space configuration changes at the maximum ( f max ) and minimum ( f min ) values of porosity. These states alternately change one another in a quasi-dynamic regime illustrated by the diagram in Figure 6. The cyclic structural variation is represented in this diagram by a closed contour. The single and double dashes indicate respectively the waveguide bottom and top in the dilatancy phase. The respective trajectory segments are vertical, because the pore pressure variation in the dilatancy phase are much weaker than in the compaction phase. The distance between these segments is DrgH1, where Dr the density contrast between the skeleton and fluid.
The entire system is set in motion by a horizontal force of tectonic origin applied to the upper elastic layer. This force supplies the energy to the entire process. To a first approximation, the upper layer is under the action of homogeneous horizontal normal stresses. The next approximation should account for tangential stresses and the gradient of normal stresses. The tangential stresses at the base of the elastic layer are in equilibrium with the normal forces in this layer and produce shear deformations in the lower layer. Thus, at any time moment the waveguide is under shear conditions.
The force of resistance of the lower layer to the upper one increases with the horizontal size of both layers and tends to infinity as the horizontal size infinitely increases. Accordingly, the normal tectonic force driving the system also tends to infinity. Nevertheless, the model equations admit a wave solution possessing periodical properties. Hence the necessity to separate periodic and aperiodic components of the solution and to correctly formulate the problem by specifying appropriate boundary and additional conditions.
Such a separation is based on the assumption that all nonstationary processes are periodic and the aperiodic component of the solution is stationary. The driving force of the process is represented by given stresses at infinity described by a static aperiodic component. These stresses and the work done by them are converted into a wave process. Consequently, these two components should be related through boundary conditions.
Note that the wave process complying with such an idealized formulation is unrealistic. In reality, a 3-D problem bounded in time and space should be solved. However, the possibility of a correct formulation of the problem and the existence of an idealized solution are basically important for understanding the physical nature of this process.
Upon separating a stationary, monotonically increasing component from the general solution of the two-layer system, a wave solution to the residual problem is sought for as follows. The dilatancy-mode porosity increases from its minimum to a maximum value. The compaction-mode porosity decreases from its maximum to the minimum value. The wave nature of the solution implies that the time t appears the wave argument x - ut, where u is the wave velocity found from the solution. Actually, the compaction equation alone includes the time derivative, so that the wave period is determined by the compaction phase duration. The wave solution can be considered existing if one succeeds in constructing a periodic solution for the wave argument. This process will be referred to as self-excited waves. Its driving force is provided by horizontal tectonic stresses. Due to the aforementioned specific properties of the waveguide material, the constant horizontal tectonic forces give rise to complex self-excited wave processes in the two-layer medium.
As mentioned above, the upper layer is described by equations
of the elasticity theory. Vertically uniform horizontal forces
directed along the positive direction of the
x axis are
applied at the lateral boundaries. The upper boundary is free
and tangential stresses resulting from the interaction with the
lower layer are applied at the lower boundary. I assume that
the wave moves in the negative direction of the
x axis. All
parameters of a stationary wave depend solely on the argument
y = x + vt. In the moving coordinate system, the definition
region
of length
L is bounded by the vertical boundaries
y1 < y < y3, L = y3 - y1
(Figure 5).
The lower and upper layers of thicknesses
H1 and
H2 are defined by the respective intervals
-H1
Here,
sij and
eij are the stress
and strain tensors,
q is the isotropic part of the strain tensor,
u is the displacement
vector, and
l and
m are the Lame coefficients reduced to the
plane case ( K = l + m
is the reduced bulk modulus). Thus, the
boundary problem for the upper layer reduces to the problem for
a weightless elastic layer with certain forces applied to its
boundary. Stresses vanish at the upper boundary of the layer,
whereas stresses and displacements
ui are continuous at its
lower boundary. The displacements vanish at the lower boundary
of the waveguide:
where the symbol
[sij]|+-
means a jump in the
quantity
sij at a given
boundary,
nj is the normal unit length vector.
The wave process implies certain periodicity conditions that
are authentically valid in the lower layer. In the upper layer
all quantities include both periodic and aperiodic components.
In other words, the horizontal stress
sxx and displacements
ux are represented as
Here,
E is the plane analog of the Young modulus, and
svxx
and
uvx are wave components of the horizontal
stresses and
displacements, which meet the periodicity condition
The values
s
However, one should keep in mind that in this case the values
sxx and
ux are no more than incremental stresses and displacements
measured from a certain mean level (which is, generally
speaking, infinite). By definition, we have
where
sxx and
ux are laterally averaged horizontal stresses and
displacements. The values
si and
ui are to be determined from the
solution. By definition the wave components meet the conditions
Averaging (2.4) over the vertical profile and taking (2.5) into
account yield additional relations for the average horizontal
stresses and displacements:
Stretching the vertical coordinate
z = ez
in 2-D elastic
equations (2.1), I obtain
Expanding the quantities in these equations into series
sij = s(0)ij
+ es(1)ij
+
Equations (2.7) imply that the horizontal displacement
u(0)x and
the normal stress
s(0)xx
are independent of the lateral coordinate
z: u(0)x
where
t is the tangential stress at the lower boundary.
Shearing forces are transmitted from the upper layer into
the
lower one, where they produce movements. Both possible states
characterized by the diagram in Figure 6 can be realized as two
phases: dilatancy (loosening the material) and compaction (or
viscous consolidation, decreasing the porosity). Equations of
motion and relevant boundary conditions are written out for
each of these phases. The resulting solutions are adjusted to
make them continuous at the boundary with the upper elastic
layer and at the phase interface. In particular, the continuity
condition imposed on the displacements and stresses at the
phase interface in the upper layer is
where
u2+ and
u2- are the
u values at the inner boundary when
approached from the right and from the left, respectively.
Substituting the second expression from (2.7) into the first
relation in (2.6) and taking (2.9) into account provide the
periodicity condition for the displacement increment (2.3).
Therefore, the first condition in (2.6) is not independent.
Expanding the second relation in (2.6) into a series, I obtain
Note that equation (2.10) contains the parameter
s
As shown above, the lower layer is always under the shear
conditions. Displacements in both dilatancy and compaction
phases are measured from the stationary component which is not
present in the constitutive equations of the phases. Both
deviatoric and isotropic components of stresses and strains are
assumed to be nonzero in both phases under shear loading
conditions. In this case their interrelation is essential and
includes the Coulomb condition and relationship between
increments in shear
gp
where
b is the dilatancy coefficient. The volume enlargement
phenomenon associated with shear was experimentally established
by Reynolds in 1885 and was called by him the dilatancy. The
tensor dilatancy equations consistent with the conditions of
Reynolds' experiment were formulated for the first time by
Nikolaevskii [1967, 1971].
Afterward similar equations and their partial cases were examined by
Rudnicki and Rice [Rice, 1980]
and other authors (Rudnicki and Rice studied the problem of
bifurcation in the solutions of these equations).
Following Rice [1980],
I introduce the plasticity moduli
mp, lp
and
Kp similar to elastic moduli. To simplify the plastic
strain case, I restrict myself to the shear strain
The plasticity moduli depend on the drainage conditions. I
assume that, in any dynamic processes, changes in the pore
volume are small compared to its average. Then, the dilatancy-phase
drainage conditions affect only the fluid regime in the
upper layer and have no effect on the plastic deformation mode
in the waveguide itself. This means that relation (3.1) includes
an undrained shear modulus at any (loading or unloading)
deformations. Another assumption is that the elastic strain
component is neglected. Then the total strain coincides with the
plastic component, and the dilatancy volume variation is only
controlled by the porosity variation
dq = df:
The third assumption is the consequence of the first two and
implies that the plasticity moduli
mp, lp
and
Kp are small compared to their elastic analogs
m, l and
K.
The physical meaning of these assumptions reduces to the statement
that the fractured medium in the lower layer is in a subcritical state.
This is the reason why the plasticity moduli and porosity variations are
small, and plastic shear strains are very large.
The fourth assumption relates to the structure of the layers. I
assume that the waveguide top is a low-permeability cap
ensuring the conditions of weak drainage of the waveguide. It
is due to this cap that, during a change in the state of the
medium, the weight of the upper elastic layer is transferred at
a critical point of the skeleton fracture from the skeleton to
fluid, as is required for the regime of viscous consolidation
in a medium with a fractured skeleton. If the cap mentioned
above is absent, the waveguide is unloaded under conditions of
elastic deformation. Such conditions are likely to exist in
crystalline shields such as the Canadian and Fennoscandian
shields. Ductile sedimentary rocks suitable for an impermeable
cap are absent there. Therefore, the oscillatory process in
such a waveguide does not include the compaction phase.
Substituting (3.1) into (3.2), I obtain
Let the strain in the lower layer be measured from the state
with a minimum porosity and a zero strain. The horizontal
displacement at the top of the waveguide
u is equal to the
horizontal, vertically uniform displacement of the elastic
upper layer. In each phase this horizontal displacement will be
measured from an initial point at which a given phase starts
developing. The initial point in the dilatancy phase is
y1 and the initial displacement is
u1. The respective values in
the compaction phase are
y2 and
u2. These values are evidently
connected through the kinematic relation
u - u1 = H1g,
which allows
easy integration of equations (3.2) and (3.3):
i.e. as shear strain increases in the waveguide zone, porosity
f and shear stress
t increase from their minimum values
f min and
t min
to critical levels
f max and
t max triggering the
fracture of the skeleton and the transition into the viscous
phase in accordance with the criterion illustrated in the
diagram of Figure 6
and based on the Terzaghi principle. If the
critical porosities
f min and
f max are known from the diagram
in Figure 6,
t min and
t max are values found
in the process of
solution. Equation (3.4) leads to the relation
relating
t max and
t min.
The aforesaid implies the validity of the following relations
at the boundaries between dilatancy and compaction zones:
The porosity
f = f max is the initial value of this parameter
in the compaction phase. The shear in the lower layer is
connected with the displacement of its upper boundary through
the relation
where
u2
Combining the second relation in (2.7), (2.8) and (3.4) yields
the equation
Solving (3.8) under condition (3.6) gives
Note that
a(y2 - y1)
These expressions give the boundary values
Relations (3.11) connect the dilatancy phase length with
amplitudes of stresses at the initial wave point.
According to [Karakin, 1990b, 1999],
the compaction equations admit the superposition principle, so that shear
and volume strain can be treated independently of one another. First I address
shear motions in the compaction zone that can be matched to
shear motions in the dilatancy zone. The calculations performed
for the elastic layer are all valid for the compaction zone.
However, they are different in the lower layer experiencing
viscous deformations. In particular, (3.3) is replaced by a
similar equation for viscous deformations:
Combining this equation with (2.8) and the second equation in
(2.7) yields the parabolic equation for a two-layer system
derived by Elsasser [1971]
The substitution of the wave argument in these two relations
yields the equations
The latter of these equations is readily solved with boundary
condition (3.6):
As expected, the tangential stress in the compaction zone
changes from its maximum to minimum values. Using (2.8), (4.1)
and (4.2), I obtain expressions for the normal stress and its
boundary value at the inner boundary:
Integrating (4.3a) and taking into account the periodicity
condition for displacements (2.12) yield
Displacement continuity condition (2.9) at the inner boundary,
with (4.4) and (3.7) taken into account, leads to the equation
Taking account of (3.10) and (4.3b), a similar relation follows
from the normal stress continuity condition (2.9):
Hence
v > 0, i.e. the wave (as expected) travels in the
direction opposite to the direction of the tectonic force
applied. Eliminating the indefinite values
t min and
t max in
(3.5), (4.5) and (4.6), I obtain the relation connecting the
lengths of the compaction and dilatancy phases
The periodicity condition for the normal stresses gives
The substitution of (4.4) and (3.10a) into (2.10) yields the
expression determining
u1:
Let
Tc be the time of compaction obtained below from the
solution of the boundary value problem of compaction. It is
connected with the wave velocity through the relation
which allows one to determine the compaction phase length ( y3 - y2).
The solution of equations (3.5), (4.5), (4.6), (4.8),
(4.9) and (4.10) determines the six sought-for quantities
u1, t min,
t max, (y2
- y1), (y3 - y2) and
v, expressed through
Tc.
This reduces the final solution of the problem to the determination of the
compaction time
Tc, which is found from the solution of the 1-D
compaction problem.
In this connection, I consider a 1-D compaction problem in the
finite region
-H1 < z1 < z < 0 with a moving boundary of the
trailing edge type described by the function
z1 = -H(x, t), where
H(x, t) is the thickness of the compaction layer. Following
[Karakin, 1999],
equations of 1-D low-porosity compaction have the form
where
S is the filtration flow,
f is porosity,
d is the
hydraulic resistance coefficient, and
z and
h are coefficients
of bulk and shear viscosity. The layer thickness is variable
and depends on the horizontal coordinate
x as a parameter. The
lower boundary of the viscous consolidation zone
G1 can be
either movable or fixed, depending on the viscosity value.
Various motion regimes are possible in the nonstationary case.
In particular, it is fixed at
f > f min and then the following
condition is valid at this boundary:
When the porosity at this boundary attains the value
f min, the
boundary starts to move upward until it encounters the upper
boundary
G2. The movement of the stationary wave
is only
consistent with the trailing edge condition at the lower
boundary:
The upper boundary of the waveguide
G2 is fixed. It is
overlain by a porous layer with an elastic skeleton. The
boundary value problem of elastic consolidation (the diffusion
equation) should be solved, and the resulting solution should
be joined to the solution in the waveguide. However, for the
purpose of qualitative analysis, the joining condition can be
replaced by a simpler constraint:
where
p
The initial time moment coincides with the onset time of the
compaction phase for each oscillation cycle. Because the
equations of shear and volume strain split into two groups, the
time enters each of these groups independently. The boundary
value problem (4.11)-(4.15) was numerically solved, and the
procedure and results of the solution are presented in
[Karakin and Levitan, 1993].
The time during which the length of the
compaction region decreases to zero is shown to be finite and
is the compaction period
Tc. This concludes the solution of
the problem.
Boundary condition (4.14) determines the across-waveguide
difference of pressure, which is greater than or on the order
of
DfK, where
Df is the total change of the porosity
over the
entire cycle of oscillation in the waveguide and
K is the
elastic bulk modulus of the upper layer. Since the dilatancy
bulk modulus
Kp is much smaller than
K, the pore pressure
varies in the dilatancy phase much weaker than in the
compaction phase. For this reason, the dilatancy phase
trajectories of the diagram in Figure 6 and phase interfaces are
vertical.
Thus, a self excited wave regime of motion can arise in a two-
layer system subjected to the action of a force. This regime is
related to periodic processes of fluid expulsion from and
suction into the waveguide layer. The compaction phase is much
longer than the phase of dilatancy expansion. The interaction
between these phases maintains the state of dynamic equilibrium
in the waveguide.
As is known, the theory of organic origin of oil encounters
basic difficulties. In terms of this theory, hydrocarbons
derive under suitable thermodynamic conditions from organic
matter uniformly dispersed throughout the sedimentary cover and
concentrate to form accumulations relatively small in volume.
This is a paradoxical fact. At first glance, it contradicts
thermodynamics, according to which all substances in the
dispersed phase tend to spread rather than concentrate. The
problem of resolving this paradox arises. This problem, albeit
in a less explicit form, also exists in the theory on inorganic
origin of oil. Similar to the first case, ascending
hydrocarbons of the endogenic origin should uniformly disperse
throughout the crust.
Another paradox is that advocates of both organic and inorganic
origin of hydrocarbons present equally convincing arguments in
favor of their hypotheses. Thus, both hypotheses seem equally
acceptable, and no unbiased criterion for the choice of them
exists.
These contradictions and paradoxes can be resolved if one
supposes that fluids in the crust are involved in oscillatory
movements and repeat many times their trajectories, both
vertically and horizontally. In this case the origin of
hydrocarbons is no longer the problem of basic importance and
is unrelated to the mechanism of their concentration.
The concept proposed explains many facts, in particular, the
position of mud volcanoes in rapidly subsiding basins at
anticlinal crests cut by faults. Fluid flows breaking through
anticlinal trap roofs can entrain hydrocarbons and mud-volcanic
breccia. They form mud volcano vents distinguished by weak
seismic contrast.
Hydrocarbon deposits of the Sakhalin shelf type can also
develop in terms of this model. As in the case of continental
deposits, traps cut by faults give rise to mud volcanoes rather
than hydrocarbon deposits (Figure 9). However, as distinct from
continental volcanoes, liquefied serpentinite rather than a
sand-clay mix is erupted in deep-sea trenches of subduction
zones.
Barcilon, V., and O. Lovera, Solitary waves in magma dynamics,
J. Fluid Mech., 204, 121-133, 1989.
Bott, M. N. P., The Interior of the Earth, Edward Arnold,
London, 1971.
Dmitrievski, A. N., I. E. Balanyuk,
Yu. A. Poveshchenko, A. V. Karakin,
and M. I. Lodzhevskaya, Mechanism for hydrocarbon
deposit emergence, Gas Industry of Russia, Digest, p. 5-9, 2000.
Elsasser, W. H., Two-layer model of upper mantle circulation, J. Geophys. Res.,
76, 1101-1112, 1971.
Feldman, I. S., On the nature of conductive layers in the
Earthºs crust and upper mantle, Geoelectr. Geotherm. Stud. KAPG Geophys. Monogr.
Bp., 721-745, 1976.
Fyfe, W. S., N. J. Price, and A. B. Thomson, Fluids in the Earth's
Crust, Elsevier, Amsterdam, 1978.
Gordin, V. A., and A. V. Karakin, Solitary wave solutions in
problems of viscous consolidation, Matem. Model., 2, (2),
98-116 (in Russian).
Grigoryev, S. M., The Role of Water in the Earth Crust Formation (Drainage Envelope
of the Crust), Nedra, Moscow,
1971 (in Russian).
Gutenberg, B., Physics of the Earth's Interiors, Academic
Press, New York, 1959.
Karakin, A. V., A model of the fluid motion in the crust over
geological time intervals, Mate. Model., 2, (3), 31-42,
1990a (in Russian).
Karakin, A. V., Crustal fluid dynamics models with an inelastic
skeleton, Izv. Akad. Nauk SSSR, Fiz. Zemli, (2), 3-15,
1990b (in Russian).
Karakin, A. V., General theory of compaction with a low
porosity, Fiz. Zemli, (12), 13-26, 1999 (in Russian).
Karakin, A. V., and L. I. Lobkovskii, Mechanics of a porous two-phase
asthenosphere, Izv. Akad. Nauk SSSR, Mekh. Zhidk. Gazov, (6), 53-63, 1979
(in Russian).
Karakin, A. V., and S. Yu. Levitan, Modeling of fluid dynamics
processes in rocks with a viscous skeleton, in Mathematical Modeling of Geological
Processes, p. 17-32, VNIIGeosystem,
Moscow, 1993 (in Russian).
Karakin, A. V., and G. N. Kambarova, A dynamic model of crustal
waveguides, Geoinformatika, (4), 10-17, 1997 (in Russian).
Krasnopevtseva, G. V., Geological and geophysical structural features of low-velocity
zones in the crust. An Overview: Regional, Exploration and Well Logging Geophysics,
VIEMS,
Moscow, 1978 (in Russian).
Lobkovskii, L. I., Geodynamics of Spreading and Subduction Zones and
Two-Stage Tectonics of Plates, Nauka, Moscow, 1988
(in Russian).
Magnitsky, V. A., Low-Velocity Zone in the Upper Mantle,
Nauka, Moscow, 1968 (in Russian).
McKenzie, D., The generation and compaction of partially molten
rock, J. Petrol., 25, 713-765, 1984.
Nikolaevskii, V. N., Relationship between volume and shear
plastic deformations and shock waves in soft soils, Dokl. Akad. Nauk SSSR, 177,
(3), 542-545, 1967 (in Russian).
Nikolaevskii, V. N., Constitutive equations of plastic
deformation in Loose Ground, Prikl. Matem. Mekh., 36,
1017-1029, 1971 (in Russian).
Nikolaevskii, V. N., Mechanics of Porous and Fractured Media,
World Scientific, Singapore, 1990.
Nikolaevskii, V. N., and V. I. Sharov, Faults and rheological
layering of the crust, Izv. Akad. Nauk SSSR, Fiz. Zemli,
(1), 16-27, 1985 (in Russian).
Overdeep Kola Drillhole, Nedra, Moscow, 1984 (in Russian).
Peive, A. V., Mobilism and tectonic stratification of the
lithosphere, Priroda, (2), 2-9, 1981 (in Russian).
Ranalli, G., and D. C. Murphy, Rheological stratification of the
lithosphere, Tectonophysics, 132, 281-295, 1987.
Rice, J. R., Mechanics of Earthquake Rupture, Amsterdam, 1980.
Seismic Models of the Lithosphere under Main Geological Structures of the USSR,
Nauka, Moscow, 1980 (in Russian).
Smith, F. G., Physical Geochemistry, Nedra, Moscow, 1968 (in
Russian).
Tectonic Stratification of the Lithosphere, Nauka, Moscow,
1980 (in Russian).
Turcotte, D. L., and G. Schubert, Geodynamics, Applications of Continuum Physics
to Geological Problems, Wiley, 1982.
Vanyan, L. L., Electrical conductivity of the crust in relation
to its fluid regime, in Crustal Anomalies of Electrical Conductivity, p. 27-34,
Nauka, Leningrad, 1984 (in Russian).
Vanyan, L. L., and P. P. Shilovskii, Deep Electrical Conductivity of Oceans and
Continents, Nauka, Moscow, 1983 (in
Russian).
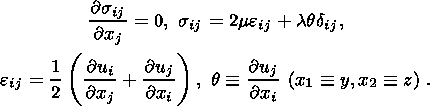
(2.1) 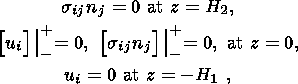
(2.2) 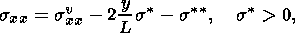
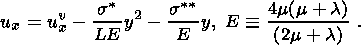
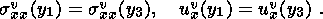
(2.3) 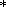 and
s
and
s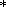
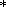 characterize forces applied at infinity,
which set the system in motion. More specifically,
s
characterize forces applied at infinity,
which set the system in motion. More specifically,
s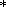 determines
the stress increase rate and
s
determines
the stress increase rate and
s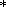
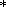 is related to the choice of the
reference point. The minus sign at these values indicates that
the forces are compressive. Strictly speaking, constant
s
is related to the choice of the
reference point. The minus sign at these values indicates that
the forces are compressive. Strictly speaking, constant
s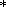
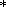 , as
well as stresses
sxx, tends to
infinity as the length of
layers increases. However, they can be subtracted from these
infinite stresses. In other words, the finite quantities
sxx = sxx
+ s
, as
well as stresses
sxx, tends to
infinity as the length of
layers increases. However, they can be subtracted from these
infinite stresses. In other words, the finite quantities
sxx = sxx
+ s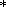
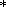 and
ux = ux + 2s
and
ux = ux + 2s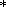
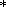 y/LE
are introduced instead of
sxx and
ux; below the previous notation of these values is
preserved (the tilde sign is omitted) because infinite stresses
and displacements are meaningless and are no longer used. As a
result, the boundary value problem considered in the interval
y1 < y < y3 includes solely finite stresses and displacements
which
can be represented as
y/LE
are introduced instead of
sxx and
ux; below the previous notation of these values is
preserved (the tilde sign is omitted) because infinite stresses
and displacements are meaningless and are no longer used. As a
result, the boundary value problem considered in the interval
y1 < y < y3 includes solely finite stresses and displacements
which
can be represented as
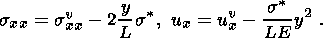
(2.4) 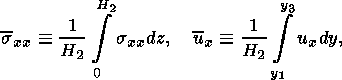
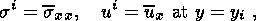
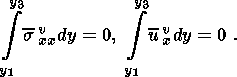
(2.5) 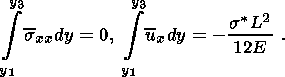
(2.6) 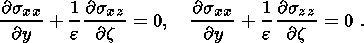
 etc., simple argumentation leads to the relations
etc., simple argumentation leads to the relations
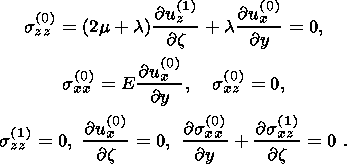
(2.7)  u(x) and
s(0)xx
u(x) and
s(0)xx s(x).
Integrating the last of equations (2.7) over the vertical profile and taking
into account boundary conditions (2.2) yield
s(x).
Integrating the last of equations (2.7) over the vertical profile and taking
into account boundary conditions (2.2) yield
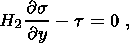
(2.8) 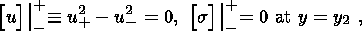
(2.9) 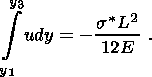
(2.10) 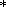 representing
the increase rate of static stresses at infinity. It is actually
a controlling parameter that describes the driving mechanism of
the system.
representing
the increase rate of static stresses at infinity. It is actually
a controlling parameter that describes the driving mechanism of
the system.
3. Dilatancy Phase
 epxz
and volume strain
qp:
epxz
and volume strain
qp:

(3.1) 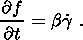
(3.2) 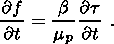
(3.3) 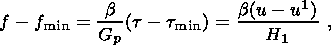
(3.4) 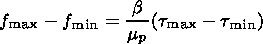
(3.5) 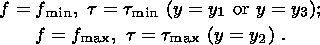
(3.6) 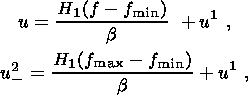
(3.7)  denotes values assumed by
u2 when the phase interface
is approached from the right and from the left, respectively.
denotes values assumed by
u2 when the phase interface
is approached from the right and from the left, respectively.
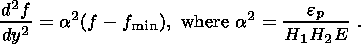
(3.8) 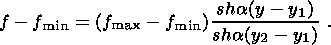
(3.9)  1. Since
E
1. Since
E mp,
the extent of the dilatancy
phase
y2-y1 is much greater than the layer thicknesses
H1 and
H2. Using (3.9), (3.7) and the second relation in (2.7),
expressions for displacement and stresses can be derived:
mp,
the extent of the dilatancy
phase
y2-y1 is much greater than the layer thicknesses
H1 and
H2. Using (3.9), (3.7) and the second relation in (2.7),
expressions for displacement and stresses can be derived:
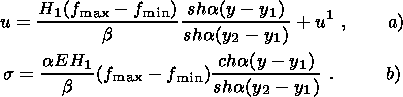
(3.10) 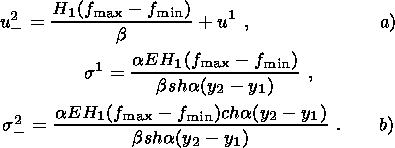
(3.11) 4. Compaction Phase

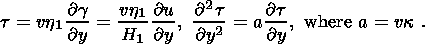
(4.1) 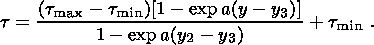
(4.2) 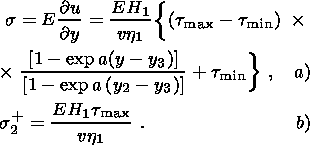
(4.3) 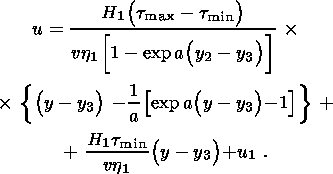
(4.4) 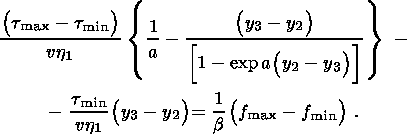
(4.5) 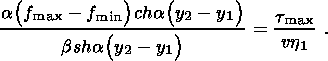
(4.6) 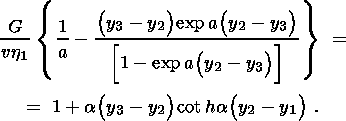
(4.7) 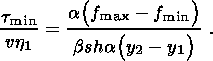
(4.8) 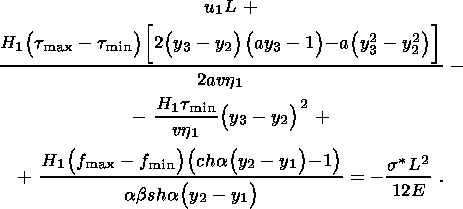
(4.9) 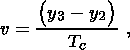
(4.10) 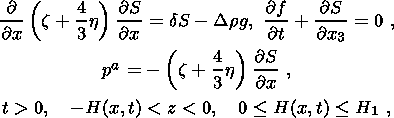
(4.11) 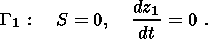
(4.12) 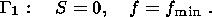
(4.13) 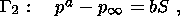
(4.14) 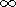 is the pore
pressure in the upper layer far from its
boundary ("at infinity''). This condition has the following
meaning. The characteristic time of the elastic consolidation
(estimated from the diffusion equation) is much shorter than
the viscous consolidation time. Consequently, this condition
does not contain the time derivative and is similar to the heat
transfer relation for the heat conduction equation. The
constant
b is expressed through geometrical and filtration
characteristics of the region with elastic skeleton overlying
the waveguide. The filtration flow direction changes its sign
at
p < p
is the pore
pressure in the upper layer far from its
boundary ("at infinity''). This condition has the following
meaning. The characteristic time of the elastic consolidation
(estimated from the diffusion equation) is much shorter than
the viscous consolidation time. Consequently, this condition
does not contain the time derivative and is similar to the heat
transfer relation for the heat conduction equation. The
constant
b is expressed through geometrical and filtration
characteristics of the region with elastic skeleton overlying
the waveguide. The filtration flow direction changes its sign
at
p < p and therefore
vanishes at this point. Then,
condition (4.14) provides qualitatively correct, albeit gross,
constraints on interaction of the two media at the boundary
G2. The system of boundary conditions
also includes the
initial condition for porosity. As mentioned above, this
condition is determined by the porosity at the dilatancy-to-compaction
transition moment and has therefore the form
and therefore
vanishes at this point. Then,
condition (4.14) provides qualitatively correct, albeit gross,
constraints on interaction of the two media at the boundary
G2. The system of boundary conditions
also includes the
initial condition for porosity. As mentioned above, this
condition is determined by the porosity at the dilatancy-to-compaction
transition moment and has therefore the form
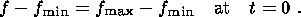
(4.15) 5. Conclusion: Vertical Migration of Fluids in the
Upper Crust
The functioning of the self-excited wave mechanism of the
fluid
motion in the waveguide and overlying layers is schematically
illustrated in Figure 7. In the dilatancy phase, downgoing fluid
flows entraining hydrocarbons In the dilatancy phase, downgoing
fluid flows entraining hydrocarbons enter the waveguide through
listric faults extending into it. The solubility of
hydrocarbons in water being very low (less than 1%),
they are
transported in the emulsion form in the upper crust where the
porosity in listric faults is rather high. Thermodynamic
conditions at waveguide depths are such that their solubility
(particularly, of their gaseous phase) increases. This is
beneficial to the accumulation and concentration of
hydrocarbons in the waveguide zone. Although the relative
amount of hydrocarbons transported over the individual wave
cycle is small, the amount of hydrocarbons entrapped in the
waveguide on the geological time scales and over large areas is
very large.

Figure 7
Fluids in the compaction phase are expelled upward from a
waveguide. Their motion can be obstructed by impermeable
anticlinal structures (traps), thereby developing abnormal
formation pressure. Traps are usually formed by anticlinal
folds of impermeable rocks. If ascending fluid flows strike
concentrated hydrocarbons, conditions for their accumulation
arise. If the crest of an anticlinal structure is cut by faults
(Figure 8),
fluids rush upward through the fault zones and are
ejected on the Earth surface, forming gas outbursts and mud
volcanoes. According to the hypothesis proposed in this work,
real oil and gas fields and mud volcanoes have a common origin.
The only distinction of mud volcanoes is that their traps are
fractured. This accounts for the fact that mud volcanoes
gravitate toward faults and shelf flexure zones, where
impermeable beds are most prone to fracturing.
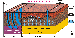
Figure 8
Using this concept, the motion of a two-phase gas-liquid mix
was numerically modeled for the upper crust of the Varandei-Adzvinskaya
oil-and-gas province
[Dmitrievski et al., 2000].
In particular, a numerical model was developed for the formation
process of gas fields in this region. A distinctive feature of
the geological structure and geodynamic development of this
region is the fact that it a former subduction zone that
developed as a result of the closure of an ancient ocean.
Huge
masses of sedimentary rocks were pulled into interiors in the
plate collision process at passive margins. These masses
contained large amounts of organic matter and are presently oil
source rocks, which have a large potential for the formation of
hydrocarbon deposits. However, its realization requires a
driving mechanism. Such a mechanism is represented by the self-excited
wave regime of motions in the crustal waveguide. Figure 9
schematically illustrates how the material of passive margins
is pulled down in a subduction zone at a passive margin.
Crustal waveguides that cross subducting lithospheric plates in
the horizontal direction form even during the subduction
process.

Figure 9
Some time after the subduction stops, an ex-collisional
structure similar to the Varandei-Adzvinskaya oil-and-gas
province develops in the former subduction zone (Figure 10). A
distinctive feature of subduction and particularly excursion-collision
zones is their typical across-strike differentiation
illustrated in Figure 10. Gas deposits are located in the frontal
part of the zone, corresponding to the sinking slab. Heavy oils
and bitumen occur in the back zone, and oils of intermediate
composition accumulate in the middle part of the zone. This
composition-type differentiation hydrocarbon deposits is
completely consistent with the driving mechanism of fluid
motion in the crustal waveguide. In the frontal part, fluids
enter the waveguide from below at high temperatures and
pressures. This is beneficial to the segregation of large
amounts of gas fraction from oil source rocks. In the back
part, oil source rocks overlying the waveguide are flushed at
low temperatures and pressures, which naturally leads to the
formation of heavy oils and bitumen.

Figure 10
References
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.1.3) on October 31, 2000.