M. K. Kaban
Schmidt United Institute of Physics of the Earth, Russian Academy of Sciences, (UIPE RAS), Moscow
 1o grid
within (30o-75oN, 14o W-195oE). Residual
mantle anomalies are calculated by
removing the anomalous model field from the observed gravity field. The mantle
anomalies are reliably separated into two components accounting for the effects
of different factors: (1) The regional component does not correlate, in a first
approximation, with crustal structures and reflects large-scale structural
heterogeneities of the Eurasia lithosphere, supposedly related to its thermal
regime. Intense positive anomalies characterize northern and central Eurasia,
and negative anomalies are observed in Western Europe and Southeast Asia. The
regional component is consistent with the shear wave velocity distribution
obtained from seismic tomography data. (2) The local component of the mantle
gravity field has wavelengths shorter than 2000-2500 km and evidently correlates
with specific tectonic structures. Maximum positive anomalies with amplitudes
exceeding 100 mGal characterize some structures of the East European platform
(Baltic Shield and Voronezh Massif) and East Siberia (Tunguska syneclise). A
chain of negative mantle anomalies is clearly traced west of the Tesseyre-Tornquist
line (Pannonian basin-Rhine graben-Massif Central). In Central Asia
the most prominent zone of negative mantle anomalies is located southwest of
Lake Baikal, approximately in the Khamar-Daban Range area. These anomalies are
likely to be related to intrusion of an anomalously hot and light mantle. The
intense negative mantle anomalies observed along the eastern boundary of Eurasia
are associated with backarc seas. A new map of the isostatic gravity anomalies
is calculated throughout the territory studied. As distinct from previous
studies, real data on the crustal structure, including variations in the
thickness and density of the sedimentary cover and solid crust, were used for
its calculation. The use of these data instead of the traditional Airy scheme
has led in many cases to a revision of notions concerning the isostatic state of
the crustal structures. In particular, as compared with previous maps,
significantly reduced amplitudes of the isostatic anomalies are obtained for the
South Caspian, Tien Shan and Urals regions.
1o grid
within (30o-75oN, 14o W-195oE). Residual
mantle anomalies are calculated by
removing the anomalous model field from the observed gravity field. The mantle
anomalies are reliably separated into two components accounting for the effects
of different factors: (1) The regional component does not correlate, in a first
approximation, with crustal structures and reflects large-scale structural
heterogeneities of the Eurasia lithosphere, supposedly related to its thermal
regime. Intense positive anomalies characterize northern and central Eurasia,
and negative anomalies are observed in Western Europe and Southeast Asia. The
regional component is consistent with the shear wave velocity distribution
obtained from seismic tomography data. (2) The local component of the mantle
gravity field has wavelengths shorter than 2000-2500 km and evidently correlates
with specific tectonic structures. Maximum positive anomalies with amplitudes
exceeding 100 mGal characterize some structures of the East European platform
(Baltic Shield and Voronezh Massif) and East Siberia (Tunguska syneclise). A
chain of negative mantle anomalies is clearly traced west of the Tesseyre-Tornquist
line (Pannonian basin-Rhine graben-Massif Central). In Central Asia
the most prominent zone of negative mantle anomalies is located southwest of
Lake Baikal, approximately in the Khamar-Daban Range area. These anomalies are
likely to be related to intrusion of an anomalously hot and light mantle. The
intense negative mantle anomalies observed along the eastern boundary of Eurasia
are associated with backarc seas. A new map of the isostatic gravity anomalies
is calculated throughout the territory studied. As distinct from previous
studies, real data on the crustal structure, including variations in the
thickness and density of the sedimentary cover and solid crust, were used for
its calculation. The use of these data instead of the traditional Airy scheme
has led in many cases to a revision of notions concerning the isostatic state of
the crustal structures. In particular, as compared with previous maps,
significantly reduced amplitudes of the isostatic anomalies are obtained for the
South Caspian, Tien Shan and Urals regions.
Density inhomogeneities in the upper mantle related to variations in temperature and mineral composition provide one of the main driving forces of both vertical and horizontal motions of lithospheric blocks. Information on these inhomogeneities can be gained from the gravity field. Unfortunately, the observed gravity field contains signatures of nearly all heterogeneities of the Earth. Therefore, in order to extract the mantle component, all mantle-unrelated effects should be eliminated from the observed field as effectively as possible; first of all, this is the crust effect because it is, on the one hand, the largest and, on the other hand, can be fairly reliably determined from a priori (mainly seismic) data independent of the gravity field. The residual gravity anomalies which can be called, within the accuracy (reliability) of the initial model of the crust, the mantle anomalies are most suitable for geodynamic reconstructions and for determining the patterns and intensities of processes responsible for the evolution of the mantle and lithosphere.
Attempts to calculate mantle gravity anomalies were made since the first deep seismic sounding (DSS) profiles were measured, but a reliable 3-D model could only be constructed after sufficient initial data on the crustal structure had been accumulated. The first gravity model of the lithosphere including a considerable part of North Eurasia was constructed by Artemjev et al. [1993, 1994a, 1994b], but the data used by these authors have been largely outdated by now. In particular, data from long DSS profiles (in total, a few ten thousand kilometers) are available now; they have provided unique constraints on the structure of the crust and upper mantle in vast areas of Siberia and East European platform [Egorkin, 1998; Kostyuchenko et al., 1999]. Moreover, Artemjev et al. [1993, 1994a, 1994b] did not conduct a comprehensive analysis of density inhomogeneities in the solid crust. Mantle anomalies in several regions of North Eurasia were calculated in a number of works. Yegorova and Starostenko [1999] analyzed a density model of the lithosphere under a part of the East European platform and Western Europe, but in some places (e.g. Baltic Shield) it is also based on outdated evidence on the crustal structure. A density model of the crust and upper mantle in southern regions of the former USSR was constructed in [Kaban et al., 1998]. It is important to note that results of regional studies cannot be directly compared because they usually employ different technologies including different reference models, relations between density and velocity, and so on. Therefore, the construction of a new map of mantle gravity anomalies throughout the territory of North Eurasia, using the newest data on the crustal structure and based on a consistent approach, is a relevant problem.
Tectonic processes significantly affect near-surface structures and the result is a concentration of density inhomogeneities appearing on the surface as topographic forms. Gravity anomalies (primarily local ones) contain information on hidden inhomogeneities of the sedimentary cover and basement and on a configuration of fault zones. Crustal faults have long been known to be mostly associated with zones of higher horizontal gradients of gravity anomalies. Many researchers emphasized that the isostatic reduction of gravity anomalies is most sensitive to fracture zones in which earthquakes can occur [e.g. Artemjev, 1975]. At that time, any isostatic gravity anomaly was considered as evidence for an isostatic disturbance of the crust. Subsequent studies showed that the isostatic gravity anomalies do not necessarily reflect deviations from isostasy; Grachev [1972] appear to have been first to note this fact. Isostatic models of that time were very simple, being usually represented by Airy schemes with a priori chosen parameters such as the normal crustal thickness at the sea level and the density jump at the crust-mantle interface. These models did not include density inhomogeneities within the crust and did not account for the variety of isostatic adjustment modes in various regions of the Earth. As a result, the inferred isostatic anomalies largely (as is clear now, predominantly) reflect, rather than deviations from isostasy, density variations in the upper part of the geological section, e.g. due to variations in thickness and density of sediments.
The development of isostatic studies during the last two decades has resulted in the revision and updating of many conventional conceptions. First of all, models used for calculating isostatic gravity anomalies have been much complicated. In their case study of the Tien Shan region, Artemyev and Golland [1983] were first to show that the use of an isostatic compensation model consistent with the actual crustal structure allows one to significantly reduce the isostatic anomalies as compared with the anomalies calculated in terms of the standard Airy scheme. Presently, detailed data on the structure of the sedimentary cover and its physical characteristics are available in many regions (e.g. see [Avchan and Ozerskaya, 1985; Bronguleev, 1986; Ermakov et al., 1989; Nevolin and Kovylin, 1993]); based on these data, many of the upper crust density inhomogeneities can be incorporated into the model. Additional constraints on the Moho depths (e.g. see [Hurtig et al., 1992; Kostyuchenko et al., 1999] have significantly improved isostatic compensation models. Recent studies showed that the use of updated models can significantly change the notions of isostasy in various regions [Artemjev and Kaban, 1986, 1991; Artemjev et al., 1994a, 1994b; Kaban, 1988], and this requires new calculation of isostatic gravity anomalies which can be regarded as a second main "geodynamic'' reduction of the gravity field.
Main principles underlying the method used in this work can be formulated as follows. At the first stage, an initial density model of the crust and upper mantle whose parameters are determined from the available a priori data is constructed. This model consists of two layers representing the sedimentary cover and solid crust, whose parameters are basically different. More detailed division is impossible for such a vast territory because the basement and Moho interfaces are the only reference boundaries that are consistently identified by nearly all seismic methods.
The sedimentary layer is usually inhomogeneous in both vertical and lateral directions. Moreover, density variations within the sedimentary cover often produce much larger gravity effect than variations in the depth to basement. This effect is most distinct in the cases when the thickness of the sedimentary cover exceeds 7-8 km because the density of sediments near its base is close to the density of their host crystalline rocks. Major sedimentary basins have been studied in detail using various geophysical exploration methods and reference drilling data. Therefore, a general density model of the sedimentary cover can be constructed in principle without interpreting the gravity field.
Drilling data reveal a very intricate structure of the sedimentary sequence including numerous local boundaries [Avchan and Ozerskaya, 1985]. Attempts to incorporate these boundaries into a general model (at least for one sedimentary basin) have usually been unsuccessful. The only approach suitable for a regional study consists in the use of general patterns of the density variations with depth and in their correction accounting for the lithology of a specific basin. Thus, each sedimentary basin or, if necessary, its part is specified by a concrete depth dependence of the density of sediments. Possible (and often fairly large) deviations from the general dependence are of local nature and are outside the scope of this study. Such an approach was successfully applied by several authors and proved effective [Artemyev et al., 1993; Kaban and Mooney, 2001; Yegorova and Starostenko, 1999]. In this work, the regional model of the sedimentary cover constructed in [Artemjev et al., 1993, 1994a, 1994b; Gordin and Kaban, 1995] is used.
In principle, the effect of solid crust density inhomogeneities can also be estimated from data on average velocities of seismic waves. However, the reliability of this information is lower than the reliability of other datasets including constraints on the Moho boundary position. Only the data on various types of waves measured on long DSS profiles (e.g., profiles measured by staff members of the GEON Center [Egorkin, 1991; Kostyuchenko et al., 1999]) yielded a determination uncertainty of the average velocity significantly smaller than its variations in the solid crust. Importantly, this uncertainty can be systematic and dependent on the interpretation method in use. Moreover, the velocity into density conversion introduces an additional uncertainty [Christensen and Mooney, 1995; Krasovskii, 1989]. In view of the above arguments, two models of the crust were used. The solid crust density in the first model was set constant. Accordingly, the residual anomalies obtained upon the removal of the crust effect from the observed gravity field account for density inhomogeneities in both the upper mantle and solid crust. The second model accounts for the density inhomogeneities of the solid crust derived from seismic velocities. Comparison of these results enhances the reliability of final conclusions.
The gravity field of the initial crust model is calculated relative to a horizontally homogeneous reference model. If the lower boundary of the model is also horizontal, the resulting field, will be independent, accurate to a constant, of the choice of the reference model. In order to exclude from the consideration the lower boundary until which the calculations are performed, the reference model should meet the following single condition: the density of its mantle should be equal to the average mantle density adopted in the initial calculations. In this study, a two-layer reference model with densities of 2.7 g/cm3 in the upper crust, 2.9 g/cm3 in the lower crust, and 3.35 g/cm3 in the mantle is used. The depth to the lower boundary is 34.3 km, coinciding with the average Moho depth within the region studied. The depth to the crustal density discontinuity (2.7/2.9 g/cm3 ) is 14 km, giving an average crust density of 2.84 g/cm3, which is consistent with worldwide data [Mooney et al., 1998].
At the second stage, additional density inhomogeneities are introduced in the upper mantle under the condition of a vanishing sum of all anomalous masses in each lithosphere column down to a specified level, including both the a priori known (topography, sedimentary cover and solid crust down to Moho) and additional mantle compensating masses. The field produced by additional density inhomogeneities in the upper mantle is subtracted from mantle gravity anomalies; the resulting isostatic gravity anomalies may be regarded as the second major characteristic of the geodynamic regime of a tectonic structure.

|
| Figure 1 |
 1o resolution.
The initial gravity field with
such a resolution was taken from the EGM96 model
[Lemoine et al., 1998].
For a significant part of Eurasia including the former USSR territory, the available
gravity data are more reliable and can be represented on a
10
1o resolution.
The initial gravity field with
such a resolution was taken from the EGM96 model
[Lemoine et al., 1998].
For a significant part of Eurasia including the former USSR territory, the available
gravity data are more reliable and can be represented on a
10
 15
15 grid,
which is
of major importance for isostatic anomalies because much information is lost due
to averaging. The initial field is represented by free-air anomalies with the
terrain correction applied within an area of a 200-km radius (the so-called Fay
anomalies).
grid,
which is
of major importance for isostatic anomalies because much information is lost due
to averaging. The initial field is represented by free-air anomalies with the
terrain correction applied within an area of a 200-km radius (the so-called Fay
anomalies).
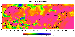
|
| Figure 2 |

|
| Figure 3 |
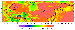
|
| Figure 4 |
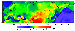
|
| Figure 5 |
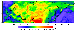
|
| Figure 6 |
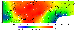
Significant information can be recovered from the analysis of the relationship between variations in the surface load (adjusted topography) and Moho depth. This relationship served as a basis for using the Airy model in early isostatic studies [e.g., Artemyev, 1975]. However, in the early 1980s it became clear that the parameters characterizing the relationship between the topography and Moho are generally not the same for different types of structures and their variations are related to density properties of the lithosphere (e.g. see [Artemyev and Golland, 1983]). The data presented here on the adjusted topography and crustal thickness variations provide a new basis for the analysis of this problem.

|
| Figure 7 |
|
| Figure 8 |

|
| Figure 9 |
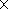 5o model
of Mooney et al. [1998].
Average velocity variations in the solid crust are fairly large and range from
6.3 to 7 km/s, which may indicate significant density variations.
5o model
of Mooney et al. [1998].
Average velocity variations in the solid crust are fairly large and range from
6.3 to 7 km/s, which may indicate significant density variations.
The problem of conversion of seismic velocities to densities does not have a unique solution [Christensen and Mooney, 1995; Krasovskii, 1989], although the relation between these parameters in solid crust rocks is more stable than in the sedimentary cover and upper mantle. In the present study, the velocity to density conversion relations derived by Christensen and Mooney [1995], allowing for possible differences in the rock composition (e.g. in oceanic and continental regions), are utilized. According to these authors, the possible uncertainty in the determination of density from P wave velocity on a regional scale (i.e. for relatively large structures) amounts to 0.05 g/cm3 for a separate layer and 0.03 g/cm3 for the solid crust as a whole. These values were used for estimating the reliability of results.
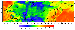
|
| Figure 10 |
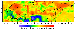
|
| Figure 11 |
|
| Figure 12 |
|
| Figure 13 |
|
| Figure 14 |
|
| Figure 15 |
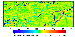
 300 mGal, considerably
exceeding their determination uncertainties that can attain 100 mGal in poorly
studied areas and range from 25 to 50 mGal in other regions, depending on the
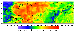
crustal thickness. The most prominent feature of the resulting field is its
distinct separation into the regional and local components shown in Figures 14 and
15. In a first approximation, the regional component does not correlate with the
crustal structure: vast areas characterized by anomalies of predominantly the
same sign include diverse structures. Intense positive anomalies with average
amplitudes of 100-150 mGal are observed in northern and central Eurasia. This
region is bounded in the west by the Tesseyre-Tornquist line, which is a
"geophysical'' (and "geological'') boundary between Western and Eastern Europe.
This line can be continued to the southeast where it divides the Greater and
Lesser Caucasus characterized by intense negative anomalies, although the
anomalous field here may have quite a different origin as compared with Western
Europe. To the east, the region of positive anomalies is bounded by a line
trending from the southwest, where it divides the Afghan-Tajik depression
overlying a very dense mantle and the Pamirs.
This line extends further to the
northeast along the northwestern boundary of the Sayany Mountains and Baikal
rift zone and reaches the Eurasia boundary near the Tiksi area. It is still
unclear to which megablock the Aldan Shield should be attributed. The
temperature field is likely to make the major contribution to the regional
variations in the upper mantle density, which is supported by results of the
surface wave interpretation
[Ekstrom and Dziewonski, 1998;
Ritzwoller and Levshin, 1998].
These authors discovered a high
S wave velocity zone that
extends to a depth of 250 km and exactly coincides with the above region of
mostly positive residual mantle anomalies. Heat flow data also support this
conclusion (a distinction between the thermal regimes of Western and Eastern
Europe has been rather reliably established
[Cermak, 1982;
Hurtig et al., 1992].
300 mGal, considerably
exceeding their determination uncertainties that can attain 100 mGal in poorly
studied areas and range from 25 to 50 mGal in other regions, depending on the
crustal thickness. The most prominent feature of the resulting field is its
distinct separation into the regional and local components shown in Figures 14 and
15. In a first approximation, the regional component does not correlate with the
crustal structure: vast areas characterized by anomalies of predominantly the
same sign include diverse structures. Intense positive anomalies with average
amplitudes of 100-150 mGal are observed in northern and central Eurasia. This
region is bounded in the west by the Tesseyre-Tornquist line, which is a
"geophysical'' (and "geological'') boundary between Western and Eastern Europe.
This line can be continued to the southeast where it divides the Greater and
Lesser Caucasus characterized by intense negative anomalies, although the
anomalous field here may have quite a different origin as compared with Western
Europe. To the east, the region of positive anomalies is bounded by a line
trending from the southwest, where it divides the Afghan-Tajik depression
overlying a very dense mantle and the Pamirs.
This line extends further to the
northeast along the northwestern boundary of the Sayany Mountains and Baikal
rift zone and reaches the Eurasia boundary near the Tiksi area. It is still
unclear to which megablock the Aldan Shield should be attributed. The
temperature field is likely to make the major contribution to the regional
variations in the upper mantle density, which is supported by results of the
surface wave interpretation
[Ekstrom and Dziewonski, 1998;
Ritzwoller and Levshin, 1998].
These authors discovered a high
S wave velocity zone that
extends to a depth of 250 km and exactly coincides with the above region of
mostly positive residual mantle anomalies. Heat flow data also support this
conclusion (a distinction between the thermal regimes of Western and Eastern
Europe has been rather reliably established
[Cermak, 1982;
Hurtig et al., 1992].
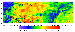
Unlike the regional field, the "local'' residual anomalies with wavelengths of less than 2000-2500 km clearly correlate with tectonic structures (Figure 15). Local variations of mantle anomalies in platform regions are much smaller than in tectonically active regions. Positive anomalies are most pronounced east of the Tesseyre-Tornquist line. For example, shields of the East European platform are characterized by intense positive residual mantle anomalies with amplitudes of up to +100 mGal. A similar anomaly is observed in the eastern Urals (Magnitogorsk zone). Mantle anomaly values above the Tunguska syneclise reach +100 mGal, which is consistent with the upper mantle P wave velocities that are also very high in this region [Deep Structure..., 1991; Egorkin, 1998]. A chain of negative mantle anomalies is clearly traced west of the Tesseyre-Tornquist line (Pannonian basin-Rhine graben-Massif Central).
At first glance, the inferred results do not confirm the hypothesis proposed by several authors, according to which the density of the upper mantle is significantly smaller under the Black and southern Caspian seas (e.g. see [Chekunov, 1979]). However, very deep basement subsidences and Moho uplifts within these structures compensate for each other so that the mantle anomalies are close to zero over the Black Sea and have a noticeable maximum over the Caspian Sea.
The intense negative mantle anomalies observed along the eastern boundary of North Eurasia are associated with backar marginal seas. The deepest parts of these seas are also characterized by the most pronounced anomalies. The thermal origin of these negative anomalies is evident.
Two well-resolved zones of negative residual mantle anomalies are recognized in Central Asia. One of them is located southwest of Lake Baikal, approximately in the Khamar-Daban area. Unfortunately, since this region is poorly studied by seismic methods, this anomaly cannot be localized more accurately. However, there is evidence indicating that this region and a somewhat less distinct region of negative anomalies near the northeastern part of the Baikal rift zone are related to mantle plumes [Grachev, 1998]. Another zone of intense negative mantle anomalies is located in the Karakorum and primarily Kun Lun Mountains areas approximately between the Tarim basin and Tibet. Additional evidences required to elucidate the origin of these anomalies are unfortunately unavailable.
Isostatic gravity anomalies are obtained as the difference between the observed gravity field and the field produced by an isostatically balanced lithosphere. In this study, the classical rigorous definition of isostasy is used, according to which the sum of anomalous masses in each lithospheric column above a certain depth, called the isostatic adjustment level, is zero. In addition to topography, anomalous masses of the sedimentary cover and Moho variations, density variations in the solid crust and upper mantle are introduced to obtain an isostatically balanced lithospheric column.
|
| Figure 16 |
|
| Figure 17 |
|
| Figure 18 |
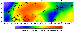
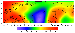
Local isostatic anomalies (Figure 16) mainly reflect the effects of three factors:
1. Isostatic disturbances due to the possible elastic support of the surface load and to the effect of mantle flows.
2. Density inhomogeneities in the sedimentary cover and basement that are not accounted for in the model.
3. Differences between the actual and model schemes of isostatic adjustment.
In this study, the effects of the second and third factors are considerably reduced (at least for large structures) due to the inclusion of the sedimentary cover density inhomogeneities and determination of an effective isostatic compensation model. Thus, the isostatic anomalies derived in this work ensure much better resolution of geodynamic pattern as compared with the previous studies.
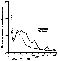
The intensity (variability) of the isostatic anomalies is directly related to the intensity of (present and past) tectonic activity in a specific region. The standard deviation of the field shown in Figure 16 is 10-16 mGal in platform regions, 18-20 mGal in regions where mountains formed long ago (e.g. the Urals), 36-57 mGal in areas with a high level of the recent tectonic activity (Alpine-Mediterranean foldbelt and Pamir-Altai, Tien Shan and Baikal regions) and reaches 70 mGal in the island arc and deep trench areas. Note that the incorporation of the actual structure of the crust has substantially reduced (by a factor of up to 2) the amplitudes of isostatic anomalies as compared with the model calculated according to the simplest Airy scheme and using solely topographic data [Artemyev, 1975]. A more detailed analysis of the isostatic anomalous field will be presented in the next part of this paper.

|
| Figure 19 |
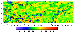
Gradient zones of the isostatic anomalies mostly delineate subvertical contacts of crustal rocks differing in density. Naturally, the majority of large faults should produce such contacts. In general, the lateral distribution of the zones supports this assumption. Furthermore, density contrasts across the faults in tectonically active regions should apparently be more expressed due to wider variety of rocks displaced by tectonic motions to different depths. Ancient deep faults in stable regions are buried under sediments and typically cut a basement surface strongly affected by denudation. Accordingly, the related gradient zones should be less intense. Thus, one may suppose that higher intensity fault zones are recognized in active regions, whereas stable regions include either ancient (dead) or passive fault zones. This conclusion is supported even by such example as the Urals Range: notwithstanding the widespread idea of very high gradients inherent in the field associated with contrasting density inhomogeneities in the Magnitogorsk zone, real gradients of isostatic anomalies there are significantly smaller than in tectonically active regions.
The above results lead to the conclusion that the gradient zones inferred in this work are authentic and reflect large fault zones (rather than the faults proper) which correspond to relatively extended deformation areas of the crust.
A density model of the North Eurasia crust is constructed and its gravity effect is calculated. The removal of this effect from the observed gravity field yielded residual mantle anomalies. They are reliably separated into two components reflecting the effects of the following factors.
1. The regional component does not correlate, in a first approximation, with the crustal structures and reflects large-scale structural features of the Eurasia lithosphere, supposedly related to its thermal regime. In particular, an intense positive anomaly is discovered in northern and central Eurasia, whereas negative anomalies are observed in Western Europe and Southeastern Asia. The regional component of the mantle gravity anomalies correlates well with the distribution of S wave velocities obtained by means of seismic tomography [Ekstrom and Dziewonski, 1998; Ritzwoller and Levshin, 1998].
2. As distinct from the regional component, the local component of the mantle anomalies with wavelengths shorter than 2000-2500 km clearly correlates with specific tectonic structures. The most pronounced positive anomalies with amplitudes exceeding 100 mGal characterize some structures of the East European platform (Baltic Shield and Voronezh Massif) and East Siberia (Tunguska syneclise). A chain of negative mantle anomalies is clearly traced west of the Tesseyre-Tornquist line (Hungarian basin-Rhine graben-Massif Central). The most prominent zone of negative mantle anomalies in Central Asia is located southwest of the Baikal rift zone, approximately in the Khamar-Daban area. These anomalies are likely to associated with intrusion of the anomalously light mantle. Intense negative mantle anomalies observed along the eastern boundary of Eurasia are related to backarc marginal seas.
A new map of the isostatic gravity anomalies is constructed throughout the territory studied. As distinct from previous studies, its calculation used real data on the crustal structure, including variations in the thickness and density of the sedimentary cover and solid crust. The use of these data instead of the traditional Airy scheme has led in many cases to a revision of notions concerning the isostatic state of crustal structures. In particular, the isostatic anomalies calculated for the South Caspian, Tien Shan and Urals regions are considerably reduced as compared with previous maps (e.g. see [Artemyev, 1975]). A joint analysis of the mantle and isostatic gravity anomalies intended to gain constraints on geodynamic settings of major tectonic structures in North Eurasia is a subject of the next stage of this study.
Artemyev, M. E., Isostasy in the Territory of the USSR, Nauka, Moscow, 1975 (in Russian).
Artemyev, M. E., and V. E. Golland, Isostatic compensation of Tien Shan; choice of compensation model, Phys. Solid Earth, 19, 30-37, 1983.
Artemjev, M. E., and M. K. Kaban, The free mantle surface - new possibilities to reveal subcrustal inhomogeneities from the structure of the Earth crust, J. Geodynam., 5, 25-44, 1986.
Artemjev, M. E., and M. K. Kaban, Isostatic processes and intracontinental orogenesis, J. Geodynam., 13, 77-86, 1991.
Artemjev, M. E., and M. K. Kaban, Density inhomogeneities, isostasy and flexural rigidity of the lithosphere in the Transcaspian region, Tectonophysics, 240, 281-297, 1994.
Artemjev, M. E., G. V. Demjanov, M. K. Kaban, and V. A. Kucherinenko, Gravity field of the lithosphere density inhomogeneities of Northern Eurasia, Phys. Solid Earth, (5), 12-22, 1993.
Artemjev, M. E., M. K. Kaban, V. A. Kucherinenko, et al., Subcrustal density inhomogeneities of the Northern Eurasia as derived from the gravity data and isostatic models of the lithosphere, Tectonophysics, 240, 248-280, 1994a.
Artemjev, M. E., V. M. Gordin, M. K. Kaban, et al., West Siberian Basin Basement Tectonic Segmentation. Final Report, Woods Hole Oceanographic Institution, USA and Inst. of Physics of the Earth, Moscow, Russia, 1994b.
Avchan, G. M. and M. L. Ozerskaya, Petrophysical Characteristic of the Sedimentary Cover in Oil and Gas Bearing Provinces of the USSR, Nedra, Moscow, 1985 (in Russian).
Belousov, V. V, and N. I. Pavlenkova, Structure of the Europe crust from seismic data, in Lithosphere of Central and Eastern Europe, edited by A. V. Chekunov, Naukova Dumka, Kiev, 1993 (in Russian).
Bronguleev, V. V., Ed., The 1:5,000,000 Map of the Pre-Riphean Basement Surface of the East European Platform, Mingeo SSSR, 1986 (in Russian).
Cermak, V., A geothermal model of the lithosphere and a map of the thickness of the lithosphere on the territory of the USSR, Phys. Solid Earth, 18, 18-27, 1982.
Chekunov, A. V., Ed., Gravity Model of the Crust and Upper Mantle, Naukova Dumka, Kiev, 1979 (in Russian).
Christensen, N. I., and W. D. Mooney, Seismic velocity structure and composition of the continental crust: A global view, J. Geophys. Res., 100B, 9761-9788, 1995.
Deep Structure of the USSR, Nauka, Moscow, 1991 (in Russian).
Egorkin, A. V., Structure of the crust from seismic geotraverse measurements, in Deep Structure of the USSR, p. 118-134, Nauka, Moscow, 1991 (in Russian).
Egorkin, A. V., Velocity structure, composition and discrimination of crustal provinces in the former Soviet Union, Tectonophysics, 298, (4), 395-404, 1998.
Ekstrom, G., and A. M. Dziewonski, The unique anisotropy of the Pacific upper mantle, Nature, 394, 168-172, 1998.
Ermakov, V. B., G. V. Krasnopevtseva, V. N. Semov, and Yu. K. Shchukin, Atlas of Maps Showing the Deep Structure of the Crust and Upper Mantle in the USSR, VNIIGeofizika, Moscow, 1989 (in Russian).
Feng, R., V. M. Gordin, M. K. Kaban, and Y. Wang, Gravity field and the mantle inhomogeneities in Central Asia, 30th Intern. Geological Congr. Abstracts, Beijing, vol. 1, p. 152, 1996.
Gize, P., and N. I. Pavlenkova, Structural maps of the Europe crust, Fiz. Zemli, (10), 3-14, 1988 (in Russian).
Gordin, V. M., and M. K. Kaban, Isostatic residual and decompensated gravity anomalies and gravity data on the upper crust heterogeneities (central and southern parts of the East-European platform and the Caucasus). Final report, Mobil Oil and Zonenshain Centre for Russian Geology and Tectonic, Univ. of Texas, Arlington, 1995.
Grachev, A. F., Gravity signatures of major neotectonic structural forms, in Geomorphology and Geophysics, edited by A. F. Grachev and L. Kulakov, p. 5-32, Nauka, Leningrad, 1972 (in Russian).
Grachev, A. F., The Khamar-Daban Ridge as a hotspot of the Baikal Rift from data of chemical geodynamics, Phys. Solid Earth, 34, 175-200, 1998.
Hurtig, E., V. Cermak, R. Haenel, and V. Zui, (eds.), Geothermal atlas of Europe, 1st ed., Hermann Haack Verlagsgesellschaft, 1992.
Kaban, M. K., Study of the Lithosphere Isostasy, Nauka, Moscow, 1988 (in Russian).
Kaban, M. K, M. E. Artemjev, A. I. Karaev, and A. P. Belov, The deep structure and geodynamics of the tectonic features in Turkmenistan and adjacent areas; gravity evidence, Geotectonics, 32, 323-332, 1998.
Kaban, M. K., and W. D. Mooney, Density structure of the lithosphere in the South-Western U.S. and its tectonic significance, J. Geophys. Res., 106, 721-740, 2001.
Kostyuchenko, S. L., A. V. Egorkin, and L. N. Solodilov, Structure and genetic mechanisms of the Precambrian rifts of the East-European Platform in Russia by integrated study of seismic, gravity, and magnetic data, Tectonophysics, 313, 9-28, 1999.
Kostyuchenko, S. L., L. N. Solodilov, and A. V. Egorkin, Characteristics of the structure and physical fields of the crust and upper mantle, in Neotectonics Geodynamics and Seismicity of Northern Eurasia, edited by A. F. Grachev, p. 291-308, Moscow, 2000.
Krasovskii, S. S., Gravity Modeling of the Crust with Implications for Isostasy, Naukova Dumka, Kiev, 1989 (in Russian).
Kusznir, N. J., The distribution of stress with depth in the lithosphere: thermo- rheological and geodynamic constraints, Phil. Trans. R. Soc. Lond., 337, 95-110, 1991.
Lemoine, F. G., N. K. Pavlis, S. C. Kenyon, et al., New high-resolution model developed for Earth's gravitational field, EOS Trans. Am. Geophys. Un., 79, 113-118, 1998.
Lithospheric Dynamics Atlas of China, China Cartographic Publishing House, Beijing, 1989.
Mooney, W. D., G. Laske, and T. G. Masters, CRUST 5.1: A global crustal
model at
5o 5o,
J. Geophys. Res., 103B, 727-747, 1998.
5o,
J. Geophys. Res., 103B, 727-747, 1998.
Nevolin, N. V., and Kovylin, Eds., Geological and Geophysical Modeling of Oil and Gas Bearing Provinces, Nedra, Moscow, 1993 (in Russian).
Ritzwoller, M. H., and A. L. Levshin, Eurasian surface wave tomography: Group velocities, J. Geophys. Res., 103, 4839-4878, 1998.
Volvovskii, I. S., and B. S. Volvovskii, Crustal Sections in the USSR from Deep Seismic Soundings, Sovetskoe Radio, Moscow, 1975 (in Russian).
Yegorkin, A. V., and A. V. Mikhaltsev, The results of seismic investigations along geotraverses, in Superdeep Continental Drilling and Deep Geophysical Sounding, edited by K. Fuchs, Ye. A. Kozlovsky, A. I. Krivtzov, and M. D. Zoback, p. 11-119, Springer-Verlag, Heidelberg, 1990.
Yegorova, T. P., and V. I. Starostenko, Large-scale three-dimensional gravity analysis of the lithosphere below the transition zone from Western Europe to the East European Platform, Tectonophysics, 314, 83-100, 1999.