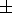 140 Ma by use of Sm-Nd method and as
2563
140 Ma by use of Sm-Nd method and as
2563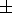 65 by use of Rb-Sr isotopes ratio
[Bernard-Griffiths et al., 1987].
65 by use of Rb-Sr isotopes ratio
[Bernard-Griffiths et al., 1987].
A. O. Gliko
Institute of Physics of the Earth, Academy of Sciences of Russia, Moscow, Russia
R. N. Singh and P. S. Swathi
Center for Mathematical Modeling and Computer Simulation, Bangalore, India
Origin of charnockites/granulites is one of the most fashionable and important problems in Earth's sciences. It has a key significance for understanding the nature of the lower continental crust and creates one of the most active fields of present day research. Really, the deep continental crust all over the world includes within it a close association of charnockitic granulites and metasediments of Archean - Proterozoic age. As a result of extensive uplift and erosion, parts of the former deep crust are exposed now in some places on old cratons (such as granulite terranes of Canadian, Baltic and Guyana shields). But only in the southern India and nowhere else a continuous cross-section through the middle to the lower crust is available for studying the processes operating over the full thickness of the continental crust. The practical importance of this problem is determined by the fact of close association of gold mineralization with fluid transport during formation of charnockites, and really, many gold-rich bearings are found in charnockitic terranes. Although there is a long history of studies and a large number of publication on this subject, including several outstanding monographs and reviews, the problem of origin of charnockitic rocks is still far from the solution and different points of view on their origin are discussed by petrologists. In our opinion, the verifying of these hypotheses based on the petrological and geochemical data could be done only by studying of physical aspects of charnockites formation (modelling of the thermal processes in the crust and mechanisms of fluid heat and mass transfer during the charnockitization). Here we make a first step in such a testing, based on the best and most comprehensive set of data available now only for the charnockites of the southern India and using the mathematical modelling as a main research instrument.
The charnockite assemblages include orthopyroxene, orthoclase (the characteristic mineral association for this type of rocks), clinopyroxene and some of the following minerals - plagioclase, hornblende, quartz, garnet, biotite and other accessory minerals such as ilmenite, magnetite, zircon. The chemical composition of charnockites can be represented by the following system of oxides: SiO2 -Al2 O3 -FeO-MgO-K2 O-Na2 O-Ti2 O-H2O.
Charnockite/granulite belt of the Southern India being one of the largest
granulitic provinces in the world occupies the extended parts of Karnataka,
Tamil-Nadu and Kerala, bounding from the south the gneisses and metasediments
of the oldest tectonic unit of the Indian shield - the Dharwar
craton. In accordance to the isotopic dating, most of the charnockites from
this region were formed in the late Archaen time 2500-2700 Ma. Only
charnockites of Kerala are interpreted to be younger and correspondingly
cover the time span 1930-540 Ma, according to U-Pd data
[Srikantappa et. al., 1985].
It is important that the age
determinations obtained by the use of different isotope methods
are very close. For instance, the age of charnockites from the area near
Chennai is determined as
2555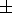 140 Ma by use of Sm-Nd method and as
2563
140 Ma by use of Sm-Nd method and as
2563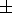 65 by use of Rb-Sr isotopes ratio
[Bernard-Griffiths et al., 1987].
65 by use of Rb-Sr isotopes ratio
[Bernard-Griffiths et al., 1987].
Pichamuthu [1954] was the first who proposed the formation of earlier group of charnockites by regional metamorphism of pre-existing Peninsular gneisses and Dharwar schists. Now the metamorphic nature of charnockites is widely recognised on the base of strong geochemical and petrological evidences. The particular significance has the fact of near identical chemical composition of charnockites and the old grey gneisses of the Dharwar craton [Ravindra Kumar et al., 1993]. The formations of the Dharwar and more broadly of almost all the Central cratonic region including gneisses, granites as well as large sequences of metasedimentary and metavolcanic rocks are metamorphosed in the greenschiest - lower amphibolite facies. The transitional zone between the craton and charnockite/granulite province is of 30-60 km wide and is characterised by the progressive increase of metamorphic grade approximately from the north to the south up to the granulite facies. This spectacular geological phenomenon provides a possibility to study "the arrested charnockites formation" - continuous transition from incipient to massive charnockites [Hansen et. al., 1987; Newton, 1988]. The mineral reactions leading to the formation of charnockites are these creating orthopyroxene and/or orthoclase (K-rich feldspar) instead of biotite, hornblende and quartz. The most important reaction creating both the characteristic minerals of charnockites - orthopyroxene and orthoclase and called the "charnockite reaction" is
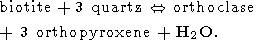 | (1) |
Other reactions which could be involved in the formation of charnockites are the following [Mueller and Saxena, 1977]
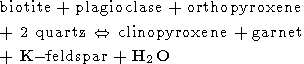 | (2) |
 | (3) |
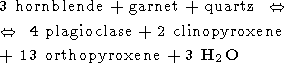 | (4) |
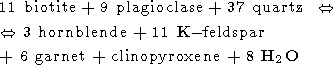 | (5) |
 | (6) |
From these five reactions the last one is the most important because it includes as the reactants only minerals certainly presented in the original rock of amphibolite grade (biotite, hornblende and quartz) and produces the minerals which are the most common in charnockites (two pyroxenes, K-feldspar and plagioclase). Reactions (2-4) include as the reactants such minerals as garnet and orthopyroxene. The parent gneisses contain low concentrations of garnet and do not contain orthopyroxen at all. So, these reactions can be considered only as auxiliary. The reaction (5) occurs at the P-T conditions of the upper amphibolite facies (T < 700oC) and has no direct relation to the charnockitization. The peak conditions of metamorphism estimated by use of different kind of geothermometers and geobarometers available for the granulite facies (see for review, for instance, [Mahabaleswar, 1993] are in the range of 700-800oC and 5-8 kbars, but in some places a pressure as high as 10 kbar (Nilgiri Hills) and temperature up to 850o C have been attained (Eastern Ghats). The main problem in the genesis of charnockites is related to very high temperatures attained during their formation. This temperature range is far beyond the melting temperatures of the appropriate silicate systems in the presence of water (600-650oC). The large amount of water certainly had to release during the charnockitization (we see from equation (1) that that formation of 1 mole of orthopyroxene is accompanied by the releasing of 1 mole of H2O) would led to the extensive melting and migmatization. However, any traces of such migmatization were found in rocks. Nor incipient charnockites of the transitional zone nor the massive charnockites are associated with migmatites. This fact is the most intriguing and its explanation is the key point of the "charnockite problem". Another problem concerns the thermal regime of the crust during the formation of charnockites - temperatures as high as 800o C were attained at the depth of 20-30 km (which correspond to the estimated pressures) inside a very broad region of lateral dimension of an order of thousand kilometres. So, if the first question which is addressed is:
The modern view on the first problem is based on the results of experimental studies of mineral reactions and processes of melting in the presence of fluid phase. It is well established that the increasing of the mole fraction of carbon dioxide in the H2 O-CO2 fluid suppress the activity of water, increases the melting temperature of silicate system under the given pressure and expands the stability field of the orthopyroxene-bearing assemblage being in equilibrium with the fluid into the higher temperatures [Philpotts, 1990]. This theoretical suggestion is supported by data on the composition of fluid inclusions in charnockites [Mohan et al., 1996; Santosh, 1988; Santosh et al., 1991; Srikantappa et al., 1992; Touret, 1988] which are very rich in CO2. It is remarkable that the CO2 - isochores for the high density inclusions yield a pressure and temperature range which is in accordance with the estimation from mineralogical thermobarometry. The dominantly carbonic composition of fluids during metamorphism of the charnockitic terranes is recognised now as a fact, although the origin of CO2 -rich fluid is under discussion. There are several comprehensive reviews of viewpoints on this subject and consequently on the origin of charnockites [Newton, 1988; Radhakrishna, 1993; Radhakrishna et al., 1990]. These views may be classified into the following four groups:
According to our estimate (see below), the minimal amount of CO2, required for the formation of charnockites, is approximately 4.98-3.88 wt % for a given metamorphic pile. Interaction of the sea water with andesitic or felsic rocks at the P-T range corresponding to the greenschist metamorphic facies (pressure up to 5 kbar and temperature T - 350-550oC) could lead to the formation of calcite. Decarbonation of 100 g calcite/aragonite (CaCO3 ) which would occur during the higher grade metamorphism at the later stage produces 44 g of CO 2 and 56 g of CaO. Thus, 2-4 wt % of CO2 could be produced from a pre-metamorphic pile containing 4.4-5.2 wt % of calcite. But the real content of calcite in gneisses, originated from the volcanic rocks of andesitic or felsic composition, does not exceed 0.5 wt % [Dobretzov, 1977], which corresponds to only 0.22 wt % of CO2. But even such a rate of sea water alteration is unreasonable to propose for a pile of parent gneisses as thick as 10-20 km.
So, the main conclusion came from the petrological studies is the mantle origin of the carbon dioxide involved in the formation of charnockitic rocks. Now we have a basis for the discussion of the required amount of CO2 and mechanisms of its transfer to the lower and middle crust.
We start from the main "charnockite reaction" (1)
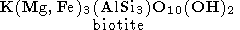 |
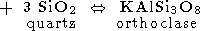 | (7) |
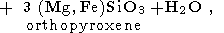 |
producing one mole of water and three mole of orthopyroxene instead of one mole of biotite and 3 mole of quartz. This relationship between mole fractions of orthopyroxene and water can be used for estimation of amount of water released during the formation of charnockite rock of a given composition if it could be argued that most of orthopyroxene has been appeared as a product of reaction (7). Because orthopyroxene could be formed also by reactions (3), (4) and (6), a retrospective analysis is required, and not in any case such an analysis could be done definitely. But upper limit for the amount of the released H2O can be easily estimated on the base of reaction (7), because it provides the highest mole fraction of water with respect to orthopyroxene - 1:3 as well as the reaction (6), when the other reactions give 1:4 and 1:5 (reaction (4) and (3), respectively). The composition of rocks from the St. Thomas Mount, Madras and of similar charnockites from Kerala probably is of the best choose for evaluating the amount of metamorphic water. These rocks contain from 5 to 10% of orthopyroxene as well as 2-15% of hornblende, 2-8% of clinopyroxene, 10-40% of plagioclase, but only a little of quartz and do not bear a primary biotite which is scarce and has the secondary origin [Srikantappa et al., 1985]. The practical absence of biotite and quartz indicates the genetic relationship to the reaction (7). In this case the estimated upper bound for the amount of water released during the high-grade metamorphism would be very close to its real value. From the equation (7) we see that this reaction produces 18 g of water per 332 g of orthopyroxene. Thus, for the metamorphosed rock containing 5-10% of orthopyroxene, the amount of water released in the process of dehydration of parent gneisses would be in the range 0.27-0.54 wt %.
Now we are able to evaluate the minimum amount of CO2 required for the formation of charnockites by use the available data on the composition of CO2-H2O fluid phase during metamorphism. In accordance with estimates of Touret et al. [1997], the mole fraction of H2 O in the metamorphic fluid have must be lower than 0.3:
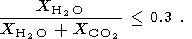 | (8) |
It follows from here that the required amount of CO2 (in wt % with respect to the bulk of the rock) can be evaluated as m = 7.32 p, where p is the amount of water released during the dehydration reaction. It gives m = 1.98-3.88 wt %. So, finally we obtain the following limits for the minimum amount of CO2 - 0.99-1.94 wt %, for the charnockite containing consequently, 5 and 10% of orthopyroxene. This is a minimal amount providing the required decrease of the activity of water, but the larger amounts are not precluded.
The recognising of the mantle origin of CO2 -rich fluid involved in
the formation of granulites (and in particular charnockites) poses a question
of the form in which the carbon dioxide could be stored in the mantle and the
problem of its transport to the lower and middle crustal level. The data
of experimental petrology show that carbonates such as dolomite and magnesite
would be stable phases at the deep mantle conditions although would rarely
survive transport to crustal levels
[Canil, 1990;
Eggler, 1976].
Such a survival requires extremely high rates of decompression and
sufficiently coarse original aggregates
[Ganguly et al., 1995;
Ionov et al., 1993].
Thermal disturbances in the mantle associated with the convective instabilities
and formation of plumes led to the decomposition of carbonates and creation
of carbonate-rich magmas, which under rapid uprising give rise to the
nephelenitic volcanism and under some special conditions to carbonatitic
lavas flow
[Le Bas, 1977].
But retaining in equilibrium with mantle, they can react, crystallise and
release CO2 vapour at pressures 25-27 kbar, which corresponds
to the
depth ~70 km
[Lee and Wyllie, 1998;
Wyllie and Huang, 1976].
Some evidences for such a process have been obtained from the
study of kimberlites
[see Jones and Wyllie, 1985].
There are reasons to propose much more intensive generation and transport of
carbonated melts in the Precambrian resulting in the formation of large
kimberlitic bodies in the lower lithosphere as it was argued by P. Wyllie.
Another indirect evidence comes from the fact that most of the large alkaline
complexes are of Proterozoic age. From the other hand, the role and scale of
volcanic processes comparing to the igneous activity at the
crustal levels was certainly much higher in the Archean time than during the
subsequent periods. Beginning from this point we should discriminate two
possibilities of carbon dioxide transfer through the lithosphere in the
Archean time - first is the transport of CO2 in the form of a separate
fluid phase (probably mixture of CO2 and H2O with predominance
of CO2 ), and the second - transport of CO2 by uprising nephelinitic
or alcaline basaltic magmas partly in the form of solution
and partly in the form of inclusions (the solubility of CO2 in silicate
melts decreases strongly with decreasing of pressure and becomes practically
zero at P 15 kbar).
15 kbar).
The first variant could be viewed a priory as a buoyancy driven flow in
the rigid, elastic or viscous matrix, depending on the rheology of the
lithosphere.
Ganguly et al. [1995]
assumed the rock matrix to be rigid and carbon dioxide to be transported in
accordance with the D'Arcy theory of filtration. They were able to derive an
analytical solution for that model and study quantitatively
the possible role of CO2 as an agent heating the middle crust up to
temperatures corresponding to the conditions of granulite facies. They showed
that the flux of CO2 required for rising of temperature up to 800oC would
be no less than 112.5-180 mol/m2 year under condition
that such
a high flux values are sustained during the period of no less than,
correspondingly 35 and 10 Ma. They compared these flux values with the
available estimates of the present carbon dioxide outflow
from the mantle and in the Archean time with the conclusion that 0.01-2%
of the total CO2 outgassed during the Archean had to be focused through
southern India. No attempts have been made on the way to consider the transport
of carbon dioxide in the framework of models with elastic or viscous rock
matrix although the appropriate mathematical methods are successively used
in the modelling of volcanic gases emanation induced by the inflation of
magma chamber and also in the study of melts transport in the mantle and
metamorphic fluids in the crust (we refer here only to some publications -
[Bonafede, 1990;
Khodakovskii et al., 1998;
McKenzie, 1984;
Natale el al., 1998;
Spiegelman, 1993a;
Wiggins and Spiegelman, 1995].
The models of this kind are free from the difficulties which are related to
the variants of magma underplating and give a simple
explanation for the observed strong heating of the crust and at the same time
the lack of intrusions in the most of the charnockite province of the South
India. But the total amount of carbon dioxide required for the rise of
temperature up to the granulite facies range, estimated by
Ganguly et al. [1995]
as 18
year under condition
that such
a high flux values are sustained during the period of no less than,
correspondingly 35 and 10 Ma. They compared these flux values with the
available estimates of the present carbon dioxide outflow
from the mantle and in the Archean time with the conclusion that 0.01-2%
of the total CO2 outgassed during the Archean had to be focused through
southern India. No attempts have been made on the way to consider the transport
of carbon dioxide in the framework of models with elastic or viscous rock
matrix although the appropriate mathematical methods are successively used
in the modelling of volcanic gases emanation induced by the inflation of
magma chamber and also in the study of melts transport in the mantle and
metamorphic fluids in the crust (we refer here only to some publications -
[Bonafede, 1990;
Khodakovskii et al., 1998;
McKenzie, 1984;
Natale el al., 1998;
Spiegelman, 1993a;
Wiggins and Spiegelman, 1995].
The models of this kind are free from the difficulties which are related to
the variants of magma underplating and give a simple
explanation for the observed strong heating of the crust and at the same time
the lack of intrusions in the most of the charnockite province of the South
India. But the total amount of carbon dioxide required for the rise of
temperature up to the granulite facies range, estimated by
Ganguly et al. [1995]
as 18 1018 kg
or 4
1018 kg
or 4 1020 mol for the
territory occupied by the south Indian
granulites seems to be too high. But the main difficulty of this model comes
from the assuming the rigid matrix. Because the driving force for the flows is
the buoyancy related to the density difference between
the rocks and the carbon dioxide, the pressure in the rock matrix and in the
fluid CO2 phase would be different. The application of the model
with the
rigid rock matrix is restricted by the requirement
that the stresses arising in the matrix are small comparing to the strength of
the rocks and the deformations of the matrix are also small enough. But in the
case of carbon dioxide transport from the depth of 70 km the pressure difference
in the rock matrix and in the fluid phase could be higher
than the real strength of rocks. This difference in pressure
DP can
be estimated as
DP = Dpg(h2-h1),
where
Dp is the
mean density difference between the rock and CO2, and
h1 and
h2 correspond to the crustal level and to the depth
from which carbon dioxide
start to move as a separate phase. For
Dp
1020 mol for the
territory occupied by the south Indian
granulites seems to be too high. But the main difficulty of this model comes
from the assuming the rigid matrix. Because the driving force for the flows is
the buoyancy related to the density difference between
the rocks and the carbon dioxide, the pressure in the rock matrix and in the
fluid CO2 phase would be different. The application of the model
with the
rigid rock matrix is restricted by the requirement
that the stresses arising in the matrix are small comparing to the strength of
the rocks and the deformations of the matrix are also small enough. But in the
case of carbon dioxide transport from the depth of 70 km the pressure difference
in the rock matrix and in the fluid phase could be higher
than the real strength of rocks. This difference in pressure
DP can
be estimated as
DP = Dpg(h2-h1),
where
Dp is the
mean density difference between the rock and CO2, and
h1 and
h2 correspond to the crustal level and to the depth
from which carbon dioxide
start to move as a separate phase. For
Dp  2000 kg/m
3,
h1 = 20 km and
h2 = 70 km, we get
DP
2000 kg/m
3,
h1 = 20 km and
h2 = 70 km, we get
DP 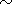 10 kbar.
It means
that the model assuming the transport of CO
2 as a separate phase should take
into account the rheology of the rock matrix.
10 kbar.
It means
that the model assuming the transport of CO
2 as a separate phase should take
into account the rheology of the rock matrix.
The second variant was proposed by several authors, but only on the way of purely qualitative speculation [Harris et al., 1982; Hopgood and Bowes, 1990]. This scenario is attractive as it provides a simple and natural explanation for the thermal event, but could be not so easy in explaining the lacking of volcanic products contemporary with the charnockites. Another question arises when we look at the possible traces of the magma underplating in the structure of the crust - mantle interface which could be revealed by geophysical methods. The teleseismic tomography infers the relatively low velocity in the crust and upper mantle which is in contrast to the general expectations for higher seismic velocities for the models with underplated layer of basic magma. This is a question of great interest, and we shall discuss it in the end of this paper.
There are numerous publications concerning the study-state thermal models of the continental crust and especially of the old Precambrian shields [Jessop and Lewis, 1978; Mareschal and West, 1980; Singh and Negi., 1980; West and Mareschal, 1979]. These very simple models predict the temperature distribution in the stable continental crust due to the heat generation in the uppermost felsic crustal layer highly enriched in radiogenic elements and heat flow supplied to the base of the crust from the mantle. The basic equation for such models is
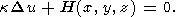 | (9) |
Here u(x, y, z) is temperature distribution in the crust, H(x, y, z) - the heat generation by ragioactive elements per unit volume. The elementary solution for a one-dimensional problem (this model is good enough in most of the applications, because the lateral variations of radiogenic elements concentrations in the stable crust are small comparing with the vertical trend) looks as
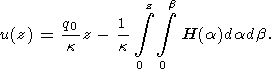 | (10) |
Here q0 is the surface heat flow density and k - the thermal conductivity. The surface heat flow density is related to the value of mantle heat flow qm by the following expression
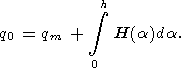 | (11) |
Here h is the thickness of the "radiogenic" layer in the upper crust.
Two types of function
H(z) are usually considered in geothermal applications.
The simplest one is equal to constant
H=H0>0 at
z
We assume here the viscous rheology for the rock matrix which seems to be a
reasonable approximation for the hot subcrustal mantle. A theory of viscous
consolidation takes into account flow of the matrix which occurs under the
stresses arising from the density difference between the
rock matrix and the fluid phase creating an interconnected network. This theory
predicts the spreading of non-linear porosity waves transporting the fluid
phase to the upper horizons. The geophysical applications of the viscous
consolidation theory originated from papers of
McKenzie [1984],
Richter and McKenzie [1984] and
Scott and Stevenson [1984]
allow to understand many aspects of magmatism and metamorphism (such as melt
uprising and focusing beneath the Mid-Ocean ridges, transport of fluids in
metamorphic environment). It is important to keep in mind that
this theory does not necessarily infer the mass transfer at the scale of
mineral grain which is usually called the pervasive flow, but can be valid
in describing the mass transfer at much larger scale. The
main requirement is that the spacing between the fluid conduits must be small
comparing to the characteristic dimension of the considered domain, so the
averaging of equation governing the flow of fluid and matrix could be done.
In this sense the consolidation theory might be applied to the
study of fluid transfer in the large system with spacing of cracks, say of an
order of 10 or 100 m. But at the scale of the distance between the neighbouring
conduits, the fluid transport would be seen as a channelized one. The theory of
viscous consolidation assumes the rock massif having some initial
permeability
K0 (and this is a controversial point in this theory),
which changes in the process of consolidation, including the rapid transport of
fluid with respect of the much more viscous rock matrix as well as the viscous
deformation of matrix itself. As some anomalous region of high porosity arises
in the rock massif, it is not able to resist the stresses, and deformation of
the matrix spreads upward in form of non-linear porosity waves. In the
approximation of a small porosity the dimensionless equations of viscous
consolidation theory reduce to the following equation for the
porosity or volume concentration of fluid (CO2 + some additional species
like KCl, NaCl)
F(x, y, z, t)
The scales for time
t0, length
l0 and hydrodynamic flow velocity
v0 are
Here
K0 is the initial permeability of rock massif,
F0 - the
initial permeability,
Dr - the density
difference between the rock
and fluid (in our case CO2 ),
g - the acceleration of gravity,
m - the viscosity of fluid and
h=hs
+ 4x/3 is the effective
viscosity of matrix, where
hs is viscosity
of matrix and
x - the
bulk viscosity responsible for the changing of porosity.
This equation has been intensively studied and there are many papers on this subject
followed the first publications of Barcilon and Richter [1986],
Richter and McKenzie [1984],
and Scott and Stevenson [1984, 1986]
(for a more
comprehensive view we refer to
Spiegelman [1993a, 1993b]). It
predicts the spreading of
solitary porosity waves or wave trains depending on the initial conditions. The
simplest 1-D non-linear solitary wave solution
[Barcilon and Lovera, 1989] has the implicit form
Here
f = F/F0=f(z) is the normalized distribution of porosity
(concentration of CO2 ),
z=z-ct, and
c is the wave velocity which
is simply related to the amplitude
A of non-linear wave
c=2A+l.
Although it was shown
[Barcilon and Lovera, 1989;
Khodakovskii et al., 1998;
Wiggins and Spiegelman, 1995]
that such a 1-D wave became unstable after some time and evolves to a group
of 2- or 3-D wave disturbances, we think that this solution can be used for an
estimation of the amount of CO2 and rate of its transfer to the base of
the crust as well as the related heat effects. The solitary
wave arises and spreads upward if the initial distribution of porosity
(concentration of CO2 ) corresponds to the function
The fluid flow velocity (the hydrodynamic velocity, not the D'Arcy one)
is determined easily in the approximation of low porosity
F
we get for
F = F0F(z) and
v=v0h(z)
a simple
equation
-cf'+(fh)'=0. Under condition that
f
which in dimensional form is seen as
Now we can estimate the amount of carbon dioxide transported by a solitary
wave by the integration
M is just the excess porosity. Notice that
M could be calculated as
M=2|I|,where
and integration is performed on the
f -domain. This integral is easily
calculated and the results is written as
Going to calculation of the amount of carbon dioxide which can be
transported by a non-linear solitary wave we should discuss the choosing the
values of the relevant physical parameters. The data on the density of carbon
dioxide under the elevated temperature and pressure were taken from
the paper of
Bottinga and Richet [1981]. For the temperature range
700-1300o C and corresponding range of pressure 7-27 kbar density
of
carbon dioxide changes in the limits - 1000-1530 kg/m3. For the crude
estimates the average value of about 1200 kg/m3 might be used. Viscosity
of CO2 fluid according to
Walther and Orville [1982]
lies in the range 1.0-1.5
The volume of CO2 stored in the pile with the cross section of l m
2 and transported by a solitary wave is estimated according to
V = MF0l0S0.
For
F0=10-2,
l0=100 m and
A=5 ( S0 =1 m2 ), we get
V=161 m3. For an area of
S
The thermal effects related to the propagation of non-linear porosity waves are
described by the energy conservation equation written in the co-ordinate system
fixed in the matrix. It should be written in this system because we are
interested in the evaluation of temperature rise at some level
coupled with the matrix. Neglecting the effect of the non-homogeneous
deformation of the matrix which is of the second order in
F0, the
equation of heat transport in dimensional form is written as
In non-dimensional form more convenient for numerical study it is seen as
Here
Ba is the non-dimensional parameter
Ba=a2t0/l20
= a2m3/2(K03/2h1/2Drg)-1 and
(rc)av
- the average value of the product of density and heat
capacity for the rock-fluid system, which it is very near to
rmcm
due to a small values of porosity. The last equation has been solved numerically
for the following set of parameters
A=5,
c=11,
F0=10-2,
Ba=0.455. The initial temperature distribution has been chosen as linear
one at the depths shallower than 70 km and reaching 1300o C at this
depth.
We also proposed temperature at the lower horizons to be equal to 1300oC
at the initial moment.
Returning to the point where we estimated the mass of CO2 required for
transformation of parental gneisses into charnockites (
So, the mechanism of CO2 transport by non-linear porosity waves could be
responsible for the transport of CO2 from the mantle depths to the crustal
levels, but the heating of the crust probably is not related to the direct
effect of fluid transfer.
Although there are different points of view for a possible source of carbon
dioxide providing the necessary condition for the formation of charnockites,
we believe the most natural explanation is related to the experimental data
on the melting of the carbonated peridotites
[Eggler, 1976;
Lee and Wyllie, 1998;
Wyllie and Huang, 1976.
These experiments predict the releasing of CO2 -rich fluid phase at the
depth ~70 km, corresponding to pressure of about 27 kbar. At larger
depths CO2 can not exist in the form of a separate phase and is
absorbed
by a partial melt or reacts with the silicate rocks to form dolomite being
a stable carbonate phase below the solidus at pressures more than
27 kbar. Rising up to the level of 70 km in the mantle the partial melts
associated with mantle plumes should release CO2 -rich fluid phase near
this level. There are indications for a much more intensive generation and
transport of carbonated melts in the Precambrian resulting in the formation
of large kimberlite bodies in the lower lithosphere as it was proposed by
P. Wyllie. Another indirect evidence comes from the fact that most of the large
alcaline complexes are of Proterozoic age. Finally, the recent data
( Janardhan, personal communication) show that many granitic bodies
found in charnockite environment and previously interpreted of being much
younger than charnockites, really have the same age. Our final conclusion is in
favour of the following scenario: CO2 is released from the mantle melts
at the depth near 70 km and transported by the non-linear
porosity waves to the base of the crust and further to the level where
charnockitization would start. The heat needed for temperature uprising is
supplied by the magma underplating. Uprising of low-viscosity partially melted
material could, in turn, create the real conduits for the non-linear waves.
Such a situation realises in the case of plume uprising through a relatively
cold lower lithosphere. In this case CO2 -rich fluid rapidly transported
upwards by a porosity waves in the low viscosity plume material, would create
the carbon dioxide-rich head of the plume. Flux of CO2 would come
to the crust almost contemporarily with the heating. In the case when the
lower lithosphere is hot enough to have a viscosity of an order of
1018 Pa
Barcilon V. and Lovera O., Solitary waves in magma dynamics,
J. Fluid Mech., 204, 121-133, 1989.
Barcilon V. and Richter F. M., Non-linear waves in compacting media,
J. Fluid Mech., 164, 429-448, 1986.
Bernard-Griffiths J., Jahn B. M. and Sen S. K., Sm-Nd isotopes and REE
geochemistry of Madras granulites, India: An Introductory statement,
Precamb. Res., 37, 343-353, 1987.
Bonafede M., Axisymmetric deformation of a thermo-elastic half-space:
inflation of a magma chamber, Geophyl. J. Inter., 103, (2),
289-299, 1990.
Bottinga Y. and Richet P., High pressure and temperature equation of state
and calculation of the thermodynamic properties of gaseous carbon dioxide,
American J. Sci., 281, 615-660, 1981.
Canil D., Experimental study bearing on the absence of carbonate in
mantle-derived xenoliths, Geology, 18, 1011-1013, 1990.
Connoly J. A. D., Devolatilization-generated fluid pressure and
deformation-propagated fluid flow during prograde regional metamorphism,
J. Geophys. Res., l02, (B8), 18,149-18,173, 1997.
Craword M. L and Hollister L. S., Metamorphic fluids: the evidence from fluid
inclusions. In: Fluid-Rock Interactions during Metamorphism,
J. V. Walther and J. V. Wood (Eds.), pp. 1-35, Springer-Verlag,
1986.
Dobretzov N. L., The global petrology, 277 p., Nauka, Moscow,
1977, (in Russian).
Dunai T. J. and Touret J. L. R., A noble gas study of a granulite sample from
Nilgiri Hills, southern India: implications for granulite formation,
Earth and Planet. Sci. Lett., 119, 271-281, 1993.
Eggler D. H., Composition of the partial melt of carbonated peridotite in the
system CaO-MgO-SiO2-CO2, v. 75, pp. 623-626,
Carnegie Inst. Washington Yearbook, 1976.
Ganguly J., Singh R. N. and Ramana D. V., Thermal perturbation during
charnockitization and granulite facies metamorphism in southern India,
J. Metamorphic Geol., 13, 419-430, 1995.
Glassley W. E., Deep crustal carbonates as CO
2 fluid sources: evidence
from metasomatic reaction zones, Contib. Min. Petr., 84, 15-24, 1983.
Gupta M. L., Sunder A. and Sharma S. R., Heat flow and heat generation
in the
Archean Dharwar cratons and implications for the Southern Indian Shield geotherm
and lithospheric thickness, Tectonophysics, 194, (1/2), 107-122, 1991.
Hansen E. G., Janardhan A. S., Newton R. C., Frame W. K. B. N.
and
Ravindra Kumar G. R., Arrested charnockite formation in southern India
and
Sri Lanka, Contrib. Min. Petrol., 96, 225-244, 1987.
Harris N. B. W., Holt R. W. and Drury S. A., Geobarometry, geothermometry
and late Archean geotherms from the granulite facies terrain of South India,
J. Geol., 90, 509-528, 1982.
Hopgood A. M. and Bowes D. R., Contrasting structural features in the
granulite-gneiss-charnockite complex, Lake Baikal, U.S.S.R.: evidence of
diverse geotectonic regimes in early Proterozoic
times, Tectonophysics, 174, 279-299, 1990.
Ionov D. A., Dupuy C., O'Reilly S. Y., Kopylova M. G. and Genshaft Y. S.,
Carbonated peridotite xenoliths from Spitsbergen: implications of trace
element signature of mantle carbonate metasomatism,
Earth Planet. Sci. Letters, 119, 283-297, 1993.
Jackson D. H., Mattey D. P. and Harris N. B. W., Carbon isotope compositions
of fluid inclusions in charnockites from the southern India, Nature, 333,
167-170, 1988.
Janardhan A. S., Newton R. C. and Smith J. V., Ancient crustal metamorphism
of low P
H2 O charnockite
formation of Kabbaldurga, South India,
Nature, 278, 511-514, 1979.
Janardhan A. S., Newton R. C. and Hansen E. C., The transformation of
amphibole facies gneiss to charnockite in southern Kamataka and northern
Tamil Nadu, India, Contrib. Min. Petrol, 79, 130-149, 1982.
Jessop A. M. and Lewis T., Heat flow and heat generation in the Superior
Province of the Canadian Shield, Tectonophysics, 5, 55-77, 1978.
Jiang J., Clayton R. N. and Newton R. C., Fluids in granulite metamorphism:
a comparative oxygen isotope study of the south India and Adirondack high-grade
terraines, J. Geol., 96, 517-533, 1988.
Jones A. P. and Wyllie P. J., Paragenetic trends of oxide minerals in
carbonate-rich kimberlites with new analysis from the Benfontein sill,
South Africa, J. Petrol., 26, 210-222, 1985.
Khodakovskii G., Rabinowicz M., Genthon P. and Celuleneer G., 2D Modeling
of melt percolation in the mantle: the role of a melt dependent mush viscosity,
Geophys. Res. Lett., 25, 683-686, 1998.
Kreulen R. and Schuiling R. D., Are thermal domes heated by CO
2 -rich
fluids from the mantle?, Earth and Planet. Sci. Lett., 43, 298-302, 1979.
Kreulen R. and Schuiling R. D., N2CH4 - CO2 fluids during
formation of the Dome De L'Agout, France, Geochim. Cosmoch. Acta, 46,
193-203, 1982.
Le Bas M. J., Carbonatite-Nephelmite Volcanism, 395 pp., London, John
Willey,
1977.
Lee W.-J. and Wyllie P. J., Petrogenesis of carbonatite magmas from mantle
to crust, constrained by the system CaO-(MgO + FeO
Mahabaleswar B., Geothermobarometry along the North - South Transect - a
review. In: "Continental crust of South India", B. P. Radiiakrishna
(Ed.),
pp. 303-312, Geol. Soc., India, Bangalore, 1993.
Mahadevan T. M., Deep Continental Structure of India: A Review, 562 pp.,
Geol. Soc., India, Bangalore, 1994.
Mareschal J.-C. and West G. F., A model for Archean tectonism, Part 2,
Numerical models of vertical tectonism in greenstone belts, Canadian J. Earth
Sci., 17, 60-71, 1980.
McKenzie D., The generation and compaction of partially molten rock,
J. Petrol, 25, part 3, 713-765, 1984.
Mohan A., Prakash D. and Sachan H. K., Fluid inclusions in charnockites
from
Kodaikanal massif (South India): P-T record and implications for crustal
uplift history, Min. and Petrol., 57, 167-184, 1996.
Mueller R. F. and Saxena S. K., Chemical Petrology, 378 pp.,
Springer-Verlag. 1977.
Natale G., Salusti E. and Troisi A., Rock deformation and fracturing processes
due to nonlinear shock waves propagating in hyperthermal fluid pressurized
domain, J. Geophys. Res., 103, (B7), 15,325-15,338, 1998.
Newton R. C., Nature and origin of fluids in granulite facies
matamorphism, J. Geol. Soc. lndia, 31, 1003-1012, 1983.
Newton R. C., Metamorphic fluids in deep crust, Ann. Rev. Earth Planet. Sci.,
17, 385-412, 1988.
Newton R. C., Smith J. V. and Windley B. F., Carbonic metamorphism, granulites
and crustal growth, Nature, 288, 45-50, 1980.
Philpotts A. R., Principles of igneous and metamorphic petrology,
484 pp., Prentice-Hall Intern. Inc., Englewood Ciffs, 1990.
Pichamuthu C. S., The charnockites of South India, Proc. Pan. Indian Ocean Sci.
Cong, pp. 50-51, Perth, Sec. C-C, 1954.
Radhakrishna B. P., Ramakrishnan M. and Mahabaleswar B. (Eds.), Granulites
of South India, Puchamuthu volume, 502 pp., Geol. Soc. India. Bangalore,
1990.
Radhakrishna B. P., (Ed.), Continental crust of South India, 497 pp.,
Geol. Soc. India, Bangalore, 1993.
Raith M., Raase P., Ackermand D. and Lal R. K., Regional geothermobarometry
in the granulite facies terrane of south India, Trans. R. Soc. Edinburgh, Earth
Sci., 73, 221-244, 1983.
Ravindra Kumar G. R., Srikantappa C. and Hanson E., Chamockite formation
at
Pohmudi in Southern India, In: Continental crust of South India,
pp. 251-256, B. P. Radhakrishna (Ed.), Geol. Soc. India, Bangalore,
1993.
Richter F. and McKenzie D., Dynamical models for melt segregation from a
deformable matrix, J. Geol., 92, 729-740, 1984.
Santosh M., Fluid inclusions palaeopressures and source of carbonic fluids in
the massive charnockites of Kerala, South India, Mem. Geol. Soc. India, 11,
91-99, 1988.
Santosh M., Jackson D.H., Harris N. B. W. and Mattey D. P.,
Carbonic fluid
inclusions in south Indian granulites: evidence for entrapment during
charnockite formation, Contrib. Min. Petrol, l08, 318-330, 1991.
Scott D. and Stevenson D., Magma solitons, Geophys. Res. Lett., 11,
1161-1164, 1984.
Scott D. and Stevenson D., Magma ascent by porous flow, J. Geophys. Res.,
91, 9283-9296, 1986.
Singh R. N. and Negi J. G., On the estimation of vertical distribution of
radiogenic heat production in the crust, Geophys. J., 62, (1),
221-224, 1980.
Sobolev S. V., 3-D mantle temperature and dynamics of the French Massif
Central from integrated interpretation of seismic tomography, mantle
xenoliths and surface heat flow, Annales Geophys., 16, (S1), p. 90,
1998.
Spiegelman M., Flow in deformable porous media, Part 1, Simple analysis,
J. Fluid Mech., 247, 17-38, 1993a.
Spiegelman M., Flow in deformable porous media, Part 2, Numerical analysis -
the relationship between shock waves and solitary waves, J. Fluid Mech., 247,
39-63, 1993b.
Srikantappa C., High pressure charnockites of the Nilgiri Hills, Southern India,
In: Continental crust of South India, B. P. Radhakrishna (Ed.),
pp. 95-112, Geol. Soc. India, Bangalore, 1993.
Srikantappa C., Reith M. and Spierling B., Progressive charnockitizalion of
a leptynite - khondalite suite in southern Kerala, India - Evidence for
formation of charnockites through decrease in fluid pressure,
J. Geol. Soc. India, 26, 849-872, 1985.
Srikantappa C., Reith M. and Touret J. L. R., Synmetamorphic high-density
carbonic fluids in the lower crust: evidence from the Nilgiri granulites,
southern India, J. Petrol, 4, 733-760, 1992.
Stahle H. J., Raith M., Hoerness S. and Delfs A., Element mobility during
incipient granulite formation at Kabbaldurga, southern India,
J. Petrol., 28, 803-834, 1987.
Touret J. L. R., Nature and interpretation of fluid inclusions in granulites,
J. Geol. Soc. India, 31, (1), 158-160, 1988.
Touret J. L. R., Vladaar N. M. and Weerhoten P., Role of CO
2 - bearing
fluids in granulite formation, Acta Geophysicae, S1, 99 pp., 1997.
Walther I. V. and Orville P. M., Volatile production and transport in regional
metamorphism, Contrib. Miner. Petr., 79, 252-257, 1982.
West G. F. and Mareschal J.-C., A model for Archean tectonism, Part I,
The thermal conditions, Canadian J. Earth Sci., 16, 1942-1950, 1979.
Wiggins Ch. and Spiegelman M., Magma migration and magmatic solitary waves
in 3-D, Geophys. Res. Lett., 22, 1289-1292, 1995.
Wyllie P. J. and Huang W. L., Carbonation and melting reactions in the system
CaO-MgO-SiO2-CO2 at mantle pressures with geophysical and
petrological applications, Conrib. Min. Petrol., 54, 79-107, 1976.
 h
for the simplest model. We calculated
temperature at the depth 30 km Tin, which is of present interest,
for the model with constant heat production in the upper high
radioactive layer assuming the thickness of this layer to be equal to 10 km.
The value 2.4 W
h
for the simplest model. We calculated
temperature at the depth 30 km Tin, which is of present interest,
for the model with constant heat production in the upper high
radioactive layer assuming the thickness of this layer to be equal to 10 km.
The value 2.4 W m-1
m-1 K-1
has been taken for the thermal
conductivity of crustal rocks. The following values of temperature
Tin have been obtained - 474oC for
H0 = 4.2m W/m3,
498o C for
H0 = 5.8
m W/m3 and 544o C for
H0 = 8
m W/m3.
These estimates may be considered as upper bounds because
the corresponding temperatures at the Moho (the available geological data and
geophysical reasons point out the thickness of the late Archean crust not
to differ significantly from the present average 40 km) - 598oC,
623oC
and 669oC - would be very close or even a little higher than the solidus
temperature of felsic rocks in the presence of water. For the model with
exponential distribution of radiogenic elements, the same values of
H0 and reasonable values of
D the conclusion is the same - the crust
at the levels of charnockitization must be heated at least for a 300oC or
even more. Taking into account the width of the charnockitization zones
(many kilometers), we can not believe that such a heating could be provided
by shear heating. The only reasonable cause in view of recent data can
be related to underplating of hot material.
K-1
has been taken for the thermal
conductivity of crustal rocks. The following values of temperature
Tin have been obtained - 474oC for
H0 = 4.2m W/m3,
498o C for
H0 = 5.8
m W/m3 and 544o C for
H0 = 8
m W/m3.
These estimates may be considered as upper bounds because
the corresponding temperatures at the Moho (the available geological data and
geophysical reasons point out the thickness of the late Archean crust not
to differ significantly from the present average 40 km) - 598oC,
623oC
and 669oC - would be very close or even a little higher than the solidus
temperature of felsic rocks in the presence of water. For the model with
exponential distribution of radiogenic elements, the same values of
H0 and reasonable values of
D the conclusion is the same - the crust
at the levels of charnockitization must be heated at least for a 300oC or
even more. Taking into account the width of the charnockitization zones
(many kilometers), we can not believe that such a heating could be provided
by shear heating. The only reasonable cause in view of recent data can
be related to underplating of hot material.
5. Mechanism of Viscous Consolidation and Transport
of Carbon
Dioxide by Non-Linear Porosity Waves
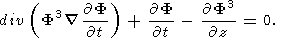
(12) 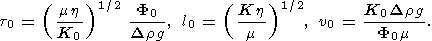
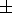 z=F(f,A)
z=F(f,A)
(13) 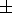 z = F(f0).
z = F(f0).
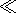 1. From
the equation of continuity for a fluid
1. From
the equation of continuity for a fluid
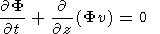
(14)  1 at
z
1 at
z
 (porosity must approach the undisturbed value
f=l )
and
h
(porosity must approach the undisturbed value
f=l )
and
h 1 (the fluid flow velocity
v must come to the value
v0, corresponding to the filtration through the
matrix with the initial
porosity
F0 ) we obtain
1 (the fluid flow velocity
v must come to the value
v0, corresponding to the filtration through the
matrix with the initial
porosity
F0 ) we obtain
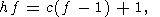
(15) 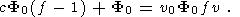
(16) 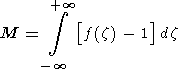
(17) 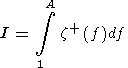
(18) 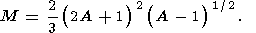
(19) 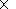 10-5 Pa
10-5 Pa s,
and we used the
lower value although a changing the viscosity in a one and half times does not
influence the result. The initial permeability
K0 has been taken as low
as 10-19 m2. The more disputable are the values
of effective viscosity of the matrix
h and the normal volume concentration
of CO2. We consider the value l018 Pa
s,
and we used the
lower value although a changing the viscosity in a one and half times does not
influence the result. The initial permeability
K0 has been taken as low
as 10-19 m2. The more disputable are the values
of effective viscosity of the matrix
h and the normal volume concentration
of CO2. We consider the value l018 Pa s
a good approximation
to the viscosity of the hot subcrustal Archean mantle, especially if the
underplating has taken place just before the main metamorphic event. The value
0.01 has been taken for
F0, which corresponds
approximately to 0.003 wt %
of CO2. The characteristic scales under the parameters given
above would
be
l0
s
a good approximation
to the viscosity of the hot subcrustal Archean mantle, especially if the
underplating has taken place just before the main metamorphic event. The value
0.01 has been taken for
F0, which corresponds
approximately to 0.003 wt %
of CO2. The characteristic scales under the parameters given
above would
be
l0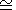 100 m,
100 m,
 t0
t0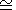 150 yr and
v0
150 yr and
v0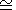 0.67 m/yr.
The amplitude A could be different depending on the initial condition.
Spreading of a solitary compaction wave is illustrated by Figure 1 where profiles
of porosity for the case
A = 5.4 are shown for subsequent moments of time
with time interval
Dt = 2.5t0.
It is easy to see that the wave
passes the first 20 km only for 17.5
0.67 m/yr.
The amplitude A could be different depending on the initial condition.
Spreading of a solitary compaction wave is illustrated by Figure 1 where profiles
of porosity for the case
A = 5.4 are shown for subsequent moments of time
with time interval
Dt = 2.5t0.
It is easy to see that the wave
passes the first 20 km only for 17.5
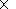 150 yr = 2625 yr.
150 yr = 2625 yr.
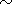 1.5
1.5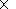 105 km2, the total mass
of CO2, transported by a solitary wave is estimated as
2.4
105 km2, the total mass
of CO2, transported by a solitary wave is estimated as
2.4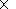 1013( m3)
1013( m3)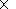 r CO2
r CO2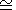 2.6
2.6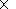 1016 kg.
It should be compared with the amount required from the viewpoint of
geochemistry. We estimated above this amount as 0.97-1.93 wt %. It means that
for a pile of 1 m2 cross-section and height of 10 km the required
amount
of CO2 would be ~106 kg and for an area with the surface of
S
1016 kg.
It should be compared with the amount required from the viewpoint of
geochemistry. We estimated above this amount as 0.97-1.93 wt %. It means that
for a pile of 1 m2 cross-section and height of 10 km the required
amount
of CO2 would be ~106 kg and for an area with the surface of
S 1.5
1.5 105 km
2 it results in 1.2
105 km
2 it results in 1.2 1017 kg. This
mass of CO2 could be transported by only 6 subsequent solitary waves
related to 6 pulses of fluid activity.
1017 kg. This
mass of CO2 could be transported by only 6 subsequent solitary waves
related to 6 pulses of fluid activity.
6. Thermal Effects Related to the Transport of CO2 by
Non-Linear Porosity Waves
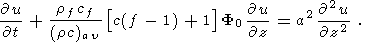
(20) 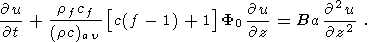
(21)  The heat transfer equation has been solved by a finite-difference method,
and the results of calculation are demonstrated at Figure 2. The lowermost
curve 1 depicts the excess temperature profile at moment
t1=10
The heat transfer equation has been solved by a finite-difference method,
and the results of calculation are demonstrated at Figure 2. The lowermost
curve 1 depicts the excess temperature profile at moment
t1=10 t0=1500 yr.
Other curves illustrate the progressive
heating of the lithosphere and represent the excess temperature profiles for
the subsequent moments of time with interval
Dt=5t0
beginning
from the moment
t=t1. Curve 5 at Figure 2 corresponds
to the moment
t=30t0=4500 yr.
t0=1500 yr.
Other curves illustrate the progressive
heating of the lithosphere and represent the excess temperature profiles for
the subsequent moments of time with interval
Dt=5t0
beginning
from the moment
t=t1. Curve 5 at Figure 2 corresponds
to the moment
t=30t0=4500 yr.
 The maximum thermal perturbation which could be achieved at the
base of the crust is around 5o C (see curve 1 at Figure 3,
corresponding to the moment
t=60t0=9000 yr),
and such
a signal comes from the depth of 70 km for the time
The maximum thermal perturbation which could be achieved at the
base of the crust is around 5o C (see curve 1 at Figure 3,
corresponding to the moment
t=60t0=9000 yr),
and such
a signal comes from the depth of 70 km for the time
 104 yr.
For comparison, the thermal effect from the wave of larger amplitude
(A=10) is illustrated by curve 2.
104 yr.
For comparison, the thermal effect from the wave of larger amplitude
(A=10) is illustrated by curve 2.
 1.2
1.2 1017 kg
for a 10 km thick charnockitic layer occupying the area
S
1017 kg
for a 10 km thick charnockitic layer occupying the area
S 1.5
1.5 105 km2 )
and conclusion that such a mass of CO2
could be transported by the sequence of only 6 solitary
waves, we see that such
a sequence would provide the temperature rise no more than 25oC. This
result is quite clear from the physical point of view - as it was shown by
Ganguly et al. [1995], the mass of CO2 needed to heat the
crust under the area of the same surface ( S
105 km2 )
and conclusion that such a mass of CO2
could be transported by the sequence of only 6 solitary
waves, we see that such
a sequence would provide the temperature rise no more than 25oC. This
result is quite clear from the physical point of view - as it was shown by
Ganguly et al. [1995], the mass of CO2 needed to heat the
crust under the area of the same surface ( S 1.5
1.5 105 km
2 ) up to the
conditions of the granulite facies should be around
18
105 km
2 ) up to the
conditions of the granulite facies should be around
18 1018 kg, which
is almost two order less than the mass transported by the considered sequence
of waves.
1018 kg, which
is almost two order less than the mass transported by the considered sequence
of waves.
7. Conclusive Discussion: Source of the Carbon Dioxide,
Magma Underplating and Exsolution of CO2
 s,
carbon dioxide could be transported by non-linear
porosity waves independently from the motion of the partially melted material.
The signature of underplating of hot material could not be necessarily result
in high seismic velocities in the lower crust and subcrustal mantle. So, the
petrological interpretation of DSS data for the crust of
the charnockitic province in the southern India based probably on papers of
Sobolev [1998 and some earliar publications] could be
very
fruitful. Concerning the transport of CO2 phase at the higher levels in
the brittle crust we can propose an active role of hydrofracturing and
poroelastic waves.
s,
carbon dioxide could be transported by non-linear
porosity waves independently from the motion of the partially melted material.
The signature of underplating of hot material could not be necessarily result
in high seismic velocities in the lower crust and subcrustal mantle. So, the
petrological interpretation of DSS data for the crust of
the charnockitic province in the southern India based probably on papers of
Sobolev [1998 and some earliar publications] could be
very
fruitful. Concerning the transport of CO2 phase at the higher levels in
the brittle crust we can propose an active role of hydrofracturing and
poroelastic waves.
Acknowledgments
This work was done under ILTP program of Indo-Russian collaboration. A.O.G.
is grateful to Department of Science and Technology, India, for providing a
fellowship to visit C-MMACS and to Prof. V. K. Gaur, Earth Sciences Area
Co-ordinator from the Indian side, for the support of this project.
A.O.G. is indebted to Prof. T. S. Prahlad, director of NAL and also all
the
staff of C-MMACS for their help and support during his staying in Bangalore.
The authors would like to thank Prof. A. S. Janardhan for fruitful discussions.
References
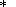 )-(Na2O + K2O)-(SiO2
+ Al2O3 + TiO2 )-CO2,
J. Petrol., 39, 495-517, 1998.
)-(Na2O + K2O)-(SiO2
+ Al2O3 + TiO2 )-CO2,
J. Petrol., 39, 495-517, 1998.
Load files for print and local use.
This document was generated by TeXWeb
(Win32, v.1.0) on November 24, 1999.
