Neogaean paleomagnetism constraints on the processes at
the core and surface of the Earth
D. M. Pechersky
Part 2. Comparison of Processes at the Core and Earth's
Surface
According to the present concept of geodynamics, processes at the Earth's
surface and in its lithosphere,
mantle, and core are closely interrelated (see Introduction),
which gave rise to the concept of geonomic periodicity
[Khramov and Kravchinskii, 1984;
Kravchinskii, 1977]
stating that all phenomena of the same
rank are essentially equivalent. This provides means for a quantitative
description of one phenomenon or
process in terms of another (conjugation principle).
Unfortunately, most surface processes either cannot be
quantified or available information does not embrace even the Phanerozoic.
Paleomagnetic data provide the
opportunity for the most complete quantitative description of the movement
of large continental blocks in the
Neogaea. In view of this, I addressed the best documented, measurable
geological information, namely biota
evolution, chronostratigraphy, and motion of continental plates.
Since the frequency of geomagnetic field sign
changes, predominance of one of polarities, and relative changes
in paleointensity correlate with each other
and are synchronous (see Figure 1, part 1; also
[Pechersky and Didenko, 1995], we will use data on the
reversal frequency which are most representative.
Changes in the Organic World and Geomagnetic Reversal Frequency
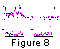 To compare the geomagnetic field behavior with changes in
the organic world,
I used (1) changes in the
number of units in the chronostratigraphic scale (Figure 8a),
(2) changes in the diversity of families of marine
organisms, and (3) extinctions of marine organism families that occurred every
10 Myr (Figure 8c). The
chronostratigraphic scale of Harland et al. [1990]
with certain modifications (see Part 1) was used for the
discussion of topic (1), and topics (2) and (3) will be discussed on
the basis of the Phanerozoic summary
presented by Benton [1995] (unfortunately, data on
the Riphean are not so representative); only the data on
marine organisms were used because they are more representative of the whole
Phanerozoic. All data are
correlated with the general geological time scale.
To compare the geomagnetic field behavior with changes in
the organic world,
I used (1) changes in the
number of units in the chronostratigraphic scale (Figure 8a),
(2) changes in the diversity of families of marine
organisms, and (3) extinctions of marine organism families that occurred every
10 Myr (Figure 8c). The
chronostratigraphic scale of Harland et al. [1990]
with certain modifications (see Part 1) was used for the
discussion of topic (1), and topics (2) and (3) will be discussed on
the basis of the Phanerozoic summary
presented by Benton [1995] (unfortunately, data on
the Riphean are not so representative); only the data on
marine organisms were used because they are more representative of the whole
Phanerozoic. All data are
correlated with the general geological time scale.
The following regularities on three time scales have been revealed.
(1) Regularity of the first order (the whole Neogaea):
a sharp difference
in the differentiation degree of the
chronostratigraphic and magnetostratigraphic scales in the Riphean and
Vendian-Phanerozoic (Figures 1 and
8), which is consistent with a rapid progress in
the development of diverse life forms beginning from the Vendian-Cambrian.
(2) Regularity of the second order (geological eras):
geological eras begin
later than reversal frequency
minimums all over the Neogaea
[Khramov et al., 1982;
Molostovskii et al., 1976;
Pechersky and Didenko, 1995].
This delay ranging from 35 to 60 Myr (Figure 1) averages
35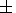 10 Myr, which yields 4-10 cm/yr for
the energy transfer rate from the core-mantle boundary to surface, i.e.,
for the mantle convection velocity.
This value agrees with average velocities estimated for the drift of
main continental plates (see below)
[Jurdy et al., 1995;
Zonenshain et al., 1987].
Therefore boundaries of geological eras are primarily related to an inner
geodynamic mechanism.
10 Myr, which yields 4-10 cm/yr for
the energy transfer rate from the core-mantle boundary to surface, i.e.,
for the mantle convection velocity.
This value agrees with average velocities estimated for the drift of
main continental plates (see below)
[Jurdy et al., 1995;
Zonenshain et al., 1987].
Therefore boundaries of geological eras are primarily related to an inner
geodynamic mechanism.
(3) Regularity of third order (comparable with geological
periods):
minimums and maximums nearly coincide,
which implies changes in the organic world to be synchronous with
variations in the polarity reversal
frequency and geomagnetic paleointensity; this synchronism is most distinct
in the Phanerozoic (Figures 1 and
8). Thus, the difference between maximums (minimums) of reversal frequency
and the nearest maximums
(minimums) of numbers of stratigraphic units, diversity changes,
and extinctions of organisms amounts to
3.1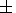 9.6,
3.5
9.6,
3.5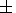 6.3 ,
and
1.4
6.3 ,
and
1.4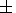 9.5 Myr, respectively. Moreover, many boundaries
of
geological periods coincide
with narrow minimums less than 10 Myr wide or with slight kinks
in reversal frequency and/or paleointensity
variations (Figure 1) which are smoothed away upon the 30-Myr
averaging (Figure 1).
Some differences in
variation rates of the organic world and reversal frequency are
likely to be related to deficient
magnetostratigraphic information and dating uncertainties.
9.5 Myr, respectively. Moreover, many boundaries
of
geological periods coincide
with narrow minimums less than 10 Myr wide or with slight kinks
in reversal frequency and/or paleointensity
variations (Figure 1) which are smoothed away upon the 30-Myr
averaging (Figure 1).
Some differences in
variation rates of the organic world and reversal frequency are
likely to be related to deficient
magnetostratigraphic information and dating uncertainties.
Thus, acceleration and deceleration of core-mantle boundary
processes
and evolution of the organic world
occur synchronously; boundaries between geological periods are mostly
associated with drops in the reversal
frequency and geomagnetic paleointensity (but not with individual reversals!)
and themselves often mark a
slowdown in the evolution of organic world (Figures 1 and 8).
 If large long-period field variations directly affect changes
in the organic
world, strong (direct or inverse)
correlation should exist between synchronous variations in characteristics
of organic world and geomagnetic
field, in particular, reversal frequency. However, numerical estimates
do not confirm such a correlation, as is
evident from Figure 9. Consequently, an immediate effect of long-period
field variations on changes in the
organic world is either absent or insignificant, and only their cyclicities
coincide.
If large long-period field variations directly affect changes
in the organic
world, strong (direct or inverse)
correlation should exist between synchronous variations in characteristics
of organic world and geomagnetic
field, in particular, reversal frequency. However, numerical estimates
do not confirm such a correlation, as is
evident from Figure 9. Consequently, an immediate effect of long-period
field variations on changes in the
organic world is either absent or insignificant, and only their cyclicities
coincide.
Thus, the comparison of variation rates of organic world and geomagnetic
field demonstrates that processes on
a geological time scale, as well as shorter processes, which occur near
the core and surface, are virtually
synchronous, but they are not connected with each other or,
speaking more cautiously, their interrelation is
obviously secondary and not causative: the processes "respond" to a common
external mechanism producing,
for example, changes in the rotation axis angle and/or angular velocity
of the Earth, which in turn
synchronously affect movements in the core and lower mantle,
producing changes in the geomagnetic field,
and tectonic, climatic and other processes at the surface, producing
changes in the state of biosphere. It is only
geodynamic processes on a scale of geological eras that are related
to the internal mechanism of upward
energy transfer from the lowermost mantle (possibly through convection,
plume ascent, etc.)
Horizontal Velocities of Continental Plates
The analysis of movements of tectonic blocks usually includes the
following procedures: construction of the
apparent pole wander path (APWP) of a given block over a specific geological
time interval from
paleomagnetic directions; spatial paleoreconstructions of a block
(and adjacent blocks) for various time
intervals, including the positioning of Euler poles of rotation;
and determination of the block velocity for
various time intervals from the motion of a certain point of the block.
The reconstructions are based on
tectonic, paleogeographic, paleoclimatic, and other evidence, position of
hotspots, and balance of forces that
affect the plate motion (slab pull in subduction zones,
pull-apart forces at mid-ocean ridges, etc.)
[Zonenshain et al., 1987].
Phanerozoic position of six continental plates
(Africa, Antarctic, Europe, Siberia, India, and
North America) has been recently reconstructed, and their velocities
have been estimated
[Jurdy et al., 1995].
However, paleoreconstruction of relative and especially absolute positions
of the plates are rather ambiguous
(particularly in the Precambrian). This is one of reasons why paleotectonic
reconstructions of continental
plates are not used here. However, the main reason is that this work
addresses global regularities in tectonic
motions rather than movements of separate blocks.
The motion of continents across the Earth's surface
resembles that of ice blocks during an ice drift: as a whole, those move
downstream, although individual
blocks may have different velocities, rotate in various senses and
at various angular velocities, stop, and even
move upstream, but the movements of each separate ice block have little
in common with general regularities
of the flow which are main concern of this paper. Therefore,
to simplify the problem I will consider separately
the latitude (constrained by paleomagnetic inclination) and rotational
(constrained by paleomagnetic
declination) components of the block velocity with respect to a point
in the vicinity of its center as is readily
done from its APWP. I used primarily the longest APWPs of various continental
blocks, reconstructed by
various authors and published reviews of paleomagnetic pole positions.
The data collection included the
following regions (the time series data and coordinates of the plate "center"
are presented in parentheses):
Australia (1700-0 Ma; 25o S, 135o E), Africa (720, 550-0 Ma;
0o S, 30o E), Europe (1700-0 Ma; 55o N,
35o E), India (1000, 820-750, 600-0 Ma; 20o N, 80o
E),
North America+Greenland (1300-1140, 1120-0 Ma; 40o N, 255o
E),
northern China (580-0 Ma; 45o N, 120o E), southern China
(600-550, 450-0 Ma; 30o N, 110o E), and Siberia
(1100-840, 730, 640-0 Ma; 60o N, 105o E)
[Dawson and Hargraves, 1994;
Elming et al., 1993;
Embleton, 1984;
Enkin et al., 1992;
Gordon et al., 1984;
Hyodo and Dunlop, 1993;
Idnurm and Giddings, 1988;
Khramov, 1991;
Klootvijk, 1984;
Lin et al., 1985;
Meert and Van der Voo, 1996;
Park et al., 1995;
Park and Gower, 1996;
Pechersky and Didenko, 1995;
Piper, 1995;
Pisarevsky et al., 1997;
Radhakrishna and Joseph, 1996;
Radhakrishna and Mathew, 1996;
Saradeth et al., 1989;
Seguin and Zhai, 1992;
Shapiro et al., 1997;
Smethurst et al., 1998;
Tarling and Abdeldayem, 1996;
Torsvik et al., 1992;
Van der Voo, 1988, 1990;
Van der Voo and Meert, 1991;
Wu et al., 1993;
Zhao et al., 1990, 1993].
 The data collected were revised and generalized.
Paleomagnetic determinations close in age are sometimes
strongly divergent and give abnormally high velocities.
These are mostly data from the Early and Middle
Riphean of Africa, India, and North America.
Such intervals were rejected. Paleolatitude, paleoinclination,
paleolatitude component of the plate motion velocity,
and angular velocity of paleoinclination variation
(rotation about a fixed point of a plate) were calculated
at centers of each plate for every 10-Myr APWP
interval. To remove possible errors, the results were averaged
with a smoothing window of 30 Myr. These data
were used for the calculation of mean paleolatitude velocities
of plate motion
Vpl (Figure 10a) and
rotation
VD (Figure 10b), as well as standard deviations from
these means
dVpl and
VD.
The means were calculated for eight plates in the Phanerozoic,
five plates in the Vendian-Late Riphean, three
in the Middle Riphean, and two in the Early Riphean.
The data collected were revised and generalized.
Paleomagnetic determinations close in age are sometimes
strongly divergent and give abnormally high velocities.
These are mostly data from the Early and Middle
Riphean of Africa, India, and North America.
Such intervals were rejected. Paleolatitude, paleoinclination,
paleolatitude component of the plate motion velocity,
and angular velocity of paleoinclination variation
(rotation about a fixed point of a plate) were calculated
at centers of each plate for every 10-Myr APWP
interval. To remove possible errors, the results were averaged
with a smoothing window of 30 Myr. These data
were used for the calculation of mean paleolatitude velocities
of plate motion
Vpl (Figure 10a) and
rotation
VD (Figure 10b), as well as standard deviations from
these means
dVpl and
VD.
The means were calculated for eight plates in the Phanerozoic,
five plates in the Vendian-Late Riphean, three
in the Middle Riphean, and two in the Early Riphean.
 The above comparison with an ice drift is clearly illustrated in Figure 11:
the majority continents move, with
slight variations, consistently, which is most evident beginning from
the mid-Paleozoic, but opposite
movements (for example, Europe, Siberia, North America, and Australia
in a 1100-900-Ma interval) are also
observed. The tendency mentioned in the Introduction is also evident from
the figure: concentration of most
continents in the equatorial zone at the time of existence
of Riphean Pangea and their divergence in the Early
Paleozoic (breakup of Paleozoic Pangea) followed by movement
of Laurasian continents to northern latitudes
and movement of Gondwana continents to the equator and southern latitudes
in the Mesozoic-Cenozoic.
The above comparison with an ice drift is clearly illustrated in Figure 11:
the majority continents move, with
slight variations, consistently, which is most evident beginning from
the mid-Paleozoic, but opposite
movements (for example, Europe, Siberia, North America, and Australia
in a 1100-900-Ma interval) are also
observed. The tendency mentioned in the Introduction is also evident from
the figure: concentration of most
continents in the equatorial zone at the time of existence
of Riphean Pangea and their divergence in the Early
Paleozoic (breakup of Paleozoic Pangea) followed by movement
of Laurasian continents to northern latitudes
and movement of Gondwana continents to the equator and southern latitudes
in the Mesozoic-Cenozoic.
The velocity pattern of the paleolatitude plate motion component
is most distinct (Figure 10a), virtually
coinciding with that of the full mean velocities calculated from
the spatial reconstruction of Phanerozoic
continents (Figure 10c)
[Jurdy et al., 1995],
although the sets of continents (and their number) are different.
Hence,
Vpl is likely to rather adequately reflect the variation
in the velocity moduli of continents in the
Phanerozoic and Precambrian. Figure 10a clearly shows a cyclicity in
Vpl disturbed by less regular plate
rotations (Figure 10b).
A sharp difference in the behavior of
VD and
dVD in
intervals of 1700-900 and 900-0 Ma. In the
first interval,
VD has a low scatter and varies rather periodically
(with maximums of
dVD at 1100
and 980 Ma); in the second interval, both velocity and its scatter gradually
increase toward the center of the
interval and then gradually decrease. The scatters appear to be minimum
during the existence of
supercontinents. The
Vpl pattern is different:
its behavior, with minor deviations, is similar throughout
the Neogaea and exhibits a regular change in mean velocities
from their minimum (10-20 km/Myr) to
maximum (40-60 km/Myr) values rarely (in the Riphean) reaching 80 km/Myr.
On the other hand, specific
behavior of
dVpl is observed in the Riphean, where the scatter
varies in the same manner as
Vpl, and
in the upper half of the Late Riphean-Phanerozoic, where their variations
are different, but the most
important is the relation
dVpl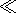 Vpl.
Against this background, an interval of "disturbed cyclicity" of
Vpl and high
dVpl values is clearly observed in the Vendian-uppermost
Riphean (650-530 Ma). Based on
direct measurements of intervals between adjacent maximums (minimums)
and wavelet analysis results (D. K. Galyagin and P. G. Frik),
the following characteristic times are recognized in the cyclicity of
Vpl,
dVpl,
VD, and
dVD : 20-30, 40-50, 70-80,
Vpl.
Against this background, an interval of "disturbed cyclicity" of
Vpl and high
dVpl values is clearly observed in the Vendian-uppermost
Riphean (650-530 Ma). Based on
direct measurements of intervals between adjacent maximums (minimums)
and wavelet analysis results (D. K. Galyagin and P. G. Frik),
the following characteristic times are recognized in the cyclicity of
Vpl,
dVpl,
VD, and
dVD : 20-30, 40-50, 70-80,
 100,
and
100,
and
 130 Myr.
130 Myr.
Comparison Between Continental Plate Velocities and Geomagnetic
Reversal Frequency in the Neogaea
First, I compare kinks in the plate APWPs with field reversal
frequency
(F) extremums (Figures 1a and 1b).
As seen from Table 2, 14 kinks coincide with minimums of
F,
six coincide with its maximums, and four are
behind
Fmin by 20-40 Myr; i.e., similar to biota variations,
sharp changes in the paleomagnetic pole
position are mostly synchronous with reversal frequency extremums,
although there are more complex cases of
delayed variations.
 Now I compare the maximums (minimums) of
Vpl,
dVpl,
VD, and
dVD with the closest
reversal frequency maximums (minimums) of the field
Fm.
Unlike similar comparison with variation
rates of the organic world (see above), a scatter of the extremums is broader
(Figure 12),
which may be related
to various uncertainties. The differences
Vm-Fm and
dVm-Fm mostly form two groups: they are either
close to
zero ( 0
Now I compare the maximums (minimums) of
Vpl,
dVpl,
VD, and
dVD with the closest
reversal frequency maximums (minimums) of the field
Fm.
Unlike similar comparison with variation
rates of the organic world (see above), a scatter of the extremums is broader
(Figure 12),
which may be related
to various uncertainties. The differences
Vm-Fm and
dVm-Fm mostly form two groups: they are either
close to
zero ( 0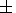 20 Myr) or negative (mainly in the interval
of
-30 to
-60 Myr);
therefore, the velocity extremums
and their scatter are either synchronous with the reversal
frequency extremums or behind those by the value
close to delay times of geological era onsets with respect to reversal
frequency minimums (Figure 1a).
In spite of a large scatter, alternation of intervals dominated by
minimum differences
Vm-Fm
20 Myr) or negative (mainly in the interval
of
-30 to
-60 Myr);
therefore, the velocity extremums
and their scatter are either synchronous with the reversal
frequency extremums or behind those by the value
close to delay times of geological era onsets with respect to reversal
frequency minimums (Figure 1a).
In spite of a large scatter, alternation of intervals dominated by
minimum differences
Vm-Fm 0
and those with the prevailing values
Vm-Fm
0
and those with the prevailing values
Vm-Fm -40
-40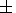 20 Myr is evident
(Figure 13).
The characteristic time of this alternation is
350-400 Myr.
20 Myr is evident
(Figure 13).
The characteristic time of this alternation is
350-400 Myr.

The above data may be interpreted as evidence of two active mechanisms:
the outer, operating synchronously
at the core and Earth's surface, and inner, responsible for the values
Vm- Fm = -40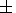 20 Myr. Negative
values of
Vm- Fm are a result of the energy transfer
from the core-mantle boundary (D''
layer) to the surface
(plumes, mantle convection, and so on). A delay of
-40
20 Myr. Negative
values of
Vm- Fm are a result of the energy transfer
from the core-mantle boundary (D''
layer) to the surface
(plumes, mantle convection, and so on). A delay of
-40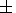 20 Myr
indicates the velocity of the energy transfer
to be 5-10 cm/yr. Such a velocity is consistent with Figure 8
and known estimates of mean velocities of major plates
[Jurdy et al., 1995;
Zonenshain et al., 1987, 1990].
20 Myr
indicates the velocity of the energy transfer
to be 5-10 cm/yr. Such a velocity is consistent with Figure 8
and known estimates of mean velocities of major plates
[Jurdy et al., 1995;
Zonenshain et al., 1987, 1990].
 The mechanisms may be further specified from the correlation between
Vpl and
Vm- Fm. If the inner
mechanism is dominated by convective motions in the mantle,
these values should be inversely correlated,
whereas the plume mode of energy transfer probably implies such
a correlation to be absent, because
continental plate motions are nearly independent of the plume ascent,
but they are significantly affected by
convective motions in the upper mantle; no correlation should
exist in the case of operation of the external
mechanism. The values of
Vpl and
Vm- Fm are likely to
be uncorrelated in both intervals
0
The mechanisms may be further specified from the correlation between
Vpl and
Vm- Fm. If the inner
mechanism is dominated by convective motions in the mantle,
these values should be inversely correlated,
whereas the plume mode of energy transfer probably implies such
a correlation to be absent, because
continental plate motions are nearly independent of the plume ascent,
but they are significantly affected by
convective motions in the upper mantle; no correlation should
exist in the case of operation of the external
mechanism. The values of
Vpl and
Vm- Fm are likely to
be uncorrelated in both intervals
0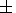 20 Myr and
-40
20 Myr and
-40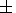 20 Myr (an inverse correlation seems to
exist in the
case of minimum values of
Vpl, see Figure 14).
Whereas the absence of correlation in a
0
20 Myr (an inverse correlation seems to
exist in the
case of minimum values of
Vpl, see Figure 14).
Whereas the absence of correlation in a
0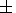 20-Myr interval supports
the action of the external
mechanism, the absence of correlation in the second interval implies
that the mantle convection is uninvolved
in the interrelation between the processes in the core and lowermost mantle
(D''
layer) and movements in the
lithosphere. This may be explained by the fact that processes in the
D''
layer and mantle convection are
independent, as is indicated, for example, immobility of hotspots relative
to moving plates (which is used for
estimation of absolute plate movements)
[Jurdy et al., 1995;
Zonenshain et al., 1987].
The correlation may be
disturbed by two-layer convection (in upper and lower mantle)
which accounts for not more than 10% heat and mass transfer
[Allegre, 1997].
20-Myr interval supports
the action of the external
mechanism, the absence of correlation in the second interval implies
that the mantle convection is uninvolved
in the interrelation between the processes in the core and lowermost mantle
(D''
layer) and movements in the
lithosphere. This may be explained by the fact that processes in the
D''
layer and mantle convection are
independent, as is indicated, for example, immobility of hotspots relative
to moving plates (which is used for
estimation of absolute plate movements)
[Jurdy et al., 1995;
Zonenshain et al., 1987].
The correlation may be
disturbed by two-layer convection (in upper and lower mantle)
which accounts for not more than 10% heat and mass transfer
[Allegre, 1997].
As seen from Figures 13 and 14, the variation ranges of mean plate
velocities in both mechanisms are very
close (10-60 and 20-55 km/Myr) and overlap the range of possible
dependence of
Vpl on
Vm- Fm.
Therefore, the variations in the
Vpl means are caused by
general factors that affect both external and
internal mechanisms. The rate of core-to-surface energy transfer varies
within comparatively narrow limits as
is evident from a
-40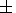 20-Myr range of delay times between
velocity and reversal frequency extremums and
from overlapping ranges of variation in maximum and minimum values
of mean velocities of paleolatitude
plate movements (these ranges are, respectively, 30-60 and 10-45 km/Myr
for the external mechanism and
40-55 and 20-40 km/Myr for the internal one (Figure 14).
Thus, irrespective of geomagnetic field generation
mechanisms and plate movements, the rates of core-to-surface energy
transfer and plate motions are close,
which is evidently due to properties of the medium. As seen from Figure 13,
there exist time intervals
dominated by the action of the external synchronous mechanism
( Vm- Fm=0
20-Myr range of delay times between
velocity and reversal frequency extremums and
from overlapping ranges of variation in maximum and minimum values
of mean velocities of paleolatitude
plate movements (these ranges are, respectively, 30-60 and 10-45 km/Myr
for the external mechanism and
40-55 and 20-40 km/Myr for the internal one (Figure 14).
Thus, irrespective of geomagnetic field generation
mechanisms and plate movements, the rates of core-to-surface energy
transfer and plate motions are close,
which is evidently due to properties of the medium. As seen from Figure 13,
there exist time intervals
dominated by the action of the external synchronous mechanism
( Vm- Fm=0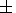 20 Myr)
or internal
mechanism with a characteristic delay time of
-40
20 Myr)
or internal
mechanism with a characteristic delay time of
-40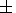 20 Myr.
In particular, the aforementioned Vendian
interval with "anomalous"
Vpl and
dVpl lies within the longest interval dominated by the action of
the external mechanism (Figures 1 and 13).
20 Myr.
In particular, the aforementioned Vendian
interval with "anomalous"
Vpl and
dVpl lies within the longest interval dominated by the action of
the external mechanism (Figures 1 and 13).
Generalization of results
The above data imply that the relations between processes in
the core and lowermost mantle on the one hand
and at the Earth's surface on the other hand are realized at least at
three time scale levels.
First time scale level
is the whole Neogaea.
At the Earth's surface, a relevant characteristic feature is a
different degree of differentiation of the chronostratigraphic scale
in the Riphean and Vendian-Phanerozoic
(Figure 8),
which is evidence of an intense rise in the development of
various life forms that began in the
Vendian-Cambrian. The final interval of the Riphean-Vendian (650-530 Ma)
is characterized by disturbed
cyclicity of the continental plate velocity
(Vpl) variation (Figure 10), and the Vendian interval of
anomalous
Vpl lies within the longest interval dominated
by action of the external mechanism (Figures 1
and 13). The conclusive stage of existence of the Riphean supercontinent
Pangea and its breakup also took
place at that time. The peak of tectonic and thermal activity,
lying approximately between 570 and 500 Ma,
was associated with a higher heat flow, the widest occurrence of
the granulite facies of metamorphism,
reworking of the crust, and epeirogenic uplifts and basalt
outflows
possibly related to mantle plumes
[Williams, 1994].
At the same time, essential changes at the core-mantle boundary
markedly affected all
characteristics of the geomagnetic field, particularly,
its reversal frequency whose pattern is very close to the
"frequency" of startigraphic stages (Figure 8).
The geomagnetic field behavior differs in its fractality. A
difference between the Riphean and Phanerozoic intervals and uniqueness
of their boundary which manifested
themselves at both the Earth's surface and core may be explained
by resonance-type enhancement of core
motions, caused by critical duration of the Earth's diurnal rotation
(  22.2 hours) due to the tidal decrease in
its angular velocity by a factor of about 1.5 from the Archean to present time.
This deceleration resulted in a
considerable temperature increase near the core-mantle boundary,
destabilization of the D''
layer, and ascent of mantle plumes
[Williams, 1994].
22.2 hours) due to the tidal decrease in
its angular velocity by a factor of about 1.5 from the Archean to present time.
This deceleration resulted in a
considerable temperature increase near the core-mantle boundary,
destabilization of the D''
layer, and ascent of mantle plumes
[Williams, 1994].
Second level
is the scale of geological eras,
characterized by their onset delay with respect to reversal
frequency minimums throughout the Neogaea. On this scale,
long intervals of stable geomagnetic polarity,
typically preceding the beginning of geological eras occur cyclically with
a 160-200-Myr period close to the
era duration (except for two anomalies between 1150 and 1100 Ma
and between 700 and 630 Ma). This
regularity is supported by a fractal dimension of reversal frequency
of about 0.9 in the Neogaea. These stable
polarity intervals are likely to coincide with plate velocity minimums,
which is natural, given stable conditions
at the core and Earth's surface. The aforementioned delay amounts to 35-60 Myr
(Figure 1)
and yields a value
of 4-10 cm/yr for the energy transfer rate from the core-mantle
boundary to the Earth's surface, i.e., for the
mantle convection velocity. This value is consistent with mean velocity
estimates for the drift of major
continental plates (Figure 10)
[Jurdy et al., 1995;
Zonenshain et al., 1987].
Therefore, boundaries of
geological eras are mainly related to the action of inner mechanism.
Third level
is the scale of geological periods.
First, it is characterized by nearly exact coincidence of
minimums or maximums; i.e., variations in the organic world and
continental plate velocities occur
synchronously with the polarity reversal frequency and variations
in the geomagnetic paleointensity (Figures 1, 8, and 10).
Moreover, geomagnetic events are synchronous with such "lithospheric"
events as trap outflows,
jumps in the spreading velocity, stratigraphic unconformities
in geological sections (reflecting fluctuations in
the sea level), folding phases, appearance of evaporites and tillites
(climatic changes), occurrence of black
shales (redox conditions). Most prominent is the coincidence
of the above events at times of 250-245, 196-190, 148-144, 113-110,
and 97-91 Ma
[Rampino, 1988;
Rampino and Caldeira, 1993;
also see Introduction].
The cyclicity of all aforementioned processes exhibits periods ranging from
20 to 100 Myr (periods of ~20-30, ~50, and ~100
are best defined). In addition, many boundaries of geological
periods coincide with
narrow minimums less than 10 Myr long and small kinks in the
reversal frequency and/or paleointensity
variations (Figure 1). Consequently, accelerations or decelerations
core-mantle boundary processes, variations
in the organic world, plate motions, and other processes at the Earth's
surface occur synchronously, and
boundaries of geological periods are often associated with a decrease
in the reversal frequency and
geomagnetic paleointensity and often manifest a decline in the organic
world development (Figures 1 and 8).
Second, in addition to synchronism (coincidence of
Vm and
Fm extremums),
Vm extremums
are behind the reversal frequency extremums mainly by 30-60 Myr.
A similar delay is observed in the onsets
of geological eras with respect to reversal frequency minimums
(Figures 1
and 13).
Moreover, intervals
dominated by the differences
Vm- Fm=0 alternate with those dominated by
Vm- Fm=40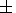 20 Myr
(Figure 13).
The characteristic time of their alternation is 350-400 Myr,
which is a twofold cyclicity period of
constant polarity intervals.
20 Myr
(Figure 13).
The characteristic time of their alternation is 350-400 Myr,
which is a twofold cyclicity period of
constant polarity intervals.
These data may be explained in terms of active mechanisms
of two types:
an external mechanism that acts
synchronously at the core and Earth's surface and an internal mechanism
responsible for a
-40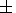 20-Myr delay
of processes at the Earth's surface with respect to those at the core.
In all of the cases, this is only a qualitative
relationship, whereas no numerical relation between processes at
the surface and core virtually exists (Figures 9 and 14).
Consequently, there is no causal connection between these processes; rather,
they are subjected to the action of a general mechanism.
20-Myr delay
of processes at the Earth's surface with respect to those at the core.
In all of the cases, this is only a qualitative
relationship, whereas no numerical relation between processes at
the surface and core virtually exists (Figures 9 and 14).
Consequently, there is no causal connection between these processes; rather,
they are subjected to the action of a general mechanism.
The aim of this paper is to constrain current hypotheses using
available information rather than to determine a
specific mechanism (or mechanisms).
On the one hand, there exist processes that are useful for reasonable
explanation of synchronism of events at
the Earth's surface and core such as the tidal evolution of the Earth-Moon
system, evolution of the Earth as a
part of the Solar system, and general evolution of the Galaxy.
Thus, tidal movements produce periodic
variations in the angular velocity of the Earth, Earth-Moon distance,
and inclination of the rotation axis; as a
result, the rotation poles of the Earth markedly change their position
(rotations of the planet as a whole
relative to the ecliptic and/or rotations of the mantle relative to the core).
The same group of processes
includes changes in the rotation axis position caused by the
continental drift. The above phenomena in turn
lead to changes in climate, sea level, and position of the core,
which should affect the geomagnetic field. Thus
deceleration-acceleration regimes of the Earth's rotation should result
in polarity reversals or preferred
polarity intervals. Furthermore, the intervals of maximum gradients
in mean velocities of the continental drift,
summary amplitude extremums of direction paleovariations, and maximums
of prevailing reversed polarity
are very close to the epochs of the Solar system passage through
the Galaxy plane; the main period of such
oscillations is close to 30 Myr and virtually coincides with
the main period of fauna extinctions, sea level
lowering, large basalt outflows, folding, abrupt drops in spreading rate,
and enhancement episodes of
reduction conditions over the past 250 Myr
[Rampino, 1988;
Rampino and Caldeira, 1993],
but it is also the
half-period of variations in main parameters of the geomagnetic
field in the Neogaea; finally, one of the
periods of field characteristics and plate motions, considered above,
is close to the Galactic year.
On the other hand, there are surface processes
(geological era onsets, variations in mean velocities of
continental plate motion, etc.) that proceed later than those
at the core-mantle boundary (Figure 13); this delay
is most naturally treated in terms of the energy transfer from
the core-mantle boundary (D''
layer) to the
Earth's surface (plumes, mantle convection, etc.).
The delay time constraint provides a value of 5-10 cm/yr for
the energy transfer rate, which is consistent with velocities
of major plates. Lacking (or very weak) numerical
correlation implies that the mantle convection cannot be responsible
for the interrelation between processes in
the D''
layer and lithospheric motions.
This may be explained in terms of two-layer convection (in the lower
and upper mantle) with very limited heat and mass transfer
between these layers (not more than 10%)
[Allegre, 1997]
and/or by the fact that processes in the D''
layer and mantle are independent.
General action of the two mechanisms may be described as follows.
The external mechanism causes processes
in the D''
layer (activity, instability, etc.)
which stimulate the heat and mass transfer in the mantle, i.e., bring
about the action of internal mechanism. Furthermore, mantle mass
movements (convection, plumes,
subduction), caused by the activity in the D''
layer and related
to plate motions, change the planetary moment
of inertia, i.e., bring about synchronous action of the external
mechanism, and so on. Such a relation is
supported by very close limits of variations in mean velocities
of plate motion as constrained by each of the
mechanisms (10-60 and 20-55 km/Myr, respectively).
In general, irrespective of mechanisms responsible for the geomagnetic
field generation and plate movements,
the energy transfer from the core to Earth's surface and plate
movements have close velocities, so that these
processes are evidently controlled by properties of the medium.
This document was generated by TeXWeb
(Win32, v.1.0) on April 7, 1999.
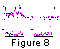 To compare the geomagnetic field behavior with changes in
the organic world,
I used (1) changes in the
number of units in the chronostratigraphic scale (Figure 8a),
(2) changes in the diversity of families of marine
organisms, and (3) extinctions of marine organism families that occurred every
10 Myr (Figure 8c). The
chronostratigraphic scale of Harland et al. [1990]
with certain modifications (see Part 1) was used for the
discussion of topic (1), and topics (2) and (3) will be discussed on
the basis of the Phanerozoic summary
presented by Benton [1995] (unfortunately, data on
the Riphean are not so representative); only the data on
marine organisms were used because they are more representative of the whole
Phanerozoic. All data are
correlated with the general geological time scale.
To compare the geomagnetic field behavior with changes in
the organic world,
I used (1) changes in the
number of units in the chronostratigraphic scale (Figure 8a),
(2) changes in the diversity of families of marine
organisms, and (3) extinctions of marine organism families that occurred every
10 Myr (Figure 8c). The
chronostratigraphic scale of Harland et al. [1990]
with certain modifications (see Part 1) was used for the
discussion of topic (1), and topics (2) and (3) will be discussed on
the basis of the Phanerozoic summary
presented by Benton [1995] (unfortunately, data on
the Riphean are not so representative); only the data on
marine organisms were used because they are more representative of the whole
Phanerozoic. All data are
correlated with the general geological time scale.
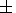 10 Myr, which yields 4-10 cm/yr for
the energy transfer rate from the core-mantle boundary to surface, i.e.,
for the mantle convection velocity.
This value agrees with average velocities estimated for the drift of
main continental plates (see below)
[Jurdy et al.,
10 Myr, which yields 4-10 cm/yr for
the energy transfer rate from the core-mantle boundary to surface, i.e.,
for the mantle convection velocity.
This value agrees with average velocities estimated for the drift of
main continental plates (see below)
[Jurdy et al., 


 Vpl.
Against this background, an interval of "disturbed cyclicity" of
Vpl and high
dVpl values is clearly observed in the Vendian-uppermost
Riphean (650-530 Ma). Based on
direct measurements of intervals between adjacent maximums (minimums)
and wavelet analysis results (D. K. Galyagin and P. G. Frik),
the following characteristic times are recognized in the cyclicity of
Vpl,
dVpl,
VD, and
dVD : 20-30, 40-50, 70-80,
Vpl.
Against this background, an interval of "disturbed cyclicity" of
Vpl and high
dVpl values is clearly observed in the Vendian-uppermost
Riphean (650-530 Ma). Based on
direct measurements of intervals between adjacent maximums (minimums)
and wavelet analysis results (D. K. Galyagin and P. G. Frik),
the following characteristic times are recognized in the cyclicity of
Vpl,
dVpl,
VD, and
dVD : 20-30, 40-50, 70-80,
 100,
and
100,
and


