The geomagnetic polarity time scale underlies the analysis
of such paleomagnetic field characteristics as
reversal frequency (Figure 1a) and polarity bias (Figure 1c).
All surface phenomena of the Earth, including geomagnetic field characteristics, are referred, one way or another, to time ("dated"). Radiometric datings bear a global character, but even they "change" with time, because decay constants are refined, new methods appear and old ones are improved, and so on. Biostratigraphic datings are less reliable and are often reasonable only on a regional scale. They need be correlated with the general geochronological scale. However, time and again this scale is improved, and paleomagnetic data obtained at various times are time correlated with somewhat different geochronological scales. Therefore, it is important to choose the scale that fixes dates for the greater part of the available information, and the remaining data should be correlated with this scale. This is the geochronological scale of Harland et al. [1990], with the following corrections introduced into position of boundaries in the Cambrian and Vendian [Grotzinger et al., 1995] and in the Riphean [Semikhatov and Raaben, 1996]: Tremadocian, 505 Ma; Upper Cambrian (divided into two equal intervals), 510 Ma; Middle Cambrian (divided into two equal intervals), 520 Ma; Bothomian, 525 Ma; Atdabanian, 528 Ma; Tommotian, 530 Ma; Rovenskii horizon (Nemakitian-Daldynian), 544 Ma; Kotlinskian, 551 Ma; Redkinskian, 570 Ma; Laplandian (Varanger), 610 Ma; Upper Riphean, 1050 Ma (divide into two intervals at 850 Ma); Middle Riphean, 1350 Ma (divided into two intervals at 1200 Ma); and Lower Riphean, 1650 Ma (divided into two intervals at 1450 Ma).
Of course, the scheme offered is open to criticism, but the dating accuracy of each boundary is not as important for our analysis as the correlation of the whole body of information, both paleomagnetic and geological, with one geochronological scale. (Dating uncertainties are largely reduced through smoothing.)
A composite time scale of geomagnetic polarity (Table 1) was constructed to study the polarity behavior in the Neogaea.
(1) The scale of Harland et al. [1990] was taken for times younger than 170 Ma. (2) The magnetostratigraphic scale constructed for the USSR territory was accepted as a basis for the Paleozoic and Mesozoic time [Khramov et al., 1982; Molostovsky and Khramov, 1984]. It was improved and complemented by the following regional magnetostratigraphic scales: (a) Upper Triassic-Lower Jurassic of the Newark basin [Witte et al., 1991]; (b) Carboniferous of North America [Opdyke and Divenere, 1995]; (c) Lower Carboniferous-Upper Cambrian of Ural [Danukalov et al., 1983]; (d) composite magnetostratigraphic scale of the Lower and Middle Ordovician [Trench et al., 1991]; (e) Ordovician-Upper Cambrian of Siberia [Gallet and Pavlov, 1996, 1999; Pavlov and Gallet, 1998]; (f) Lower Cambrian of East Siberia [Kirschvink and Rozanov, 1984]. (3) The following data were used for the Vendian and Riphean: (a) composite magnetostratigraphic scales of the Vendian-Riphean of Kuznetskii Alatau, East Siberia [Osipova et al., 1988] and mid-Proterozoic supergroup, Montana and Idaho, North America [Elston and Bressler, 1980]; these scales are intercorrelated both generally and in the number of reversals; (b) Vendian section of the Pridnestrov'e area [Tretyak et al., 1996]; (c) part of the Upper Riphean Katav Formation section, South Ural [Komissarova et al., 1997]; (d) Mamainse Point volcanics section (Keweenawan record, Middle Riphean, 1109 to 1086 Ma) [Klewin and Berg, 1990]; (e) magnetostratigraphic section of Lower Riphean deposits, McArthur basin, Australia [Idnurm, 1992].
Younger scale intervals are naturally more reliable than older ones. Magnetostratigraphic data, obtained both before and after 1980, often do not meet the modern standard requirements of paleomagnetic reliability. There are works in which only the boundary ages of formations and other large units are reported, whereas boundary ages of magnetic zones are estimated approximately, in proportion to section thickness. For example, such an approach was applied to age determinations of magnetic zone boundaries in sections of the Katav Formation, Lower Cambrian of Siberia, Mamainse Point, Lower Riphean deposits in the McArthur basin, and others. Some regional scales have gaps and undifferentiated intervals of frequent polarity reversals. Gaps in the scales caused by lacking data were treated as follows: if magnetic polarities at the ends of an undocumented interval are opposite, the boundary between magnetic zones is fixed at midpoint of the interval, and if the ends have the same polarity, it was assigned to the whole interval. Undifferentiated intervals of frequent polarity reversals, recognized in the Paleozoic, were treated by the following procedure. As will be shown below, the majority of short magnetic zones in the Mesozoic and Late Paleozoic are longer than 0.25 Myr, and the undifferentiated intervals were "filled" with uniformly alternating zones of normal and reversed polarities at a frequency of 2-4 reversals per 1 Myr. The composite scale was brought into correspondence with the geochronological scale (see above).
Of course, the geomagnetic polarity time scale constructed in this way (Table 1) is not free from drawbacks and is unsuitable for accurate age correlation and other magnetostratigraphic problems; moreover, it may be incomplete, particularly in the Precambrian. However, this work primarily addresses global statistical properties of the scale in order to reveal large-scale regularities and peculiarities in the geomagnetic field behavior, as well as to correlate those with other large-scale phenomena of the Earth.
I emphasize that the geomagnetic polarity time scale cannot be significantly extended into the past, because only episodically there are found rocks older than 2.0 Ga that form continuous stratigraphic sequences unaffected by significant alterations over their geological history and preserve initial paleomagnetic record.
The geomagnetic polarity time scale underlies the analysis
of such paleomagnetic field characteristics as
reversal frequency (Figure 1a) and polarity bias (Figure 1c).
To assess the reliability of the polarity time scale and related reversal pattern, relative polarity sign changes were estimated with the help of other method [McElhinny, 1971], namely from the percentage of individual paleomagnetic determinations (collections) including both field polarities with respect to their total number in a given time interval (in our case, 10 Myr, Figure 1b). This method requires statistically representative data and even in this case its results are essentially of comparative merit. In applying this method, I used the paleomagnetic database created by McElhinny and Lock [1990, 1993] and compared results with the curve constructed by the same method for the most of Phanerozoic [Johnson et al., 1995]. Both curves, based on somewhat different approaches to the choice of data, virtually coincided. The Riphean section is less reliable due to long intervals for which the number of paleomagnetic determinations is less than five or they are unavailable at all.
The geomagnetic field sign patterns obtained for the Phanerozoic and Vendian by two essentially independent methods are qualitatively very similar, thereby confirming the reliability of the polarity variation (cyclicity) pattern, at least in the Phanerozoic and Vendian. Application of the two methods to the Riphean yielded differing results, which indicates the Riphean reversal pattern and Riphean interval of the polarity time scale to be incomplete [Pechersky, 1997]. For example, marked increases in the reversal frequency obtained for the intervals 750-850 Ma, near 950 Ma, and others (Figure 1b) are not matched by a noticeable increase in the field reversal frequency in the polarity time scale (Figure 1a).
The above similarity between reversal frequency variations obtained by different methods is unrelated to their amplitudes: even in the most reliable, Cenozoic-Late Paleozoic interval of the scale (Figure 1a), the peak-to-valley value of the field reversal frequency variations as determined by the second method (Figure 1b) is several times higher than the actual value. However, their synchronism and cyclicity in the Phanerozoic-Vendian allow one to expect that the Riphean data are, on the whole, also reliable.
As is evident from Table 1 and Figure 1, geomagnetic polarity patterns in the Phanerozoic and Precambrian are strongly different: Phanerozoic reversals were more frequent than Precambrian ones; moreover, a general increase in the number of reversals is observed: on average, one reversal occurs every 15.6 Myr in the Riphean, 1.7 Myr in the Paleozoic, 1.2 Myr in the Mesozoic, and 0.35 Myr in the Cenozoic, with long intervals of constant magnetic polarity being rather uniformly distributed throughout the Neogaea.
Whereas the symmetry of magnetic hydrodynamics equations implies both polarities of the geomagnetic field to be equiprobable, intervals of dominating, normal or reversed, polarity are actually observed (Figure 1c). Importantly, the Phanerozoic polarity asymmetry derived from the geomagnetic polarity time scale coincides with the statistical estimate of the bias obtained from paleomagnetic directions of each collection included in the paleomagnetic database [Algeo, 1996], thereby confirming the reliability of the Phanerozoic polarity bias. Unfortunately, the second method fails to specify the polarity asymmetry in the Riphean, because polarity determinations are lacking for many database entries [McElhinny and Lock, 1990, 1993].
The observed complicated behavior of the polarity asymmetry cannot be explained within the framework of current dynamo models. Apparently, its origin should be sought for not in the core but in the mantle, its interaction with the core, and in external sources that change geomagnetic field generation conditions.
Histograms of magnetic zone durations (Figure 2) are
generally similar for various time intervals.
First, each histogram has a single mode and is close to a
lognormal distribution, which indicates representativity of the Phanerozoic and Precambrian
scales. Second,
lengths of magnetic zones gradually increase with age,
from 0.1-0.2 Myr in the Anthropogene-Miocene
(Figure 2a)
to 0.5-1 Myr in the time interval from the Early Mesozoic-Late
Paleozoic (Figure 2d,
e) through
the earliest Riphean (Figure 2g). Therefore, magnetic zones are mostly
0.2-2.5 Myr long throughout the
Neogaea and, beginning from the Late Mesozoic, gradually decreases
to 0.1-0.5 Myr. This fact cannot be
accounted for by systematic errors, because the mode is mostly displaced within the
scale interval constructed
by one method, mainly from linear magnetic anomalies in oceans (Figures 2a-2c).
Third, numerous data
[Petrova, 1989;
Petrova and Pospelova, 1990;
Petrova et al., 1992]
indicate the presence of very short episodes
of opposite polarities and excursions not included in the scales used for the construction
of the composite
Neogaean scale. For example, the Brunhes subchron includes at least ten of such excursions.
Thus, many tens
of magnetic zones that are shorter than 0.01 Myr may exist; they form a separate
set and have other origin.
Fourth, the right-hand "tails" of the histograms disappear in the interval from the
Riphean to Cenozoic
(Figure 2): the percentage of zones longer than 5 Myr is 35%
in Riphean, 6% in Paleozoic, and 2.6% in Late
Mesozoic; in Cenozoic those are absent. Fifth, the Neogaea includes intervals dominated
by one
polarity as long as tens of millions of years (superchrons and hyperchrons
according to magnetostratigraphic classification [Khramov et al., 1982;
Molostovsky and Khramov, 1984;
Molostovsky et al., 1976;
Pechersky, 1985]).
They are "centered" at rather regularly distributed moments
of
1680, 1520, 1360, 1150, 1100, 900,
700, 630, 470, 290, and
100 Ma spaced by about 160-200 Myr
with the exception of two anomalies
between 1150 and 1100 Ma and between 700 and 630 Ma (Figure 1a, b).
Thus, in view of data on excursions and short episodes, at least three field generation modes are conceivable. Fractal analysis of the scale [Pechersky et al., 1997] substantiates reliability of the above pattern (see below).
The case study of the geomagnetic polarity time scale over the past 170 Myr showed that the reversal sequence is aperiodic (in the strict sense of this term) and random and have fractal properties [Ermushev et al., 1992; Gaffin, 1989; Ivanov, 1996; Merrill and McElhinny, 1983].
Presently, numerical modeling methods applied to the fractal sequence of geomagnetic reversals yield rather divergent results. There are models that give periodic or quasi-periodic solutions; on the other hand, Anufriev and Sokoloff [1994] obtained reversal sequences with fractal properties consistent with observations. The long Neogaean scale allows a more detailed examination of its fractal properties [Pechersky et al., 1997].
A characteristic feature of the Neogaean scale is the presence of constant polarity intervals whose lengths differ by more than two orders of magnitude (Table 1), which implies possible similarity between various time scales (fractality).
To study fractal properties of a geomagnetic polarity scale of length T, let N be the number of time intervals of length D which contain at least one reversal of the scale. The log-log dependence of ln N versus lnD is a linear function whose slope is the fractal dimension d. Time series that have a constant dimension from the interval 0.5<d<1 over the time period under consideration are fractal, i.e. they possess the self-similarity property.
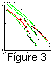Two linear intervals with
d1 0.5 and
d2 0.87 are recognized in
the interval 170-0 Ma, with the
slope of the function
N(D) changing at about 2 Myr
[Ivanov, 1996]. For the intervals 250-0 Ma
(Cenozoic-Mesozoic, the scale is nearly as reliable as in the previous
interval) and 560-0 Ma (Phanerozoic), the fractal
characteristics remain almost the same:
d1 0.55 and
d2 0.83,
and the kink is displaced toward
greater
D (Figure 3)
[Pechersky et al., 1997].
Finally, if the interval 1700-0 Ma is considered, a
second kink at
D of about 50 Myr appears, and three linear
segments are recognized with
d1 0.55,
d2 0.66,
and
d3 0.87. The second kink of
the function
N(D) may be due to either (a) the fact
that the Precambrian scale interval
is less studied or (b) the presence of a physical process having a
different fractal dimension. The following test
[Pechersky et al., 1997] was performed to verify the
first
hypothesis: all Neogaean intervals with
D< 1 Myr
were rejected (about 20% of reversals remained),
but this did not affect the position of the kink within the 1700-0 Ma
interval ( d1 0.52 and
d2 0.88 ).
Since missing reversals in the Precambrian interval of the Neogaean
scale are unlikely to exceed 80%,
they cannot be responsible for the second kink in
N(D).
To verify the second hypothesis, relatively uniform intervals
with minimum reversal frequency (1600-445, 370-170, and 125-73 Ma)
were chosen. Then, the remaining intervals are characterized by higher reversal
frequencies, and fractal analysis was applied separately to each
of the two sets. I should emphasized that each
group included intervals from both the Cenozoic-Mesozoic and less reliable
Early Paleozoic-Precambrian
segments of the scale. Analysis of the first set yielded the
N(D) kink at the same place as in the 1700-0 Ma
variant (Figure 3)
and the same dimensions of the sets
d1 0.56 and
d2 0.86. Consequently, there
are no reasons to associate the fractal set with
d<0.6 only with high reversal frequency intervals. The
second case gave a pattern very close to the 170-0 Ma variant,
with
d1 0.56 and
d2 0.9 (Figure 3).
Thus, there exist three modes of the geomagnetic field generation reflected
in three fractal dimensions of the
reversal scale. In other words, the Neogaean scale represents superposition
of three processes with fractal
dimensions
d1 0.56,
d2 0.66, and
d3 0.87. The first is nearly
chaotic, and the third results
in concentrations (clusterization) of polarity reversals with appearance of
long intervals of rare reversals; in
the scale, this is reflected by regularly alternating superzones
of frequent reversals (unstable field) and
constant polarity (stable field). Moreover, patterns with different
dimensions are superimposed, and the
d2 0.66 pattern may be a
result of such a superposition.
This is confirmed by the sample dependence of
kink positions and by the fact that a gradual increase in the starting
time moment does not produce in abrupt
transitions between the curves
N(D) but results in their smooth deformation
associated with the lengthening
of the series
[Pechersky et al., 1997].
Any interpretation of fractal analysis results
[Anufriev and Sokoloff, 1994;
Ivanov, 1996;
Pechersky et al., 1997]
indicates the geomagnetic reversal sequence to be fractal, with a
dimension
d of about 0.5-0.6 and 0.9, which is conformable
to the observed alternation of high reversal
frequency intervals with rather long intervals of rare reversals
and to chaotic distribution of reversals spaced
by less than 2-3 Myr
[Cox, 1981].
These regularities are observed against the background of a general
increase in the reversal frequency from the Early Riphean to Late
Cenozoic, with cyclicity of long intervals of
constant polarity being on the whole preserved.