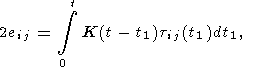
B. I. Birger
Schmidt United Institute of Physics of the Earth, Russian Academy of Sciences, Bol'shaya Gruzinskaya ul. 10, Moscow, 123810 Russia
A power-law non-Newtonian fluid is usually assumed to model slow flows in the mantle and, in particular, convective flows. However,the power-law fluid has no memory in contrast to a real material. A new nonlinear model with a memory was recently proposed recently by Birger [1998]. The proposed model reduces to the power-law fluid model for stationary flows and to the Andrade model for flows associated with small strains.
The steady-state convection beneath continents was studied by Fleitout and Yuen [1984], who used a power-law fluid model and obtained a cold immobile boundary layer (the continental lithosphere). In stability analysis of this layer, the Andrade model must, however, be used. The analysis shows that the lithosphere is overstable, with a period of oscillations of about 200 Ma. These thermoconvective oscillations of the lithosphere are suggested to provide a mechanism for the formation and evolution of sedimentary basins on continental cratons [Birger, 1998]. The vertical crustal movement in sedimentary basins can be respresented as a slow subsidence on which small-amplitude oscillations are superimposed. The longest period of the oscillatory crustal movement is of the same order of magnitude as the period of convective oscillation of the lithosphere found in the stability analysis. Taking into account the difference between the depositional and erosional transport rates we can explain the permanent subsidence of sedimentary basins, as well as their oscillation [Birger, 1998].
Analysis of convective stability for a horizontal layer involves perturbations harmonically depending of the horizontal coordinate. For a layer with the Andrade rheology, the instability is oscillatory and perturbations can take the form of travelling and standing thermoconvective waves. In this study, we adress the problems on the generation of thermoconvective waves under various initial conditions: the linearized equations for thermal convection in a layer with the Andrade rheology are solved for given initial perturbations of temperature.
A linear rheological model (having a memory) of the lithosphere is described by the integral relationship
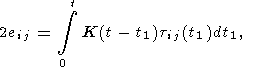 | (1) |
where eij and tij are the deviatoric strain and stress tensors, respectively, t is time, and K(t) is the creep kernel given by
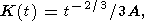 | (2) |
where A is the Andrade rheological parameter. The creep kernel (2) is introduced so that, in the case of constant stress, the strain depends on time as t1/3 (the Andrade law).
The linearized equations of thermal convection in a horizontal layer heated from below are written as
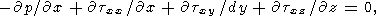 |
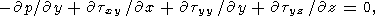 |
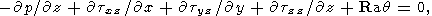 | (3) |
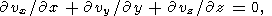 |
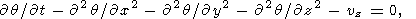 |
where z is the vertical coordinate, x and y are the horizontal coordinates, v is the velocity, q and p are the perturbations of temperature and pressure. The set of equations (3) is written in the dimensionless form. The length scale is layer thickness d and the temperature scale is a temperature drop DT between the hot lower and cold upper surfaces of the layer (both surfaces are supposed to be isothermal). The time scale is d2/k, where k is the thermal diffusivity, and the velocity scale is k/d. For a Newtonian fluid, the stress (and pressure) scale khd2 is usually taken, and the Rayleigh number is Ra = rgaDTd3/hk, where r is the density, a is the thermal expansion coefficient, g is the gravitational acceleration, and h is the Newtonian viscosity having the dimension of Pa s. For the Andrade rheological medium (the Andrade parameter A has the dimension of Pa s 1/3 ), we introduce a reference viscosity
Then, the Rayleigh number is defined as
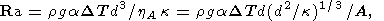 | (4) |
and the stress scale is khA d2 = A(d2/k)-1/3.
The lithosphere is characterized by the following depth-averaged values [Birger, 1995]:
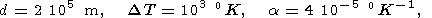 |
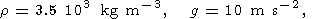 | (5) |
 |
Equations (3) were written in the Boussinesq
approximation, which is valid if several
dimensionless parameters are small; one of these parameters
is
aDT. This
parameter is estimated for the lithosphere as
aDT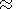 0.04. As the zero-order
approximation in the small parameter
aDT, the
upper
free-deformable surface of the layer, where stresses vanish,
behaves like a "free" boundary; i.e., the condition of zero
normal stress is replaced by a condition of zero vertical
velocity on this boundary. Let us suppose the lower boundary
of the layer to be also "free". Then, the boundary conditions
on the upper and lower surfaces of the layer are
0.04. As the zero-order
approximation in the small parameter
aDT, the
upper
free-deformable surface of the layer, where stresses vanish,
behaves like a "free" boundary; i.e., the condition of zero
normal stress is replaced by a condition of zero vertical
velocity on this boundary. Let us suppose the lower boundary
of the layer to be also "free". Then, the boundary conditions
on the upper and lower surfaces of the layer are
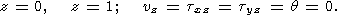 | (6) |
Note that the use (6) permits us to find an exact solution that is not significantly different from the numerical solutions obtained for more realistic boundary conditions [Birger, 1995, 1998].
The set of equations (1)-(6) has a solution in the form of a thermoconvective wave
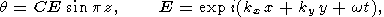 |
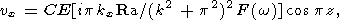 |
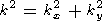 | (7) |
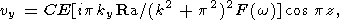 |
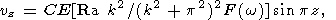 |
where C is an arbitrary complex factor (the amplitude of temperature), kx and ky are the components of wave vector describing the periodicity in the horizontal directions, k is the wave number, w is the complex frequency (its imaginary part describes the wave attenuation), and F(w) is the complex viscosity defined as
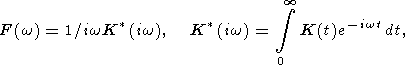 | (8) |
K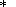 (iw)
being the Laplace transform of the creep kernel. The
complex viscosity is related to the wave number
k by
the dispersion relation
(iw)
being the Laplace transform of the creep kernel. The
complex viscosity is related to the wave number
k by
the dispersion relation
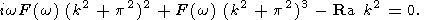 | (9) |
This allows to find such a value of the Rayleigh number Ra m (called the minimal critical Rayleigh number) that only a wave with k = km and frequency w = wm does not attenuate. For the Andrade rheological model, the complex viscosity is
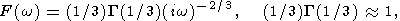 | (10) |
where G(x) is the gamma-function, and Ra m, km and wm take on the following values:
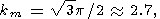 |
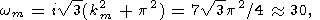 | (11) |
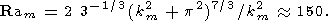 |
According to the estimated parameters the lithosphere
(5), the Rayleigh number Ra for the lithosphere is on the
same order of magnitude as Ra
m. Thus, the lithosphere is in
the state close to its instability threshold. If
Ra > Ram, the initial perturbations increase with time,
and at large
t, both the linearized equations of thermal convection
(3) and the linear rheological relationship (1) cannot be used.
If
Ra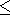 Ram, the solution of
the set of equations (1)-(6), for
a given but not too great initial perturbation of temperature,
completely describes the evolution of the perturbations in the
layer modeling the lithosphere.
Ram, the solution of
the set of equations (1)-(6), for
a given but not too great initial perturbation of temperature,
completely describes the evolution of the perturbations in the
layer modeling the lithosphere.
The solution (7)-(11) is obtained in the zero-order approximation in the small parameter aDT. In this approximation, the vertical displacement uz of the upper surface of the layer is equal to zero. In the the same approximation in aDT, we find
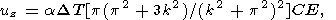 | (12) |
which does not depend on the rheology of the layer.
If the initial perturbation of temperature at t = 0 is given in the form
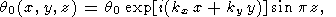 | (13) |
the factor C in (7) and (12) is defined as C = q0. However, the initial condition (13) does not completely determine the evolution of the perturbations. Since the wavenumber k, rather than the components kx and ky of the wave vector, enters the dispersion relation (9), in addition to the thermoconvective wave (7), there is a solution with the wave vector (-kx, -ky) describing the wave that runs in the opposite direction. The superposition of the waves, travelling in the opposite directions, forms a standing wave (thermoconvective oscillation). The solutions of governing equations (3)-(6) in the form of both running and standing waves satisfy the initial condition (13). This ambiguity is removed if the initial perturbation (13) is replaced by a more realistic initial perturbation that occupies a finite region and tends to zero for large x and y. Such centered initial perturbations are treated in the next sections of the paper.
In this case, the initial temperature perturbation will be given as
where q0(x, y) is not zero only in a limited area on the plane xy, and the solution is sought for in the form
Thus, the dependence of the solution on z is fixed, and hence, the problem of three-dimensional distribution of temperature perturbation in the lithosphere is reduced to a two-dimensional problem. In the case, when the initial temperature perturbation does not depend on y and has the form q0(x), the problem of two- dimensional temperature distribution is reduced to a one-dimensional problem.
The solution in the form of thermoconvective wave is valid for a sufficiently large time elapsing from the moment of the perturbation onset. Under this condition, the stresses harmonic in time induce strains also harmonic in time in the rheological model (1), and the complex analog of viscosity (10) depends only on the frequency, rather than on time.
When the initial temperature perturbation is given in the form (13), we seek a solution of convection equations in the form
Thus, the coordinate of the temperature and velocity remains in the same form as (7) and the problem reduces to the determination of the time dependence. We seek the solution for k = km and Ra = Ra m, whose the values are found in (11).
THe Laplace transformation of the basic equations (1) and (3) and the elimination of all of the physical variables, except the temperature, yields the Laplace transform of the desired function q(t)
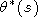 |
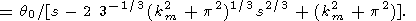 | (14) |
The viscosity analog is now the function
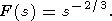 | (15) |
Rearranging the denominator of the expression in the right-hand side of (14),
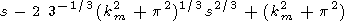 |
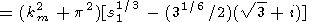 | (16) |
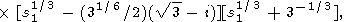 |
where s1 = s/(k2m + p2).
Since
 i)]3
=
i)]3
=  i31/2, (-3-1/3)3
= -1/3,
i31/2, (-3-1/3)3
= -1/3,
we may assume that the expression (16) is zero when
s1 = i31/2,
s1 = -i31/2 and
s1 = -1/3.
However, expressions (10) and (15) for
the complex viscosity imply that only the first value of the
root, for which the argument of the complex number s satisfies
the condition
0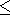 arg s < 2p,
must be used.
Then,
arg s < 2p,
must be used.
Then,
and hence, (16) is zero for s1 = i31/2 but not for s1 = -i31/2 and s1 = -1/3. The Laplace transform (14) can be rewritten as
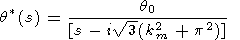 | |
| (17) | |
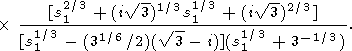 |
This expression has two singularities: at the branch point s = 0 and at the pole s = i31/2(k2m + p2). In the vicinity of point s=0,
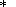 (s)
(s)
| (18) |
 ],
],
and in the vicinity of point s = i31/2(k2m + p2),
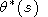 |
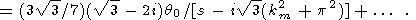 | (19) |
Using the theorem on the asymptotic behavior of Laplace originals [e.g., Von Doetsch, 1967], we find the following asymptotic solution for large t
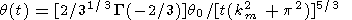 |
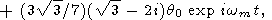 | (20) |
where
wm = 31/2(k2m
+ p2),
which corresponds to (11). The
first aperiodic term in the right-hand side of (20) is much
smaller than the second, periodic term, even for
t equal to the oscillation period
2p/wm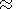 1/5.
Thus, for
t
1/5.
Thus, for
t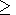 2p/wm, the solution takes the form
2p/wm, the solution takes the form
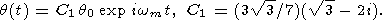 | (21) |
Since
|C1|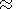 2, the amplitude of steady-state
thermoconvective wave
is two times greater than the initial amplitude of
temperature perturbation
q0. The argument of complex number
C1 defines a phase difference. In the next sections of the paper,
the factor
C1, which
appears in the transient process, is omitted for brevity.
2, the amplitude of steady-state
thermoconvective wave
is two times greater than the initial amplitude of
temperature perturbation
q0. The argument of complex number
C1 defines a phase difference. In the next sections of the paper,
the factor
C1, which
appears in the transient process, is omitted for brevity.
Taking ky = 0 and kx = k, we first consider only one-dimensional perturbations independent of the coordinate y. Expanding the complex frequency into the Taylor series in the neighborhood of k - km,
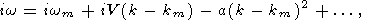 | (22) |
where the coefficient V means the group velocity of a packet of thermoconvective waves. Substituting (22) into the dispersion relation (9), we find the values of the coefficients in (22) for the Andrade model
The group velocity V of thermoconvective waves in a medium with the Andrade rheology is slightly lower than the phase velocity wm/km = 7p/2.
The initial temperature perturbation q0(x) is represented in the form of the Fourier integral
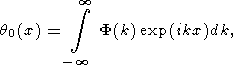 | (23) |
where F(k) is the Fourier transform of the initial temperature
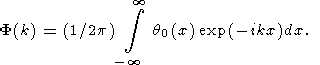 | (24) |
The solution satisfying the initial condition is represented as
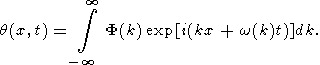 | (25) |
Substituting the expansion of frequency (22) into (25) and denoting k - km = u, we obtain
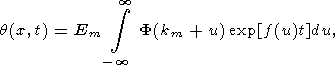 | (26) |
where the integration is actually taken over a small vicinity of the point u = 0 (k = km) and the following notation is introduced
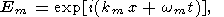 |
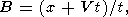 | (27) |
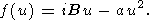 |
The integral in (26) can then be evaluated by the saddle point method [e.g., Copson, 1965]. The stationary point u0 is found from the condition
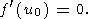 | (28) |
Equations (27) and (28) give
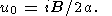 | (29) |
In the vicinity of point u0, function f(u) is represented by the series
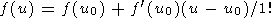 |
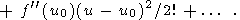 | (30) |
Since
f (u0) = 0
and
f
(u0) = 0
and
f
 (u0)
= -2a,
(30) takes the form
(u0)
= -2a,
(30) takes the form
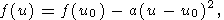 | (31) |
where only two first terms of expansion are retained.
Substituting (31) into (26),
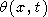 | (32) |
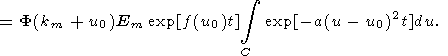 |
The point u0 is the saddle point for the complex function f(u). According to the saddle point method, the path of integration on the complex plane is chosen in such a way that it passes through point u and, in the small vicinity of this point, the path is a segment of the staight line on which the function f(u)-f(u0) is real and negative. In the vicinity of u0,
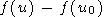 |
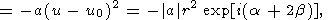 | (33) |
where
It is clear from (33) that the straight line for which b = -a/2 must be chosen as the path of integration. On this straight line, the function f(u)-f(u0) takes on real negative values and the integral in (32) reduces to the simple expression
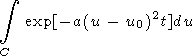 |
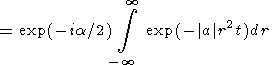 |
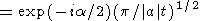 | (34) |
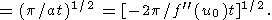 |
In transformation (34), the integral is reduced to the real
error integral, and the transition to the infinite
limits of
integration can be made under the condition
|a|t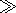 1. Since
|a|
1. Since
|a|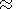 10,
the result given by (34) is holds true for
t
10,
the result given by (34) is holds true for
t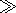 1/10.
1/10.
Thus, the solution in the case of an arbitrary initial perturbation has the form
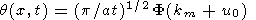 |
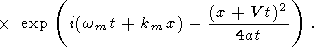 | (35) |
This is a wave packet moving to the left. To obtain the total solution, a term corresponding to the wavenumber k = -km must be added to the right-hand side of (35). This term, which is readily obtained by changing the sign of km and V in the right-hand side of (35), describes a wave packet moving to the right.
The quantity
x = x + Vt can be interpreted as
a coordinate in
the reference frame that moves together with the wave packet at
the group velocity
V. The right-hand side of (35) goes to zero at
x2/4|a|t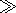 1. The width of the wave packet can be considered to be
of the order of
2(2|a|t)1/2 ; i.e., the wave packet exists only
for
|x|
1. The width of the wave packet can be considered to be
of the order of
2(2|a|t)1/2 ; i.e., the wave packet exists only
for
|x|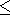 (2|a|t)1/2.
Under this condition, it follows from (29)
that
(2|a|t)1/2.
Under this condition, it follows from (29)
that
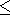 (2|a|t)1/2.
(2|a|t)1/2.
Since
|a|t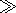 1, we find that
|u0|
1, we find that
|u0|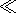 km.
Consequently, in
the expression
F(km + u0)
in (35) can be replaced with
F(km).
km.
Consequently, in
the expression
F(km + u0)
in (35) can be replaced with
F(km).
In the case when the initial perturbation of temperature takes place in a fixed point x = 0, function q0(x) and its Fourior transform are written as
 | (36) |
where d(x) is the delta-function satisfying the relationship
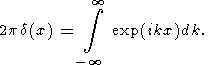 |
Note that (36) retains its form in the dimensional variables since the delta-function has the dimension of reciprocal length and the quantity Q0 has the dimension of temperature multiplied by length.
As follows from (35), the asymptotic
(|a|t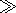 1) solution
under the initial condition (36) takes the form
1) solution
under the initial condition (36) takes the form
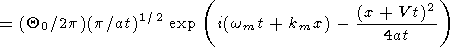 |
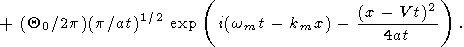 |
This solution represents two wave packets running in the opposite directions from the point x = 0, where the initial perturbation takes place. The distributions of temperature at fixed moments of time are shown in Figure 1.
Let the initial perturbation be represented by the sum of two delta functions
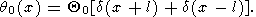 | (37) |
The Fourier transform of (37) is
but it cannot be used in the problem with the
initial condition (37) because its solution is
a simple superposition of two solutions obtained for the initial
perturbations specified at points
x=l and
x=-l. Four
wave packets move away from these points: two of them move From
x = l toward the left and the other two move from
x = -l toward the right. Their velocities are
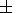 V, respectively. At the
moment
t0 = l/V, the centers of the packets, moving in the
opposite directions, meet each other at point
x=0. The perturbation of temperature at
-l
V, respectively. At the
moment
t0 = l/V, the centers of the packets, moving in the
opposite directions, meet each other at point
x=0. The perturbation of temperature at
-l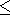 x
x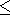 l is the superposition of two wave packets
l is the superposition of two wave packets
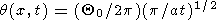 |
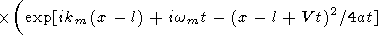 | (38) |
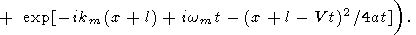 |
Denoting t1 = t - t0 ( t1 is positive after the meeting and negative before it), substituting t = t0 + t1 into the right-hand side of (38) and observing that
after algebraic transformations, we obtain
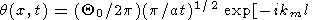 |
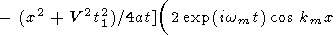 |
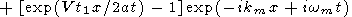 | (39) |
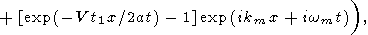 |
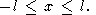 |
Thus, (39) represents the perturbation of temperature as the superposition of a standing wave and two running waves moving in the opposite directions. The amplitudes of the running waves is zero for small x and t1, and in the vicinity of x = 0, the solution (39) reduces to
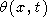 |
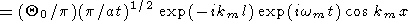 | (40) |
Equation (40) holds for
|x|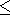 Dx
and
|t1|
Dx
and
|t1|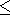 Dt,
where
2Dx is the width of the standing wave zone,
2Dt is the lifetime of the standing wave.
These quantities are estimated as
Dt,
where
2Dx is the width of the standing wave zone,
2Dt is the lifetime of the standing wave.
These quantities are estimated as
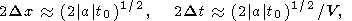 | (41) |
where
|a|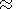 10. The typical dimension of a craton
is on
the order of 2000 km, which corresponds to
l
10. The typical dimension of a craton
is on
the order of 2000 km, which corresponds to
l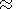 10. Then,
t0 = l/V
10. Then,
t0 = l/V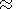 1,
the width of standing wave zone is
2Dx
1,
the width of standing wave zone is
2Dx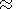 5, and its lifetime is
2Dt
5, and its lifetime is
2Dt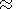 1/2. Since the wavelength is
2p/km
1/2. Since the wavelength is
2p/km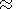 2 and the period of
convective oscillation is
2p/wm
2 and the period of
convective oscillation is
2p/wm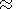 1/5,
the zone of standing wave
envelops two wavelengths, and two periods of oscillation
occur for the lifetime of the standing wave.
1/5,
the zone of standing wave
envelops two wavelengths, and two periods of oscillation
occur for the lifetime of the standing wave.
Consider another example of the initial perturbation
 |
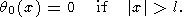 | (42) |
The Fourier transform for function (42) is
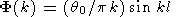 |
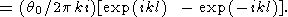 | (43) |
With transform (43), the solution is
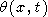 |
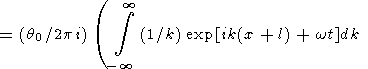 | (44) |
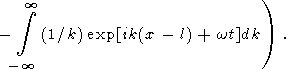 |
Since the dominant contribution to the integral in (44) comes from small vicinities of points k = km and k = -km, (44) can be rewritten in the form
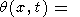 |
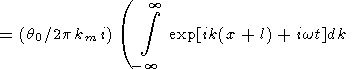 |
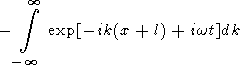 | (45) |
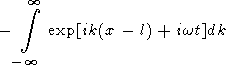 |
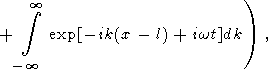 |
where w is a function of k and w(km) = wm. Each of the four integrals in (45) describes a wave packet associated with the initial perturbation in the form of d -function. The first packet moves from point x = -l toward the left, the second one moves from x = -l toward the right, the third one moves from x = l toward the left, and the fourth one moves from x = l toward the right. The first and fourth packets move outward from the initial region of temperature perturbation, and the second and third packets move inward this initial region. When they meet, the standing wave is formed in the vicinity of x = 0, like in the problem with the initial condition given by the sum of two delta functions.
Considering two-dimensional perturbations, we introduce, for brevity, the notation kx = p and ky = q. Then,
 | (46) |
The complex frequency w is expanded in the power series
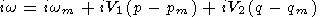 |
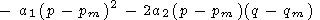 | (47) |
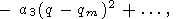 |
where
 |
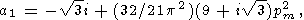 |
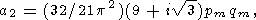 | (48) |
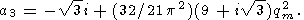 |
The solution, satisfying the initial conditions, is written as
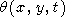 |
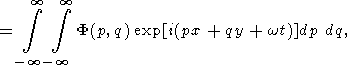 | (49) |
where F(p, q) is the Fourier transform of the initial temperature distribution q0(x, y)
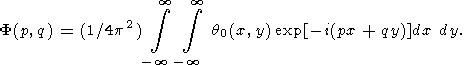 |
Substituting (47) for w into (49), we get
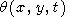 |
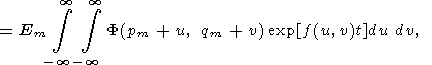 | (50) |
where
The stationary point (u0, v0) of the function f(u, v) is defined by the condition
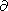 f/
f/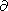 u =
u = 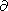 f/
f/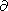 v = 0,
v = 0, which allows us to find
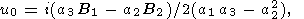 |
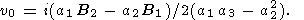 | (51) |
Since
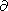 2 f/
2 f/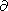 u2 = -2a1,
u2 = -2a1, 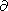 2 f/
2 f/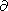 u
u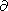 v = -2a2,
v = -2a2,
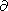 2 f/
2 f/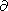 v2 = -2a3,
v2 = -2a3, the function in the neighborhood of point (u0, v0) is represented as
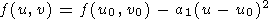 |
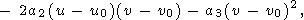 | (52) |
where
Substituting expansion (52) into (50),
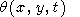 |
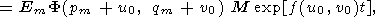 | (53) |
where
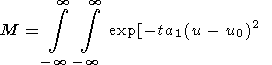 |
Using the substitution
M is represented in the form
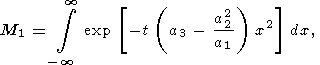 |
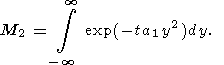 |
Evaluating the integrals M1 and M2 by the saddle point method, we reduce (53) to
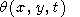 |
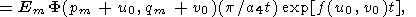 | (54) |
where
The wave vector components pm and qm, satisfying condition (46), can be represented as
 | (55) |
where j varies from 0 to 2p. Since all the directions of the wave vector (pm, qm) are equivalent, the integration over j is implied in the right-hand sides of (53) and (54).
If the initial perturbation takes place at point (0, 0), then
and we must substitute in (54) the Fourier transform of this function
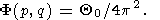 | (56) |
It is convenient to introduce the polar coordinates r and y
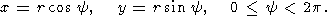 | (57) |
As follows from (55) and (57), the factor Em in (54) becomes
Thus, the temperature perturbation q induced by the initial point-concentrated perturbation is given by the equation
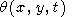 |
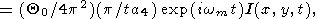 |
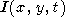 | (58) |
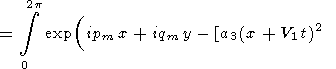 |
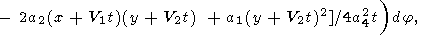 |
where the dependence of integrand on j is defined by equations (48) and (55). Since it is clear that q depends on r rather than on y, for the case of the initial point-concentrated perturbation, we can take y = 0 (and hence x = r, y = 0 ) in the integrand. Then,
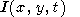 |
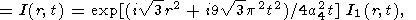 |
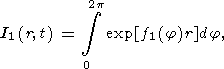 | (59) |
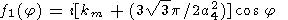 |
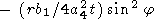 |
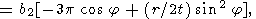 |
where
The integral I1(r, t) at large r is calculated using the saddle point method
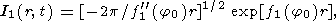 | (60) |
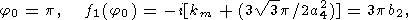 | (61) |

 1
(j0) = i[km
+ (33p/2a24)]-rb1
/2a24 t = b2 [(r/t)-3p].
1
(j0) = i[km
+ (33p/2a24)]-rb1
/2a24 t = b2 [(r/t)-3p].
After simple algebraic transformations, we find an asymptotic solution (valid only for sufficiently large t and r ) of the problem with the initial condition specified at the given point:
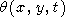 |
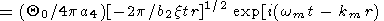 | (62) |
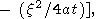 |
where
Note that parameter a has already appeared in the one-dimensional problem. Solution (62) describes a cylindrical wave because the dependence on coordinates reduces to the dependence only on r = (x2 + y2)1/2.
The function f1(j) introduced in (59)-(61), in addition to the saddle point j0 = p, has the second saddle point j0 = 0. The use of the latter would lead to an additional term in the right-hand side of (60). This term describes a wave running to the point r = 0 from outside and includes the factor
which becomes zero for sufficiently large positive r and t.
In the center of the wave packet, i.e., at
x = 0 (r = 3pt),
equation (62) violates. When
x = 0,
the second derivative
f
 1(j0) is zero (the third derivative is also
zero).
In this case, the saddle point method leads to
1(j0) is zero (the third derivative is also
zero).
In this case, the saddle point method leads to
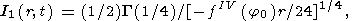 | (63) |
instead of (60). Note that
G(1/4)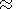 4.
The derivation of the
asymptotic relation (63) that holds for large
r, is analogous to
that of (30)-(34), with the exception that the
Taylor series is trancated at the term including the fourth
derivative, and furthermore, the integral
4.
The derivation of the
asymptotic relation (63) that holds for large
r, is analogous to
that of (30)-(34), with the exception that the
Taylor series is trancated at the term including the fourth
derivative, and furthermore, the integral
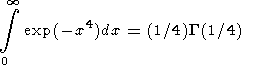 |
is used instead of the error integral.
Substituting the value of the fourth derivative
into (63), we find the solution valid in the small vicinity of
the wave packet center, i.e., at
r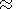 3pt,
3pt,
| (64) |
A simplified approach of this section to the problems under consideration is not to expand w in the power series but to set w = wm for values of k = (p2 + q2)1/2 close to km in equation (49). Then,
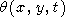 |
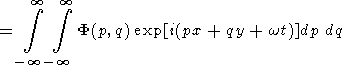 |
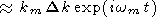 | (65) |
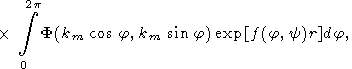 |
where
Here the polar coordinates are used and the integral is taken over
a ring on the plane
p, q. The radius of the ring is equal to
km, but
its thickness
Dk is indeterminate in the framework of
the
simplified approach
used now. In the interval
0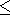 j< 2p,
function
f(j, y)
has the following stationary points
j< 2p,
function
f(j, y)
has the following stationary points
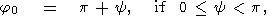 |
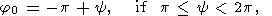 | (66) |
For the initial perturbation in the form of delta function (an elementary radiator of thermoconvective waves), substituting F = Q0/4p2 into (65), using the saddle point method, and omitting the solution corresponding to the saddle point j0 = y (a wave arriving at point r = 0 from outside), we find the solution for large r
| (67) |
In contrast to solution (62), which takes into account the wavenumber dependence of w (i.e., dispersion), equation (67) describes a wave with nonmodulated amplitude. It is noteworthy that the simplified approach gives the factor r-1/2 in (67), which determines attenuation of any cylindrical wave [e.g., Whitham, 1974]. Comparison of solution (67) with solutions (62) and (64) shows that, in order to take the dispersion into account, it is enough to substitute into (67) the following expressions for Dk
| (68) |
We then use the same simplified approach for the case when the initial perturbation has the form
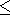 x
x 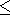 l, -l
l, -l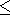 y
y 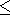 l,
l,
that is, the uniform temperature perturbation q0 at the initial moment is given within a square with a side 2l. For such initial condition,
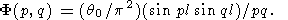 | (69) |
It is convenient to rewrite (69) in the form
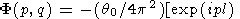 |
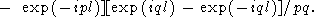 | (70) |
Substituting (70) into (65),
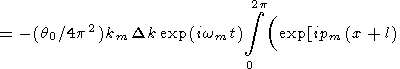 |
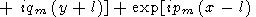 | (71) |
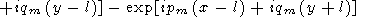 |
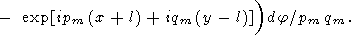 |
Consider separately the integral corresponding to the first term. The vector ( x + l, y + l ) connects the apex (-l, -l) of the square with the point (x, y). Introducing a polar coordinate system whose origin is located at this apex,
 | (72) |
Then,
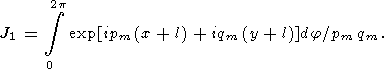 |
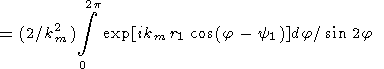 | (73) |
Using the saddle point method and omitting the term that describes the wave running to the apex from outside, we obtain the expression for J1 at sufficiently large r1
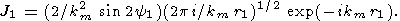 | (74) |
Equation (74) is valid when y1 is outside of a small vicinity of points 0, p/2, p, and 3p/2. Substituting these values of y1 into (73), we readily verify that the integral J1 goes to zero for these values of y1.
The total solution is obtained as the sum of four integrals
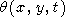 |
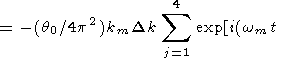 | (75) |
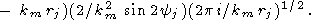 |
Here, the angles y3 and y4 corresponding to the apexes (l, -l) and (-l, l) are measured clockwise, whereas y1 and y2 are measured counter-clockwise. Substituting
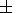 l)2
+ (y
l)2
+ (y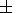 l)2]1/2,
yj = arctan [(y
l)2]1/2,
yj = arctan [(y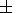 l)/(x
l)/(x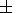 l)],
l)],
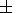 l)2 + (y
l)2 + (y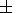 l)2]/2(x
l)2]/2(x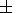 l)(y
l)(y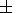 l),
l), into (67), we write the solution in the form
where
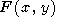 |
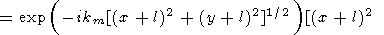 |
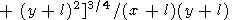 |
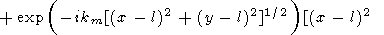 |
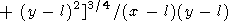 | (76) |
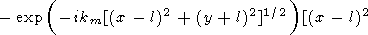 |
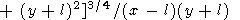 |
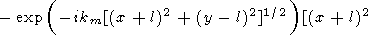 |
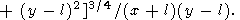 |
Equation (76) is valid for all
x and
y except the points located
on the lines
x = 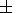 l,
y =
l,
y = 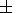 l and in the neighborhood of
these lines
having the width of the order of the wavelength
2p/km.
l and in the neighborhood of
these lines
having the width of the order of the wavelength
2p/km.
Introducing the polar coordinates x = r cosy, y = r siny and using the simple relationship
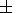 l)2 + (y
l)2 + (y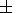 l)2]1/2 = r + l(
l)2]1/2 = r + l(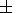 cosy + siny),
r
cosy + siny),
r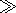 l,
l,
we obtain that, for
r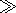 l (the great distance from the
initial square), solution (76) reduces to
l (the great distance from the
initial square), solution (76) reduces to
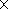
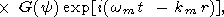 | (77) |
where
Equation (77) describes the wave running outside from the
initial square. Note that
G and hence the right-hand side of
(77) does not depend on
y only under the condition
kml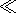 1 (the length
of the side of the initial square is small in comparison with
the thermoconvective wavelength). Under this condition, the
initial pertur-bation given in the square acts like an initial
pointwise perturbation.
1 (the length
of the side of the initial square is small in comparison with
the thermoconvective wavelength). Under this condition, the
initial pertur-bation given in the square acts like an initial
pointwise perturbation.
 Function
G(y) is plotted for various values of
l in
Figure 2.
The directivity pattern of the thermoconvective radiation
is defined by the amplitude factor
|G(y)|.
As follows from the plots in Figure 2,
the directions of the most intense radiation are
y = 0,
y = p/2,
y = p,
y = 3p/2. When
l
Function
G(y) is plotted for various values of
l in
Figure 2.
The directivity pattern of the thermoconvective radiation
is defined by the amplitude factor
|G(y)|.
As follows from the plots in Figure 2,
the directions of the most intense radiation are
y = 0,
y = p/2,
y = p,
y = 3p/2. When
l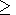 2, the real function
G(y) periodically changes its sign, and
hence,
arg G(y) takes on the
values 0 or
p. Thus, the phase of the wave described by (77),
as well as the
amplitude, is direction-dependent.
2, the real function
G(y) periodically changes its sign, and
hence,
arg G(y) takes on the
values 0 or
p. Thus, the phase of the wave described by (77),
as well as the
amplitude, is direction-dependent.
In the theory of radiation, a radiator whose dimensions are
much smaller than the radiated wavelength is called simple.
The simple radiator has an omnidirectional radiation. A composite radiator
is one whose dimensions are not small compared to the
wavelength and which emits a directional radiation. Thus, the
square where the temperature is initially perturbed is a
simple radiator of thermoconvective waves
if
kml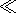 1, but this
square is a composite radiator if
kml > 1.
1, but this
square is a composite radiator if
kml > 1.
In order to account for the dispersion that leads to the amplitude and phase modulation, it is enough to substitute the expressions (68) for Dk into (77).
For
r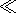 l (in the neighborhood of the center
of the
initial square), the following relationship takes place
l (in the neighborhood of the center
of the
initial square), the following relationship takes place
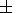 l)2 + (y
l)2 + (y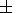 l)2]1/2 = 21/2l
+ (21/2/2)r (
l)2]1/2 = 21/2l
+ (21/2/2)r (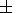 cosy
cosy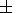 siny),
siny),
where
21/2l is the distance between the apex and the center of
the square. By using this approximate equation, we reduce
(76) for
r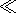 l to the form
l to the form
| (78) |
where
As is seen from (78), a standing wave with square cells is
formed in the central part
(r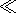 l) of the initial square. The
sides of the cells are parallel to the sides of the initial square
and the length of the cell side is
21/2p/km.
The same standing wave is formed
in the neighborhood of the point (0,0) in the case when the
initial temperature perturbation is given at four points:
(l, l),
(l, -l),
(-l, l), and
(-l, -l) i.e. when the initial perturbation
square is replaced by the pointwise perturbation at its apexes.
l) of the initial square. The
sides of the cells are parallel to the sides of the initial square
and the length of the cell side is
21/2p/km.
The same standing wave is formed
in the neighborhood of the point (0,0) in the case when the
initial temperature perturbation is given at four points:
(l, l),
(l, -l),
(-l, l), and
(-l, -l) i.e. when the initial perturbation
square is replaced by the pointwise perturbation at its apexes.
Note that in order to obtain the solution (77), valid for
r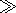 l,
we could use the expression (69) for
F. We represents
F in the
form (70) to find the solution for
r
l,
we could use the expression (69) for
F. We represents
F in the
form (70) to find the solution for
r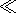 l i.e. in the neighborhood
of the center of the initial square. The result (78), obtained
by the saddle point method, is holds true under the condition
kml
l i.e. in the neighborhood
of the center of the initial square. The result (78), obtained
by the saddle point method, is holds true under the condition
kml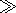 1.
(length of the side of the initial square is much greater
then thermoconvective wave length). This condition is satisfied when
the initial temperature perturbation covers a craton as a
whole, and therefore,
l
1.
(length of the side of the initial square is much greater
then thermoconvective wave length). This condition is satisfied when
the initial temperature perturbation covers a craton as a
whole, and therefore,
l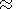 10. for
km = 2.7.
10. for
km = 2.7.
The distribution of temperature in the lithosphere is represented in the form
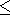 z
z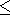 1,
1,
where
q(x, y, t) can be interpreted
as a temperature
perturbation in the middle of the lithosphere
(z = 1/2).
The temperature
perturbation
q(x, y, t) is found under
a few simple initial
conditions: the initial perturbations
q0(x, y) are given on
the straight line
(x = 0), in the strip
(-l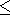 x
x l), at the point ( x = 0,
y = 0 ), at
four points, or within a square.
l), at the point ( x = 0,
y = 0 ), at
four points, or within a square.
For a plane thermoconvective wave with the wave vector (kx, ky), the displacement of the upper surface of the layer (lithosphere) is related to the temperature perturbation by (12). This relation is easily generalized to the case of a packet of thermoconvective waves with the wave numbers close to km
When more real boundary conditions on the upper and lower surfaces of the lithosphere are considered [Birger, 1988], the dependence of temperature perturbation on the vertical coordinate z is not determined by the function sin pz and the wave number km is not equal to 2.7. However, the displacement uz(x,y,t) remains equal to the temperature perturbation q(x,y,t) multiplied by a constant whose value depends on the boundary conditions. This is also valid for the case when the depth dependence of physical parameters (in particular, the Andrade rheological parameter) of the lithosphere is taken into account. Thus, functions q(x, y, t), found above under various initial conditions, describe the vertical displacements of upper surface of the lithosphere, with accuracy to a constant factor. These displacements determine sedimentary processes.
The initial temperature point-concentrated perturbation can be treated as a source of thermoconvective waves in the lithosphere. When the initial perturbation occupies a finite area, thermoconvective waves propagate outward from this area and thermoconvective oscillations (standing waves) are settled inside the area. The thermoconvective oscillations create a system of convective cells in the lithosphere. Over the convective cells, the surface of the lithosphere subsides (or rises) forming sedimentary basins. Since the Rayleigh number for the lithosphere is not greater than Ra m, the shape of cells and hence the shape of basins is determined by initial perturbations. The initial perturbation in the square considered above leads to the appearance of square cells. However, other initial conditions may lead to rectangular, hexagonal, and other shapes of cells and basins.
Thermoconvective oscillations may be considered as a mechanism inducing the formation and evolution of sedimentary basins on continental cartons [Birger, 1998]. In this paper, we have studied the excitation of thermoconvective waves and oscillations by initial perturbations of temperature. Note that these waves are also generated from initial vertical displacements of the Earth's surface (relief perturbations).
Packets of thermoconvective waves propagate in the
lithosphere with the velocity
3pk/d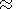 0.15 cm/year and create
sediment-filled depressions on the upper
surface of the lithosphere. The age of sediments increases
proportionally to the
distance from the front of the wave to its source.
Thermoconvective
waves may be related to the development of peripheral
depression on a craton. In this process known in geology
[Beloussov, 1978; Khain, 1973],
the initial depression occurring in a
geologically active area ("geosyncline") adjacent the craton
slowly develops within the craton.
0.15 cm/year and create
sediment-filled depressions on the upper
surface of the lithosphere. The age of sediments increases
proportionally to the
distance from the front of the wave to its source.
Thermoconvective
waves may be related to the development of peripheral
depression on a craton. In this process known in geology
[Beloussov, 1978; Khain, 1973],
the initial depression occurring in a
geologically active area ("geosyncline") adjacent the craton
slowly develops within the craton.
Beloussov, V. V., Endogenous Regimes of Continents, Nedra, Moscow, 1978 (in Russian).
Birger, B. I., Linear and weakly nonlinear problems of the theory of thermal convection in the earth's mantle, Phys. Earth Planet. Inter., 50, 92-98, 1988.
Birger, B. I., On the thermoconvective mechanism for oscillatory vertical crustal movements, Phys. Earth Planet. Inter., 92, 279-291, 1995.
Birger, B. I., Rheology of the Earth and thermoconvective mechanism for sedimentary basins formation, Geophys. J. Inter., 134, 1-12, 1998.
Copson, E. T., Asymptotic Expansions, University Press, 170 pp., Cambridge, 1965.
Fleitout, L., and Yuen, D. A., Steady state, secondary convection beneath lithosphere plates with temperature- and pressure-dependent viscosity, J. Geophys. Res., 89, 9227-9244, 1984.
Khain, V. E., General Geotectonics, 512 pp., Nedra, Moscow, 1973 (in Russian).
Von Doetch, G., Anleitung zum praktischen Gebrauch der Laplace-Transformation und der Z-Transformation, Springer, 365 pp., Munich, 1967.
Whitham, G. B., Linear and Nonlinear waves, John Wiley and sons, New York, 1974.
 |