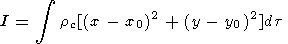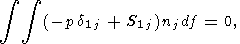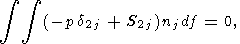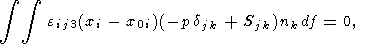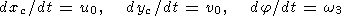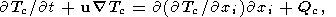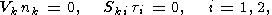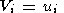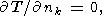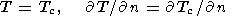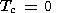Russian Journal of Earth Sciences
Vol 1, No. 2, December 1998
Translated February 1999
3-D Spherical models for mantle convection, continental
drift, and the formation and disintegration of
supercontinents
V. P. Trubitsyn and V. V. Rykov
Shcmidt United Institute of Physics of the Earth, Russian Academy
of
Sciences, B. Gruzinskaya ul. 10, Moscow, 123810 Russia
Contents
Abstract
One of the most important problems of geoscience is to
explain the drift mechanism of continents uniting
periodically to form supercontinents similar to Pangea. This
work presents for the first time a numerical model of mantle
convection in a 3-D spherical mantle with drifting
continents. The mantle is modeled by a viscous fluid
developing thermal convection upon heating. When the
drifting continents are placed into the mantle, they start
drifting under the effect of the forces of viscous coupling
with mantle convection flows. Subject to numerical solution
is the set of mass, heat, and momentum transfer equations
for convection in the viscous mantle and the associated set
of Euler equations for the movement of the solid continents.
The mantle and continents interact with one another
mechanically in the course of heat exchange. In order to
better understand the mantle-continent interaction
processes, we have analyzed two models, one with a single
continent and a weak thermal convection with a Rayleigh
number of 10
4 and the other with five continents and an
intense thermal convection with a Rayleigh number of 10
6.
In the case of weak convection, there form in the mantle but
a few ascending and descending flows. The drifting continent
is pulled into one of the descending flows. As the size and
shape of the continent differ from those of the descending
flow zones, its position proves unstable, so that it drifts
constantly. In the absence of other continents and any
external forces, the continent moves along the descending
flow system. At higher Rayleigh numbers, convection becomes
nonstationary, in which case the number, shape, and position
of mantle convection flows vary constantly. What is more, if
there are several continents, the motion of each one of them
becomes bound and more complex. The continents can collide
directly, as well as interact with one another through the
intermediary of the mantle and thus change the structure of
its convection. The numerical experiments performed
demonstrate the possibility of both a partial uniting of
several continents and the formation of a single
supercontinent like Pangea upon the uniting of all the
continents.
1. Introduction
In the 70's, there occurred radical changes in the notions
of the processes taking place in the Earth's bowels and
their manifestations on the Earth's surface. Being able to
study the processes occurring on the bottom of the oceans,
American and European scientists discovered that the oceanic
lithosphere moves away from the mid-oceanic ridges. In the
ridges, the oceanic lithosphere is being born upon the
solidification of the erupting magma, and in the subduction
zones, the cooled lithosphere that has grown heavier is
being pulled back into the mantle. The entire Earth's
lithosphere gets broken down in the process into individual
plates some of which bear the continents. These notions were
formulated in the form of the concept of the tectonics of
oceanic lithospheric plates. The plate tectonics concept is
being understood not only in this narrow sense, but also in
a wider sense wherein it is being associated with the
formulation of the notions of the principal global processes
occurring in the Earth's mantle and manifesting themselves
in the motion of the lithospheric plates.
In the same 60-s - 70-s, the first reliable models for the
distribution of density, pressure, and temperature in the
Earth were constructed on the basis of measurement data on
the seismic wave velocities and experimental and theoretical
data on the properties of matter at high pressures.
Density in the mantle grows higher with depth largely not
because of changes in its chemical composition, but as a
result of changes in its compressibility and the phase
transformations consequent upon the rise of pressure.
Temperature in the mantle is extremely high, so that the
material therein, if exposed to it for a long time, becomes
capable of flowing like a highly viscous fluid. The
conclusion was drawn on this basis that in the mantle there
can occur an intense thermal convection.
The material circulating in the mantle cools down as it
rises to the surface and solidifies at a temperature of the
order of
T = 1300o C, forming
the semirigid oceanic
lithosphere. As it moves over the horizontal section of the
convection cell, the lithosphere cools still more and grows
thicker. In the descending section of the convection cell,
the immersed lithosphere stays semirigid for a long time,
until it gets heated to a temperature of
T
= 1300o C, forming
the semirigid oceanic
lithosphere. As it moves over the horizontal section of the
convection cell, the lithosphere cools still more and grows
thicker. In the descending section of the convection cell,
the immersed lithosphere stays semirigid for a long time,
until it gets heated to a temperature of
T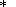 . Thus, the
oceanic lithosphere does not float on the surface of the
underlying portion of the mantle, but takes part in the
convective circulation of the mantle material in the entire
mantle cell and comprises that portion of the mantle which
at a given instant is at a temperature below
T
. Thus, the
oceanic lithosphere does not float on the surface of the
underlying portion of the mantle, but takes part in the
convective circulation of the mantle material in the entire
mantle cell and comprises that portion of the mantle which
at a given instant is at a temperature below
T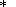 . The
horizontal size of convection cells being no more than 20
thousand kilometers and the maximum mantle convection flow
velocity, of the order of 10 centimeters per year, the age
of the oceanic lithosphere cannot exceed 200 million years.
. The
horizontal size of convection cells being no more than 20
thousand kilometers and the maximum mantle convection flow
velocity, of the order of 10 centimeters per year, the age
of the oceanic lithosphere cannot exceed 200 million years.
According to plate tectonics, there are no purely
continental plates. The continents are believed to be
permanently frozen into oceanic plates, and so can only
passively move together with them. Thanks to their buoyancy,
the continents cannot sink in the mantle. In contrast to the
oceanic lithosphere whose thickness is no more than 80 km,
the lithospheric roots of the continents may reach down to a
depth of a few hundreds of kilometers. But they do not
impede the drift of the continental plates, for the entire
mantle, all the way down to the core, behaves like a viscous
fluid. It should be noted that the subcrustal lithosphere of
the continents, like the oceanic lithosphere, is a region of
the mantle that only differs from the rest of the mantle by
its rheological properties and can, in principle, also be
mixed by convective mantle convection flows.
Numerous numerical experiments were conducted to date to
investigate thermal convection in the Earth's mantle. 2- and
3-D models in orthogonal and spherical coordinate systems
were used to reveal the role of variable, temperature-,
pressure-, and stress-dependent viscosity and the effect of
phase transformations on the structure of mantle convection
flows (see, for example,
[Christensen, 1983, 1984;
Christensen and Yuen, 1984;
Glatzmaier, 1988;
Lenardic and Kaula, 1994;
Machetel and Weber, 1991;
Parmentier et al., 1994;
Solheim and Peltier, 1994;
Tackley et al., 1994]).
It has been demonstrated in these models that the highly
viscous oceanic lithosphere can, on the whole, form in a
self-consistent manner, considering the fact that the
viscosity of the mantle material increases sharply with
temperature, especially in the vicinity of the
solidification point [Jacoby and Shmeling, 1982]. Despite
the great success of numerical modeling in the study of
mantle convection and oceanic lithosphere as a whole, plate
tectonics remains incomplete. The principal problem of plate
tectonics is still to be solved. No models have as yet been
constructed that can describe in a self-consistent fashion
the breakdown of the oceanic lithosphere into individual
plates.
Plate tectonics explains the origin and evolution of the
oceanic lithosphere alone. As noted earlier, the continental
lithosphere possesses substantially different properties in
comparison with its oceanic counterpart. It is much thicker,
and its age is also much greater. The plate tectonics'
proposition that there exist no purely continental plates
only refers to a short interval of time, less than the
average age of the oceanic plates. In the course of 200
million years, all the oceanic plates get immersed into the
mantle. But the continents, though capable of deformation,
fragmentation, and uniting, exist for a few billions of
years. They cannot therefore be regarded as passive
inclusions in oceanic plates. If the continents drifted
passively, being frozen into the oceanic plates, it would
also be impossible to explain the causes of disintegration
of supercontinents [Trubitsyn and Rykov, 1995].
Based on the measurements taken on the ocean floor, it
proved possible to study the properties of the oceanic
lithosphere. But the continental lithosphere is hidden
beneath the thick continental crust. For this reason, the
properties of the continental lithosphere are now being
investigated by numerically modeling mantle convection
interacting with the drifting continents.
Trubitsyn and Fradkov [1985] have been the first to
demonstrate that thermal convection in the upper mantle
under the continents is suppressed and the heat flow through
the continents is reduced accordingly (by a factor of
three). At the same time, the oceanic lithosphere cannot
effectively impede the removal of heat from the mantle,
because the oceanic lithospheric plates participate in the
convective circulation of the mantle material. It has been
shown
[Bobrov and Trubitsyn, 1996;
Lowman and Jarvis, 1993, 1995,
1996;
Nakakuki et al., 1997;
Trubitsyn and Bobrov, 1994, 1996,
1997;
Trubitsyn et al., 1991, 1993a,
1993b, 1994]
that a stationary continent first suppresses mantle
convection beneath itself and extends the convection cell,
and then, a few hundreds of years later when the
subcontinental mantle gets heated, a hot ascending mantle
convection flow develops under the continent.
Insofar as the continents are not fixed in space but drift
over the mantle, their effect on the structure of mantle
convection proves even stronger. In the first works, account
was only taken of the mechanical interaction between the
mantle and mobile plates by formulating an effective
boundary condition. At the plate locations, the horizontal
drift velocity was specified instead of the free-boundary
condition
[Doin et al., 1997;
Lux et al., 1979;
Trubitsyn and Fradkov, 1986].
In his work of 1988, Gurnis presented the results of
calculation of a 2-D numerical mantle convection model
allowing for both mechanical and thermal interaction with
drifting continents. To prevent the spreading of the viscous
continents, use was made in that case of an implicit
technique fixing the extreme points of the continents.
[Rykov and Trubitsyn 1996a, 1996b;
Trubitsyn and Rykov 1995]
constructed the
first self-consistent 3-D numerical mantle convection model
with two drifting 3-D solid continents, based on the direct
solution of a system of interrelated thermal convection
equations and equations of motion of the solid continents.
This model [Trubitsyn and Rykov, 1995] reproduces the
general laws governing the formation and disintegration of
Pangea. Following the disintegration of Pangea, structures
are formed similar to the Atlantic and Pacific Oceans,
subduction zones being formed at the oceanic margins of the
Pacific, one with an almost vertical subsidence (similar to
Kurile-Kamchatkan zone) and the other with a very gently
sloping subsidence (similar to the South-American zone). In
the model with a different initial arrangement of the
continents [Rykov and Trubitsyn, 1996b], there formed,
after
the disintegration of the supercontinent, a structure of two
coupled continents similar to North and South Americas.
Trubitsyn and Rykov [1997] were the first to explain
the
causes of the inclined subsidence of the oceanic lithosphere
under the overthrusting continent. They carried out a self-consistent
numerical modeling of convection in the upper
mantle of variable viscosity (at a not very high Rayleigh
number of Ra = 10
4 ) interacting with a moving continent.
The continent was modeled by a thick solid plate. Cases were
analyzed where the plate could drift in the mantle either
freely or with a specified velocity. It turned out that as
it approached the descending, cold mantle convection flow,
the continent deflected the latter, forming structures
similar to inclined subduction zones. The inclination angle
of the descending mantle convection flow with respect to the
horizontal increased with the velocity of the overriding
continent.
In their 2-D model, Trubitsyn and Rykov [1998b] presented
in detail the mathematical formulation of the problem and
the method to solve it. They analyzed a convection model,
more like the actual Earth, at a Rayleigh number of Ra = 10
6 on a
200 by 80 grid with a thin continent with a
thickness of
d = 90 km and a horizontal dimension of
l = 6 thous. km.
Calculations were made for a long-term evolution
of the mantle-continent system. Comparison between the
evolution of nonstationary convection in the mantle without
and with the continent at the same points in time showed the
moving continent to have a drastic effect on the structure
of mantle convection.
The same authors presented the results of a series of
numerical experiments conducted on 2- and 3-D models
[Trubitsyn and Rykov, 1998c], which revealed four specific
thermal convection features manifest in the global tectonics
of the Earth. Consideration was given to the mechanisms
governing the origin and circulation of the oceanic
lithosphere, as well as the generation and ascent of plumes,
the character of the incomplete mass exchange between the
upper and lower mantle, and the effect of drifting
continents on mantle convection, causing in particular the
difference between the continental and oceanic lithosphere.
They also formulated [Trubitsyn and Rykov, 1998a] a new
concept of global geodynamic processes, namely, tectonics of
drifting continents and oceanic lithospheric plates.
Lithospheric plate tectonics explains the processes
occurring beneath the oceans and drifting continent
tectonics, those taking place beneath the continents. This
work presents for the first time a numerical model of
convection in a spherical 3-D mantle with drifting
continents.
2. Model
As noted in the introduction, over the past few years the
authors have been publishing the results of modeling mantle
convection interacting with drifting continents. It has
turned out that it is exactly this interaction that causes
global changes in mantle convection. In actual fact, the
continents are the regulators of the global geodynamic
processes in the Earth [Trubitsyn and Rykov, 1998a].
The
question may arise as to why no other author has so far
published in the literature any calculation results for 3-D
mantle convection models with drifting continents, though
this problem arose ten years ago. The reason is probably
that the American and European geodynamics scientists
believed the continents to be less viscous than the oceanic
lithospheric plates. But in that case, the continents should
deform and get crushed faster than the oceanic plates, and
this is not the case. The present authors have proceeded
from the assumption that the oceanic lithosphere as a whole
consists of a set of plates and can deform and sink in the
mantle easier than an individual plate. Therefore, as a
first approximation, the authors have taken a model of
absolutely rigid continents interacting with a mantle. The
viscosity of the mantle being dependent on temperature and
pressure, the low-viscosity asthenosphere and high-viscosity
oceanic and continental lithosphere are not specified but
arise in a self-consistent fashion as a result of solution
of equations. Modeling the continents by thick solid slabs
and explicitly using natural variables (mantle convection
flow and continental drift velocities) have enabled us to
describe for the first time not only the translational
motion of the continents, but also their rotation in space.
So, the model reduces to the following. A globe is
considered whose central part is occupied by a liquid core
and the outer shell comprises a viscous silicate mantle. The
boundary between the core and the mantle is taken to be
undeformable, free from adhesion, and at a fixed
temperature. It is assumed for simplicity that the mantle is
heated from below and develops thermal convection. Immersed
into the mantle are solid drifting continents. Specified on
the mantle surface not occupied by the continents are the
free-slippage conditions for the velocities and fixed zero
temperature. On the entire surface of each continent there
are specified the complete adherence condition for mantle
convection flows, as well as the temperature and heat flow
continuity conditions. Thus, a continent moves under the
action of the total force of viscous coupling with the
mantle convection flows at the end faces and the foot of the
continent. In cases where the continents collide, an
effective repelling force is introduced at all the points of
contact between them. This force at each instant of time is
selected such that the continents neither intersect, nor
bounce back off each other to a distance less than the
spatial mesh width of the computational grid.
3. Mantle Convection Equations
Thermal convection in a viscous mantle is defined by the
convection flow velocity vector distribution
Vi(x, y, z),
temperature distribution
T(x, y, z), and pressure
distribution
p(x, y, z). In the Boussinesq
approximation, these unknown functions are found by solving
the set of three equations, namely, the momentum-, heat-,
and mass-transfer equations
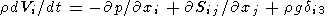 | (1) |
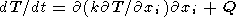 | (2) |
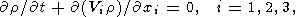 | (3) |
where
r is the density of the mantle,
gi is the
acceleration due to gravity,
T is the temperature reckoned
from the adiabatic distribution,
k is the thermal
conductivity coefficient,
Q is the thermometric density of
the heat sources,
dij is the Kronecker symbol
equal
to unity at
i = j and zero at
i j, and
Sij is the
viscous stress deviation tensor
[Landau and Lifshits, 1986], given by
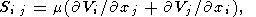 | (4) |
where
m is the kinematic viscosity.
The relative magnitude of the inertial terms on the left-hand
side of equation (2) for the momentum transfer in a
viscous fluid is of the order of
kr/m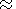 10-23 with respect to the terms on the
right-hand sides of the
equations, and so these inertial terms can be disregarded.
In the Boussinesq approximation, we put
r = r0(1
- aT) in the last buoyancy term of equation
(1) and
r = r0
in all the remaining terms of equations
(1)-(3). We will reckon pressure from its hydrostatic
distribution
p(z) subject to the condition
10-23 with respect to the terms on the
right-hand sides of the
equations, and so these inertial terms can be disregarded.
In the Boussinesq approximation, we put
r = r0(1
- aT) in the last buoyancy term of equation
(1) and
r = r0
in all the remaining terms of equations
(1)-(3). We will reckon pressure from its hydrostatic
distribution
p(z) subject to the condition
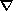 p0 = -r0g.
We introduce dimensionless
variables, taking the mantle thickness
D as a unit of
measurement for length,
D/k for velocity,
D2/k for
time,
T0 for temperature,
m0 for viscosity,
m0 k/D2 for
pressure and stress, and
kT0/D2 for
heat source density.
p0 = -r0g.
We introduce dimensionless
variables, taking the mantle thickness
D as a unit of
measurement for length,
D/k for velocity,
D2/k for
time,
T0 for temperature,
m0 for viscosity,
m0 k/D2 for
pressure and stress, and
kT0/D2 for
heat source density.
In these variables, convection equations (1)-(3) assume
the form
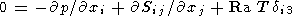 | (5) |
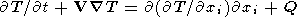 | (6) |
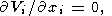 | (7) |
where Ra is the Rayleigh number given by
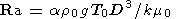 | (8) |
4. Equations of Motion of Freely Drifting Continent
The velocity components
u(u, v, w) of any point of a
solid continent may be represented in the form
[Landau and Lifshits, 1965]
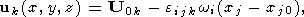 | (9) |
where
U0k = (u0, v0, w0)
is the instantaneous
velocity vector of the center of gravity of the continent,
wi = (wx,
wy, wz)
is the
instantaneous angular velocity vector in rotation about this
center of gravity,
xi are the coordinates of an arbitrary
point of the continent,
xi0 are the coordinates of the
instantaneous center of gravity of the continent, and
eijk is the Levi-Civita symbol
equal to zero when
any two of the subscripts coincide, 1 in the case of even
transposition of the subscripts with respect to 123, and
- 1
in the case of odd transposition.
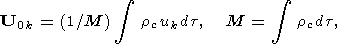 | (10) |
where
rc is the density distribution
in the continent,
dt is the volume element, and
M is the mass of the
continent.
In the generals case, the Euler equations for the motion
of a solid have the form [Landau and Lifshits, 1965]
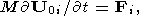 | (11) |
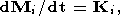 | (12) |
where
Fi is the external force and
Mi is the moment of
momentum of the solid.
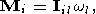 | (13) |
where
Iik is the inertia tensor of the solid expressed as
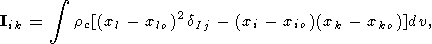 | (14) |
Ki is the total force moment made up of the moments
ki of the forces
fj acting upon the individual elements of
the solid, these moments being given by
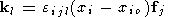 | (15) |
The continent is acted upon by the gravity force applied
to its center of gravity and by the forces of interaction
with the viscous mantle, applied to the surface elements of
the immersed portion of the continent. Under the effect of
these forces the continent drifts in the mantle, moving over
its surface and rotating about the vertical axis. As the
pressure and velocity of the mantle convection flows vary in
time and space, both the vertical velocity
w0 of the
center of gravity of the continent and its rotation
velocities
wx and
wy about the instantaneous
horizontal axes
x and
y are in the general case other than
zero. Continents can sink (when they are over descending
mantle convection flows), together with and relative to the
mantle surface, and rise (at ascending flow locations), the
subsidence and rise of the opposite ends of the continents
being not necessarily equal.
In the subsequent discussion we only consider the
horizontal motions of the center of gravity of the continent
and the rotation of the latter about its vertical axis,
neglecting all the other small effects and putting
w0 = 0 and
wx = wy
= 0. Inasmuch as the gravity
force is counterbalanced by the buoyant force, the external
force acting on the continent is reduced to the force of
viscous coupling with the mantle, the pressure
p being
reckoned from the hydrostatically equilibrium distribution
p0(z):
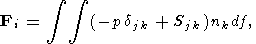 | (16) |
where
df is the magnitude of the surface element of the
solid continent and
nj is the unit vector of the external
normal to the surface of the continent. The integral is
taken over the entire surface of the portion of the
continent of arbitrary-shape immersed into the mantle.
Thus, the Euler equations for the horizontal motion of a
solid continent of arbitrary shape and its rotation about
the instantaneous vertical axis are reduced to the following
system of three equations [Landau and Lifshits, 1965]:
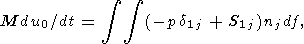 | (17) |
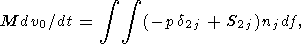 | (18) |
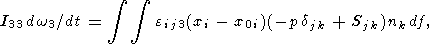 | (19) |
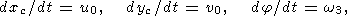 | (20) |
where
xc(t) and
yc(t) are the coordinates of the
center of gravity of the continent and
j is the
angle of rotation of the continent.
In the particular case of horizontal motion of infinitely
thin solid continents, the viscous force only acts at the
foot of the continent, for which
nk = (0, 0, -1). In that
case, the Euler equations are simplified:
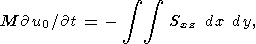 | (21) |
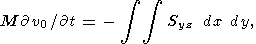 | (22) |
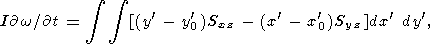 | (23) |
where
I is the moment of inertia of the continent about the
axis
z passing through its center
of gravity and
calculated in the moving coordinate system with the axes
x
passing through its center
of gravity and
calculated in the moving coordinate system with the axes
x and
y
and
y directed along the principal
axes of inertia of the
continent:
directed along the principal
axes of inertia of the
continent:
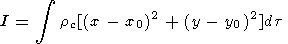 | (24) |
It follows from dimensional relations that the magnitude
of the inertial terms on the left-hand side of Euler
equations (17)-(19) for the motion of continents is, as in
the case of equation (1) for momentum transfer in a viscous
fluid, of the order of
kr/m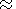 10-23.
10-23.
With the inertial terms being omitted, The Euler equations
for the motion of continents yield the following six
relations for finding the coordinates
xc(t) and
yc(t) of the center of gravity of the continent,
its angle of
rotation
j, and velocities
u0(t),
v0(t), and
w3(t):
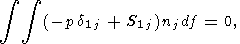 | (25) |
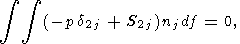 | (26) |
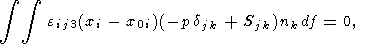 | (27) |
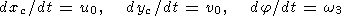 | (28) |
The equation for the distribution of the temperature
Tc inside the solid continent in the initial fixed coordinate
system reduces to the heat-transfer equation involving
advective heat transfer at a rate satisfying relation (9)
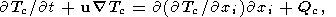 | (29) |
where
Qc is the density of heat sources inside the
continent.
5. Boundary Conditions
Mantle convection equations (1)-(3) and equations (17)-(19)
for the motion of the continent and equation (29) for heat
transfer therein are interrelated through the intermediary
of boundary conditions.
As noted, zero flow and zero slippage conditions (i.e.,
zero normal fluid velocity component and zero tangential
viscous force components) are specified at the bottom and
side boundaries of the computational region:
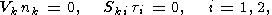 | (30) |
where
nk is the unit vector normal to the given surface
and
ti are the unit vectors tangent
to it.
Specified at the boundaries of the solid mobile continent,
all over its portion immersed into the mantle, is the zero
flow and adherence condition, i.e., the equality between the
mantle convection flow and continent drift velocities,
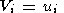 | (31) |
The temperature at the lower boundary of the region is
fixed at
T = 1. At the side boundaries there is specified
the zero heat flow condition
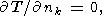 | (32) |
where
nk is the unit vector normal to the lateral surface
of the region.
The temperature of the mantle on the top, free surface is
equal to zero
(T = 0) but only in the oceanic region
outside the continent.
On the surface of the immersed portion of the continent
there are specified the mantle-continent temperature and
heat flow continuity conditions
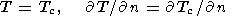 | (33) |
The temperature on the top surface of the continent is
taken to be zero:
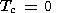 | (34) |
Thus, the mathematical problem reduces to the following.
There are three unknown functions of coordinates and time
for mantle convection, namely, the mantle convection flow
velocity vector distribution
Vi(x, y, z, t), temperature
distribution
T(x, y, z, t), and pressure distribution
p(x, y, z, t), and also four unknown functions
of time for
the motion of continents as a whole, namely, the two
components of the instantaneous translational velocity of
the center of gravity, i.e.,
u0(t) and
v0(t), one
component of the instantaneous angular velocity of the
continent about its center of gravity,
w(t), and the
temperature distribution in the continent,
Tc(x, y, z, t).
To find these unknowns, there is a system of connected
equations, namely, three differential convection equations
(1)-(3), three integral relations (25)-(27) whereto the
Euler equations of motion have reduced, and continental heat-transfer
equation (29). Given the position of the continent
and its velocities
u0(t),
v0(t), and
w(t), one
can find its position at the next instant of time. Boundary
conditions (30)-(34) serve to find the integration constants
for the differential equations.
The difference between the present problem with a freely
drifting continent and the well-known problem with a fixed
continent is that the boundary conditions for the convection
flow velocities and temperature at the mantle-continent
boundary are specified at each given instant of time at the
location of the drifting continent whose velocity and
position are not known beforehand, but are determined by
solving a set of connected differential equations.
If there are a number of continents, equations of motion
(25)-(27) and temperature equation (29) are written down for
each continent. Besides, in the case where solid continents
collide, the condition is specified for the impossibility of
their penetration into each other. To this end, at the
instant when the colliding continents come into contact at
some point a repelling force is applied at this point to
each continent, in addition to the forces of viscous
coupling with the mantle, the force being directed opposite
to the relative velocity of the continents. The algorithm
for computing these forces is described below.
6. Numerical Technique
6.1. Method of Joining Two Regions and Through
Computation
Method
To numerically solve the set of thermal convection equations
in the case of drifting continents, use can be made of two
principally different methods. In the method of two regions,
heat- and mass-transfer equations are solved at each time
step separately for the mantle outside of the continent and
for the continent, and the solutions obtained are then
joined so as to satisfy the boundary conditions on the
continent's portion immersed into the mantle. In the through
computation method, analyzed at each time step at the given
position of the continent is its own unified computational
region, the jump of the parameters characterizing the
different properties of the materials of the mantle and
continents being explicitly allowed for on the surface of
the latter. The numerical algorithm procedure in the through
computation method is simpler, but it is necessary in that
case to smooth out the jumps of the functions by replacing
at each time step the solid continent by a high-viscosity
region.
6.2. Algorithm for Computing Forces of Interaction Between
Thermal Convection and a Drifting Continent
In the general case, the algorithm for the numerical
solution of the set of thermal convection equations in the
case of drifting continent reduces to the following. Let
there be given at the instant
t1 the convective flow
velocities, the field of the temperatures
T(t1) and
pressures
p(t1) in the mantle, as well as the position
x1(t1),
y1(t1) of the continent and its velocities
u0(t1),
v0(t1), and
w(t1). We need to find
the solution of the set of equations (1)-(5), (25)-(27), and
(29) at the next instant of time,
t2 = t1 + Dt.
The new position of the continent,
x1(t2),
y1(t2), at the instant
t2 can simply be found from
equation (28):
x1(t2) = x1(t1)
+ u0(t1)Dt,
y1(t2) = y1(t1)
+ v0(t1)Dt.
If the new velocities
u0(t2),
v0(t2), and
w(t2) of the continent in this
position were also
known, it would then be possible again to solve thermal
convection equations (1)-(5) subject to boundary conditions
(32)-(34) for temperature and (30)-(31) for velocities,
corresponding to the new position of the continent, and find
the mantle convection flow velocities
Vx(t2),
Vy(t2), and
Vz(t2), the temperature
T(t2), and
pressure
p(t2). But the difficulty of the problem is
precisely the fact that it is exactly these velocities of
the continent,
u0(t2),
v0(t2), and
w(t2),
that are unknown. They must be such as to make the newly
found mantle convection flow velocities
Vx(t2),
Vy(t2), and
Vz(t2) corresponding to these new
velocities
u0(t2),
v0(t2), and
w(t2) satisfy equations of motion
(25)-(27) of the continent as
well. It is therefore necessary to use some iteration
technique to find these velocities of the continent. One
can, in principle, use a certain scheme to search for the
continent velocity values, computing convection flow
velocity fields and evaluating integrals (25)-(27), until
such values of the velocities
u0(t2),
v0(t2), and
w(t2) are found as make the
right-hand sides of
relations (25)-(27) differ from zero by an amount less than
the preset number
e corresponding to the prescribed
accuracy of computation. Since the right-hand side of
relations (25)-(27) corresponds, in physical sense, to the
forces and moment of force acting on the continent, then
e>0 if the selected continent velocities
u0(t2),
v0(t2), and
w(t2) are
underestimated and
e<0 if they are overestimated.
6.3. Algorithm for Computing Repelling Forces for Colliding
Continents
As noted earlier, when computing the motion of continents,
the condition is specified for the impossibility of their
mutual penetration. This condition is implemented by the
following algorithm. In computing the motion of the
continents, the condition for preventing their overlapping
is being constantly checked. If at some instant
t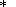 1 some
point of one continent falls in the region of another
continent, the computational procedure goes back to the
previous instant of time,
t
1 some
point of one continent falls in the region of another
continent, the computational procedure goes back to the
previous instant of time,
t 2 = t
2 = t 1 - Dt,
and the computation starts again at that instant with a
continent repelling force being added to the right-hand side
of equations of motion (27)-(29). The direction, magnitude,
and point of application of this force are chosen as
follows. The first to be found are the average velocities
U1 and
U2 of the points of each continent that have
found themselves in the continent overlapping region. Next
the difference between these velocities is found. The point
of application of the repelling forces to each continent is
taken to be the center of the overlapping region. The
direction of the continent repelling forces is taken to be
opposite to that of the relative velocity of one continent
with respect to the other. The magnitude of the forces is
selected in an iterative manner. At first, some value of the
repelling force is taken, and next the systems of heat
convection equations (1)-(5), heat-transfer equations (29),
and equations of motion (25)-(27) are solved with due regard
for this additional force. If in the course of the time
interval
Dt the continents part to a distance
greater than the mesh width of the computational grid, the
magnitude of the repelling force selected is reduced. While
the continents stay in contact their translational and
rotational velocities change substantially in comparison
with freely drifting continents.
1 - Dt,
and the computation starts again at that instant with a
continent repelling force being added to the right-hand side
of equations of motion (27)-(29). The direction, magnitude,
and point of application of this force are chosen as
follows. The first to be found are the average velocities
U1 and
U2 of the points of each continent that have
found themselves in the continent overlapping region. Next
the difference between these velocities is found. The point
of application of the repelling forces to each continent is
taken to be the center of the overlapping region. The
direction of the continent repelling forces is taken to be
opposite to that of the relative velocity of one continent
with respect to the other. The magnitude of the forces is
selected in an iterative manner. At first, some value of the
repelling force is taken, and next the systems of heat
convection equations (1)-(5), heat-transfer equations (29),
and equations of motion (25)-(27) are solved with due regard
for this additional force. If in the course of the time
interval
Dt the continents part to a distance
greater than the mesh width of the computational grid, the
magnitude of the repelling force selected is reduced. While
the continents stay in contact their translational and
rotational velocities change substantially in comparison
with freely drifting continents.
6.4. Numerical Solution of Convection Differential Equations
The system of thermal convection equations with drifting
continents were solved by the finite-difference technique
[Rykov and Trubitsyn, 1996b]. When numerically solving
heat-transfer equations (6), (29), use was made of the Zalesak
flux-corrected transport technique [Zalesak, 1979]. Velocity
and pressure equations (5), (7), (25)-(28) were reduced to
elliptic equations with variable coefficients (generalized
Poisson equations). These equations were solved by means of
the alternating triangular technique in the three-layer
modification, the iterative parameters being chosen by the
conjugate gradient method [Samarskii and Nikolaev, 1978].
7. Computation Results
Computations were carried out on 3-D spherical models.
Therefore, the general equations discussed above were
converted to a spherical coordinate system for the mantle
convection flow velocities
Vr(r, q, f, t),
Vq(r, q,
f, t), and
Vf(r, q,
f, t),
temperature
T(r, q, f,
t), the velocities of
the centers of gravity of the
continents,
uq (r, q,
f, t) and
uf (r, q,
f, t), and their solid-body
rotation with the angular velocities
dj/dt in the
local instantaneous coordinate system.
To analyze the interaction between drifting continents and
mantle convection flows, two models were considered: Model 1
with a single freely drifting continent and a weak thermal
convection in the mantle at a Rayleigh number of Ra = 104
and Model 2 with five drifting continents and an intense
thermal convection at a Rayleigh number of Ra = 106. A
fixed temperature at the mantle-core boundary and zero
temperature at the surface were taken as the boundary
conditions for both models. The initial state was taken to
be a viscous convection-free mantle with its temperature
distribution corresponding to a steady-state conductive heat
flow. A small arbitrary temperature perturbation was then
introduced, and the temperature and convection flow velocity
evolution was calculated by the mantle convection equations.
With time a quasistationary thermal convection was
established in the mantle, its structure being almost
independent of the initial perturbation. Thereupon
continents were placed into the mantle, and the subsequent
evolution of the mantle-continent system was computed by
solving the system of connected mantle convection equations
and equations of motion of the continents.
 As noted earlier, the mantle convection structure in
dimensionless variables at a constant viscosity depends on a
single parameter - the Rayleigh number Ra. For the spherical
Earth, the Rayleigh number is estimated by various authors
at around 106. At a lower intensity, convection in the
mantle is less chaotic, and the motion of continents is more
regular. To reveal the drift specifics of the continents, we
first computed Model 1.
Figure 1 presents the radial
distributions of the above-adiabatic temperature,
T(r) ,
and the Nusselt number Nu = Nu
(r) of the dimensionless heat
flow, established in the course of convection in the mantle
at a Rayleigh number of Ra = 104
As noted earlier, the mantle convection structure in
dimensionless variables at a constant viscosity depends on a
single parameter - the Rayleigh number Ra. For the spherical
Earth, the Rayleigh number is estimated by various authors
at around 106. At a lower intensity, convection in the
mantle is less chaotic, and the motion of continents is more
regular. To reveal the drift specifics of the continents, we
first computed Model 1.
Figure 1 presents the radial
distributions of the above-adiabatic temperature,
T(r) ,
and the Nusselt number Nu = Nu
(r) of the dimensionless heat
flow, established in the course of convection in the mantle
at a Rayleigh number of Ra = 104
 .
Shown in Figure 2
is the
temperature distribution
T(r, q) in the zero-longitude
cross section. The dimensionless temperature
values are in the interval from zero (on the surface) to
unity (at the mantle-core boundary). The correspondence
between the temperature values and the color scale is
indicated at the left of the figure. The liquid core of the
Earth is colored dark-red. The arrows indicate the direction
and relative magnitude of mantle convection flows. The
dimensionless velocity scale is also given at the left of
the figure. Indicated at the upper left of the figure is the
dimensionless instant of time at which convection reached
the steady state. The continent, colored red on the right-
hand side of the sphere, is placed into the mantle at that
instant.
.
Shown in Figure 2
is the
temperature distribution
T(r, q) in the zero-longitude
cross section. The dimensionless temperature
values are in the interval from zero (on the surface) to
unity (at the mantle-core boundary). The correspondence
between the temperature values and the color scale is
indicated at the left of the figure. The liquid core of the
Earth is colored dark-red. The arrows indicate the direction
and relative magnitude of mantle convection flows. The
dimensionless velocity scale is also given at the left of
the figure. Indicated at the upper left of the figure is the
dimensionless instant of time at which convection reached
the steady state. The continent, colored red on the right-
hand side of the sphere, is placed into the mantle at that
instant.
 Figure 3 (7 frames) presents the computation results
for the evolution of the mantle-continent system. For the
sake of definiteness, the shape of the continent and its
position are chosen to be similar to modern Africa. But the
structure of mantle convection cannot correspond to the
modern Earth, because the state of mantle convection at the
moment the continent is placed into the mantle is selected
arbitrarily. Thus, the model under consideration only serves
to reveal the principal possibility of and the laws
governing the drift of the continent. The distribution of
the computed dimensionless heat flow (the Nusselt number)
over the Earth's surface is depicted in color. Recall that
the temperature at the surface of the continent and the
surface of the free portion of the mantle is the same and
equals zero in the dimensionless units adopted. The entire
surface of the Earth in these figures is shown in developed
projection.
Figure 3 (7 frames) presents the computation results
for the evolution of the mantle-continent system. For the
sake of definiteness, the shape of the continent and its
position are chosen to be similar to modern Africa. But the
structure of mantle convection cannot correspond to the
modern Earth, because the state of mantle convection at the
moment the continent is placed into the mantle is selected
arbitrarily. Thus, the model under consideration only serves
to reveal the principal possibility of and the laws
governing the drift of the continent. The distribution of
the computed dimensionless heat flow (the Nusselt number)
over the Earth's surface is depicted in color. Recall that
the temperature at the surface of the continent and the
surface of the free portion of the mantle is the same and
equals zero in the dimensionless units adopted. The entire
surface of the Earth in these figures is shown in developed
projection.
 A more detailed continental drift evolution in Model 1 is
given in the online version of this paper in the form of a film
(anim01). This film contains 55 frames.
As can be seen from these pictures, when convection is weak,
there form in the mantle but a few ascending and descending
convection flows, the descending flows being practically
united into a single system. The continent if first pulled
into the site of one of the descending flows. But since the
shape and size of the continent fail to coincide with those
of the descending flow spot on the Earth's surface, this
position of the continent proves unstable. As the constant-viscosity
model under consideration disregards the oceanic
lithosphere and contains but a single continent, the motion
of the latter turns out to be free. The continent starts
drifting along the system of united descending mantle
convection flows. Because the continent impedes the outflow
of heat from the mantle, the mantle starts heating, provided
the continent is stationary and large enough, so that in
200-400 million years there develops an ascending, hot
convection flow [Trubitsyn and Bobrov, 1996].
If the continent drifts rapidly, no hot ascending mantle convection
flow has enough time to develop beneath it. But as can be
seen from the film, when the drift is
slowed down, an ascending flow can partially arise behind
the continent.
A more detailed continental drift evolution in Model 1 is
given in the online version of this paper in the form of a film
(anim01). This film contains 55 frames.
As can be seen from these pictures, when convection is weak,
there form in the mantle but a few ascending and descending
convection flows, the descending flows being practically
united into a single system. The continent if first pulled
into the site of one of the descending flows. But since the
shape and size of the continent fail to coincide with those
of the descending flow spot on the Earth's surface, this
position of the continent proves unstable. As the constant-viscosity
model under consideration disregards the oceanic
lithosphere and contains but a single continent, the motion
of the latter turns out to be free. The continent starts
drifting along the system of united descending mantle
convection flows. Because the continent impedes the outflow
of heat from the mantle, the mantle starts heating, provided
the continent is stationary and large enough, so that in
200-400 million years there develops an ascending, hot
convection flow [Trubitsyn and Bobrov, 1996].
If the continent drifts rapidly, no hot ascending mantle convection
flow has enough time to develop beneath it. But as can be
seen from the film, when the drift is
slowed down, an ascending flow can partially arise behind
the continent.


 Figures 4, 5, and 6 present the computation results
for the evolution of mantle convection with five continents
at a Rayleigh number of Ra = 106.
Shown in Figure 4 is the
computed radial distribution of temperature (violet curve)
and heat flow (red curve) in the mantle. Figure 5 (4 frames)
presents the computation results for the evolution of the
mantle-continent system in Model 2. As distinct from Model 1,
these figures show the Earth's hemisphere as seen from
the observation point with a latitude of
90o and longitude
of
0o. The initial position and shape of the continents are
taken to be similar to Africa, North and South Americas,
Australia, and Eurasia. The shape of each continent is
described approximately on the basis of 12 angular points of
the contour. The structure of convection at the moment the
continents are placed into the mantle being arbitrary, the
model computed does not aim to trace the drift of the
continents on the actual Earth, but merely reveals the
principal specifics of the drift of the continents,
particularly the possibility of their uniting into
supercontinents and subsequent parting.
Figures 4, 5, and 6 present the computation results
for the evolution of mantle convection with five continents
at a Rayleigh number of Ra = 106.
Shown in Figure 4 is the
computed radial distribution of temperature (violet curve)
and heat flow (red curve) in the mantle. Figure 5 (4 frames)
presents the computation results for the evolution of the
mantle-continent system in Model 2. As distinct from Model 1,
these figures show the Earth's hemisphere as seen from
the observation point with a latitude of
90o and longitude
of
0o. The initial position and shape of the continents are
taken to be similar to Africa, North and South Americas,
Australia, and Eurasia. The shape of each continent is
described approximately on the basis of 12 angular points of
the contour. The structure of convection at the moment the
continents are placed into the mantle being arbitrary, the
model computed does not aim to trace the drift of the
continents on the actual Earth, but merely reveals the
principal specifics of the drift of the continents,
particularly the possibility of their uniting into
supercontinents and subsequent parting.
As seen from Figure 5, three continents
(Africa, Eurasia, and North America) start drifting
northwards. The other two continents (Australia and South
America) drift southwards.
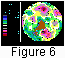
Figure 6 (11 frames) illustrates the further evolution
of the mantle-continent system. Insofar as the continents by
that instant have gone to the other Earth's hemisphere,
these figures show the view of the globe as seen from the
point with the coordinates 45o S and 210o E. It can be seen
that at the instant of dimensionless time
t = 14.0298 three
continents (South America, Eurasia, and Australia) unite
into a supercontinent. At the instant
t = 14.03296 all the
five continents unite into a single supercontinent - Pangea.
As heat is accumulated beneath Pangea, the mantle material
at that spot becomes lighter in weight. The descending
convection flow changes to an ascending one which splits
Pangea apart by the instant of dimensionless time
t = 14.0355.
Following the breakup of Pangea, there remains for
a long time at its location a system of hot ascending mantle
convection flows similar to the giant hot anomaly beneath
the Pacific Ocean.
 A more detailed drift evolution of the five continents in
Model 2 in the online version of this paper in the form of a film
(anim02). This film
contains 16 frames for the initial stage of evolution viewed
from one side and 85 frames for the evolution stage
involving the uniting of three and five continents.
A more detailed drift evolution of the five continents in
Model 2 in the online version of this paper in the form of a film
(anim02). This film
contains 16 frames for the initial stage of evolution viewed
from one side and 85 frames for the evolution stage
involving the uniting of three and five continents.
8. Conclusion
As stated at the 1998 International Gordon Conference
(Gordon Research Conference - Interior of the Earth, June 28 - July 3, 1998,
Boston, USA), the two most important
problems of geoscience still to be solved are the
explanation of the continent uniting and parting events that
took place repeatedly in the Earth's history and the
explanation of the nature of the continental lithosphere,
its formation and evolution.
The solution of these problems will actually be the next
important stage in the development of the concept of the
structure of the Earth and of the processes occurring
therein. Plate tectonics has only explained the nature of
the oceanic lithosphere, the continents being merely
regarded as passively drifting inhomogeneities frozen into
oceanic plates. As the oceanic lithospheric plates have
existed for no more than 200 million years, plate tectonics
cannot in principle explain global geological processes
lasting for billions of years, particularly the causes of
formation and breakup of supercontinents. Obviously the
continental lithosphere which is older than the oceanic
plates could not arise but for the continents. The
properties and evolution of the continental lithosphere must
be governed by the long-lasting mobile continents.
A new approach to global tectonics was advanced by
Trubitsyn and Rykov [1995, 1997,
1998a, 1998b, 1998c].
Based
on detailed numerical experiments on 2- and 3-D models in
orthogonal coordinates, they have demonstrated that the
continents are not passive inclusions in lithospheric
plates, but, on the contrary, are the chief regulators of
the entire global tectonics of the Earth. It were precisely
the continents that came into existence more than three
billion years ago that formed the continental lithosphere
and determined its properties different from those of the
oceanic lithosphere.
Presented for the first time in this work is a 3-D
spherical model of mantle convection interacting with
several drifting continents. The adherence condition on the
surface of the mantle-immersed portion of the continents
introduces the mechanical interaction between the mantle and
continents. The temperature and heat flow continuity
conditions on the mantle-continent boundaries introduces the
thermal mantle-continent interaction. The continents
interact with one another upon direct collision and through
the intermediary of the mantle, thus changing its structure.
The solution of the system of connected mass-, heat-, and
momentum-transfer equations for the viscous mantle and Euler
equations for the solid continents has for the first time
allowed the evolution of the mantle-continent system to be
described in a self-consistent fashion on a 3-D model.
Thanks to the sphericity of the model (devoid of side
boundaries), it has proved possible to trace a very long
drift evolution of the continents and describe for the first
time both the formation and breakup of supercontinents.
It should be noted that that the present model only proves
the principal possibility of formation and breakup of
supercontinents without any direct relation to the actual
Earth. This is due to the fact that the structure of mantle
convection at the instant the continents were placed into
the mantle was taken on the basis of model computations for
the establishment of convection, whereas the actual mantle
convection structure resulted from a great number of
complicating processes, such as the differentiation of
matter, redistribution of heat sources, substantial changes
in viscosity, and so on.
However, the solution of the problem proves possible if
use is made of seismic tomography data. Converting the
distribution of seismic wave velocities yields the modern
instantaneous temperature distribution in the Earth. Solving
the system of convection equations with drifting continents
will therefore provide the possibility of determining the
mantle convection flow velocities which materially depend on
adherence to the solid continents. What is more, the
mathematical apparatus developed by the authors makes it
possible to compute the drift velocities of the continents
themselves, heat flow distribution, relief, gravity field,
and stress distribution over the entire Earth. With the
model parameters being optimized so as to make the
computation results agree with the entire mass of
observation data available, it will be possible to construct
a complete geodynamic model of the Earth. This model will
enable one to observe on the computer the processes
occurring in the Earth's interior, specifically those giving
rise to mineral deposits and altering the general stress
field.
References
Bobrov, A. M., and Trubitsyn, V. P., Times of rebuilding of
mantle flows beneath continents, Izvestiya, Physics of the Solid Earth, 31,
551-559, 1996.
Christensen, U. R., A numerical model of coupled subcontinental
and oceanic convection, Tectonophysics, 95, 1-23, 1983.
Christensen, U. R., Convection with pressure- and
temperature-dependent non-Newtonian rheology, Geophys. J. Astr. Soc., 77,
343-384, 1984.
Christensen, U. R., Heat transfer by variable viscosity
convection. II. Pressure influence, non-Newtonian rheology
and decaying heat sources, Phys. Earth Planet. Inter., 37,
183-205, 1985.
Christensen, U. R., and Yuen, D. A., The interaction of a
subducting lithospheric slab with a chemical or phase
boundary, J. Geophys. Res., 89, 4389-4402, 1984.
Doin, M.-P., Fleitout, L., and Christensen, U., Mantle
convection and stability of depleted and undepleted
continental lithosphere, J. Geophys. Res., 102,
2771-2787, 1997.
Fukao, Y., Maruyama, S., Obayashi, M., and Inoue, H.,
Geological implication of the whole mantle
P -wave
tomography, J. Geol. Soc. Japan, 100, 4-23, 1994.
Glatzmaier, G. A., Numerical simulation of mantle
convection: Time-dependent three-dimensional, compressible,
spherical shell, Geophys. Astrophys. Fluid Dyn., 43,
223-264, 1988.
Guillou, L., and Jaupart, C., On the effect of continents
on mantle convection, J. Geophys. Res., 100,
24,217-24,238, 1995.
Gurnis, M., Large-scale mantle convection and aggregation
and dispersal of supercontinents, Nature, 332,
696-699, 1988.
Gurnis, M., and Zhong, S., Generation of long wavelength
heterogeneity in the mantle dynamics interaction between
plates and convection, Geophys. Res. Lett., 18,
581-584, 1991.
Jacoby, W. R., and Schmeling, H., On the effects of the
lithosphere on mantle convection and evolution, Phys. Earth Planet. Int., 9,
305-319, 1982.
Landau, L. D., and Lifshits, E. M., Hydrodynamics,
Nauka, Moscow, 1986.
Landau, L. D., and Lifshits, E. M., Mechanics, Nauka, Moscow, 1965.
Lenardic, A., and Kaula, W. M., Tectonic plates,
D
 thermal
structure, and the nature of mantle plumes, J. Geophys. Res., 99, 15,697-15,708,
1994.
thermal
structure, and the nature of mantle plumes, J. Geophys. Res., 99, 15,697-15,708,
1994.
Lowman, J. P., and Jarvis, J. T., Mantle convection flow
reversals due to continental collisions, Geophys. Res. Lett., 20, 2091-2094,
1993.
Lowman, J. P., and Jarvis, J. T., Mantle convection models of
continental collision and breakup incorporating finite
thickness plates, Phys. Earth Planet. Inter., 88, 53068, 1995.
Lowman, J., and Jarvis, J. T., Continental collisions in
wide aspect ratio and high Rayleigh number two-dimensional
mantle convection models, J. Geophys. Res., 101, (B11),
25,485-25,497, 1996.
Lux, R. A., Davies, G. F., and Thomas, J. H., Moving
lithospheric plates and mantle convection, Geophys. J. R. Astron. Soc., 57,
209-228, 1979.
Machetel, P., and Weber, P., Intermittent layered
convection in a model mantle with an endothermic phase
change at 670 km, Nature, 350, 55-57, 1991.
Nakakuki, T., Yuen, D. A., and Honda, S., The interaction
of plumes with the transition zone under continents and
oceans, Earth Planet. Sci. Lett., 146, 379-391, 1997.
Parmentier, E. M., Sotin, C., and Travis, B. J., Turbulent 3-D
thermal convection in an infinite Prandtl number,
volumetrically heated fluid: Implication for mantle
dynamics, Geophys. J. Int., 116, 241-254, 1994.
Rykov, V. V., and Trubitsyn, V. P., Numerical technique for
calculation of three-dimensional mantle convection and
tectonics of continental plates, Computational Seismology and Geodynamics, 3,
17-22, 1996a.
Rykov, V. V., and Trubitsyn, V. P., 3-D model of mantle
convection incorporating moving continents, Computational Seismology and Geodynamics,
3, 23-32 1996b.
Samarskii, A. A., and Nikolaev, E. S., Methods of solving finite-difference equations,
Nauka, Moscow, 1978.
Solheim, L. P., and Peltier, W. R., Phase boundary
deflections at 660-km depth and episodically layered
isochemical convection in the mantle, J. Geophys. Res., 99,
15,861-15,875, 1994.
Tackley, P. J., Stevenson, D. J., Glatzmaier, G. A., and
Schubert, G., Effect of mantle phase transitions in three
dimension spherical model of convection in Earth's mantle,
J. Geophys. Res., 99, 15,877-15,901, 1994.
Trubitsyn, V. P., and Fradkov, A. S., Convection under
continents and oceans, Izvestiya, Physics of the Solid Earth, 21, (7), 491-498,
1985.
Trubitsyn, V. P., and Fradkov, A. S., Viscous retarding
forces of oceanic lithosphere, Fizika Zemli, (6), 3-16, 1986.
Trubitsyn, V. P., Bobrov, A. M., and Kubyshkin, V. V., Thermal
convection in the mantle due to horizontal and vertical
temperature gradients, Fizika Zemli, (5), 12-23, 1991.
Trubitsyn, V. P., Bobrov, A. M., and Kubyshkin, V. V., Influence
of continental lithosphere on structure of mantle thermal
convection, Izvestiya, Physics of the Solid Earth, 29,
377-385, 1993a.
Trubitsyn, V. P., Belavina, Yu. F., and Rykov, V. V., Thermal
and mechanical interaction of mantle and continental
lithosphere, Izvestiya, Physics of the Solid Earth, 29,
933-945, 1993b.
Trubitsyn, V. P., and Bobrov, A. M., Structure evolution of
mantle convection after breakup of supercontinent,
Izvestiya, Physics of the Solid Earth, 29, 768-778, 1994.
Trubitsyn, V. P., Belavina, Yu. F., and Rykov, V. V., Thermal
mantle convection in a varying viscosity mantle with a
finite-sized continental plate, Izvestiya, Physics of the Solid Earth, 30,
587-599, 1995.
Trubitsyn, V. P., and Bobrov, A. M., Thermal and mechanical interaction
of continents with the mantle, Computational Seismology and Geodynamics, 3,
33-41, 1996.
Trubitsyn, V. P., and Bobrov, A. M., Structure of mantle
convection beneath stationary continents, Computational Seismology and Geodynamics,
4, 42-53, 1997.
Trubitsyn, V. P., and Rykov, V. V., A 3-D numerical model of
the Wilson cycle, J. Geodynamics, 20, 63-75, 1995.
Trubitsyn, V. P., and Rykov, V.V., Mechanism of formation of
an inclined subduction zone, Izvestiya, Physics of the Solid Earth, 33, (6),
427-437, 1997.
Trubitsyn, V. P., and Rykov, V. V., Global tectonics of
drifting continents and oceanic lithospheric plates, Doklady RAN, 359, (1),
109-111, 1998a.
Trubitsyn, V. P., and Rykov, V. V., Self-consistent 2-D
mantle convection model with drifting continents, Russian J. Earth's Sciences
(electronic), 1, (1), 1998b,
http://eos.wdcb.rssi/ru/rjes98001/rje98001.html.
Trubitsyn, V. P., and Rykov, V. V., Mantle convection and
global tectonics of the Earth, Vestnik OGGGG RAN (electronic), 1, (3), 1998c,
http://www.scgis.ru/russian/cp1251/dgggms/1-98/main.html.
Turcotte, D. L., and Schubert G., Applications of Continuum Physics to Geological
Problems, New York: John Wiley & Sons, 1982.
Zalesak, S. T., Fully multidimensional flux-corrected
transport algorithms for fluids, J. Comp. Phys., 31,
335-361, 1979.
Zhong, S., and Gurnis, M., Dynamic feedback between a
continent-like raft and thermal convection, J. Geophys. Res., 98, 12,219-12,232,
1993.
Zhong, S., and Gurnis, M., Role of plates and temperature-
dependent viscosity in phase change dynamics,
J. Geophys. Res., 99, 15,903-15,917, 1994.
Load files for print and local use.
This document was generated by TeXWeb
(Win32, v.1.0) on April 4, 1999.
 = 1300o C, forming
the semirigid oceanic
lithosphere. As it moves over the horizontal section of the
convection cell, the lithosphere cools still more and grows
thicker. In the descending section of the convection cell,
the immersed lithosphere stays semirigid for a long time,
until it gets heated to a temperature of
T
= 1300o C, forming
the semirigid oceanic
lithosphere. As it moves over the horizontal section of the
convection cell, the lithosphere cools still more and grows
thicker. In the descending section of the convection cell,
the immersed lithosphere stays semirigid for a long time,
until it gets heated to a temperature of
T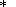 . Thus, the
oceanic lithosphere does not float on the surface of the
underlying portion of the mantle, but takes part in the
convective circulation of the mantle material in the entire
mantle cell and comprises that portion of the mantle which
at a given instant is at a temperature below
T
. Thus, the
oceanic lithosphere does not float on the surface of the
underlying portion of the mantle, but takes part in the
convective circulation of the mantle material in the entire
mantle cell and comprises that portion of the mantle which
at a given instant is at a temperature below
T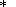 . The
horizontal size of convection cells being no more than 20
thousand kilometers and the maximum mantle convection flow
velocity, of the order of 10 centimeters per year, the age
of the oceanic lithosphere cannot exceed 200 million years.
. The
horizontal size of convection cells being no more than 20
thousand kilometers and the maximum mantle convection flow
velocity, of the order of 10 centimeters per year, the age
of the oceanic lithosphere cannot exceed 200 million years.
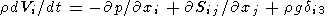
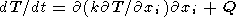
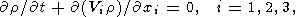
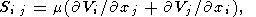
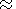 10-23 with respect to the terms on the
right-hand sides of the
equations, and so these inertial terms can be disregarded.
In the Boussinesq approximation, we put
r = r0(1
- aT) in the last buoyancy term of equation
(1) and
r = r0
in all the remaining terms of equations
(1)-(3). We will reckon pressure from its hydrostatic
distribution
p(z) subject to the condition
10-23 with respect to the terms on the
right-hand sides of the
equations, and so these inertial terms can be disregarded.
In the Boussinesq approximation, we put
r = r0(1
- aT) in the last buoyancy term of equation
(1) and
r = r0
in all the remaining terms of equations
(1)-(3). We will reckon pressure from its hydrostatic
distribution
p(z) subject to the condition
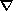 p0 = -r0g.
We introduce dimensionless
variables, taking the mantle thickness
D as a unit of
measurement for length,
D/k for velocity,
D2/k for
time,
T0 for temperature,
m0 for viscosity,
m0 k/D2 for
pressure and stress, and
kT0/D2 for
heat source density.
p0 = -r0g.
We introduce dimensionless
variables, taking the mantle thickness
D as a unit of
measurement for length,
D/k for velocity,
D2/k for
time,
T0 for temperature,
m0 for viscosity,
m0 k/D2 for
pressure and stress, and
kT0/D2 for
heat source density.
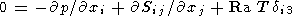
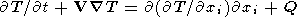
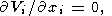
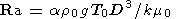
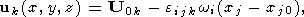
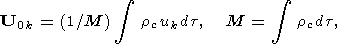
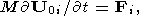
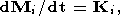
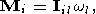
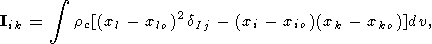
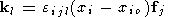
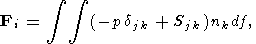
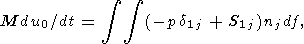
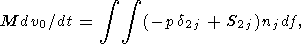
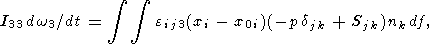
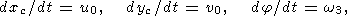
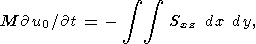
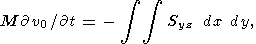
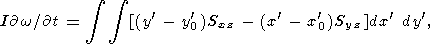
 passing through its center
of gravity and
calculated in the moving coordinate system with the axes
x
passing through its center
of gravity and
calculated in the moving coordinate system with the axes
x